算法_python_学习记录_02

算法学习和视频学习过程中，有许多前几天还不知道的知识点，现在一点一点归纳整理出来，稳步前进，前进~

20_贪心算法系列题

00_参考文档

1. 详解贪心算法（Python实现贪心算法典型例题）_顺序贪婪算法-CSDN博客
2. Python算法L5：贪心算法_python 贪心算法-CSDN博客

01_分数背包(洛谷P2240)

降序排序 + 循环中分支语句（部分拿取也是循环结束）

分数背包是典型的贪心算法问题，基本的思路就是先排序，然后从价值最高的向下拿；然后能全拿走的全拿走，不能全拿走的获取背包剩余的容量部分

li1 = [(10,60),(15,45),(20,100),(30,120)]  def getMaxValue_by_weight(li, w_remain):li.sort(key = lambda x: x[1]/x[0], reverse=True)total_v = 0i = 0while w_remain > 0:wi = li[i][0]      # 重量vi = li[i][0]      # 价值pcs_val = vi/ wi   # 单位价值if w_remain > wi： # 全拿走total_v += viw_remain -= wielse:              # 拿部分faction1 = w_remain / witotal_v += pcs_val * w_remainw_remain = 0i += 1return total_vprint(getMaxValue_by_weight(li1,50))
--------------
240.0

02_移除K个数字(Leetcode402)

见参考文档1，贪心+ 栈

贪心算法，但这次的思路并不是先排序，因为要求是移除K个数字，但原来的次序并没有变化，否则就不是1219而是1129了；要让数字最小，把最小的放在最高位上，然后依次把第二小的放在第2高位上，以此类推；本题的步骤，主步骤是按顺序从左开始把数字压栈，然后向后看数字是不是比它小，则把原数弹栈，把当前数压栈；执行K次后或数字全部遍历后退出。

def remove_k_number(s):nums1 = list(map(int,s))s = []    # 栈for i in range(len(nums1)):number = int(nums1[i])while len(s)!=0 and s[len(s)-1]>number and k>0: # 栈里的数比较大s.pop(-1)k -= 1if number != 0 or len(s)!=0:s.append(number)while len(s)!=0 and k>0:s.pop(-1)k -= 1ret = ''.join(str(i) for i in s)return ret

03_排队接水 (洛谷P1223)

10 
56 12 1 99 1000 234 33 55 99 812

排序后计算即可，这里有个小知识点，就是输出原list中元素的索引号（idx+1），开始用字典做发现不对，因为可能有同值的，在字典里就会被后面的idx覆盖掉，所以尝试用元组

# li = 56 12 1 99 1000 234 33 55 99 812
li2 = []
for idx, v in enumerate(li):li2.append((v,idx+1))for x in li2:print(x[1],end=' ')  # 这样就能得到对应的索引了

 另外，还有点小问题是平均等待时间的计算，需要在循环中当前的值*（n-1-i)个后面在等的人，最后sum()计算后再除以总人数n =10

04_小苯的数字权值

小苯的数字权值_牛客题霸_牛客网

这道题涉及2个知识点（质数筛，权值）的混合，任一知识点没掌握到位都完成不了。这道题在牛客练习50题中的第1题，题目没有对权值进行明确的描述，一开始我以为任何一个数字都是2，分解质因子数进行count然后乘以2就行了。但实际上除了示例能完成，通过率是0%。

权值涉及到求某个数的因子数量，例如12的因子是1，2，3，4，6，12共6个，而它的质因数是2，2，3 三个，恰好有个公式通过质因数计数来计算它的因子数，它就是

  

以12为例，质因数2有2个，3有1个，我们可记为[（2，2）（3，1）]，所以，（2+1）*（1+1）=6

最后还要max()来获取最大值。

求某个数的因子数量

1. 暴力遍历（清晰易懂） - 从1到sqrt(n)的所有整数i，能整除n则统计

2. 质因数分解（高效），然后用K = (a1+1)*(a2+1)*...的计算方式得到

在通义上问AI，得到的while循环，i=1,2,3，然后i+=2，即跳过了2以外的偶数，会更高效些，但初次接触时，还是用比较易懂的代码来理解

def count_factors(n):if n <= 0:return 0if n == 1:return 1  # 1 只有自己一个因子count = 1  # 最终因子个数temp = nfor i in range(2, int(n**0.5) + 1):exponent = 0while temp % i == 0:temp //= iexponent += 1if exponent > 0:count *= (exponent + 1)# 如果最后剩下的数是一个大于1的质数if temp > 1:count *= 2  # 它的指数是1，所以 (1+1)=2return count

05_所有子序列权值和

小红的子序列权值和_牛客题霸_牛客网

这道题权值的情况思路是一样的，关键的前提是子序列的所有非空子序列，求解有2进制方法，递归，DFS等，前面某道题好像刚接触过，但又想不起来了，还跟前面左右括号的递归混在一起有点乱，所以我们先放在这里，后面讨论过其他算法后再回过头来看。

所有子序列问题

见22_子串与所有子序列

21_动态规划算法系列

21_00_参考文档

• 动态规划_百度百科
• 一文搞懂动态规划：从入门到精通-CSDN博客 一文搞懂动态规划：从入门到精通
• https://zhuanlan.zhihu.com/p/18581020726 什么是动态规划，动态规划的好处
• https://zhuanlan.zhihu.com/p/704095109 计算机界的“魔法”：深入浅出理解动态规划
• https://juejin.cn/post/7410728037418532874 动态规划算法详解（附代码实现）

21_01_文档学习笔记

动态规划（Dynamic Programming，DP）是运筹学的一个分支，是求解决策过程最优化的过程。20世纪50年代初，美国数学家贝尔曼（R.Bellman）等人在研究多阶段决策过程的优化问题时，提出了著名的最优化原理，从而创立了动态规划。

动态规划的应用极其广泛，包括工程技术、经济、工业生产、军事以及自动化控制等领域，并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果。

例如最短路线、库存管理、资源分配、设备更新、排序、装载等问题，用动态规划方法求解更为方便

动态规划的概念最早由美国数学家理查德·贝尔曼在上世纪50年代提出，起初是为了优化复杂的军事决策问题。简而言之，动态规划是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

它利用一个表（通常称为DP表）存储子问题的解，避免重复计算，从而达到高效解决问题的目的。

其核心思想可以用一句话概括：“如果一个问题可以被分解成多个重叠子问题，则解决这个大问题的最佳方法就是记住之前解决过的子问题的答案。”

21_02_概念引入

• 可将过程分成若干个互相联系的阶段，在每一阶段都需要作出决策，从而使整个过程达到最好的活动效果

• 各个阶段决策的选取不能任意确定，它依赖于当前面临的状态，又影响以后的发展

• 当各个阶段决策确定后，就组成一个决策序列

• 这种把一个问题看作是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程

• 各个阶段采取的决策，一般来说是与时间有关的

• 一个决策序列就是在变化的状态中产生出来的，故有“动态”的含义

21_03_基本思想

在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。

动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题

与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的

若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次

如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间

可以用一个表来记录所有已解的子问题的答案，这就是动态规划法的基本思路

具体的动态规划算法多种多样，但它们具有相同的填表格式

21_04_什么是动态转移方程

在动态规划中，状态转移方程 是算法的核心，它描述了一个问题的解如何通过子问题的解递推而来。换句话说，状态转移方程是动态规划的“递归公式”，它体现了问题的 最优子结构。

21_05_动态规划典型代码

dp01_斐波那契及跳台阶

这段代码优雅地展示了动态规划的核心思路：从最简单的基础情况开始（第1级台阶和第2级台阶），逐步构建到更复杂的层级。每到达新的一级台阶，我们只需简单地查看前两级台阶的上法数并相加，便得到了当前台阶的所有可能上法。这便是动态规划中的“状态转移方程”，即递推公式。

def climbStairs(n):if n == 1:return 1elif n == 2:return 2dp = [0] * (n + 1)      # 创建表格dp[1], dp[2] = 1, 2      # 表格开始部分赋值for i in range(3, n + 1):dp[i] = dp[i - 1] + dp[i - 2]   # 表格随i赋值return dp[n]print(climbStairs(5))  # 输出：8

dp02_01背包

在动态规划的世界里，正确理解和定义状态空间以及边界条件至关重要。以“背包问题”为例，假设你是一名寻宝者，有一个容量为W的背包，面前有n件物品，每件物品都有自己的重量w[i]和价值v[i]，你的任务是选择一些物品装入背包，使得总价值最大，但总重量不超过背包容量。

这个问题的状态可以定义为dp[i][w]，表示考虑前i件物品时，背包容量为w时的最大价值。边界条件则是dp[0][w]=0（没有物品可选时价值为0），dp[i][0]=0（背包容量为0时无法装入任何物品）。

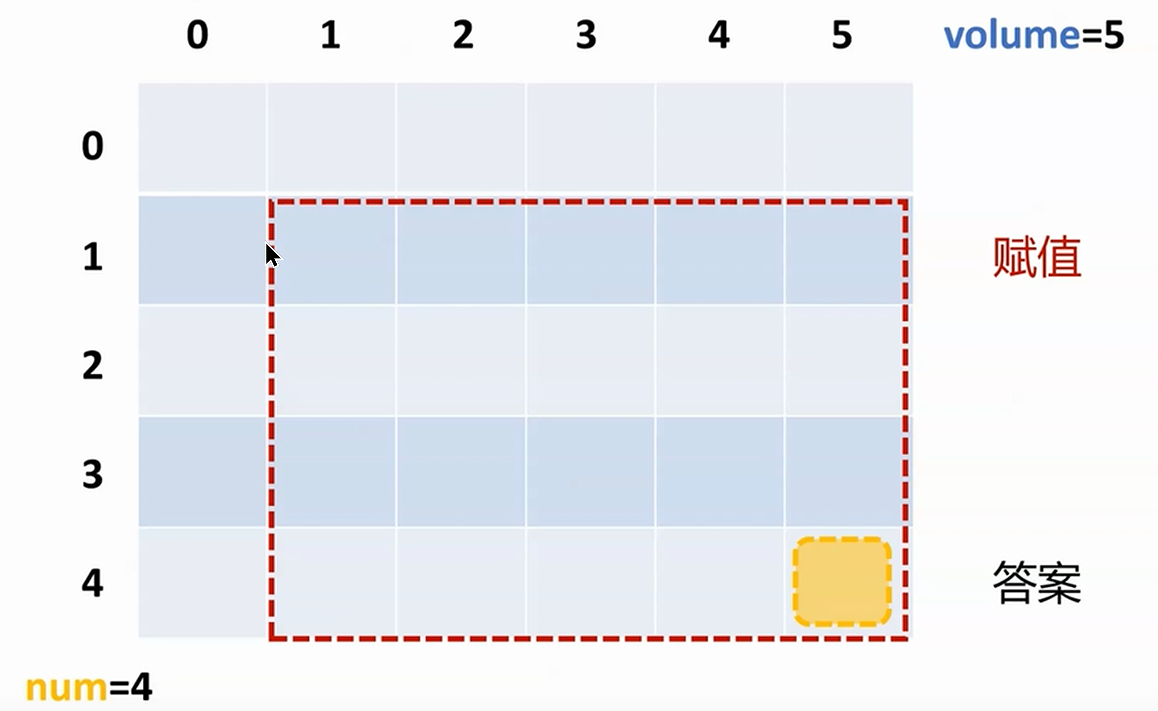
def knapsack(W, wt, val, n):dp = [[0 for w in range(W + 1)] for i in range(n + 1)]# 构建状态表for i in range(1, n + 1):for w in range(1, W + 1):if wt[i-1] <= w:dp[i][w] = max(dp[i-1][w], dp[i-1][w-wt[i-1]] + val[i-1])else:dp[i][w] = dp[i-1][w]return dp[n][W]val = [60, 100, 120]
wt = [10, 20, 30]
W = 50
n = len(val)
print(knapsack(W, wt, val, n))  # 输出：220

dp03_最大子数组和

题目：53. 最大子数组和 - 力扣（LeetCode）

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

def maxSubArray(nums):maxSum = nums[0]; currSum = nums[0]for i in range(1, len(nums)):currSum = max(currSum+nums[i],nums[i])maxSum = max(maxSum, currSum)return maxSumnums = [-2,1,-3,4,-1,2,1,-5,4]

但这种写法对于初学DP的人就有点对不上，需要把dp[ i ]添加上才能看出来，完成代码后再回过来看，其实这是一个很典型的动态规划示例，我们取[0]位上的数值，然后按次序进行和运算，

• 如果此次获取的值nums[i] 比 前面累加值+nums[i]还要大（前面累加值为负），则填上当前值，自然分割完成！

• 否则（前面累加为正），填上累加值，不进行分割

def maxSubArray(nums):n = len(nums)dp = [0] * n          # dp[i]：以 nums[i] 结尾的最大子数组和dp[0] = nums[0]maxSum = dp[0]        # 全局最大值for i in range(1, n):dp[i] = max(dp[i-1] + nums[i], nums[i])  # 状态转移maxSum = max(maxSum, dp[i])# 把每一步的 dp 表打出来print("dp 表内容：", dp)return maxSum# 测试
nums = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
print("最大子数组和：", maxSubArray(nums))# ------------------
# dp 表内容： [-2, 1, -2, 4, 3, 5, 6, 1, 5]
# 最大子数组和： 6

稍微进阶一下，除了最大值外，还需要获取构成最大子数组的元素

由于要获取元素，就要记录开始的下标和结束的下标

def maxSubArray(nums):n = len(nums)dp = [0] * n          # dp[i]：以 nums[i] 结尾的最大子数组和start = [0] * n       # start[i]：以 i 结尾的子数组的起始下标dp[0] = nums[0] ;  start[0] = 0maxSum = dp[0];  max_end_idx = 0       # 记录全局最大值及对应的结束下标for i in range(1, n):# 状态转移if dp[i-1] + nums[i] > nums[i]:dp[i] = dp[i-1] + nums[i]start[i] = start[i-1]      # 延续上一段else:dp[i] = nums[i]start[i] = i               # 从当前位置重新开始if dp[i] > maxSum:          # 更新全局最大值maxSum = dp[i]max_end_idx = i# 根据 start 与 max_end_idx 回溯得到子数组left = start[max_end_idx]sub = nums[left:max_end_idx + 1]# 打印结果print("dp 表内容：", dp)print("最大子数组和：", maxSum)print("构成子数组的元素：", sub)return maxSum
# 测试
nums = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
maxSubArray(nums)

dp04_最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

def lengthOfLIS(nums):n = len(nums)dp = [1]*nmaxLen = 1for i in range(1,n):for j in range(0,i):if nums[j] < nums[i]:dp[i] = max(dp[i],dp[j]+1)maxLen = max(maxLen, dp[i])return maxLen

dp05_最长公共子序列

题目描述：给定两个字符串，求它们的最长公共子序列长度。

思路：最长公共子序列问题是典型的二维动态规划问题。

def long_common(li1, li2):m = len(li1)n = len(li2)dp = [[0 for j in range(n+1)]for i in range(m+1)]for i in range(1,m+1):for j in range(1,n+1):if li1[i-1] == li2[j-1]:dp[i][j] = dp[i-1][j-1]+1else:dp[i][j] = max(dp[i-1][j], dp[i][j-1])return dp[m][n]
#------------------
li1 = 'AEBDDC'
li2 = 'FECDC'
print(long_common(li1,li2))

dp06_找零钱问题

给定不同面值的硬币和一个总金额，计算有多少种组合可以凑成这个金额

def getChange(amount, li):dp = [0]* (amount+1)dp[0] = 1for coin in li:for j in range(coin, amount+1):dp[j] += dp[j-coin]print(dp)return dp[amount]
li = [1,2,5,10,50,100]
print(getChange(25,li))
#-----------------
#[1, 1, 2, 2, 3, 4, 5, 6, 7, 8, 11, 12, 15, 16,19, 22, 25, 28, 31, 34,40, 43, 49, 52, 58, 64]

dp07_割钢条

给定价格表 p，其中 p[i] 表示长度为 i 的钢条可卖的价格（p[0] 无意义，可设为 0）。求把一根长度为 n 的钢条切成若干段后，总售价的最大值；同时输出最优切割方案。

• 状态：dp[i] 表示长度为 i 的钢条能获得的最大收益。

• 转移：枚举第一次切出的第一段长度 j（1 ≤ j ≤ i），得到

  dp[i] = max{p[j] + dp[i-j]} ，对所有 j。

def cut_rod(p, n):# dp[i]：长度为 i 的最大收益dp = [0] * (n + 1)# cut[i]：让 dp[i] 取得最大收益时的第一段长度cut = [0] * (n + 1)# 自底向上填表for i in range(1, n + 1):max_val = -1best_j = 0for j in range(1, i + 1):if p[j] + dp[i - j] > max_val:max_val = p[j] + dp[i - j]best_j = jdp[i] = max_valcut[i] = best_j# ------------ 打印过程 ------------print('dp 表（长度 -> 最大收益）：')for i in range(n + 1):print(f'len={i:2d}, value={dp[i]:3d}, first_cut_len={cut[i]}')# ------------ 回溯最优方案 ----------pieces = []remain = nwhile remain > 0:pieces.append(cut[remain])remain -= cut[remain]print(f'\n最优切割方案：{pieces}（总长 {n} = {"+".join(map(str, pieces))}）')print(f'最大收益：{dp[n]}')return dp[n], pieces# ----------------- 示例 -----------------
if __name__ == '__main__':# 下标 0 不用；下标 i 对应长度 i 的售价p = [0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]n = 8cut_rod(p, n)

22_子串与数组中所有子序列

子串与子集是看着相似实则有很大差别的两个问题，子串最大的特点是不能跳过中间的字符，而子集可以跳过中间的元素。

A_所有子串的获取

对于子串，据AI说没有太好的方法，一般只能使用双重循环来获取，不过可以有两条路径来获取，第1条是按开始位置，比如‘abcd’，外层循环控制的就是从'a'，'b'，'c'，'d'开始；另一条是按长度，这时的外层循环控制的是字符的长度从1开始，2字符，3字符，4字符。

按开始位置

def all_substring_1(s):arr = []n = len(s)for i in range(n):for j in range(i+1, n+1):arr.append(s[i:j]return arrall_substring_1('abcde')
----------
['a', 'ab', 'abc', 'abcd', 'abcde', 'b', 'bc', 'bcd','bcde', 'c', 'cd', 'cde', 'd', 'de', 'e']

按长度

def all_substring_len(s):arr = []n = len(s)for i in range(1, n+1):    # 例3个字符len()=3,[1,3)取不到第3个字符for j in range(1, n+1-i):arr.append(s[j:j+i]return arr
all_substring_len('abcde')
-------------------------
['a', 'b', 'c', 'd', 'e', 'ab', 'bc', 'cd', 'de', 'abc', 'bcd', 'cde', 'abcd', 'bcde', 'abcde']

A1_好串的获取

典型的'red'串的获取

题目：小红拿到了一个只包含'r','e','d'三种字母的字符串，有多少子串满足三种字母的数量严格相等？ 例输入 redrde 输出 4 （【red】rde, r[edr]de, red[rde],[redrde])

一开始，没有看懂题目，以为是三个字符的滑动窗口，然后判断red三个字符是否存在，使用了python的zip结构，但忽略了6个字符，9个字符，3n字符仍然成立的情况，我们先做一下只考虑3字符的情况：

def get_red_only3_char(s):li1 = list(s)li2 = li1[1:]li3 = li1[2:]zipped = zip(li1,li2,li3)chk = ['r','e','d']icnt = 0for idx, a in enumerate(zipped):if sorted(list(a)) == sorted(chk):icnt += 1return icnt

但这样肯定是不行的，通过率只有9.09%。于是我们换种思路，所有子串只要red三个字符出现的次数相等，所以3，6，9......3n的都可以，很明显可以用字符长度进行，并且只处理3的倍数的子串。

def all_substring_3n(s):arr = []n = len(s)icnt = 0for i in range(3, n+1,3):for j in range(0, n+1-i):# arr.append(s[j:j+i])x = s[j:j+i]if check_good_red(x):icnt += 1return icntdef check_good_red(s):n2 = len(s)d_goal = {'r':n2//3, 'e':n2//3, 'd':n2//3}d = {}for ch in s:d[ch] = d.get(ch,0)+1if d == d_goal:return 1else:return 0print(all_substring_3n(s))

这个程序用例通过率为18.18%，运行超时！请检查是否循环有错或算法复杂度过大。

根据上面的方法，我们暂时无法通过，于是我们先看一下其他的题目。

再完成下面3个题目后，我们再回来用双指针的方式进行解题：

def count_all_windows(s):n = len(s)result = 0for w_size in range(3, n+1, 3):d = {}for i in range(w_size):   # 先初始化一个窗口，例如 [red],在长度6里是[redrde]ch = s[i]d[ch] = d.get(ch,0)+1if len(d) == 3 and len(set(d.values())) == 1:   # 如果恰好初始化的窗口就满足条件result += 1for right in range( w_size, n):  # 双指针ch_left = s[right - w_size]   # 3-3 = 0ch_right = s[right]# 添加右边字符计数d[ch_right] = d.get(ch_right, 0)+ 1# 滑动窗口左指针不需要计算d[ch_left] -= 1if d[ch_left] == 0:del d[ch_left]# 每移动一下判断一次if len(d) == 3 and len(set(d.values())) == 1:result += 1return result

这次的通过率是36.36% ，算是在前面的基础上又翻了一倍，但依然运行超时，但是到这里我已经黔驴技穷了，就先这样吧。

A2_最长不重复子串

最长不含重复字符的子字符串_牛客题霸_牛客网

请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。

数据范围:  s.length≤40000 

输入："abcabcbb"  

返回值：3

说明：因为无重复字符的最长子串是"abc"，所以其长度为 3。

这道题跟上面的好串有些类似，假如我仍以先获取全部的子串，再检查每个子串里是否有重复的字符，虽然效率低以及运行会超时，总是能计算得到的。但这肯定不是这类题目的考点。

看了题解（上面题目链接有题解），这类问题需要使用到双指针以及哈希表(字典），开始时左、右指针都从0下标开始，先右指针右移，用字典记录字符出现次数，判断每一步icnt与右指针减左指针+1的最大值；当发现出现重复字符时，左指针字符从字典中减1个计数，并右移，每一步判断右指针字符是否字典中计数仍大于1，如果不大于1，则左指标停下, 继续下一轮循环。

由于这里的右指针每一轮都会+=1操作且不需要中间改变值，因此也可以用for 循环

    def lengthOfLongestSubstring(self , s: str) -> int:# write code heredic1 = {}icnt =0left = 0; right = 0for right in range(len(s)):ch = s[right]dic1[ch] = dic1.get(ch,0)+1while dic1[ch] >1:dic1[s[left]] -=1left += 1icnt = max(icnt, right-left +1)return icnt 

A3_最小覆盖子串

最小覆盖子串_牛客题霸_牛客网

给出两个字符串 s 和 t，要求在 s 中找出最短的包含 t 中所有字符的连续子串。

输入："XDOYEZODEYXNZ","XYZ"

返回值："YXNZ"

这道题与上面一题非常像，但又更进阶了一步，前面是1个字符串，而这里给出2个字符串，简单的思路那就需要两个哈希表(字典)来解决问题。

而且这道题里有个坑，就是字符串t可能是相同字符，例如“AA”，所以在字典的计数上就不能跟上面直接dic1[s[left]] -= 1这样的操作了，我们需要额外再写一个check_dic_enough(d1,d2)的函数来判断是否满足t字符串的基本条件。

本质上还是双指针，且右指针每一轮+=1并不会中途更改，所以右指针用for 循环来控制，减少循环最后right+=1的代码步骤。

def check_dic_enough(d1,dtgt):for x in dtgt:if d1[x] < dtgt[x]:return Falsereturn Truedef minWindow(S,T):li = []d1 = {}dtgt = {}for ch in T:  # 先把target目标的字典完成dtgt[ch] = dtgt.get(ch,0)+1d1[ch] = d1.get(ch,0)         # 同时把d1也初始化，防止报错left = 0for right in range(len(S)):ch = S[right]if ch in dtgt:d1[ch] = d1.get(ch,0)+1    # while check_dic_enough(d1,dtgt):ch_del = S[left]if ch_del in T:   # target字典中有计数的才减掉d1[ch_del] -= 1left += 1sout = S[left-1:right+1]b_append = Truefor ch in T:if ch not in sout:b_append = Falsebreakif b_append:li.append(sout)# li中取最小长度的字符串ilen_min = len(li[0])idx_min = 0for idx, ss in enumerate(li):if len(ss) < ilen_min:ilen_min = len(ss)idx_min = idxreturn li[idx_min]

上面代码可以通过15/20组用例，出错的分别是

• "a","aa" ，应该输出“”
• "a","b" ， 应该输出“”
• "ab","A"， 应该输出“”

用print()打印一下过程，发现后面没有考虑S比T字符少的情况，以及当最后li为空的时候，没有输出“”，因此添加几句

if len(S)<len(T) :return ""if len(li) == 0:return ""

A4_包含不超过2种字符的最长子串

做了上面最长和最小，再做一道不超过2种字符的，

包含不超过两种字符的最长子串_牛客题霸_牛客网

给定一个长度为 n 的字符串，找出最多包含两种字符的最长子串 t ，返回这个最长的长度。

输入：nooooow  输出：6

此类题目的起手式基本都一致，只是在过程中有些不同，对于几种字符，可以用len(dic1)来获得，而当dic1中的某个字符计数为0时，删除它 del d[c]。另外求最长而不用输出字符串时，直接用max(res, right-left+1)就可以了。

left = 0
d = {}
res = 0for right in range(len(s)):ch = s[right]d[ch] = d.get(ch,0)+1# print(d, len(d))   # {'n': 1, 'o': 1, 'w': 1, 'c': 1} 4while len(d) >2 and right<= len(s):c = s[left]d[c] -= 1if d[c] == 0:del d[c]left += 1res = max (res, right-left+1)print(res)

B_所有子序列的获取

B1_python常见的几种方式

第一种，itertools

在python的标准库中，“人生苦短，我用python”，python标准库已经提供了很多实用的内置函数。但仍然是太容易得到的函数就不珍惜，也没有兴趣去研究它的实现方式，也就不能继承和发扬，把它的思路应用到其他的地方，这对于学习算法是没有好处的。

from itertools import combinationsli = []
for r in range(0,len(arr)+1):print(list(combinations(arr,r)))  # 打印出来是元组形式 [(1,), (2,), (3,)]obj = combinations(arr,r)             # 如下打印出list的形式li_tmp = [list(comb) for comb in obj]li.extend(li_tmp)
li
--------------------
[()]
[(1,), (2,), (3,)]
[(1, 2), (1, 3), (2, 3)]
[(1, 2, 3)][[], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3]]

在itertools中，combinations就是组合操作，permutations就是排列操作，我们在学校中曾经学过的排列、组合的公式就可以用它们快速实现，下面是排列与组合从n项中取r项会产生的不同的排列或组合的次数，可以看到排列可调换前后次序，其次数会比组合（不调换次序）要多。

而我们求所有子序列的情况就相当于是求组合，只不过要从C(n,1),C(n,2)...一直求到C(n,n)

 

P(5,2) = 5!/ (5-2)! = 5*4*3*2*1 / 3*2*1 = 5*4 = 20

C(5,2) = 5!/ (2!* 3!) = 5*4*3*2*1 / 2*1 * 3*2*1 = 20/2 = 10

继续说Combinations，当我们求C(3,2)时，直接就用"combinations(arr,2)"即可

arr = [1,2,3]
c3_2 = combinations(arr,2)
c3_2, type(c3_2)
---------------------
(<itertools.combinations at 0x148e2d5bd80>, itertools.combinations)

只不过得到的是tiertools.combinations的对象，还需要用for in把它们显示出来: 

for x in c3_2:print(x, end=',')-----------------
(1, 2),(1, 3),(2, 3),

我们看到这里是元组，如果需要列表，还需要进行转换

for x in c3_2:x2 = list(x)print(x2, end=',')
-------------
[1, 2],[1, 3],[2, 3],

然后我们使用python列表推导的方式，快速得到其列表形式

list_C32 = [list(x) for x in combinations(arr,2)]
list_C32
------------------
[[1, 2], [1, 3], [2, 3]]

itertools标准库不需要额外安装，直接可以使用，这给我们带来了很大的便捷，我们只需要在外层加一层循环，把组合从C31,C32,C33分别求出来，用list.extend(list2)的方式连在一起就OK了。 

第二种，二进制枚举法（位运算）

如上所说，使用itertools十分便捷，但用了它就没有任何进步的空间了，如果自己搞不定还怎么进步！所以在学习算法的路径上，我们必须学会其他的算法自己把它们搞出来，这些就像是乐高玩具的一些基础模组，还可以跟其他模组之间排列、组合成新型的中型模组~

所有子序列，恰好可以用二进制枚举法来做，而总共的次数就是2^n；

0	000	[,,]
1	001	[,,1]
2	010	[,2,]
3	011	[,2,1]
4	100	[3,,]
5	101	[3,,1]
6	110	[3,2,]
7	111	[3,2,1]

从上表可知，只要我们由range(0,8)进行循环（外层），然后在每次循环中把i（例如3）分别跟第0位，第1位和第2位“与”操作，就能获取到这一次的子序列内容，把这些子序列都append到results的总列表中，最后就得到了所有子序列。

def sub_bitmask(arr):n = len(arr)total = 1<<nprint('n',n,'  total',total)results = []for mask in range(total):    # 2^n种组合，恰好对应2进制的十进制数值，当前8subseq=[]for i in range(n):      # 每一次(8次)，分别检查0，1，2位上是否为1if mask & (1<<i) :subseq.append(arr[i])results.append(subseq)return resultssub_bitmask(arr)
---------------------------
n 3   total 8
[[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]

这种二进制枚举的方式，我觉得是非常朴素的算法，没有一丝取巧的成分在，规规矩矩由0000二进制变换到1111，不能跳过任何一步，是比较容易理解和快速进行应用的。但在时间复杂度上，好像是2^n的外层循环乘上n的内层循环，AI给出的性能当n=20时，会进行20,971,520次计算，适用场景在n<20，也就是说竞赛或考试中有部分测试数据会超时的。

二进制位运算拓展

由于用到了位运算，让我又想起一道题，统计整数二进制数中1的个数，这道题如果用python有很多取巧的方式，比如说转二进制字符串bin(n)，再使用.count('1')，就可以得到，这么做没问题，但同时你也就错过了一个经典算法（Brian Kernighan’s Algorithm）。

def count_bin_one(n):ret = bin(n).count('1')print(bin(n))return retcount_bin_one(13)
--------------------
0b1101
3

我们再用这个算法来看一下

# Brian Kernighan’s Algorithm
def count_ones_optimized(n):cnt = 0while n:print(bin(n),'before n', n)print(bin(n-1),'before n-1',n-1)n &= (n-1)cnt += 1print(bin(n),'after n', '  cnt=',cnt)count_ones_optimized(13)
---------------------
0b1101 before n 13
0b1100 before n-1 12
0b1100 after n   cnt= 1    # 去掉最低位的10b1100 before n 12
0b1011 before n-1 11
0b1000 after n   cnt= 2    # 去掉最低位的10b1000 before n 8
0b111 before n-1 7
0b0 after n   cnt= 3       # 去掉最低位的1

这里我们又学到一些知识点，但仍要知道这个优化的算法是相对于哪一个朴素直观容易理解的算法来的，我们再看一下最朴素的，这里的32就是一个魔数，另外必须完成32次循环。

# 用每一位与操作的方法
def count_ones_basic(n):cnt = 0for i in range(32):   # 32位整数if n>>i & 1 == 1: # 1右移i位cnt+=1print(n>>i, bin(n>>i),'右移%d位'%i,' icnt',cnt)return cnt
count_ones_basic(13)
------------------------
13 0b1101 右移0位  icnt 1
3 0b11 右移2位  icnt 2
1 0b1 右移3位  icnt 33

第三种，递归

前面的二进制位运算，通过十进制的特性，给子序列的获取提供了一根坐标轴，能确保不会产生遗漏，接着我们再来看下递归的方式。

我觉得递归的方式都要从0开始，先计算1，2，3，4次，才能通过它的特点，推导出解析式。

• 0. 【】空集，返回空集 一个
• 1. 【1】，只有一个非空，返回【】，【1】共二个
• 2. 【1，2】，有二个，返回【】，【1】，【1，2】，【2】 共四个
• 3. 【1，2，3】，有三个，返回【】，【1】，【1，2】，【1，2，3】，【1，3】，【2】，【2，3】，【3】共八个

前面已经知道了子序列的个数是2^n ，当n=3时共有8个，那么按照刚才的推导，n=4时，会在n=3的8个的基础上，再把【4】添加到原来的8个中形成新的8个。这里很奇怪，我已经把迭代的情况推导出来了，但我还是没有搞清楚递归的具体实现情况。但是我们学递归的时候就老老实实用递归，不要好高骛远什么都想要，而且必须把递归弄踏实了，再说迭代的事。

单通道递归

递归就像是套娃，打开来以后下一个娃娃还是一模一样的，但总要有个尽头。

递归又像是《盗梦空间》，进入一层梦境后，在某处进入二层梦境完成任务后还需要返回一层梦境的坐标，继续后续一层梦境的任务。

递归在我们日常生活中遇到比较频繁的就是文件夹遍历了，我们有时候把某个学习文件藏到很深的目录下面，还可能创建几个空文件夹作为分支，那么递归就是不断的点击文件夹进入下一层，如果找到文件就返回，如果还有文件夹就继续进。

我们再把文件夹想像成一间房间，进到这间房间后可能房间里有东西，但只有一扇门；进到下一间房间也是这样，那么我们认为它是一个单通道递归。递归除了递进外，还需要归来，这个可以想像成每间房间里都有一个密码柜，但密码在下一层的房间里，只有走到尽头的房间没有密码柜，并且有倒数第二间的密码柜的密码，所以还必须一间一间拿到密码返回上一间，输入密码获取再上一层的密码，再返回上一层，再输入密码....直到回到第一间房间，打开密码柜后获取宝物。

单通道递归是简单的，理解起来也没有太多阻碍，比如数的阶乘计算，n! = n(n-1)...1；每下一层只有一个门，一直下到最底层获取到常数1开始返回，返回时操作

def factorial(n):"""递归计算阶乘"""if n == 0 or n == 1:  # 基线条件：0! 和 1! 均为 1return 1else:return n * factorial(n - 1)  # 递归调用自身factorial(5)
---------------
120

上面是典型代码，代码写得很精炼，但对于初学者非常不友好，它把返回上一层后的其他操作跟返回的动作绑定在了一起，但实际过程中很多操作是分开的，比如拿到1后回到倒数第二层，此时的操作 n* factorial(n-1) ,n已经在进下一层的时候操作完成了(这里是2)，一直在等factorial（n-1)的返回值（这里是1），得到结果 2*1 = 2，然后拿着2返回上一层（倒数第三层）。这个其实很重要，因为调用 factorial(n-1)之前的操作都是递进前的操作/准备工作，而fractorial()是递进操作自身，而fractorial()之后的操作是返回上一层之间的扫尾工作，最后return 才是归的操作，只是由于这个程序里前置，扫尾的步骤太少因此代码可以这样写，按照实际的情况写成如下形式或许对整个过程有更好的理解：

# 数的阶乘
def factorial(n):"""递归计算阶乘"""if n == 0 or n == 1:  # 基线条件：0! 和 1! 均为 1print('enter n:',n)return 1else:print('enter n:',n)fnext = factorial(n - 1)ret = n*fnextprint('back to n:',n, ' ret=',ret)return ret
factorial(5)
-----------------
enter n: 5
enter n: 4
enter n: 3
enter n: 2
enter n: 1
back to n: 2  ret= 2
back to n: 3  ret= 6
back to n: 4  ret= 24
back to n: 5  ret= 120

双通道递归

我们都知道进入山洞寻宝，绝对不可能只有一条通道，每个叉路口可能会有几个通道，比如八门金锁阵，每一次都会"生，死，惊，开，杜，景，休，伤" 八门一起呈现在你面前；不过一上来就是八门太难理解了，我们还是降低点难度，用每个叉口都有左、右两条路。这个看起来似乎又跟二叉树的结构有些联系起来。

双通道递归的典型示例就是前面学过的进阶排序中的快速排序和归并排序这两个。它们两个很相似，主要是在递归的通道上，都是分成两部分，先递归左边，再递归右边。但在前置操作，扫尾操作上是有比较大区别的。

快速排序是先进行比较多的前置操作，用partition函数完成了当前项的归位操作，然后递归左边部分，等左边部分返回后，再递归右边部分，等右边也返回后，再回到上一层的左边部分.....

而归并排序是先进行二分操作，然后递归左边部分，等左边返回再递归右边部分，等右边返回，再进行Merge函数扫尾操作完成这个部分的排序，然后再返回上一层。

所以，快速排序的partition函数在前置操作上，而归并排序的merge函数在扫尾操作上，这是它们之间最大的差别。

另外，归并的二分是平分，所以递归的深度是一定的，其平均水平与最差情况不会有太多差别，但快速排序需要看运气，如果每一层partition都分成 1，n-i-1的情况，它的效率就低到选择排序的水平。

多通道递归

回到所有子序列这个问题上来，它肯定不是单通道递归，也不是双通道递归，我们看得出它的通道数量k是可变的，从山洞寻宝的角度来看，就是每次叉路口通道数量不确定。在这个问题上，通道数量每次都要乘2的。

对于这样的情况，就不可能写成递归左，再递归右的形式，于是就免不了使用for in的循环方式来进行多通道的递归。

回溯递归的简单代码

def subsequences_backtracking(arr):def backtrack(start, path):results.append(path[:])  # 保存当前路径for i in range(start, len(arr)):path.append(arr[i])   # 选择当前元素backtrack(i + 1, path)path.pop()           # 撤销选择（回溯）results = []backtrack(0, [])return results# 示例
arr = [1, 2, 3]
print(subsequences_backtracking(arr))
# 输出：[[], [1], [1,2], [1,2,3], [1,3], [2], [2,3], [3]]

回溯递归debug观察

上面的代码，对于初学者而言是难以理解的，所以我们要加一些print的语句进行观察

arr = [1, 2 ,3]
def sub_tracking(arr):def backtrack(start,path):results.append(path[:])print('results = ',results, 'start=',start)for i in range (start, len(arr)):print('i=',i,end=';')path.append(arr[i])print('path.append',path)backtrack(i+1,path)print('start=',start,'i=',i,'before pop path',path)path.pop()print('i=',i, 'after pop path',path)print('return start',start,'to ',start-1)results = []backtrack(0,[])return resultssub_tracking(arr)
-----------------------------
results =  [[]] start= 0
i= 0;path.append [1]
results =  [[], [1]] start= 1
i= 1;path.append [1, 2]
results =  [[], [1], [1, 2]] start= 2
i= 2;path.append [1, 2, 3]
results =  [[], [1], [1, 2], [1, 2, 3]] start= 3
return start 3 to  2
start= 2 i= 2 before pop path [1, 2, 3]
i= 2 after pop path [1, 2]
return start 2 to  1
start= 1 i= 1 before pop path [1, 2]
i= 1 after pop path [1]
i= 2;path.append [1, 3]
results =  [[], [1], [1, 2], [1, 2, 3], [1, 3]] start= 3
return start 3 to  2
start= 1 i= 2 before pop path [1, 3]
i= 2 after pop path [1]
return start 1 to  0
start= 0 i= 0 before pop path [1]
i= 0 after pop path []
i= 1;path.append [2]
results =  [[], [1], [1, 2], [1, 2, 3], [1, 3], [2]] start= 2
i= 2;path.append [2, 3]
results =  [[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3]] start= 3
return start 3 to  2
start= 2 i= 2 before pop path [2, 3]
i= 2 after pop path [2]
return start 2 to  1
start= 0 i= 1 before pop path [2]
i= 1 after pop path []
i= 2;path.append [3]
results =  [[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3]] start= 3
return start 3 to  2
start= 0 i= 2 before pop path [3]
i= 2 after pop path []
return start 0 to  -1

但这样仍然是很难理解对不对？所以我们还是以递归的解析方式，从0开始做1，2的过程；先从arr = [1] 开始，程序从backtrack(0,[])开始，len(arr)=1，会进行一次for循环即递归 backtrack(1,[1])，进入最后一层results.append([1])，返回倒数第二层扫尾path.pop()又把[1]给弹栈了。

results =  [[]] start= 0
i= 0;path.append [1]
results =  [[], [1]] start= 1
return start 1 to  0
start= 0 i= 0 before pop path [1]
i= 0 after pop path []
return start 0 to  -1[[], [1]]

接着看2的过程，arr = [1,2]，看输出的过程可知道最后6行的情况与上面单个元素的一致，也可以推论出如果arr=[1,2,3] 则[2,3]的部分会与arr = [1,2]是一致的。换个思路想一下，其实就是第一重循环会从0，1，2...的位置开始；如果从0开始，会先走完【】【1】【1，2】【1，2，3】再回过来走【1，3】，然后就退化成为【2，3】，走【2】，【2，3】，最后退化为【3】，走【3】完成。

results =  [[]] start= 0
i= 0;path.append [1]
results =  [[], [1]] start= 1
i= 1;path.append [1, 2]
results =  [[], [1], [1, 2]] start= 2
return start 2 to  1
start= 1 i= 1 before pop path [1, 2]
i= 1 after pop path [1]
return start 1 to  0
start= 0 i= 0 before pop path [1]
i= 0 after pop path []i= 1;path.append [2]
results =  [[], [1], [1, 2], [2]] start= 2
return start 2 to  1
start= 0 i= 1 before pop path [2]
i= 1 after pop path []
return start 0 to  -1

第四种，迭代

先打个桩，后面再来说迭代。

B2_降低难度的子序列获取

如果觉得直接获取所有的子序列有些困难，我们再降低点难度，先尝试获取元素个数为2的子序列，这就好像是n个元素取2个的组合。

第一种，双重循环

双重循环是最朴素的实现组合的方式，易理解，不推荐，但初学者需要知道这种方式

def get_length2_subsequences(arr):result = []n = len(arr)# 外层循环：遍历每个元素作为子序列的第一个元素for i in range(n):# 内层循环：遍历当前元素后面的所有元素for j in range(i + 1, n):# 将当前元素和后续元素组成子序列result.append([arr[i], arr[j]])return result

取2个的子序列用2重循环，取3个的子序列会用到3重循环，取4个呢？很明显如果元素个数可变，这种算法就无法实现。

第二种，itertools

python标准库提供的函数能快速解决这个问题，通过变量k就能获取所需要的可变元素个数的子序列，当然外层加个循环就能获取所有子序列了。

from itertools import combinationsdef k_length_subsequences(arr, k):return [list(comb) for comb in combinations(arr, k)]# 示例
arr = [1, 2, 3]
k = 2
print(k_length_subsequences(arr, k))
# 输出：[[1, 2], [1, 3], [2, 3]]

第三种，递归

def sub_back_2(arr,k):def backtrack(start, path):if len(path) == k:                # 与所有子序列有差别的地方，反而是多出一步判断results.append(path[:])
#             return                      # return 好像可以有也可以无？for i in range(start, len(arr)):path.append(arr[i])backtrack(i+1, path)path.pop()results = []backtrack(0,[])return results
sub_back_2(arr,2)
------------------
[[1, 2], [1, 3], [2, 3]]

可以看到与所有子序列递归的逻辑基本一致，反而多出了len(path)== k的判断语句。这样看到回溯递归更适合做全部而非部分。我们再看一下递归的多通道，外层循环是for i in range(start,len(arr)) 也就是每个idx开始都要走一遍，内层的递归会把当前开始索引开始的直到最后一个元素进行递归，也就是全都跟当前的开始项有关（例如【1】，【1，2】，【1，2，3】，【1，3】）。

如果3个元素怎么办？

上面已经说过了，双重循环解决2个元素的，三重循环解决3个元素的，由于不同元素个数最内层的循环语句都不一样，所以无法解决可变数量的情况，因此朴素的多重循环方法用不了，只能使用itertools，递归等方法。

# 当k=3时，我们可以写三重循环
def get_combinations_k3(arr):result = []n = len(arr)for i in range(n):for j in range(i+1, n):for k in range(j+1, n):result.append([arr[i], arr[j], arr[k]])return result# 但是，当k是变量时，我们无法在代码中写出k层循环。因此，我们使用递归或迭代来模拟。

B3_再用迭代获取所有子序列

多通道的递归真的很难理解，这个时候反而迭代还更容易理解一些：

def generate_subsets(arr):subsets = [[]]  # 从空集开始for num in arr:# 创建新子集 = 现有子集 + 当前元素new_subsets = []for subset in subsets:new_subsets.append(subset + [num])# 合并新子集到结果subsets += new_subsetsreturn subsets# 示例
arr = [1, 2, 3]
print(generate_subsets(arr))
# 输出: [[], [1], [2], [1,2], [3], [1,3], [2,3], [1,2,3]]

迭代的debug观察

def generate_subsets2(arr):subsets = [[]]  # 从空集开始for num in arr:print('num=',num)# 创建新子集 = 现有子集 + 当前元素new_subsets = []print('subsets',subsets)for subset in subsets:print('before new_sub=',new_subsets,'  subset=',subset, '  if +[num]=',[num])new_subsets.append(subset + [num])print('After new_sub',new_subsets)# 合并新子集到结果subsets += new_subsetsreturn subsetsgenerate_subsets2(arr)

num= 1
subsets [[]]
before new_sub= []   subset= []   if +[num]= [1]
After new_sub [[1]]
num= 2
subsets [[], [1]]
before new_sub= []   subset= []   if +[num]= [2]
After new_sub [[2]]
before new_sub= [[2]]   subset= [1]   if +[num]= [2]
After new_sub [[2], [1, 2]]
num= 3
subsets [[], [1], [2], [1, 2]]
before new_sub= []   subset= []   if +[num]= [3]
After new_sub [[3]]
before new_sub= [[3]]   subset= [1]   if +[num]= [3]
After new_sub [[3], [1, 3]]
before new_sub= [[3], [1, 3]]   subset= [2]   if +[num]= [3]
After new_sub [[3], [1, 3], [2, 3]]
before new_sub= [[3], [1, 3], [2, 3]]   subset= [1, 2]   if +[num]= [3]
After new_sub [[3], [1, 3], [2, 3], [1, 2, 3]][[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]

迭代与循环，最初的循环都是数字(下标)的循环，后来一些语言出了for in 的循环，但无论哪种，循环的次数基本是一定的；而迭代往往有次叠加起来的感觉，在编程中迭代常指按顺序访问集合中的元素。

从上面的例子中，可以看到迭代会在原有的基础上，一次一次新增，这个例子中，会一直对subsets进行迭代，从原有的空集，每次都会增加新的元素，例如第1次是 【【】,【1】】，那么下一次就是【空 2】【1 2】==> 【】，【1】，【2】，【1，2】；再下一次在4个子序列基本上再生成【空 3】【1，3】【2，3】【1，2，3】就得到了8个子序列

B5_迭代应用拓展(括号匹配）

现在回想起来，遇到？分成左括号和右括号的，应该也是迭代， 初始时比如 (( ，则subsets里就只有(( , 当遇到？进行迭代，成为 【(((, (()】,继续下去。

def generate_brace(s):subsets = [""]for x in s:new_sub = []print('before subsets=',subsets)for subset in subsets:if x=='?':new_sub.append(subset +'(')new_sub.append(subset + ')')else:new_sub.append(subset+x)subsets = new_subprint('----After subsets=',subsets)return subsetss = '((?)??)'
generate_brace(s)

before subsets= ['']
----After subsets= ['(']
before subsets= ['(']
----After subsets= ['((']
before subsets= ['((']
----After subsets= ['(((', '(()']
before subsets= ['(((', '(()']
----After subsets= ['((()', '(())']
before subsets= ['((()', '(())']
----After subsets= ['((()(', '((())', '(())(', '(()))']
before subsets= ['((()(', '((())', '(())(', '(()))']
----After subsets= ['((()((', '((()()', '((())(', '((()))', '(())((', '(())()', '(()))(', '(())))']
before subsets= ['((()((', '((()()', '((())(', '((()))', '(())((', '(())()', '(()))(', '(())))']
----After subsets= ['((()(()', '((()())', '((())()', '((())))', '(())(()', '(())())', '(()))()', '(()))))']
['((()(()','((()())','((())()','((())))','(())(()','(())())','(()))()','(()))))']

所有子序列获取并计算

写在前面，要一步一步来，先把基础打实了，再拓展和学习新的思路及方法！如果前面学习的还只是刚刚看懂，代码还是跟着打出来的，还不能自己顺畅的把代码打出来，就先不要着急去看AI推荐的其他算法，比如迭代，回溯等，这些事急不来，着急看新东西容易摔下去发现结果是啥也没搞明白。

牛客上的题，小红的子序列权值和_牛客题霸_牛客网
做了一下最多到5/32组用例通过，运行时间2001ms，内存占用4652KB，使用itertools+权值计算这种按部就班的方式，会超时，如果先把所有的子序列算出来，则会严重超内存

def generateweight(n):if n<=0 : return 0if n== 1: return 1ksum = 1;  k = int(n**0.5)+1for i in range(2, k):icnt = 0while n%i == 0:n //= iicnt += 1if icnt >0:ksum *=(icnt +1)if n > 1:ksum *= 2return ksumfrom itertools import combinations as comb ksum = 0
for i in range(1,len(arr)+1):comb1 = comb(arr,i)for x in comb1:mout = 1for y in x:mout *= ykk = generateweight(mout)ksum+=kkprint(ksum)

在如下的用例中就挂了，粗看一下，这里的n至少也超过25个了，所以回溯递归或二进制枚举肯定是不能用的。

查看了一下题解，代码如下，完全不是求出所有子序列然后调用函数求权值的思路，这里应该是数学上的计算方法，与我们讨论的内容无关。

from collections import Countern = int(input())
C = Counter(map(int, input().split()))
a, b, c = C[1], C[2], C[3]
mod = 1000000007
r = pow(2, n - 2, mod)
print((r * (b + 2) * (c + 2) - 1) % mod)

小结

这篇文章整理的内容较多，这段时间刷题和算法学习也算是拼了，只不过很明显的基础仍然不够牢，而且年纪大了，记忆力衰退的厉害，虽然已经循环复习但仍然很多写过的代码又忘记了，所以都需要总结下来，常常反复梳理。