当前位置：首页 > news >正文

微积分 | 外微分

news 2025/8/10 13:52:17

注：本文为 “微积分 | 外微分” 相关合辑。
图片清晰度受引文原图所限。
略作重排，未整理去重。
如有内容异常，请看原文。

如何通俗易懂地解释外微分？

Yuhang Liu

梯度这一概念对于许多人来说并不陌生，但梯度实际上是一个比外微分更“上层”的概念。这是因为外微分仅依赖于微分结构，而梯度的定义则需要度量结构，或者说是内积结构。如果仅考虑向量空间，那么在黎曼流形（若对黎曼流形不甚了解，可以将其视为一个内积空间，或者直接假设为 $Rn\mathbb{R}^n$ ）中，梯度 $∇f\nabla f$ 和全微分 $df\mathrm{d}f$ 互为对偶，即 $⟨∇f,X⟩=df(X)\langle \nabla f,X \rangle=\mathrm{d}f(X)$ 。从这个角度来看，可以将全微分 $df\mathrm{d}f$ 视为梯度的一种表现形式。

然而，这仅适用于函数的外微分。对于更高阶的微分形式的外微分，情况则有所不同。在 $R3\mathbb{R}^3$ 中，1 形式的外微分对应旋度，2 形式的外微分对应散度，而 3 形式的外微分恒为零，因为三维空间中不存在 4 形式。在这种框架下，可以发现 $R3\mathbb{R}^3$ 中的狭义斯托克斯公式和高斯散度定理实际上是广义斯托克斯定理的特例，即 $∫∂Dω=∫Ddω\int_{\partial D}\omega=\int_D\mathrm{d}\omega$ 。

尽管这种表述不够严格，但为了通俗易懂，不得不牺牲一定的严格性。严格定义外微分需要先定义微分形式，进而定义流形上的余切丛。此外，梯度和全微分在坐标分量上的简单对应关系仅适用于 $Rn\mathbb{R}^n$ 上的标准内积。若非标准内积，则需乘以系数矩阵。但对于希望获得通俗易懂解释的人来说，这些细节或许并不重要。许多人习惯将向量空间等同于 $Rn\mathbb{R}^n$ 并以点积作为内积，若向他们解释向量空间可以带有其他正定二次型作为内积，或者不带内积，他们可能会感到困惑。

当然，即使通俗易懂，理解外微分也需要一定的基础，即学过多元微积分。若未学过微积分或已遗忘，那么理解外微分将十分困难，毕竟理解任何知识都需要一定的门槛。

发布于 2017-12-16 23:39

若漂

要讨论外微分，必须明确两个概念：外微分形式（也称微分形式）和外微分算子 $d\mathrm{d}$ 。外微分算子可以视为一种运算符号。本文旨在阐述其起源与直观理解，以便读者在掌握数学语言后，能够顺利地将其严格表述出来。**学习数学需要两条腿走路：一方面要掌握数学语言，另一方面要理解其起源与直观含义，二者缺一不可且相互促进。**很多时候，直观理解能够帮助我们抓住问题的核心，而数学语言则如同翻译工具，能够将直观理解准确地表达出来。外微分的历史起源可以追溯到曲线积分与曲面积分，后来在现代微分几何中得到了进一步的发展与完善，这一过程在很大程度上得益于 E. Cartan 的杰出贡献。然而，若要从张量和张量积、外代数、切丛和余切丛等概念出发来定义微分流形上的微分形式和外微分算子，会使许多初学者望而却步，而且这些内容与外微分的核心思想并无直接关联。因此，本文主要从曲线积分与曲面积分的角度展开讨论，再结合对流形和纤维丛的理解，自然地过渡到微分流形的概念。

简化计算

本文中提到的曲线积分与曲面积分均为第二型积分，即带有方向的积分。具体而言，曲线积分可以理解为变力做功，而曲面积分则是流体流过给定曲面的流量。假设质点在力 $F⃗(x,y)=(P(x,y),Q(x,y))\vec{F}(x,y)=(P(x,y),Q(x,y))$ 的作用下在平面中运动，其轨迹为 $l$ ，则所做的功 $W$ 可表示为：

$W=∫lPdx+QdyW=\int_{l}P\mathrm{d}x+Q\mathrm{d}y$

若空间中流体的速度场为 $v⃗(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z))\vec{v}(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z))$ ，给定曲面 $Σ\Sigma$ ，则单位时间内的流量 $V$ 可表示为：

$V=∬ΣPdy∧dz+Qdz∧dx+Rdx∧dyV=\iint_{\Sigma}P\mathrm{d}y\wedge \mathrm{d}z+Q\mathrm{d}z\wedge \mathrm{d}x+R\mathrm{d}x\wedge \mathrm{d}y$

通过参数化表示，曲线积分和曲面积分可分别转化为定积分和二重积分（高维情况下对应为多重积分）。历史上引入外形式的一个重要原因是简化计算。例如，只需将 $dx=g′(t)dt\mathrm{d}x=g'(t)\mathrm{d}t$ 代入，即可得到定积分换元法公式（严格来说还需满足一些条件，此处暂不讨论，后续亦不再特别说明）：

$∫abf(x)dx=∫t1t2f(g(t))∣g′(t)∣dt\int_{a}^{b}f(x)\mathrm{d}x=\int_{t_{1}}^{t_{2}}f(g(t))|g'(t)|\mathrm{d}t$

然而，当涉及到二重积分时，情况会变得复杂。假设 $x = x (u, v)$ ， $y = y (u, v)$ ，则变量代换公式为：

$∬Df(x,y)dxdy=∬D′f(x(u,v),y(u,v))∣∂(x,y)∂(u,v)∣dudv\iint_{D}f(x,y)\mathrm{d}x\mathrm{d}y=\iint_{D'}f(x(u,v),y(u,v))\Bigg|\frac{\partial(x,y)}{\partial(u,v)}\Bigg|\mathrm{d}u\mathrm{d}v$

此时， $dx=∂x∂udu+∂x∂vdv\mathrm{d}x=\frac{\partial x}{\partial u}\mathrm{d}u+\frac{\partial x}{\partial v}\mathrm{d}v$ ， $dy=∂y∂udu+∂y∂vdv\mathrm{d}y=\frac{\partial y}{\partial u}\mathrm{d}u+\frac{\partial y}{\partial v}\mathrm{d}v$ 。直接代入无法得到变量代换公式。但如果引入运算关系 $du∧du=0=dv∧dv\mathrm{d}u\wedge \mathrm{d}u=0=\mathrm{d}v\wedge \mathrm{d}v$ ， $du∧dv=−dv∧du\mathrm{d}u\wedge \mathrm{d}v=-\mathrm{d}v\wedge \mathrm{d}u$ ，则可得到：

$dx∧dy=(∂x∂u∂y∂v−∂x∂v∂y∂u)du∧dv\mathrm{d}x\wedge \mathrm{d}y=\left(\frac{\partial x}{\partial u}\frac{\partial y}{\partial v}-\frac{\partial x}{\partial v}\frac{\partial y}{\partial u}\right)\mathrm{d}u\wedge \mathrm{d}v$

这样直接代入就不存在问题了。我们将 $du,dv\mathrm{d}u,\mathrm{d}v$ 之间满足上述运算性质的乘法称为外积，用符号 $∧\wedge$ 表示。类似地，推广到高维也是可行的。

有向被积单元

上文从简化运算的角度探讨了外形式的起源，那么为何要如此定义微分之间的运算？为何将这种运算称为外积？它与之前学过的向量外积有何关联？接下来，我们将结合几何与物理含义进行说明。 $dxdy\mathrm{d}x\mathrm{d}y$ 是面积元，而微分形式旨在将面积元的符号（正负）也纳入考虑范围，简而言之， $dx∧dy\mathrm{d}x\wedge \mathrm{d}y$ 是有向面积元。以下通过曲面积分的例子进行具体说明。

假设空间中流体的速度场为 $v⃗(x,y,z)=(P(x,y,z),0,0)\vec{v}(x,y,z)=(P(x,y,z),0,0)$ ，即流体仅沿 $x$ 轴方向流动， $P > 0$ 表示沿 $x$ 轴正向流动，反之则沿负向流动，而沿 $y, z$ 轴的速度分量均为零。给定 $y O z$ 平面内的区域 $Σ\Sigma$ ，则单位时间内的流量 $V$ 可表示为：

$V=∬ΣPdy∧dzV=\iint_{\Sigma}P\mathrm{d}y\wedge \mathrm{d}z$

需要注意的是，此处的 $Σ\Sigma$ 是带有方向的，我们规定沿 $x$ 轴正向穿过它为正。积分 $∬ΣPdy∧dz\iint_{\Sigma}P\mathrm{d}y\wedge \mathrm{d}z$ 如何理解呢？如果速度与空间位置无关，那么单位时间内的流量就是速度与区域面积的乘积。当速度与空间位置有关时，可将区域分割成无数个无穷小的矩形，每个矩形的长为 $dy\mathrm{d}y$ 、宽为 $dz\mathrm{d}z$ （相应地，面积为 $dydz\mathrm{d}y\mathrm{d}z$ ），在无穷小的尺度下，速度不再变化，因此，每个小矩形提供的流量就是 $PdydzP\mathrm{d}y\mathrm{d}z$ ，将其称为被积单元，总流量就是将所有被积单元相加，即积分 $∬ΣPdy∧dz\iint_{\Sigma}P\mathrm{d}y\wedge \mathrm{d}z$ 。

然而，这种方法存在一个缺点，即方向并未蕴含在被积单元中，需要人为判断，当区域不包含在某一平面内时，不同部分积分的正负号也可能不同。而将方向蕴含其中，就得到了外微分形式，其实质是有向被积单元。将 $dy\mathrm{d}y$ 视为沿 $y$ 轴方向的正无穷小量 $(dy,0)(\mathrm{d}y,0)$ ， $dz\mathrm{d}z$ 视为沿 $z$ 轴正向的无穷小向量 $(0,dz)(0,\mathrm{d}z)$ ，那么 $dy×dz\mathrm{d}y\times \mathrm{d}z$ 也是一个向量，其模长是 $dy,dz\mathrm{d}y,\mathrm{d}z$ 张成的矩形（一般情况下为平行四边形）的面积，用坐标表示向量时是一行列式的绝对值，方向可以通过右手定则判定，沿 $x$ 轴正向。流速本身也是一个向量，与 $dy×dz\mathrm{d}y\times \mathrm{d}z$ 做内积即可得到有向被积单元。不过，这需要将 $P$ 和 $dy×dz\mathrm{d}y\times \mathrm{d}z$ 都视为向量， $P$ 实际上是 $Pi⃗P\vec{i}$ ，其中 $i⃗\vec{i}$ 是沿 $x$ 轴正向的单位向量，有向被积单元为 $Pi⃗⋅(dx×dy)P\vec{i}\cdot (\mathrm{d}x\times \mathrm{d}y)$ ，这还不够方便。干脆将 $i⃗⋅(dx×dy)\vec{i}\cdot (\mathrm{d}x\times \mathrm{d}y)$ 视为一个整体，用坐标表示向量时是一行列式的值，这就是如今的外微分形式，它带有方向，但并非向量，方向表现为正号或负号。这是二维情形，如果是三维，将 $dx\mathrm{d}x$ 视为 $(0,0,dx)(0,0,\mathrm{d}x)$ ， $dy\mathrm{d}y$ 视为 $(0,dy,0)(0,\mathrm{d}y,0)$ ， $dz\mathrm{d}z$ 视为 $(0,0,dz)(0,0,\mathrm{d}z)$ ，这三个向量形成一个平行六面体（在两两正交的情况下是长方体），其有向体积可以用向量的混合积表示： $dx⋅(dx×dy)\mathrm{d}x\cdot (\mathrm{d}x\times \mathrm{d}y)$ 。如果将向量用坐标表示，那么有向积分的代数表示就是这些坐标形成的行列式的值（这是行列式的几何含义），这种代数表述便于向高维推广。

定义成反对称双线性函数

然而，现代数学无法直接处理无穷小量，因此需要将无穷小量在线性关系下进行宏观化处理，利用线性空间刻画出相应的性质，并在求积分时借助极限进行表述。具体来说， $dy∧dz\mathrm{d}y\wedge \mathrm{d}z$ 是无穷小有向面积，难以直接说明，于是将 $dy∧dz\mathrm{d}y\wedge \mathrm{d}z$ 定义为求有向面积的运算。在 $y O z$ 平面中，对于任意两个向量 $ξ1⃗,ξ2⃗\vec{\xi_{1}},\vec{\xi_{2}}$ ，均有：

$dy∧dz(ξ1⃗,ξ2⃗)=i⃗⋅(ξ1⃗×ξ2⃗)\mathrm{d}y\wedge \mathrm{d}z(\vec{\xi_{1}},\vec{\xi_{2}})=\vec{i}\cdot(\vec{\xi_{1}}\times\vec{\xi_{2}})$

这样， $dy∧dz\mathrm{d}y\wedge \mathrm{d}z$ 就成为 $y O z$ 平面的反对称双线性函数，这正是我们如今所见的定义。

微分形式的介绍暂且到此为止，后续有机会再详细阐述外微分算子。

发布于 2020-12-27 16:25

菜场学院菜老师

外微分和同调是两条同步发展的脉络：

外微分：线性对偶空间、(任意可微函数的)局部(函数芽)线性化、线性函数的等价类(商掉常数的差异——类比不定积分的任意常数)、微分形式、楔积构造分次代数、外代数、张量；
同调：单纯形、自由生成群、正合序列、同调群；

这两条脉络分别依靠外微分算子 $d\mathrm{d}$ 和边界算子 $∂\partial$ 构成了不同的同态序列：

$d:Ωk−1(M)⟶dk−1Ωk(M)⟶dkΩk+1(M)∂:Ck⟶∂kCk−1⟶∂k−1Ck−2(1)\begin{align} \mathrm{d}: &\Omega^{k-1}(M) \stackrel{\mathrm{d}^{k-1}}{\longrightarrow} \Omega^k(M) \stackrel{\mathrm{d}^k}{\longrightarrow} \Omega^{k+1}(M) \\ \partial: &C_k \stackrel{\partial_k}{\longrightarrow} C_{k-1} \stackrel{\partial_{k-1}}{\longrightarrow} C_{k-2} \end{align} \tag{1}$

这两个算子在同态方向上的对偶性是同调群和 de Rham 上同调的基础。简单地说，外微分和同调在发展过程中相互交汇，构成了斯托克斯定理：

$∫Ddω=∫∂Dω\int_D \mathrm{d}\omega = \int_{\partial D} \omega$

或者更紧凑地写成对偶的双线性映射 $⟨D,dω⟩=⟨∂D,ω⟩\langle D, \mathrm{d}\omega \rangle = \langle \partial D, \omega \rangle$ ，暗示了整体算子 $∂\partial$ 和局部算子 $d\mathrm{d}$ 之间的对偶关系。

斯托克斯定理联系了两者，但这并不意味着可以通过斯托克斯定理从同调自动得到外微分！

问题下有好几个高赞回答存在一种倾向，即不必从根本上理解外微分，而是通过斯托克斯定理来得到外微分，这是错误的：

斯托克斯定理无法保证外微分的存在性和唯一性，因此无法借助斯托克斯定理从同调或流形的边界性质定义出外微分；
外微分本身是一个代数概念，并不需要斯托克斯定理中出现的积分来诱导。从逻辑上看，应该是先有了外微分的概念，然后再定义微分形式的积分——这种定义可以直接借鉴重积分，然后才能讨论三角剖分上对微分形式的积分，最后过渡到斯托克斯定理上的奇异复形上对微分形式的积分。

对外微分的理解

从根本上理解外微分，建议从张量入手。张量是一个复杂但重要的概念，以下是几点关键的理解方向：

先理解代数上的对偶空间，即明确行向量和列向量的区别与联系；
若在微分流形上难以理解某些概念，可以先在线性空间上理解，虽然这样会显得较为平凡，但有助于快速建立直观理解；
许多自称为对读者友好的微分几何教科书，往往是先引入切空间，再用对偶空间定义余切空间。然而，这种理解方式下的余切空间和微分形式缺乏直观性。建议参考陈省身的微分几何讲义，从函数的局部线性化入手，用商空间的方式定义余切空间。虽然这种方法较为抽象，但能够真正帮助读者深入理解；
外微分与外代数（Grassmann 代数）密切相关。外代数是一种分次代数，每个阶都构成封闭的子空间，这种结构通过楔积 $∧\wedge$ 构造。实际上，分次代数的本质并非楔积，而是张量代数本身具有的——张量代数是依靠张量积 $⊗\otimes$ 构造的分次代数。因此，要先理解如何通过张量积将不同阶的张量空间搭建出张量代数，再理解作为张量代数中子代数的外代数。这样，在讨论反对称的协变张量这一概念时，才不至于感到困惑。

发布于 2018-11-29 11:28

not 狐

外微分形式最简单的理解就是有向线元/面元。学过斯托克斯公式和高斯公式的人应该对此并不陌生。

那么，为何要定义外微分呢？这需要先了解我们为何需要 Grassmann 代数。

主要原因在于传统的内积/叉积定义存在诸多问题：传统内积的定义满足交换律，这导致我们无法区分方向，即无法明确是“你乘我”还是“我乘你”；并且在定义叉积时，为了方便记忆，直接硬性规定两个向量的叉积结果是垂直于这两个向量的另一向量。这两点结合，导致我们在进行计算时，无法机械化、自动化地区分极矢量和轴矢量（或说矢量和赝矢量）。因此，在计算过程中，我们竟然会误以为面元的法矢量和线元矢量是同一回事。

这就直接导致了，明明在拓扑上斯托克斯公式和高斯公式讲的是同一个问题，但呈现出的公式却大相径庭，非常丑陋。

那该如何解决呢？

很简单，把丑陋的叉积和内积全部换成一个“楔积”即可，从而我们便得到了 Grassmann 代数。

外微分，就是研究 Grassmann 代数中的微分性质。

外微分形式，就是外微分中的微元，与传统多元微积分中的微元不同，它天生带有方向。

引入外微分后，有以下几点显著优势：

原本分散的梯度、散度、旋度三大运算，居然统一成了一种微分运算！
原本形式各异的斯托克斯公式、高斯公式（以及附赠的格林公式），居然统一成了一种形式！

从而，我们终于可以向高维拓展，获得更广义的理论了，再也不用担心高维微积分了。

编辑于 2022-03-20 18:37

qfzklm

外微分本质上是一个区域和其边界之间的对应关系。

我们熟知的微积分基本定理（牛顿 - 莱布尼茨公式）就是将一段直线区域上的积分对应到这段直线的端点上。同样地，格林公式将一个二维平面区域上的积分对应到该区域的边界上，高斯公式将一个三维体积区域的积分对应到该区域的表面上。总之，在外微分出现之前，我们已经熟悉了这种“区域和其边界的对应”。

剩下的问题是如何恰当地描述这种对应关系，以及如何将这种对应关系推广到任意维度的空间和不同的坐标系统（即流形）上。于是，我们找到了多重线性反对称的外微分。

发布于 2017-12-07 19:56

外微分究竟为什么是可行的？

关于外微分形式的疑问

外代数的构建过程

对偶空间：先定义对偶空间及其线性函数
张量积：定义对偶空间线性函数的张量积（作为多重线性函数的特例）
外积构造：
- 通过张量积+反对称化定义 $r$ 重线性函数的外积
- 满足分配律、结合律和反交换律
空间结构：
- 对偶空间的 $r$ 重反对称张量空间基： $n$ 取 $r$ 的外积基（共 $C_n^r$ 个）
- 由此抽象出外代数、外多项式、外微分形式

现有理解

$dx∧dy\mathrm{d}x \wedge \mathrm{d}y$ 中的微分实为切空间坐标函数（线性函数）
通过雅可比行列式验证外积合理性（与可定向体积微元关联）
行列式作为多重反对称函数的特例

未解疑问

1. 外积与经典微分算子

为何 $dxdydz\mathrm{d}x\mathrm{d}y\mathrm{d}z$ 作为反对称线性函数能导出：
- 雅可比行列式（已理解）
- 旋度和散度（未理解）
外微分形式的定义如何自然对应到这些物理量？

2. 外积积分的本质

$dx∧dy\mathrm{d}x \wedge \mathrm{d}y$ 本质是反对称线性函数：
- 外积运算：生成新的反对称函数
- 实际积分时：为何退化成经典"微元"概念？
函数→量的"退化"如何严格理解？

3. 坐标函数的关键性

为何大多教材不强调 $dx\mathrm{d}x$ , $dy\mathrm{d}y$ 的线性函数本质？
外积的合法性是否依赖于：
- 微分作为线性函数的性质？
- 对偶空间的结构特性？

我心永恒

75 人赞同了该回答

整个逻辑链是：

旋度和散度的推导
多重线性函数
多重反对称线性函数（外积与行列式）
外微分形式的外微分的几何意义

总结

外微分形式中的外积，不是某个微元向量的坐标量 $dx,dy\mathrm{d}x,\mathrm{d}y$ ，以及 $dP,dQ\mathrm{d}P,\mathrm{d}Q$ 等等，而是几个微元向量的一些微元量，构成的行列式函数：

$(f1∧f2∧⋯∧fr)(v⃗1,…,v⃗r)=f1(v⃗1)∧f2(v⃗2)∧⋯∧fr(v⃗r)=∣f1(v⃗1)…f1(v⃗r)⋮⋮⋮fr(v⃗1)…fr(v⃗r)∣\begin{align*} (f_1 \wedge f_2 \wedge \dots \wedge f_r)(\vec{v}_1, \dots, \vec{v}_r) &= f_1(\vec{v}_1) \wedge f_2(\vec{v}_2) \wedge \dots \wedge f_r(\vec{v}_r) \\ &= \begin{vmatrix} f_1(\vec{v}_1) & \dots & f_1(\vec{v}_r) \\ \vdots & \vdots & \vdots \\ f_r(\vec{v}_1) & \dots & f_r(\vec{v}_r) \end{vmatrix} \end{align*}$

$r$ 个线性函数 $f1,f2,…,frf_1, f_2, \dots, f_r$ 对 $r$ 个向量 $v⃗1,v⃗2,…,v⃗r\vec{v}_1, \vec{v}_2, \dots, \vec{v}_r$ 的外积运算。其结果是一个行列式，这个行列式表示的是这些向量在这些线性函数下的某种“体积”或“定向面积”。

由于自变量向量任意，所以被省略了。这个省略恰恰隐藏了几何意义，而让人感觉外微分是凑巧满足了分配律和反交换律的外代数，从而去机械和抽象地理解它，这肯定是不对的。它的运算律：分配律和反交换律都是行列式的性质，完全就是行列式，并不比行列式更深奥。而行列式的几何意义就非常明显。比如 $dx∧dy\mathrm{d}x\wedge\mathrm{d}y$ ，你可以把 $dx\mathrm{d}x$ 等等看做这个二阶行列式的一个列向量（或者行向量）。此时 $dx\mathrm{d}x$ 就是向量，只不过包含了两个向量的 $dx\mathrm{d}x$ 坐标。当然要说几何意义，要把它转置过来，形成

$det⁡(向量1,向量2)=det⁡(dx1dy1dx2dy2)\det(\text{向量}1, \text{向量}2) = \det\begin{pmatrix} \mathrm{d}x_1 & \mathrm{d}y_1 \\ \mathrm{d}x_2 & \mathrm{d}y_2 \end{pmatrix}$

这就是两个向量形成的微元平行四边形的面积。只不过恰好转置和不转置相等罢了。所以 $dx\mathrm{d}x$ 可以看做向量。外积运算就相当于这些向量构成行列式的顺序。当然这只是外积的特殊情况，外积不必限于此，只不过行列式是外积运算的结果。

外微分形式的外微分 $d(pdx+…)\mathrm{d}(p\mathrm{d}x+\ldots)$ 的几何意义： $dP∧dx\mathrm{d}P\wedge\mathrm{d}x$ 是二阶行列式，其实就是在某点附近，任意两个自变量向量的微小平行四边形的 $P$ 分量的环量，剩下分量同理，再叠加，就是总环量； $dP∧dy∧dz\mathrm{d}P\wedge\mathrm{d}y\wedge\mathrm{d}z$ 是三阶行列式，其实就是在某点附近，任意三个自变量向量构成的微小平行六面体向外表面 $P$ 分量的通量，再叠加 $Q$ 、 $R$ 分量的通量，得到总通量。加起来是因为向量的环量通量是对向量叠加的。

外微分形式的外微分就非常自然了，首先比如线积分，可以分开看 $PQR$ 的线积分。线积分环绕一个微小平行四边形计算出来就是变成了 $dp∧dx\mathrm{d}p\wedge\mathrm{d}x$ ，等等（详细见以下），所以定义是合理的。然后将 $dp\mathrm{d}p$ ， $dq\mathrm{d}q$ ， $dr\mathrm{d}r$ 带入就得出旋度，分配和反交换的运算就是行列式的列的性质的运算。散度同理。

完整版

向量场 $v⃗=f(r⃗)\vec{v} = f(\vec{r})$ ，对于某一个点 $r⃗0\vec{r}_0$ ，线性化之后是

$dv⃗=(∂P∂x∂P∂y∂P∂z∂Q∂x∂Q∂y∂Q∂z∂R∂x∂R∂y∂R∂z)dr⃗=Jdr⃗\mathrm{d} \vec{v} = \begin{pmatrix} \frac{\partial P}{\partial x} & \frac{\partial P}{\partial y} & \frac{\partial P}{\partial z} \\ \frac{\partial Q}{\partial x} & \frac{\partial Q}{\partial y} & \frac{\partial Q}{\partial z} \\ \frac{\partial R}{\partial x} & \frac{\partial R}{\partial y} & \frac{\partial R}{\partial z} \end{pmatrix} \mathrm{d} \vec{r} = J \mathrm{d} \vec{r}$

1. 旋度的推导

一个准备工作：一个常向量叉积任意向量其实是线性变换，它的矩阵表示是反对称矩阵，反对称矩阵的对角线元素为零，非对角线元素相反。

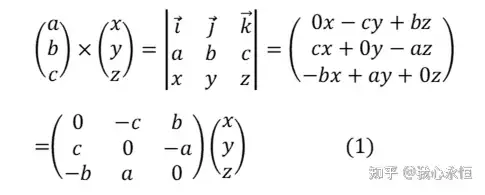
在这里插入图片描述

反过来每一个反对称矩阵也给出了一个叉乘向量，看一下雅克比矩阵：

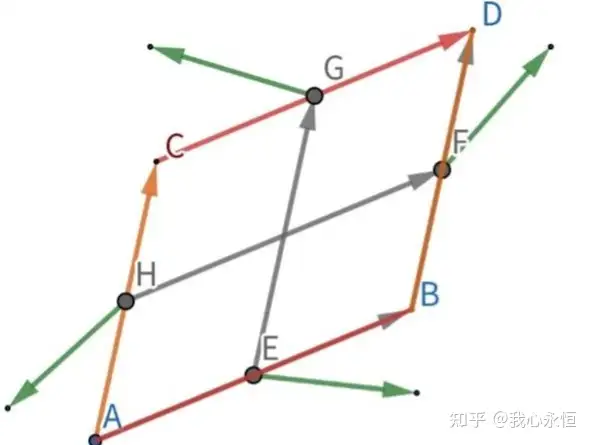
在这里插入图片描述

旋度似乎就出来了。接下来仔细推导。

既然已经考虑了无穷小，在三维空间中计算曲面上某小区域的环量实际上可以在这点的切面上进行，而且只用计算切面上的小平行四边形的环量了，而不用考虑任意曲线的环量。即局部线性化和以直代曲。

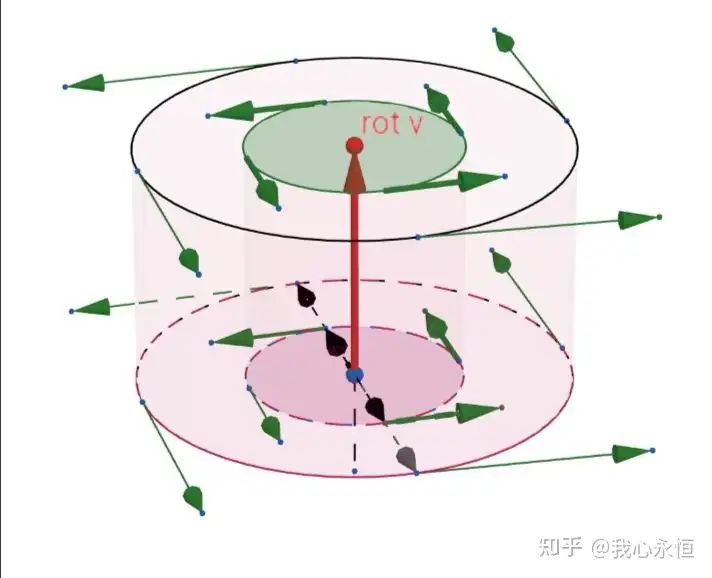
在这里插入图片描述

实际上对于闭合曲线的向量场的环量，常向量是不重要的，因为它的环量一定是零。所以旋散度只取决于微分变化量。如果 $v$ 是速度场，对于旋度，其实就是 2 倍角速度，这也是旋的意思，为什么有个 2 呢？因为任何一个方阵都可以唯一分解为一个反对称矩阵和对称矩阵的和。

所以 $12\frac{1}{2}$ 就出现了。因为根据式（1），旋度和 2A 对应，即： $vJ-J^T \leftrightarrow \text{rot } v$

由于环量对向量场的叠加性，所以加法分解是合适的。而且也可以通过上面的推导看出 $d v 2$ 的旋度为零。

根据 A 场变化量的公式 $\text{rot } v \times dr$ ，分解出的 $d v 1$ 场变化量就像一个物体匀速转动的速度场。根据 A 场变化量的公式，旋度大小其实就是二倍角速度，方向就是一个物体旋转轴的方向。

在这里插入图片描述

某点附近，旋度是 2 倍角速度。而向量场对这点的第一部分变化量相当于物体绕旋度匀速转动的速度场。

在这里插入图片描述

2. 散度的推导

接下来就看这个对称矩阵 $B$ 。对称矩阵也有非常好的性质，它有三个相互正交的单位特征向量。

在这里插入图片描述

先算 $B$ 部分的散度：

在这里插入图片描述

推出来的散度实际就是矩阵 $B$ 或 $J$ 的迹，也就是对角线元素之和。接下来推导 $A$ 的散度：

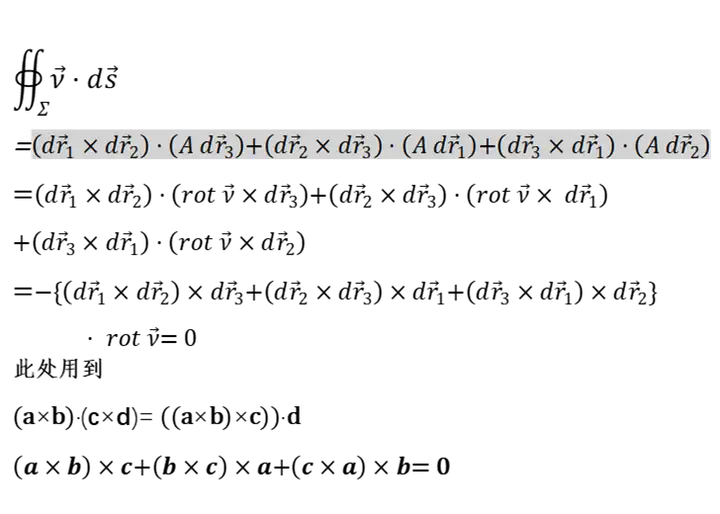
在这里插入图片描述

后面将这个推导稍微改变一下就能得出外微分。

所以整体上， $J$ 的旋度就是 $A$ 的旋度， $J$ 的散度就是 $B$ 的散度。所以这个矩阵分解是完全把散度旋度分开了。 $A$ 是有旋无散场， $B$ 是有散无旋场。由此，微分公式可以变为

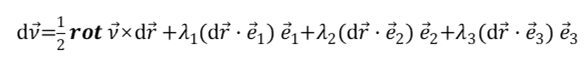
在这里插入图片描述

$dv⃗=A+B\mathrm{d} \vec{v} = A + B$

对于整个场，也可以分解为一个有旋无散场和有散无旋场，这被称为赫姆霍兹分解定理。

3. 多重线性函数

上面的一些推导对于理解外积是重要的。要理解外积运算 $∧\wedge$ ，先从多重线性函数来理解。

例如，三重线性函数

$f(v⃗1,v⃗2,v⃗3)=rf(\vec{v}_1, \vec{v}_2, \vec{v}_3) = r$

其中 $r$ 是实数。多重的意思就是有多个自变量，只不过这里自变量是向量。而多元函数每一个自变量都是实数，所有实数其实可以合并为一个向量，而这里是多个向量。而且对每一个变量都是线性的，和线性函数的性质类似。

几个单重线性函数的乘积也构成了一个多重线性函数，反过来不一定对。

这个乘积其实是张量积，和通常函数的乘积不一样的地方是两个函数自变量是独立的，它满足结合律和分配律，不满足交换律。比较一下

在这里插入图片描述

对偶空间：

对偶空间就是线性空间 $V$ 上的（单重）线性函数的集合。它是线性映射的特殊情况，其实就是在 $V$ 的某组基下的 1 行 $n$ 列矩阵。线性函数也可以有加和数乘运算，这两个运算也是封闭的。所以对偶空间是线性空间，维数和 $V$ 一样。选定 $V$ 上的一组基之后就是规定对偶基，也就是 $V$ 上任意向量在这组基下的 $n$ 个坐标分量函数，每一个函数只取一个坐标。线性函数和内积相似。 $dx∧dy\mathrm{d}x\wedge\mathrm{d}y$ 中的 $dx\mathrm{d}x$ ， $dy\mathrm{d}y$ 就是自变量为 $dr\mathrm{d}r$ 的坐标分量函数。 $dP,dQ,dR\mathrm{d}P,\mathrm{d}Q,\mathrm{d}R$ 也是单重线性函数，因为它们是 $dxdydz\mathrm{d}x\mathrm{d}y\mathrm{d}z$ 的线性组合。

在这里插入图片描述

重要的是要明白外微分形式中的微分其实是函数，而不一定是通常的一个坐标轴自变量 $x yz$ 的微分。在外微分的运算中并没有标出自变量，这才有点混淆，看不清它到底运算的是什么。加上自变量之后，我们就知道了外微分运算的意义。

4. 多重反对称线性函数

多重线性函数，加上一个反对称，即任意交换两个向量函数变号，就是多重反对称线性函数。

行列式就是这样的，行列式代表体积，每一列都是线性的，交换两行（列）反号。

外微分形式中的外积，准确表达式应该是一个行列式函数：

在这里插入图片描述

$dx1∧dx2∧⋯∧dxr=det⁡(dx1(v⃗1)dx1(v⃗2)⋯dx1(v⃗r)dx2(v⃗1)dx2(v⃗2)⋯dx2(v⃗r)⋮⋮⋱⋮dxr(v⃗1)dxr(v⃗2)⋯dxr(v⃗r))\mathrm{d}x^1 \wedge \mathrm{d}x^2 \wedge \cdots \wedge \mathrm{d}x^r = \det\begin{pmatrix} \mathrm{d}x^1(\vec{v}_1) & \mathrm{d}x^1(\vec{v}_2) & \cdots & \mathrm{d}x^1(\vec{v}_r) \\ \mathrm{d}x^2(\vec{v}_1) & \mathrm{d}x^2(\vec{v}_2) & \cdots & \mathrm{d}x^2(\vec{v}_r) \\ \vdots & \vdots & \ddots & \vdots \\ \mathrm{d}x^r(\vec{v}_1) & \mathrm{d}x^r(\vec{v}_2) & \cdots & \mathrm{d}x^r(\vec{v}_r) \end{pmatrix}$

其实就是多个线性函数的张量积的 $r!$ 个的和。这样我们就能理解外积的反交换律，因为行列式交换两行变号。分配律，因为行列式对每一行的线性。所以对它的外积运算才有点像向量。当然还有个结合律，不过这里看不出来，因为式（7）不是一个定义式而是一个推导式。 $∧\wedge$ 是一个二元运算符，作用对象是一个 $r$ 重线性函数和一个 $s$ 重线性函数，得出两者的（张量）积，也就是一个 $r + s$ 重线性函数，再反对称得到结果。所以外积包含两个运算，先张量积再反对称化。反对称化其实就是重排函数的自变量的顺序，根据排列奇偶性来决定正负，来求和，就像上面的行列式一样。严格定义和推导见附录。用式（7）去理解外微分就够了，其实它作为外积的定义也未为不可。

5. 外微分的几何意义

外微分中的外积运算和旋度、散度，以及外微分形式的外微分如 $d(Pdx+Qdy+Rdz)=dP∧dx+dQ∧dy+dR∧dz\mathrm{d}(P\mathrm{d}x+Q\mathrm{d}y+R\mathrm{d}z)=\mathrm{d}P\wedge\mathrm{d}x+\mathrm{d}Q\wedge\mathrm{d}y+\mathrm{d}R\wedge\mathrm{d}z$ ，为什么那么定义，那么凑巧与旋度有关，它得出的是什么？

先看看多重积分的面积体积元素

在这里插入图片描述

这样我们理解了它为什么得出雅可比行列式，雅可比行列式就是面积之比。 $dx∧dy\mathrm{d}x\wedge\mathrm{d}y$ 其实就是 $uv$ 坐标系中两个向量变换之后张成的四边形的面积。 $du∧dv\mathrm{d}u\wedge\mathrm{d}v$ 就是这两个原始向量的面积。当 $dl1\mathrm{d}l_1$ 平行与 $u$ 轴， $dl2\mathrm{d}l_2$ 平行于 $v$ 轴就得到函数的退化为两个普通微分乘积 $dudv\mathrm{d}u\mathrm{d}v$ ，也就是多重积分中的面积体积微元。但此时 $dx∧dy\mathrm{d}x\wedge\mathrm{d}y$ 不是这样一个长方形，而是 $dudv\mathrm{d}u\mathrm{d}v$ 长方形变换后的，通常是平行四边形。

将旋度散度的推导稍微变形一下就能得出斯托克斯公式（Stokes 公式）：

在这里插入图片描述

如此就能彻底理解外微分定义为什么可以得出旋度散度。 $dP∧dx\mathrm{d}P\wedge\mathrm{d}x$ 是二重反对称线性函数，其实就是在某点附近，任意两个自变量向量的微小平行四边形的 $P$ 分量的环量，剩下分量同理，再叠加，就是总环量； $dP∧dy∧dz\mathrm{d}P\wedge\mathrm{d}y\wedge\mathrm{d}z$ 是三重反对称线性函数，其实就是在某点附近，任意三个自变量向量构成的微小平行六面体向外表面 $P$ 分量的通量，再叠加 $Q$ $R$ 分量的通量，得到总通量。加起来是因为向量的环量通量是对向量叠加的。

试一下一个高斯公式的变体：

在这里插入图片描述

附录

（陈维桓《微分几何初步》）

在这里插入图片描述

编辑于 2022-06-05 20:07

外微分：简化多变量微积分中的公式、简化热统中公式、简化非阿贝尔规范场的表述

魏贤昊

2022 年 5 月 12 日

1 外微分

陈省身十分深刻指出，多变量微积分与单变量微积分的根本差别是前者有外微分形式，而不巧的是外微分这一概念被剔除出了多变量微积分教材。但是数学发展常常是更高级更简单的概念出现在更低级更复杂的概念之后。外微分作为一个高级概念，它用一个公式统一了 Stokes、Green、Gauss、Newton-Leibniz 公式，且用一个公式统一了热统中一系列繁杂的公式。Hilbert 说外微分形式是 “更有力的工具和更简单的方法”，因此值得在本篇文章中提出来引起大家的重视，并期望之后能回归到微积分教材中去。

外微分概念起源于积分中的定向。从 A 到 B 的线积分，和从 B 到 A 的线积分中间差了符号，有

$∫abf(x)dx=−∫baf(x)dx.\int_{a}^{b} f (x) \, dx = -\int_{b}^{a} f (x) \, dx.$

而关于曲面如何定向的问题，我们这样来看。对于一个被定向了的曲面 D，有

$∬Df(x,y)dxdy=∬D′f(x(u,v),y(u,v))∂(x,y)∂(u,v)dudv.\iint_{D} f (x,y) \, dx \, dy = \iint_{D'} f (x (u,v), y (u,v)) \frac {\partial (x,y)}{\partial (u,v)} \, du \, dv.$

我们通过此完成了对二维曲面的定向，满足上述两条规则的微分乘积叫微分的外积，记作 $dx \wedge dy$ ，引入外积运算

$dx∧dx=0,dy∧dy=0,dz∧dz=0,dx∧dy=−dy∧dx,dy∧dz=−dz∧dy,dz∧dx=−dx∧dz,(dx∧dy)∧dz=dx∧(dy∧dz).\begin {aligned} dx \wedge dx &= 0, \\ dy \wedge dy &= 0, \\ dz \wedge dz &= 0, \\ dx \wedge dy &= -dy \wedge dx, \\ dy \wedge dz &= -dz \wedge dy, \\ dz \wedge dx &= -dx \wedge dz, \\ (dx \wedge dy) \wedge dz &= dx \wedge (dy \wedge dz). \end {aligned}$

Poincare 引理：若 $ω\omega$ 为一外微分形式，其微分形式的系数具有二阶连续偏导数，则 $(d\omega) = 0$ ，即边界没有边界。

Poincare 逆定理：若 $ω\omega$ 是一个 p 次外微分形式，且 $dω=0d\omega = 0$ ，则存在一个 p-1 次外微分形式 $α\alpha$ ，使得 $ω=dα\omega = d\alpha$ 。

同时我们定义一个外微分运算，定义式一为

$\frac {\partial f}{\partial x} dx + \frac {\partial f}{\partial y} dy + \frac {\partial f}{\partial z} dz.$

同时我们定义的这个外微分运算定义式二为

外微分作用下积分运算满足

$∫∂Σω=∫Σdω.\int_{\partial \Sigma} \omega = \int_{\Sigma} d\omega.$

由此我们可以得到斯托克斯公式

$dω=(∂P∂xdx+∂P∂ydy+∂P∂zdz)∧dx+(∂Q∂xdx+∂Q∂ydy+∂Q∂zdz)∧dy+(∂R∂xdx+∂R∂ydy+∂R∂zdz)∧dz,dω=(∂R∂y−∂Q∂z)dy∧dz+(∂P∂z−∂R∂x)dz∧dx+(∂Q∂x−∂P∂y)dx∧dy,∫∂Σω=∫Σdω.\begin {aligned} d\omega &= \left ( \frac {\partial P}{\partial x} dx + \frac {\partial P}{\partial y} dy + \frac {\partial P}{\partial z} dz \right) \wedge dx + \left ( \frac {\partial Q}{\partial x} dx + \frac {\partial Q}{\partial y} dy + \frac {\partial Q}{\partial z} dz \right) \wedge dy + \left ( \frac {\partial R}{\partial x} dx + \frac {\partial R}{\partial y} dy + \frac {\partial R}{\partial z} dz \right) \wedge dz, \\ d\omega &= \left ( \frac {\partial R}{\partial y} - \frac {\partial Q}{\partial z} \right) dy \wedge dz + \left ( \frac {\partial P}{\partial z} - \frac {\partial R}{\partial x} \right) dz \wedge dx + \left ( \frac {\partial Q}{\partial x} - \frac {\partial P}{\partial y} \right) dx \wedge dy, \\ \int_{\partial \Sigma} \omega &= \int_{\Sigma} d\omega. \end {aligned}$

由此我们可以得到高斯公式

$ω=Pdy∧dz+Qdz∧dx+Rdx∧dy,dω=dP∧dy∧dz+dQ∧dz∧dx+dR∧dy,dω=(∂P∂x+∂Q∂y+∂R∂z)dx∧dy∧dz,∫∂Σω=∫Σdω.\begin {aligned} dx \wedge dy \wedge dx &= (-dy \wedge dx) \wedge dx = -dy \wedge (dx \wedge dx) = 0, \\ \text {when } \omega &= P dy \wedge dz + Q dz \wedge dx + R dx \wedge dy, \\ d\omega &= dP \wedge dy \wedge dz + dQ \wedge dz \wedge dx + dR \wedge dy, \\ d\omega &= \left ( \frac {\partial P}{\partial x} + \frac {\partial Q}{\partial y} + \frac {\partial R}{\partial z} \right) dx \wedge dy \wedge dz, \\ \int_{\partial \Sigma} \omega &= \int_{\Sigma} d\omega. \end {aligned}$

以上两个公式对应外微分的 2-form 和 3-form。外微分的 1-form、2-form、3-form 一般使用范围如下

$1-form(Ω1(M)):ω=∑ifidxi,2-form(Ω2(M)):ω=∑ijfijdxi∧dxj,3-form(Ω3(M)):ω=∑ijkfijkdxi∧dxj∧dxk.\begin {aligned} 1\text {-form} (\Omega^{1}(M)) & : \omega = \sum_{i} f_{i} dx^{i}, \\ 2\text {-form} (\Omega^{2}(M)) & : \omega = \sum_{i j} f_{i j} dx^{i} \wedge dx^{j}, \\ 3\text {-form} (\Omega^{3}(M)) & : \omega = \sum_{i j k} f_{i j k} dx^{i} \wedge dx^{j} \wedge dx^{k}. \end {aligned}$

可以通过不断的作微分构造长正合序列（长正合序列要无限长），如图 1 所示

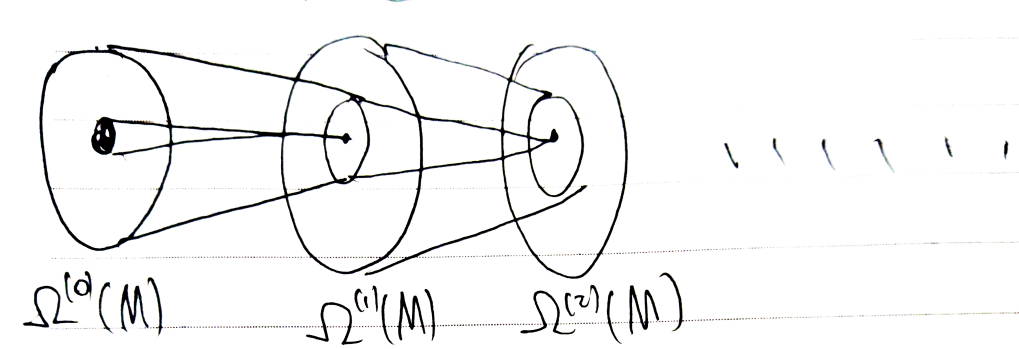
在这里插入图片描述

图 1: 不断的做微分构造长正合序列

在这里插入图片描述

图 2: 类似的可以构造短正合序列，只不过不一定用外微分来构造

$Ω0(M)→dΩ1(M)→dΩ2(M)→dΩ3(M)→d⋯→dΩn(M)→d⋯\Omega^{0}(M) \xrightarrow {d} \Omega^{1}(M) \xrightarrow {d} \Omega^{2}(M) \xrightarrow {d} \Omega^{3}(M) \xrightarrow {d} \cdots \xrightarrow {d} \Omega^{n}(M) \xrightarrow {d} \cdots$

与此对应的有短正合序列，只不过不一定用外微分构造。关于短正合序列有两个重要定理：

若 $\to A \to B \to C \to 0$ 正合，可得 $B = A$ 或 $\simeq B/C$ 。

2 用外微分推导麦克斯韦关系

其实麦克斯韦关系完全可以简化为一个公式

$dT \wedge dS = dP \wedge dV.$

下面我们可以用此方法推导其中一个麦氏关系，其它三个公式完全一摸一样的方法简便推导出来

$dT∧dS=dP∧dV⇒dT∧(∂S∂P)TdP=dP∧(∂V∂T)PdT⇒(∂S∂P)T=−(∂V∂T)P.\begin{aligned} dT\wedge dS & =dP\wedge dV \\ \Rightarrow dT\wedge {{\left( \frac{\partial S}{\partial P} \right)}_{T}}dP&=dP\wedge {{\left( \frac{\partial V}{\partial T} \right)}_{P}}dT \\ \Rightarrow {{\left( \frac{\partial S}{\partial P} \right)}_{T}}&=-{{\left( \frac{\partial V}{\partial T} \right)}_{P}}. \end{aligned}$

类似的方法推导出其它三个公式

$(∂S∂V)T=(∂P∂T)V,(∂T∂P)S=(∂V∂S)P,(∂T∂V)S=−(∂P∂S)V.\begin {aligned} \left ( \frac {\partial S}{\partial V} \right)_T &= \left ( \frac {\partial P}{\partial T} \right)_V, \\ \left ( \frac {\partial T}{\partial P} \right)_S &= \left ( \frac {\partial V}{\partial S} \right)_P, \\ \left ( \frac {\partial T}{\partial V} \right)_S &= -\left ( \frac {\partial P}{\partial S} \right)_V. \end {aligned}$

我们推导第一个式子

3 用外微分推导卡诺定理

$dH=TdS+VdP,1TdH=dS+VTdP.\begin {aligned} dH &= T dS + V dP, \\ \frac {1}{T} dH &= dS + \frac {V}{T} dP. \end {aligned}$

用外微分推导卡诺定理

$−1T2dT∧dH=0+1TdV∧dP−VT2dT∧dP,+1T2dT∧(∂H∂P)TdP=1T(∂V∂T)PdT∧dP−VT2dT∧dP,(∂H∂P)T=V−T(∂V∂T)P.\begin {aligned} -\frac {1}{T^2} dT \wedge dH &= 0 + \frac {1}{T} dV \wedge dP - \frac {V}{T^2} dT \wedge dP, \\ +\frac {1}{T^2} dT \wedge \left ( \frac {\partial H}{\partial P} \right)_T dP &= \frac {1}{T} \left ( \frac {\partial V}{\partial T} \right)_P dT \wedge dP - \frac {V}{T^2} dT \wedge dP, \\ \left ( \frac {\partial H}{\partial P} \right)_T &= V - T \left ( \frac {\partial V}{\partial T} \right)_P. \end {aligned}$

我们推导第二个式子

$dU=TdS−pdV,dS=1TdU+pTdV,ddS=0=dU∧1T2dT+1TdP∧dV+dV∧PT2dT,0=(∂U∂V)TdV∧1T2dT+1T(∂P∂T)VdT∧dV+dV∧PT2dT,(∂U∂V)T=T(∂P∂T)V−P.\begin {aligned} dU &= T dS - p dV, \\ dS &= \frac {1}{T} dU + \frac {p}{T} dV, \\ ddS &= 0 = dU \wedge \frac {1}{T^2} dT + \frac {1}{T} dP \wedge dV + dV \wedge \frac {P}{T^2} dT, \\ 0 &= \left ( \frac {\partial U}{\partial V} \right)_T dV \wedge \frac {1}{T^2} dT + \frac {1}{T} \left ( \frac {\partial P}{\partial T} \right)_V dT \wedge dV + dV \wedge \frac {P}{T^2} dT, \\ \left ( \frac {\partial U}{\partial V} \right)_T &= T \left ( \frac {\partial P}{\partial T} \right)_V - P. \end {aligned}$

3.1 外微分形式下的 Maxwell 方程组

下面我们介绍外微分形式下的 Maxwell 方程组，在此之前我们需要引入 Hodge 算子。其引入背景为：对于 1-form $A = A_x dx + A_y dy + A_z dz$ ，对其外微分可取形式为

$\left ( \frac {\partial A_y}{\partial z} - \frac {\partial A_z}{\partial y} \right) dy \wedge dz + \left ( \frac {\partial A_z}{\partial x} - \frac {\partial A_x}{\partial z} \right) dz \wedge dx + \left ( \frac {\partial A_x}{\partial y} - \frac {\partial A_y}{\partial x} \right) dx \wedge dy.$

而 $A⃗\vec {A}$ 的旋度 $∇×A⃗\nabla \times \vec {A}$ 对应的 1-form 为

$(∂Ay∂z−∂Az∂y)dx+(∂Az∂x−∂Ax∂z)dy+(∂Ax∂y−∂Ay∂x)dz.\left ( \frac {\partial A_y}{\partial z} - \frac {\partial A_z}{\partial y} \right) dx + \left ( \frac {\partial A_z}{\partial x} - \frac {\partial A_x}{\partial z} \right) dy + \left ( \frac {\partial A_x}{\partial y} - \frac {\partial A_y}{\partial x} \right) dz.$

可以看出，若我们建立映射

$dy \wedge dz \to dx, \quad dz \wedge dx \to dy, \quad dy \wedge dx \to dz,$

那么可以在 $∇×A⃗\nabla \times \vec {A}$ 与 $d A$ 之间建立对应，这也是引入 Hodge 算子的动机。更一般的，对于 n 维空间中 p 形式可用 Hodge 算子变成 (n-p) 形式

$∗(dxμ1∧dxμ2∧⋯∧dxμp)=1(n−p)!ϵνp+1⋯νnμ1⋯μpdxνp+1∧dxνp+2∧⋯∧dxνn.*(dx^{\mu_1} \wedge dx^{\mu_2} \wedge \cdots \wedge dx^{\mu_p}) = \frac {1}{(n-p)!} \epsilon_{\nu_{p+1} \cdots \nu_n}^{\mu_1 \cdots \mu_p} dx^{\nu_{p+1}} \wedge dx^{\nu_{p+2}} \wedge \cdots \wedge dx^{\nu_n}.$

其中 $ϵνp+1⋯νnμ1⋯μp\epsilon_{\nu_{p+1} \cdots \nu_n}^{\mu_1 \cdots \mu_p}$ 里面等价于 ε 符号乘了一个度量张量。

我们还可定义

$\frac {1}{2} F_{\mu \nu} dx^{\mu} \wedge dx^{\nu}.$

那么经过 Hodge 算子作用后的矩阵变为

$Fμν=[0−Ex−Ey−EzEx0Bz−ByEy−Bz0BxEzBy−Bx0],(∗F)μν=[0BxByBz−Bx0Ez−Ey−By−Ez0Ex−BzEy−Ex0].F_{\mu \nu} = \begin {bmatrix} 0 & -E_x & -E_y & -E_z \\ E_x & 0 & B_z & -B_y \\ E_y & -B_z & 0 & B_x \\ E_z & B_y & -B_x & 0 \end {bmatrix}, \quad (*F)_{\mu \nu} = \begin {bmatrix} 0 & B_x & B_y & B_z \\ -B_x & 0 & E_z & -E_y \\ -B_y & -E_z & 0 & E_x \\ -B_z & E_y & -E_x & 0 \end {bmatrix}.$

于是可以得到 Gauss 单位制下的 Maxwell 方程

$∗d∗F=4πJ,dF=0.\begin {aligned} *d*F &= 4\pi J, \\ dF &= 0. \end {aligned}$

注：温习电动力学中的叙述。

Maxwell 方程可写成如下形式

$∑μ∂μFμν=4πjν,∑νmnϵμνmn∂νFmn=0.\begin {aligned} \sum_{\mu} \partial_{\mu} F^{\mu \nu} &= 4\pi j^{\nu}, \\ \sum_{\nu m n} \epsilon_{\mu \nu m n} \partial_{\nu} F^{m n} &= 0. \end {aligned}$

讨论真空场下的能量动量张量

$Tμν=∂L∂(∂μϕ)∂νϕ−gμνL,Tμν=∂L∂(∂μAλ)∂νAλ−gμνL,L=−14FρσFρσ=−12(E2−B2).\begin {aligned} T^{\mu \nu} &= \frac {\partial L}{\partial (\partial_{\mu} \phi)} \partial^{\nu} \phi - g^{\mu \nu} L, \\ T^{\mu \nu} &= \frac {\partial L}{\partial (\partial_{\mu} A_{\lambda})} \partial^{\nu} A_{\lambda} - g^{\mu \nu} L, \\ L &= -\frac {1}{4} F_{\rho \sigma} F^{\rho \sigma} = -\frac {1}{2} (E^2 - B^2). \end {aligned}$

则可以同时得到能量动量张量

$T^μν=Tμν+∂λKλμν(Kλμν=FμλAν).\hat {T}^{\mu \nu} = T^{\mu \nu} + \partial_{\lambda} K^{\lambda \mu \nu} \quad (K^{\lambda \mu \nu} = F^{\mu \lambda} A^{\nu}).$

$ϵ=12(E2+B2),S=E×B.\epsilon = \frac {1}{2} (E^2 + B^2), \quad S = E \times B.$

3.2 猜测高维实空间情况下的 Maxwell 方程

魏贤昊猜测高维 Maxwell 方程形式依然为

$∑μ∂μFμν=4πjν,∑νmnϵμνmn∂νFmn=0.\sum_{\mu} \partial_{\mu} F^{\mu \nu} = 4\pi j^{\nu}, \quad \sum_{\nu m n} \epsilon_{\mu \nu m n} \partial_{\nu} F^{m n} = 0.$

若如此，则高维情况下电磁波解依然存在

$∑μ∂μFμν=0→∑μ∂μ∂μAν−∑ν(∑μ∂μAμ)=0.\sum_{\mu} \partial_{\mu} F^{\mu \nu} = 0 \to \sum_{\mu} \partial_{\mu} \partial^{\mu} A^{\nu} - \sum_{\nu} \left ( \sum_{\mu} \partial_{\mu} A^{\mu} \right) = 0.$

根据流守恒方程 $∂μAμ=0\partial_{\mu} A^{\mu} = 0$ 进一步得波动解

$∑μ∂μ∂μAν=0→∑μ∂μ∂μFρσ=0.\sum_{\mu} \partial_{\mu} \partial^{\mu} A^{\nu} = 0 \to \sum_{\mu} \partial_{\mu} \partial^{\mu} F^{\rho \sigma} = 0.$

可以在麦克斯韦方程基础上加上 Topo Term。当存在直流电场时，前面电场变化项可以略去，只剩余牛谦的一堆方程。

3.3 用外微分表示非阿贝尔规范场

下面我用我自己理解的方式叙述 SU (2) 规范场

$ψ→Uψ\psi \to U \psi$ , 只不过这里 $\neq \exp (-ie \vec {A} \cdot d\vec {r}$ , 即不是简单的 U (1) 规范场。SU (2) 规范场与 U (1) 规范场类似， $p^−eA^\hat {p} - e \hat {A}$ 在规范变换下不变，即

定义

$U†(∂μ−ieAμ′/ℏ)U=∂μ−ieAμ/ℏ,U^{\dagger} (\partial_{\mu} - ie A'_{\mu}/\hbar) U = \partial_{\mu} - ie A_{\mu}/\hbar,$

$(∂μ−ieAμ′/ℏ)U=U(∂μ−ieAμ/ℏ)[U†U].(\partial_{\mu} - ie A'_{\mu}/\hbar) U = U (\partial_{\mu} - ie A_{\mu}/\hbar) [U^{\dagger} U].$

$Aμ(x)→Aμ′(x)=UAμU†+iℏeU∂μU†.A_{\mu}(x) \to A'_{\mu}(x) = U A_{\mu} U^{\dagger} + \frac {i \hbar}{e} U \partial_{\mu} U^{\dagger}.$

$Dμ=∂μ−ieAμ/ℏ,Dμ′=∂μ−ieAμ′/ℏ,UDμU†=UDμ′U†.\begin {aligned} D_{\mu} &= \partial_{\mu} - ie A_{\mu}/\hbar, \\ D'_{\mu} &= \partial_{\mu} - ie A'_{\mu}/\hbar, \\ U D_{\mu} U^{\dagger} &= U D'_{\mu} U^{\dagger}. \end {aligned}$

$Fμν′=Dμ′Aν′−Dν′Aμ′=∂μAν′−∂νAμ′−ieℏ[Aμ′,Aν′],Fμν′=∂μ(UAνU†+iℏeU∂νU†)−∂ν(UAμU†+iℏeU∂μU†)−ieℏ[UAμU†+iℏeU∂μU†][UAνU†+iℏeU∂νU†]+ieℏ[UAνU†+iℏeU∂νU†][UAμU†+iℏeU∂μU†]=U(∂μAν−∂νAμ−ieℏ[Aμ,Aν])U†=U(DμAν−DνAμ)U†.\begin {aligned} F'_{\mu \nu} &= D'_{\mu} A'_{\nu} - D'_{\nu} A'_{\mu} = \partial_{\mu} A'_{\nu} - \partial_{\nu} A'_{\mu} - i \frac {e}{\hbar} [A'_{\mu}, A'_{\nu}], \\ F'_{\mu \nu} &= \partial_{\mu} (U A_{\nu} U^{\dagger} + \frac {i \hbar}{e} U \partial_{\nu} U^{\dagger}) - \partial_{\nu} (U A_{\mu} U^{\dagger} + \frac {i \hbar}{e} U \partial_{\mu} U^{\dagger}) \\ &\quad - \frac {i e}{\hbar} [U A_{\mu} U^{\dagger} + \frac {i \hbar}{e} U \partial_{\mu} U^{\dagger}][U A_{\nu} U^{\dagger} + \frac {i \hbar}{e} U \partial_{\nu} U^{\dagger}] \\ &\quad + \frac {i e}{\hbar} [U A_{\nu} U^{\dagger} + \frac {i \hbar}{e} U \partial_{\nu} U^{\dagger}][U A_{\mu} U^{\dagger} + \frac {i \hbar}{e} U \partial_{\mu} U^{\dagger}] \\ &= U (\partial_{\mu} A_{\nu} - \partial_{\nu} A_{\mu} - i \frac {e}{\hbar} [A_{\mu}, A_{\nu}]) U^{\dagger} \\ &= U (D_{\mu} A_{\nu} - D_{\nu} A_{\mu}) U^{\dagger}. \end {aligned}$

由于 $∂μU=−U(∂μU†)U\partial_{\mu} U = -U (\partial_{\mu} U^{\dagger}) U$ 和 $∂μU†=−U†(∂μU)U†\partial_{\mu} U^{\dagger} = -U^{\dagger} (\partial_{\mu} U) U^{\dagger}$ ，可将上式化简为

$Fμν′=UFμνU†.F'_{\mu \nu} = U F_{\mu \nu} U^{\dagger}.$

定义 $\exp (-i \theta^a T^a)$ ，要求 $[Ta,Tb]=ϵabcTc[T^a, T^b] = \epsilon_{abc} T^c$ 。在 SU (2) 规范场中

$Ta=σa2,Aμ=∑cAμcTc,Fμν=∑cFμνcTc.T^a = \frac {\sigma^a}{2}, \quad A_{\mu} = \sum_{c} A_{\mu}^{c} T^{c}, \quad F_{\mu \nu} = \sum_{c} F_{\mu \nu}^{c} T^{c}.$

可得

$Aμ′a=Aμa+ϵabcθbAμc−∂μθa,Fμν′a=∂μAνa−∂νAμa+eℏϵabcAμbAνc.\begin{aligned} A'_{\mu}{}^{a} &= A_{\mu}{}^{a} + \epsilon_{abc} \, \theta^{b} A_{\mu}{}^{c} - \partial_{\mu} \theta^{a}, \\ F'_{\mu \nu}{}^{a} &= \partial_{\mu} A_{\nu}{}^{a} - \partial_{\nu} A_{\mu}{}^{a} + \frac{e}{\hbar} \epsilon_{abc} A_{\mu}{}^{b} A_{\nu}{}^{c}. \end{aligned}$

我们常常应用时间规范下的形式，即规范势的时空分量为 0（即不考虑含时演化）形式，有

$A0(x)=0,Ai≠0(x)=iℏeU∂iU†,∂μ=∂μ.A_{0}(x) = 0, \quad A_{i \neq 0}(x) = \frac {i \hbar}{e} U \partial_{i} U^{\dagger}, \quad \partial_{\mu} = \partial^{\mu}.$

4 用外微分计算高维空间的拓扑不变量

4.1

举一个例子，物理学中几何相计算公式为

$γ=−Im∬dkxdky(<∂ψ∂kx∣∂ψ∂ky>−<∂ψ∂ky∣∂ψ∂kx>).\gamma = -\text {Im} \iint dk_x dk_y \left ( \left< \frac {\partial \psi}{\partial k_x} \bigg| \frac {\partial \psi}{\partial k_y} \right> - \left< \frac {\partial \psi}{\partial k_y} \bigg| \frac {\partial \psi}{\partial k_x} \right> \right).$

如果我们把 $dk_x$ 和 $dk_y$ 做对换，若 $dkx⋅dky=dky⋅dkxdk_x \cdot dk_y = dk_y \cdot dk_x$ ，那么得到几何相永远为零，这显然是荒谬的。因此正确形式应为 $dkx∧dkydk_x \wedge dk_y$ ，满足如下形式

$dkx∧dky=−dky∧dkx.dk_x \wedge dk_y = -dk_y \wedge dk_x.$

在多变量微积分中常常一不讲外微分，二是学生普遍对 $dk_x dk_y = -dk_y dk_x$ 缺乏了解，故真正在计算积分时会发生类似这类荒谬的错误。因此我强烈建议多变量微积分中不要省略外微分符号。

4.2 外微分表示高维空间拓扑不变量

在我本科毕业论文第二章系统证明了 2D 和 3D 拓扑不变量的计算公式为

$h^(k)=h⃗(k)∣h⃗(k)∣,\hat {h}(k) = \frac {\vec {h}(k)}{|\vec {h}(k)|},$

$C1D=−12π∫∂V∂kh^(k)⋅h^(k),C_{1D} = -\frac {1}{2\pi} \int_{\partial V} \partial_k \hat {h}(k) \cdot \hat {h}(k),$

$C2D=−14π∫∂V[∂kxh^(k)×∂kyh^(k)]⋅h^(k).C_{2D} = -\frac {1}{4\pi} \int_{\partial V} \left [ \partial_{k_x} \hat {h}(k) \times \partial_{k_y} \hat {h}(k) \right] \cdot \hat {h}(k).$

其中 V 为所有矢量 $h^(k)\hat {h}(k)$ 围成的球。写成外微分形式得

$C1D=−12π∫∂Vϵimdh^i(k)⋅h^m(k),C_{1D} = -\frac {1}{2\pi} \int_{\partial V} \epsilon^{im} d\hat {h}_i (k) \cdot \hat {h}_m (k),$

$C2D=−14π∫∂Vϵimn(dh^i(k)∧dh^m(k))⋅h^n(k).C_{2D} = -\frac {1}{4\pi} \int_{\partial V} \epsilon^{imn} (d\hat {h}_i (k) \wedge d\hat {h}_m (k)) \cdot \hat {h}_n (k).$

注意到

$43π=∫V′ϵimn13!dk^i∧dk^m∧dk^n,\frac {4}{3}\pi = \int_{V'} \epsilon^{imn} \frac {1}{3!} d\hat {k}_i \wedge d\hat {k}_m \wedge d\hat {k}_n,$

其中 $V^{'}$ 为 $∣k^∣=1|\hat {k}| = 1$ 围成的球体积。因此我们可以借机推广到 n 维球体积公式为

$CnD=−∫∂Vϵi1⋯in(dh^i1(k)∧⋯∧dh^in−1(k))⋅h^in(k)∫V′ϵi1⋯indki1∧⋯∧dkin×(n−1)!.C_{nD} = -\frac { \int_{\partial V} \epsilon^{i_1 \cdots i_n} (d\hat {h}_{i_1}(k) \wedge \cdots \wedge d\hat {h}_{i_{n-1}}(k)) \cdot \hat {h}_{i_n}(k) }{ \int_{V'} \epsilon^{i_1 \cdots i_n} dk_{i_1} \wedge \cdots \wedge dk_{i_n} } \times (n-1)!.$

由 S4 球面表面积为 $8π23R4\frac {8\pi^2}{3} R^4$ ，可求出 $n = 4$ 情形为

$C4D=−38π2∫d4kϵabcded^a∂xd^b∂yd^c∂zd^d∂wd^e.C_{4D} = -\frac {3}{8\pi^2} \int d^4 k \epsilon^{abcde} \hat {d}_a \partial_x \hat {d}_b \partial_y \hat {d}_c \partial_z \hat {d}_d \partial_w \hat {d}_e.$

参考文献

常庚哲，史济怀，《数学分析（第二册）》
《热力学与统计物理》，汪志诚著
http://home.ustc.edu.cn/lxsphys/index.html
《微积分五讲》，龚著
《Introduction to Quantum Field Theory》，Peskin
《Quantum Field Theory in a nutshell》，A. Zee
《量子力学的前沿问题》，张礼，葛墨林等著，第二版
https://zhuanlan.zhihu.com/p/46544376

via:

如何通俗易懂地解释外微分？ - 知乎
https://www.zhihu.com/question/263674338
外微分究竟为什么是可行的？ - 知乎
https://www.zhihu.com/question/521663115
外微分：简化多变量微积分中的公式、简化热统中公式、简化非阿贝尔规范场的表述.pdf
http://home.ustc.edu.cn/~weixianhao/beyond/waiweifen.pdf

查看全文

http://www.lryc.cn/news/615508.html