第十四届蓝桥杯青少年组省赛 编程题真题题解
明天我就要考蓝桥杯省赛了,本蒟蒻已瑟瑟发抖,所以现在写一篇文章。
题目分别为:
1.B4270 [蓝桥杯青少年组省赛 2023] 特殊运算符
2.B4271 [蓝桥杯青少年组省赛 2023] 四叶玫瑰数
3.B4272 [蓝桥杯青少年组省赛 2023] 质因数的个数
4.B4273 [蓝桥杯青少年组省赛 2023] 最大的矩形纸片
……(本人只讲解前四道题,后两道是蓝题,不会做了)
题解开始:
第一题:
题目描述
假定有一个运算符 >>>,它的功能如下所示:
>>> 257=25>>> 182=18>>> 933=93
给定一个正整数 N(100<N<1000),请计算 N−(>>> N) 的结果。
例如:N=257 时,257−(>>> 257)=257−25=232。
输入格式
输入一个正整数 N(100<N<1000)。
输出格式
输出一个整数,表示 N−(>>> N) 的结果
输入输出样例
输入 #1复制
257
输出 #1复制
232
这道题十分简单,这里不多说,直接上AC代码:
#include<bits/stdc++.h>
using namespace std;
int n;
int main(){cin>>n;cout<<n-(n/100*10+n/10%10);return 0;
}时间复杂度:O(1)
第二题:
题目描述
四叶玫瑰数是指一个四位数,其各位上的数字的四次方之和等于本身。
给定两个正整数 N 和 M ,请将 N∼M(1≤N≤M≤1000000) 之间(含 N 和 M)的四叶玫瑰数按从小到大的顺序输出。
例如:N=1234,M=2345 时,有一个四叶玫瑰数 1634,因为 14+64+34+44=1634,故输出 1634。
输入格式
第一行输入两个正整数 N,M(1≤N≤M≤1000000)。
输出格式
输出一行,包含若干个用一个空格隔开的正整数,表示 N∼M 之间的四叶玫瑰数按从小到大的顺序的输出结果。
题目数据保证给定的 N∼M 范围内至少有一个四叶玫瑰数
输入输出样例
输入 #1复制
1234 2345
输出 #1复制
1634
这道题照样简单,先写一个for循环,从N开始到M结束。每一次for循环,都求出各个数位的4次方之和,最后判断一下是否等于i就行了。上AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,m;
int main(){cin>>n>>m;int sum=0;for(int i=n;i<=m;i++){if(i<=999||i>9999) continue;int t=i;sum=pow(i/1000,4)+pow(i/100%10,4)+pow(i/10%10,4)+pow(i%10,4);if(sum==t) cout<<sum<<' ';}return 0;
}时间复杂度:O(m-n)
第三题:
题目背景
- 因数:又称为约数,如果整数 a 除以整数 b(b=0) 的商正好是整数而没有余数,我们就说 b 是 a 的因数。
- 质数:又称为素数,一个大于 1 的自然数,除了 1 和它自身外,不能被其他自然数整除的数叫做质数。2 是最小的质数。
- 质因数:如果一个数 a 的因数 b 同时也是质数,那么 b 就是 a 的一个质因数,例如:8=2×2×2,2 就是 8 的质因数;12=2×2×3,2 和 3 就是 12 的质因数。
题目描述
给定两个正整数 N 和 M(1≤N≤M≤107),统计 N 到 M 之间(含 N 和 M)每个数所包含的质因数的个数,输出其中最大的个数。
例如: 当 N=6,M=10,6 到 10 之间:
- 6 的质因数是 2,3,共有 2 个;
- 7 的质因数是 7,共有 1 个;
- 8 的质因数是 2,2,2,共有 3 个;
- 9 的质因数是 3,3,共有 2 个;
- 10 的质因数是 2,5,共有 2 个;
6 到 10 之间的数中质因数最多的是 8,质因数有 3 个,故输出 3。
输入格式
输入两个正整数 N 和 M(1≤N≤M≤107),两个正整数之间用一个空格隔开。
输出格式
输出一个整数,表示质因数个数中的最大值。
输入输出样例
输入 #1复制
6 10
输出 #1复制
3
这道题有两种做法:
第一种:暴力
代码:
#include<bits/stdc++.h>
using namespace std;
vector<int> gp(int x){vector<bool> p(x+1,true);p[0]=p[1]=false;for(int i=2;i<=sqrt(x);i++){if(p[i]){for(int j=i*i;j<=x;j+=i){p[j]=false;}}}vector<int> pp;for(int i=2;i<=x;i++){if(p[i]){pp.push_back(i);}}return pp;
}
int zys(int num,const vector<int>& pp){int cnt=0;for(int p:pp){if(p*p>num) break;if(num%p==0){while(num%p==0){num/=p;cnt++;}}}if(num>1){cnt++;}return cnt;
}
int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int n,m;cin>>n>>m;vector<int> ppp=gp(m);int maxx=0;for(int i=n;i<=m;i++){int c=zys(i,ppp);if(c>maxx){maxx=c;}}cout<<maxx;return 0;
}但是只得90分,要想进入国赛,这道题必须拿下(除非你会做后面3题)。所以:
第二种做法:DP优化
代码:
#include<bits/stdc++.h>
using namespace std;
int n,m,dp[10000005],ans=0;
bool vis[10000005];
int main(void){cin>>n>>m;for(int i=2;i<=m;i++){if(vis[i]) continue;dp[i]=1;for(int j=2;j<=m/i;j++){vis[i*j]=true;dp[i*j]=dp[j]+1;}}for(int i=n;i<=m;i++){ans=max(ans,dp[i]);}cout<<ans;return 0;
}时间复杂度:O(m log m)
第四题:
题目描述
一张半边参差不齐的网格纸(网格边长均为 1),有一边是完整没有破损的。现要从中剪出一片面积最大的矩形纸片。
给定网格纸中完整边的长度 N(1≤N≤1000000),以及网格中每一列残存部分的高度(1≤ 高度 ≤10000),输出能够剪出的最大矩形纸片面积。
输入格式
第一行输入一个正整数 N(1≤N≤1000000),表示纸片完整边的长度。
第二行输入 N 个正整数(1≤ 正整数 ≤10000),表示每列格子残存部分的高度,两个正整数之间用一个空格隔开。
输出格式
输出一个正整数,表示能够剪出的最大矩形纸片面积。
输入输出样例
输入 #1复制
6 3 2 1 4 5 2
输出 #1复制
8
先读题,给定 n 个宽为 1 的矩形,每个矩形的高各不相同。将它们拼在一起,要求在从中剪出一块最大的矩形纸片。
我们很自然可以想到枚举左右起始位置,在枚举中间的位置来计算当前区间内的最大矩形长度,再来更新答案。
#include<bits/stdc++.h>
using namespace std;
int h[1000001];
int main(){int n;cin>>n;for(int i=1;i<=n;i++){cin>>h[i];}int maxn=0;for(int i=1;i<=n;i++){int m=1e9+1;for(int j=i;j<=n;j++){for(int k=i;k<=j;k++){m=min(m,h[k]);} maxn=max(maxn,m*(j-i+1));}}cout<<maxn<<endl;return 0;
}
结果……30 分
我们可以发现该解法的时间复杂度为 O(n3)。 所以我们得换一种方法来写。 我们可以先假设矩形长度递增,那么我们该如何做?
很显然,我们可以尝试将当前的矩形的高度作为最后矩形的高度,并将该矩形的宽一直延伸到右边界,再算出矩形的面积用来更新答案。
所以我们看回这道题,我们可以利用上面的结论,如果下一个矩形的高度比上一个小,那么该矩形想与前面的矩形拼成一个更大的矩形,那么之前的矩形高于当前矩形的面积就没有任何用处了(如下图中打叉的部分)。
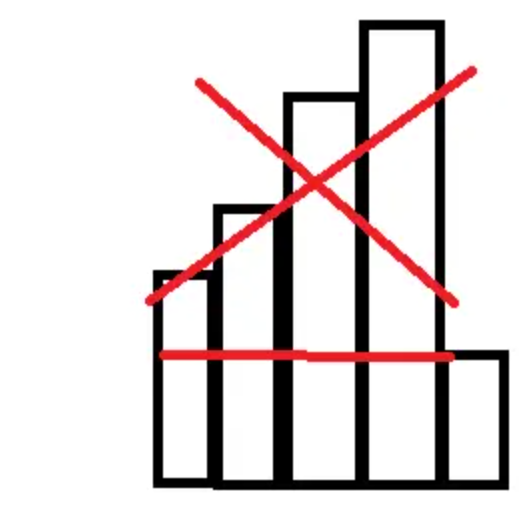
所以我们就可以用到一种算法来解决这种问题————单调栈。
我们只需要建立一个栈,用来维护一个高度始终单调的序列,这样我们就可以解决这个问题了。
我们先从左到右依次扫描每个矩形,如果当前的矩形高度高于栈顶矩形,就让其进栈;否则就不断取出栈顶,直至栈为空或栈顶矩形的高度比当前矩形小。出栈过程中我们累加弹出矩形的宽度,并且在每次弹出时,就用其高度乘以累加的宽度去更新答案。出栈结束后,我们再把一个高度为当前矩形高度、宽度为累加值的矩形入栈。注意,结束后,要将栈中剩下的矩形依次弹出,采用上面相同的方法来更新答案。所以我们可以增加一个高度为 0 的矩形,避免再扫描结束后有剩余矩形。
AC代码1——数组模拟:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int a[1000001];
int s[1000001];
int w[1000001];
int n;
signed main(){int p=0,ans=0;cin>>n;for(int i=1;i<=n;i++) cin>>a[i]; a[n+1]=0; for(int i=1;i<=n+1;i++){if(a[i]>s[p]){s[++p]=a[i];w[p]=1;}else{int width=0;while(s[p]>a[i]){width+=w[p];ans=max(ans,(long long)width*s[p]);p--;}s[++p]=a[i];w[p]=width+1;}}cout<<ans<<endl;return 0;
}
AC代码2——STL:
#include<bits/stdc++.h>
using namespace std;
struct node{int h,w;
};
stack<node>s;
long long a[1000001];
long long ans=0;
int main(){int n;cin>>n;for(int i=1;i<=n;i++) cin>>a[i];a[n+1]=0;for(int i=1;i<=n+1;i++){long long width=0;while(!s.empty() && a[i]<s.top().h){//单调递增width=width+s.top().w;ans=max(ans,width*s.top().h);s.pop();}s.push( (node){a[i],width+1} );}cout<<ans<<endl;return 0;
}
好了宝子们,今天的题解就到这里,我们明天再会!
制作不易,点个关注再走叭!
