[Python]代码随想录Day35[动态规划][背包问题]
01背包问题 二维
01背包:有n种物品, 每种物品只有一个
完全背包:有n种物品,每种物品有无限个
多重背包:有n种物品,每种物品的个数各不相同
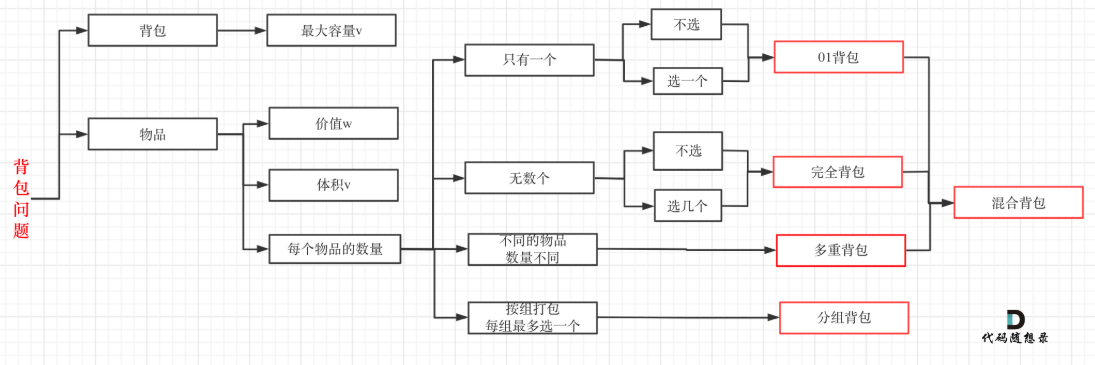
eg:
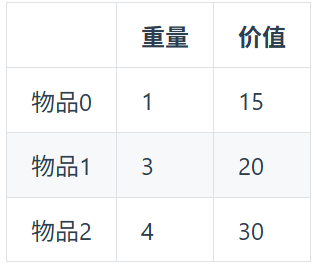
背包的重量为4,装满这个背包的最大价值是什么?
暴力解法:
每个物品取或者不取 O(n^2) 回溯
有二维dp数组解法是基础,在这个基础上需要优化成一维dp数组
01背包解法:
1.dp数组的定义 含义
dp[i][j] 下标[0-1]之间的物品任取 然后放进容量为j的背包里 的价值
dp[i][j]
不放物品i 的最大价值dp[i - 1][j]
放物品i dp[i - 1][j - weight(i)] + value(i)
不选:在剩余容量为c时,从前i- 1个物品中得到的最大价值和
选: 在剩余容量我c - weight(i)时,从前i - 1个物品中得到的最大价值之和
2.递推公式dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight(i)] + value(i))
3.初始化dp数组
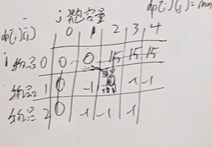
4.遍历顺序
5.打印
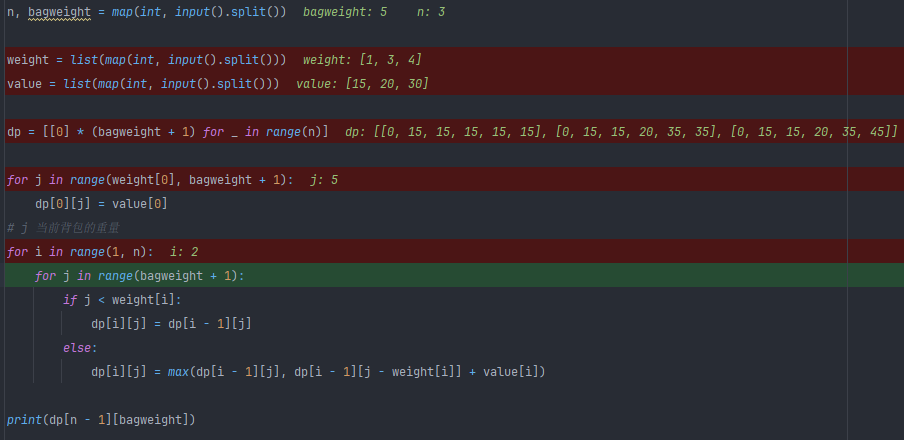
n, bagweight = map(int, input().split())weight = list(map(int, input().split()))
value = list(map(int, input().split()))dp = [[0] * (bagweight + 1) for _ in range(n)]for j in range(weight[0], bagweight + 1):dp[0][j] = value[0]
# j 当前背包的重量
for i in range(1, n):for j in range(bagweight + 1):if j < weight[i]:dp[i][j] = dp[i - 1][j]else:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])print(dp[n - 1][bagweight])输入中map是用来转换数据类型的
map(int, ['1', '3', '4', '2'])
它的作用是把 int() 这个函数应用到列表中的每个元素,就像:
[int('1'), int('3'), int('4'), int('2')] → [1, 3, 4, 2]
input进来“1 3 5”
经过split变成["1","3","5"]
再进过map变成map的object,
在经过list变成[1,3,5]
01背包问题 一维(滚动数组)
1.dp数组的定义 含义
dp[j] 容量为j的背包 所能装的最大价值为dp[j]
2.递推公式
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight(i)] + value(i))
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
dp[j] 把上一层物品的数据拷贝下来了
3.初始化dp数组
dp[0] = 0
4. 遍历顺序 逆序遍历
n = 3, bagweight = 5
weight = [1, 3, 4]
value = [15, 20, 30]
初始化
dp = [0, 0, 0, 0, 0, 0] # 下标代表容量 0...5
处理物品 i=0(重1,价15)
外层 i=0;内层 j 从 5 → 1 递减:
j=5: dp[5] = max(dp[5], dp[4]+15) = max(0, 0+15)=15
j=4: dp[4] = max(dp[4], dp[3]+15) = 15
j=3: dp[3] = max(dp[3], dp[2]+15) = 15
j=2: dp[2] = max(dp[2], dp[1]+15) = 15
j=1: dp[1] = max(dp[1], dp[0]+15) = 15
结果:
dp = [0, 15, 15, 15, 15, 15]
处理物品 i=1(重3,价20)
外层 i=1;内层 j 从 5 → 3:
j=5: dp[5] = max(dp[5], dp[2]+20) = max(15, 15+20)=35
j=4: dp[4] = max(dp[4], dp[1]+20) = max(15, 15+20)=35 → 但容量4装不下“1+3”同时吗?
装得下:1(重1)来自 dp[1]=15,再加当前物品(重3)共重4,值35 ✅
j=3: dp[3] = max(dp[3], dp[0]+20) = max(15, 0+20)=20
结果(处理完第2件后):
dp = [0, 15, 15, 20, 35, 35]
处理物品 i=2(重4,价30)
外层 i=2;内层 j 从 5 → 4:
j=5: dp[5] = max(dp[5], dp[1]+30) = max(35, 15+30)=45 → 选第0(重1,15) + 第2(重4,30) = 总重5,总值45
j=4: dp[4] = max(dp[4], dp[0]+30) = max(35, 0+30)=35 → 不变(容量4:放第2件价值30,其实比上一轮临时的35低,但上一轮的35来自“第0+第1”的组合,确实可行,所以保持35)
最终:
dp = [0, 15, 15, 20, 35, 45]
输出
print(dp[bagweight]) -> dp[5] = 45
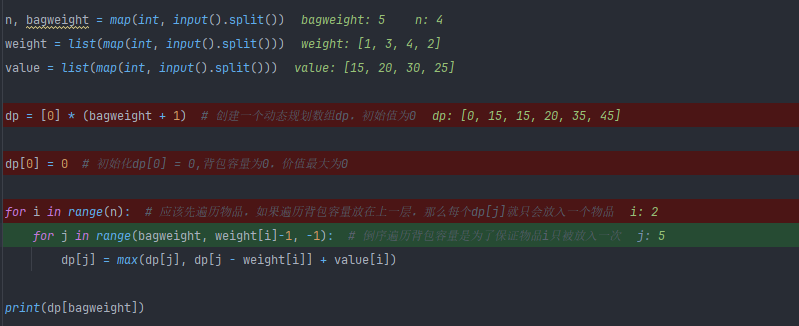
n, bagweight = map(int, input().split())
weight = list(map(int, input().split()))
value = list(map(int, input().split()))dp = [0] * (bagweight + 1) # 创建一个动态规划数组dp,初始值为0dp[0] = 0 # 初始化dp[0] = 0,背包容量为0,价值最大为0for i in range(n): # 应该先遍历物品,如果遍历背包容量放在上一层,那么每个dp[j]就只会放入一个物品for j in range(bagweight, weight[i]-1, -1): # 倒序遍历背包容量是为了保证物品i只被放入一次dp[j] = max(dp[j], dp[j - weight[i]] + value[i])print(dp[bagweight])
416. 分割等和子集

哪些元素相加等于数组之和的一半
容量为11的背包能不能装满一个数组
1.dp含义
dp[j] 容量为j的背包,所背的最大价值为dp[j]
重点等于价值
target = nums.sum()/2
dp[target] = target
2.递推公式
dp[j] = max(dp[j], dp[j - weight[i] + value[i])
这里压缩是因为如果i表示物体索引,由于i从小到大遍历,那么本次dp[j]的值是由上次i-1得到的
dp[j] = max(dp[j],dp[j - nums[i]] + nums[i])
3.初始化
dp[0] = 0
4.遍历顺序
for i in len(len(nums)):
for j in range(target, num[i] - 1, -1):
5.打印
class Solution:def canPartition(self, nums: List[int]) -> bool:if sum(nums) % 2 != 0:return Falsetarget = sum(nums) // 2dp = [0] * (target + 1)for num in nums:for j in range(target,num - 1, -1):dp[j] = max(dp[j], dp[j - num] + num)return dp[-1] == target
