【数据结构——并查集】
引入
并查集(Disjoint Set Union,DSU)是一种用于管理元素分组的数据结构。
合并(Union):将两个不相交的集合合并为一个集合。
查找(Find):确定某个元素属于哪个集合,通常通过返回集合的“代表元素”(groupID或父节点)实现。
quickFind 和 quickUnion 是并查集的两种实现方式。
每个元素初始时是一个独立的集合,其groupID是本身下标或父节点指向自己(分别表明各自属于哪个集合)。
如下:
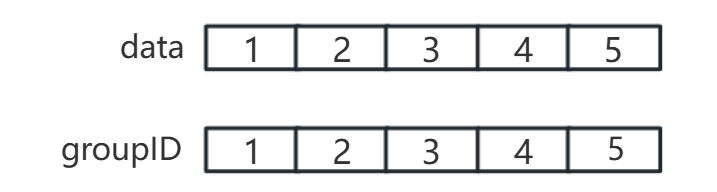
主要就是对两个数组所存的内容进行操作,特别是代表元素部分。
对代表元素进行操作的方向(思考角度)不同,就会使用不同的解决方案(如选择quickFind还是quickUnion,)
quickFind
每个元素直接指向其所属集合的代表元(根节点),合并操作时需要遍历整个数组更新所有相关元素。
时间复杂度:
查找(Find):O(1),直接访问数组即可确定所属集合。
合并(Union):O(n),需要遍历数组更新所有属于同一集合的元素。
特点:查找速度快,但合并效率低(找快合慢)。

quickUnion
使用树结构表示集合(看下图只能体现链,后面的内容会讲到路径压缩:通过增大节点的度来提高效率进而体现出树的特点),每个元素指向其父节点,根节点指向自身(下图中未标)。合并时只需将一个树的根指向另一个树的根就能连接两个集合。
时间复杂度:
查找(Find):O(logn)(平均,取决于树高),需要递归或迭代找到根节点。
合并(Union):O(logn),仅需修改根节点的指向。
特点:合并效率高,但查找速度取决于树高。可通过路径压缩等进一步提升性能(之后的内容会讲到)。

合并的方案有多种,这里仅展示其中一种。
大致思路捋顺之后就开始敲了~
//////////////下集预告//////////////
