机器学习核心算法与实践要素(全篇)
目录
一、学习分类
监督学习
半监督学习
无监督学习
强化学习
二、sklearn工具
玩具数据集加载
现实世界数据集加载(联网)
三、数据集划分
列表数据集划分
ndarray数据集划分
二维数组数据集划分
DataFrame数据集划分
字典数据集划分
鸢尾花数据集划分
现实世界数据集划分
四、特征工程
稀疏矩阵
非稀疏矩阵(稠密矩阵)
DcitVectorizer字典列表特征提取
CountVectorizer文本特征提取
TfidfVectorizer TF-IDF文本特征提取词
五、无量纲化-预处理
MinMaxScaler归一化
normalize归一化
<1> L1归一化
<2> L2归一化
<3> max归一化
StandardScaler标准化
六、特征降维
特征选择
VarianceThreshold 低方差过滤特征选择
相关系数特征选择
主成分分析
七、KNN算法
样本距离判断
(1)欧氏距离
(2)曼哈顿距离
KNN算法
原理
缺点
模型保存与加载
八、模型选择和调优
交叉验证
保留交叉验证HoldOut
K-折交叉验证(K-fold)
分层l-折交叉验证(Stratified k-fold)
其他验证
去除p交叉验证
留一交叉验证
蒙特卡罗交叉验证
时间序列交叉验证
超参数搜索
九、朴素贝叶斯分类
贝叶斯思想
贝叶斯推断
朴素贝叶斯推断
拉普拉斯平滑系数
十、决策树分类
基于信息增益决策树的建立
信息熵
信息增益
信息增益决策树建立步骤
基于基尼指数决策树建立
十一、集成学习之随机森林
十二、线性回归
线性回归
损失函数
多参数回归
最小二乘法
梯度下降
学习率
自己实现梯度下降
sklearn梯度下降
批量梯度下降BGD
随机梯度下降SGD
小批量梯度下降MBGD
欠拟合和过拟合
欠拟合
过拟合
正则化
岭回归Ridge
拉索回归Lasso
十三、逻辑回归
概念
原理
十四、无监督之K-Means算法
无监督学习
K-means算法
总结
一、学习分类
监督学习
监督学习(Supervised Learning)是从有标签的训练数据中学习模型,然后对某个给定的新数据利用模型预测它的标签。如果分类标签精确度越高,则学习模型准确度越高,预测结果越精确。
监督学习主要用于回归和分类。
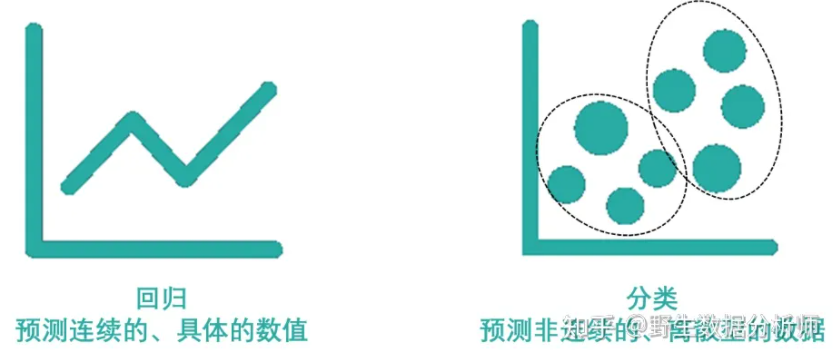
常见的监督学习的回归算法有线性回归、回归树、K邻近、Adaboost、神经网络等。
常见的监督学习的分类算法有朴素贝叶斯、决策树、SVM、逻辑回归、K邻近、Adaboost、神经网络等。
半监督学习
半监督学习(Semi-Supervised Learning)是利用少量标注数据和大量无标注数据进行学习的模式。
半监督学习侧重于在有监督的分类算法中加入无标记样本来实现半监督分类。
常见的半监督学习算法有Pseudo-Label、Π-Model、Temporal Ensembling、Mean Teacher、VAT、UDA、MixMatch、ReMixMatch、FixMatch等。
无监督学习
无监督学习(Unsupervised Learning)是从未标注数据中寻找隐含结构的过程。
无监督学习主要用于关联分析、聚类和降维。
常见的无监督学习算法有稀疏自编码(Sparse Auto-Encoder)、主成分分析(Principal Component Analysis, PCA)、K-Means算法(K均值算法)、DBSCAN算法(Density-Based Spatial Clustering of Applications with Noise)、最大期望算法(Expectation-Maximization algorithm, EM)等。
强化学习
强化学习(Reinforcement Learning)类似于监督学习,但未使用样本数据进行训练,是是通过不断试错进行学习的模式。
在强化学习中,有两个可以进行交互的对象:智能体(Agnet)和环境(Environment),还有四个核心要素:策略(Policy)、回报函数(收益信号,Reward Function)、价值函数(Value Function)和环境模型(Environment Model),其中环境模型是可选的。
强化学习常用于机器人避障、棋牌类游戏、广告和推荐等应用场景中。
二、sklearn工具

1.Python语言机器学习工具
2.Scikit-learn包括许多智能的机器学习算法的实现
3.Scikit-learn文档完善,容易上手,丰富的API接口函数
4.Scikit-learn官网:4.https://scikit-learn.org/stable/#
5.Scikit-learn中文文档:https://scikitlearn.com.cn/
scikit-learn的安装( 进入到对应虚拟环境后再下载,下载速度慢可加入-i及以后的代码作为加速源 )
pip install scikit -i https://pypi.tuna.tsinghua.edu.cn/simplescikit-learn包含的内容有:
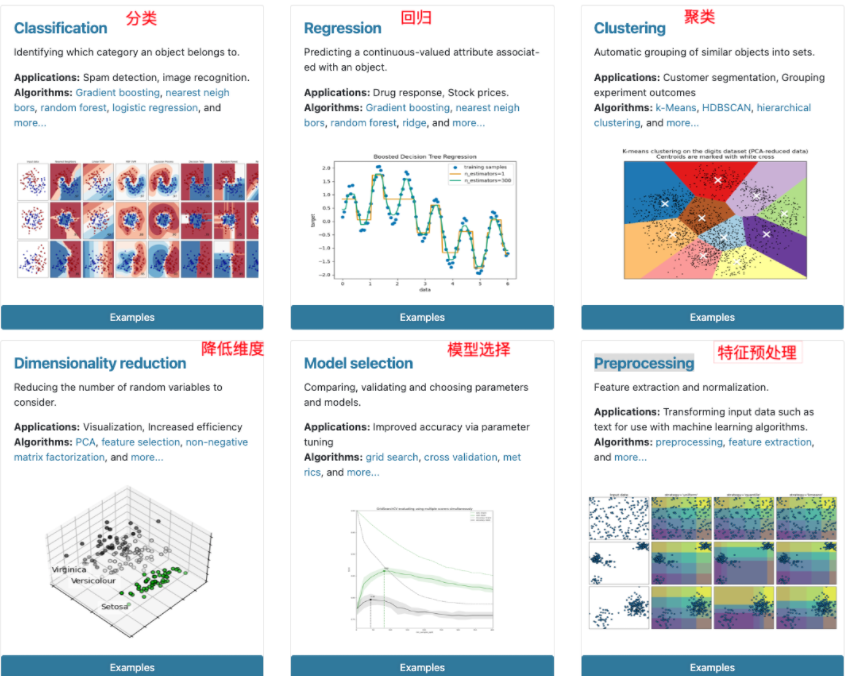
玩具数据集加载
数据量小,且保存在sklearn库本地,不用联网也可获取
from sklearn.datasets import load_iris(选择导入的数据集,如iris鸢尾花)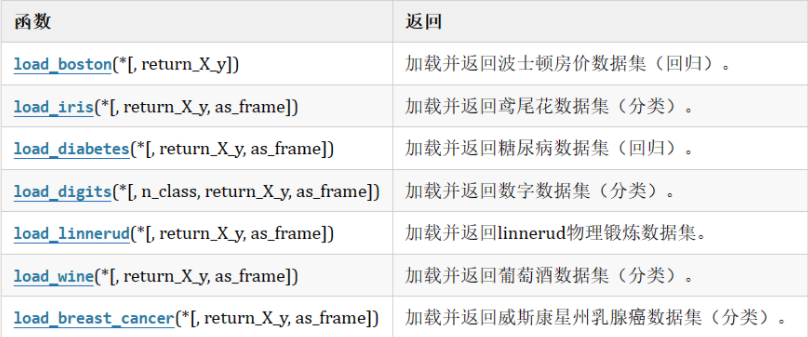
现实世界数据集加载(联网)
数据量大,只能通过联网获取
from sklearn.datasets import fetch_20newsgroups(联网加载20newsgroups数据集,从公开数据集下载)
三、数据集划分
列表数据集划分
from sklearn.model_selection import train_test_split
data1 = [1, 2, 3, 4, 5]
data2 = ["1a", "2a","3a", "4a", "5a"]
# 对数据集进行划分,测试集占比40%,则训练集60%,随机种子保证每次选取数据一致,无种子则随机
a, b = train_test_split(data1, test_size=0.4, random_state=22)
print(a, b) #[4, 1, 5] [2, 3]a, b = train_test_split(data2, test_size=0.4, random_state=22)
print(a, b) #['4a', '1a', '5a'] ['2a', '3a']a, b, c, d = train_test_split(data1, data2, test_size=0.4, random_state=22)
print(a,b,c,d) #['4a', '1a', '5a'] ['2a', '3a']ndarray数据集划分
划分前和划分后的数据类型是相同的
data1为list,划分后的a、b也是list
data2为ndarray,划分后的c、d也是ndarray
from sklearn.model_selection import train_test_split
import numpy as np
data1 = [1, 2, 3, 4, 5]
data2 = np.array(["1a", "2a","3a", "4a", "5a"]) a, b, c, d = train_test_split(data1, data2, test_size=0.4, random_state=22)print(a, b, c, d) #[4, 1, 5] [2, 3] ['4a' '1a' '5a'] ['2a' '3a']print(type(a), type(b), type(c), type(d))
#<class 'list'> <class 'list'> <class 'numpy.ndarray'> <class 'numpy.ndarray'>二维数组数据集划分
train_test_split只划分第一维度,第二维度保持不变
from sklearn.model_selection import train_test_split
import numpy as np
data1 = np.arange(1, 16, 1) #创建1-16的数组(不包含16,左闭右开),步长为1
data1.shape=(5,3) # 5行3列的数组
print(data1)
a, b = train_test_split(data1, test_size=0.4, random_state=22) #划分数据集
print("a=\n", a)
# [[10 11 12]
# [ 1 2 3]
# [13 14 15]]
print("b=\n", b)
# [[4 5 6]
# [7 8 9]]DataFrame数据集划分
from sklearn.model_selection import train_test_split
import numpy as np
import pandas as pddata1 = np.arange(1, 16, 1)
data1.shape=(5,3)
# 转换为DataFrame,指定索引和列名
data1 = pd.DataFrame(data1, index=[1,2,3,4,5], columns=["one","two","three"])
print(data1)a, b = train_test_split(data1, test_size=0.4, random_state=22)
print("\n", a)
print("\n", b)
字典数据集划分
from sklearn.feature_extraction import DictVectorizer
data = [{'city':'成都', 'age':30, 'temperature':20},{'city':'北京', 'age':42, 'temperature':80},{'city':'上海', 'age':22, 'temperature':70},]
# 创建转换器实例 True稀疏矩阵 False稠密矩阵
transfer = DictVectorizer(sparse=True)
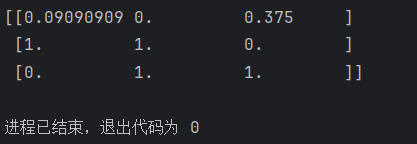
data_new = transfer.fit_transform(data)
print("data_new:\n", data_new)
x = data_new.toarray() # 转换为稠密矩阵
print(type(x))
print(x)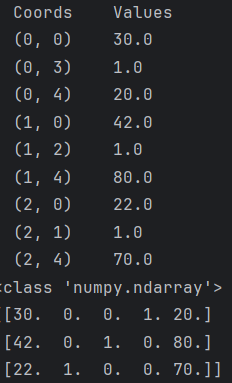
鸢尾花数据集划分
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
iris = load_iris()
list = train_test_split(iris.data, iris.target, test_size=0.2, random_state=22)
#x_train训练特征数据集,x_test测试特征数据集, y_train训练目标数据集,y_test测试目标数据集,
x_train, x_test, y_train, y_test = list
#打印结果为: (120, 4) (30, 4) (120,) (30,)
print(x_train.shape, x_test.shape, y_train.shape, y_test.shape)现实世界数据集划分
注:需联网执行对应操作
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
import numpy as np
news = fetch_20newsgroups(data_home=None, subset='all')
list = train_test_split(news.data, news.target,test_size=0.2, random_state=22)
# 返回值是一个list:其中有4个值,分别为训练集特征、测试集特征、训练集目标、测试集目标
# 与iris相同点在于x_train和x_test是列表,而iris是
x_train, x_test, y_train, y_test = list
#打印结果为: 15076 3770 (15076,) (3770,)
print(len(x_train), len(x_test), y_train.shape, y_test.shape)四、特征工程
特征工程:就是对特征进行相关的处理,就是将任意数据(如文本或图像)转换为可用于机器学习的数字特征,比如:字典特征提取(特征离散化)、文本特征提取、图像特征提取。
特征工程步骤为:
-
特征提取, 如果不是像dataframe那样的数据,要进行特征提取,比如字典特征提取,文本特征提取
-
无量纲化(预处理)
-
归一化
-
标准化
-
-
降维
-
底方差过滤特征选择
-
主成分分析-PCA降维
-
| DictVectorizer | 字典特征提取 |
| CountVectorizer | 文本特征提取 |
| TfidfVectorizer | TF-IDF文本特征词的重要程度特征提取 |
| MinMaxScaler | 归一化 |
| StandardScaler | 标准化 |
| VarianceThreshold | 底方差过滤降维 |
| PCA | 主成分分析降维 |
稀疏矩阵
稀疏矩阵是指一个矩阵中大部分元素为零,只有少数元素是非零的矩阵。在数学和计算机科学中,当一个矩阵的非零元素数量远小于总的元素数量,且非零元素分布没有明显的规律时,这样的矩阵就被认为是稀疏矩阵。例如,在一个1000 x 1000的矩阵中,如果只有1000个非零元素,那么这个矩阵就是稀疏的。
由于稀疏矩阵中零元素非常多,存储和处理稀疏矩阵时,通常会采用特殊的存储格式,以节省内存空间并提高计算效率。
非稀疏矩阵(稠密矩阵)
非稀疏矩阵,或称稠密矩阵,是指矩阵中非零元素的数量与总元素数量相比接近或相等,也就是说矩阵中的大部分元素都是非零的。在这种情况下,矩阵的存储通常采用标准的二维数组形式,因为非零元素密集分布,不需要特殊的压缩或优化存储策略。
-
存储:稀疏矩阵使用特定的存储格式来节省空间,而稠密矩阵使用常规的数组存储所有元素,无论其是否为零。
-
计算:稀疏矩阵在进行计算时可以利用零元素的特性跳过不必要的计算,从而提高效率。而稠密矩阵在计算时需要处理所有元素,包括零元素。
-
应用领域:稀疏矩阵常见于大规模数据分析、图形学、自然语言处理、机器学习等领域,而稠密矩阵在数学计算、线性代数等通用计算领域更为常见。
在实际应用中,选择使用稀疏矩阵还是稠密矩阵取决于具体的问题场景和数据特性。
DcitVectorizer字典列表特征提取
from sklearn.feature_extraction import DictVectorizer
data = [{'city':'成都', 'age':30, 'temperature':200}, {'city':'重庆','age':33, 'temperature':60}, {'city':'北京', 'age':42, 'temperature':80}]
#创建DictVectorizer对象
transfer = DictVectorizer(sparse=False)
data_new = transfer.fit_transform(data)
# data_new的类型为ndarray
#特征数据
print("data_new:\n", data_new)
#特征名字
print("特征名字:\n", transfer.get_feature_names_out())
CountVectorizer文本特征提取
from sklearn.feature_extraction.text import CountVectorizer
import pandas as pd
data=["stu is well, stu is great", "You like stu"]
#创建转换器对象, you和is不提取
transfer = CountVectorizer(stop_words=["you","is"])
#进行提取,得到稀疏矩阵
data_new = transfer.fit_transform(data)
print(data_new)df=pd.DataFrame(data_new.toarray(),index=["第一个句子","第二个句子"],columns=transfer.get_feature_names_out())
print(df)
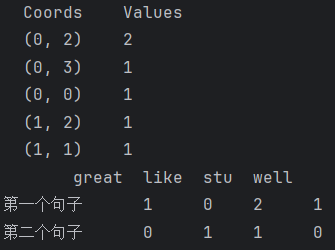
TfidfVectorizer TF-IDF文本特征提取词

词频 (TF)
词频是指一个词在文档中出现的频率。通常有两种计算方法:
-
原始词频:一个词在文档中出现的次数除以文档中总的词数。
-
平滑后的词频:为了防止高频词主导向量空间,有时会对词频进行平滑处理,例如使用
1 + log(TF)。 -
在 TfidfVectorizer 中,TF 默认是:直接使用一个词在文档中出现的次数也就是CountVectorizer的结果
逆文档频率 (IDF)
逆文档频率衡量一个词的普遍重要性。如果一个词在许多文档中都出现,那么它的重要性就会降低。

import jieba #中文分词库
import pandas as pd
from sklearn.feature_extraction.text import TfidfVectorizerdef cut_words(text):return " ".join(list(jieba.cut(text))) #将转为列表的分词结果用空格连接成字符串data = ["教育学会会长期间,坚定支持民办教育事业!", "扶持民办,学校发展事业","事业做出重大贡献!"]
data_new = [cut_words(v) for v in data]transfer = TfidfVectorizer(stop_words=['期间', '做出',"重大贡献"]) #将文本转换为TF-IDF特征矩阵
data_final = transfer.fit_transform(data_new) #同时完成词汇学习和特征转换
# 将稀疏矩阵转换为稠密数组 #获取所有特征词
pd.DataFrame(data_final.toarray(), columns=transfer.get_feature_names_out())

五、无量纲化-预处理
无量即无单位的数据
MinMaxScaler归一化

这里的 𝑥min 和 𝑥max 分别是每种特征中的最小值和最大值,而 𝑥是当前特征值,𝑥scaled 是归一化后的特征值。
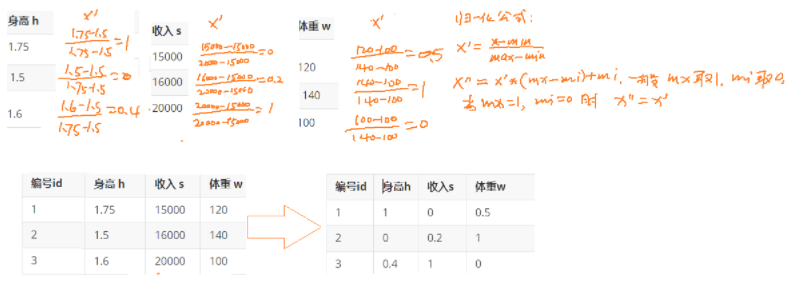
原始数据类型为list
from sklearn.preprocessing import MinMaxScaler
data=[[12,22,4],[22,23,1],[11,23,9]]
#feature_range=(0, 1)表示归一化后的值域,可以自己设定
transfer = MinMaxScaler(feature_range=(0, 1))
#data_new的类型为<class 'numpy.ndarray'>
data_new = transfer.fit_transform(data)
print(data_new)缺点
最大值和最小值容易受到异常点影响,所以鲁棒性较差。所以常使用标准化的无量钢化
normalize归一化
归一化的核心是将不同特征的取值范围统一,使得模型在训练时不会被量级较大的特征主导。
from sklearn.datasets import load_iris
from sklearn.preprocessing import normalize
x,y=load_iris(return_X_y=True)
x=normalize(x,norm="max",axis=0) # l1 l2 max
print(x[:10])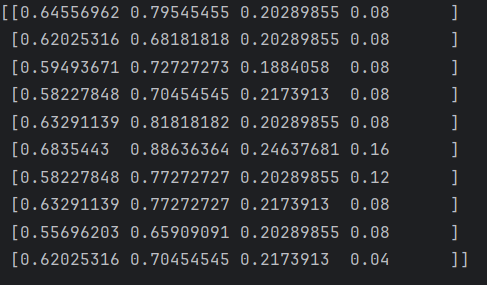
<1> L1归一化
绝对值相加作为分母,特征值作为分子
<2> L2归一化
平方相加作为分母,特征值作为分子
<3> max归一化
max作为分母,特征值作为分子
StandardScaler标准化
最常见的标准化方法是Z-score标准化,也称为零均值标准化。它通过对每个特征的值减去其均值,再除以其标准差,将数据转换为均值为0,标准差为1的分布。这可以通过以下公式计算:
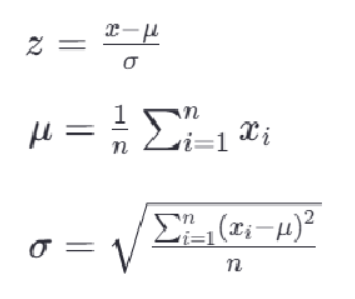
其中,z是转换后的数值,x是原始数据的值,μ是该特征的均值,σ是该特征的 标准差
import pandas as pd
from sklearn.preprocessing import StandardScaler
# 1、获取数据
df_data = pd.read_csv("./dating.txt")
print(type(df_data)) #<class 'pandas.core.frame.DataFrame'>
print(df_data.shape) #(1000, 4)# 2、实例化一个转换器类
transfer = StandardScaler()# 3、调用fit_transform
new_data = transfer.fit_transform(df_data) #把DateFrame数据进行归一化
print("DateFrame数据被归一化后:\n", new_data[0:5])nd_data = df_data.values #把DateFrame转为ndarray
new_data = transfer.fit_transform(nd_data) #把ndarray数据进行归一化
print("ndarray数据被归一化后:\n", new_data[0:5])nd_data = df_data.values.tolist() #把DateFrame转为list
new_data = transfer.fit_transform(nd_data) #把ndarray数据进行归一化
print("list数据被归一化后:\n", new_data[0:5])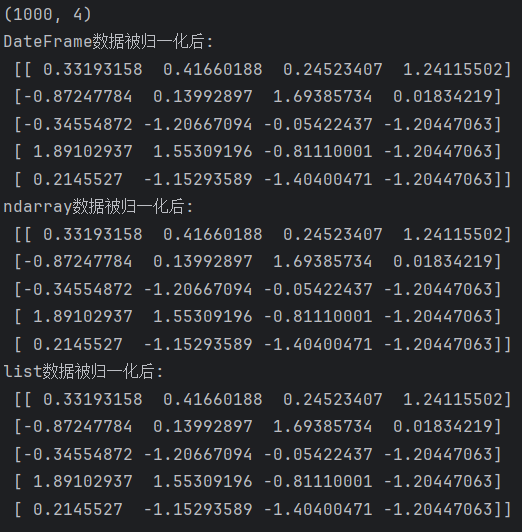
在数据预处理中,特别是使用如StandardScaler这样的数据转换器时,fit、fit_transform和transform这三个方法的使用是至关重要的,它们各自有不同的作用:
-
fit:
-
这个方法用来计算数据的统计信息,比如均值和标准差(在
StandardScaler的情况下)。这些统计信息随后会被用于数据的标准化。 -
你应当仅在训练集上使用
fit方法。
-
-
fit_transform:
-
这个方法相当于先调用
fit再调用transform,但是它在内部执行得更高效。 -
它同样应当仅在训练集上使用,它会计算训练集的统计信息并立即应用到该训练集上。
-
-
transform:
-
这个方法使用已经通过
fit方法计算出的统计信息来转换数据。 -
它可以应用于任何数据集,包括训练集、验证集或测试集,但是应用时使用的统计信息必须来自于训练集。
-
当你在预处理数据时,首先需要在训练集X_train上使用fit_transform,这样做可以一次性完成统计信息的计算和数据的标准化。这是因为我们需要确保模型是基于训练数据的统计信息进行学习的,而不是整个数据集的统计信息。
一旦scaler对象在X_train上被fit,它就已经知道了如何将数据标准化。这时,对于测试集X_test,我们只需要使用transform方法,因为我们不希望在测试集上重新计算任何统计信息,也不希望测试集的信息影响到训练过程。如果我们对X_test也使用fit_transform,测试集的信息就可能会影响到训练过程。
总结来说:我们常常是先fit_transform(x_train)然后再transform(x_text)
六、特征降维
降维就是去掉一些特征,或者转化多个特征为少量个特征
特征降维其目的:是减少数据集的维度,同时尽可能保留数据的重要信息。
特征降维的好处:
减少计算成本:在高维空间中处理数据可能非常耗时且计算密集。降维可以简化模型,降低训练时间和资源需求。
去除噪声:高维数据可能包含许多无关或冗余特征,这些特征可能引入噪声并导致过拟合。降维可以帮助去除这些不必要的特征。
特征降维的方式:
特征选择
VarianceThreshold 低方差过滤特征选择
-
Filter(过滤式): 主要探究特征本身特点, 特征与特征、特征与目标值之间关联
-
方差选择法: 低方差特征过滤
如果一个特征的方差很小,说明这个特征的值在样本中几乎相同或变化不大,包含的信息量很少,模型很难通过该特征区分不同的对象,比如区分甜瓜子和咸瓜子还是蒜香瓜子,如果有一个特征是长度,这个特征相差不大可以去掉。
-
计算方差:对于每个特征,计算其在训练集中的方差(每个样本值与均值之差的平方,在求平均)。
-
设定阈值:选择一个方差阈值,任何低于这个阈值的特征都将被视为低方差特征。
-
过滤特征:移除所有方差低于设定阈值的特征
-
-
from sklearn.feature_selection import VarianceThreshold
import pandas as pd
def variance_demo():# 1、获取数据,data是一个DataFrame,可以是读取的csv文件data=pd.DataFrame([[10,1],[11,3],[11,1],[11,5],[11,9],[11,3],[11,2],[11,6]])print("data:\n", data)# 2、实例化一个转换器类transfer = VarianceThreshold(threshold=1)# 1阈值# 3、调用fit_transform 先计算每个特征的方差,再根据阈值筛选特征data_new = transfer.fit_transform(data)print("data_new:\n",data_new)return None
variance_demo()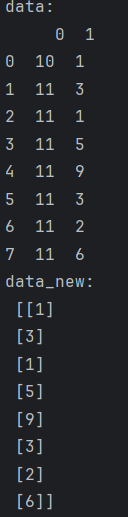
相关系数特征选择
正相关性(Positive Correlation)是指两个变量之间的一种统计关系,其中一个变量的增加通常伴随着另一个变量的增加,反之亦然。在正相关的关系中,两个变量的变化趋势是同向的。当我们说两个变量正相关时,意味着:
-
如果第一个变量增加,第二个变量也有很大的概率会增加。
-
同样,如果第一个变量减少,第二个变量也很可能会减少。
正相关性并不意味着一个变量的变化直接引起了另一个变量的变化,它仅仅指出了两个变量之间存在的一种统计上的关联性。这种关联性可以是因果关系,也可以是由第三个未观察到的变量引起的,或者是纯属巧合。
在数学上,正相关性通常用正值的相关系数来表示,这个值介于0和1之间。当相关系数等于1时,表示两个变量之间存在完美的正相关关系,即一个变量的值可以完全由另一个变量的值预测。
举个例子,假设我们观察到在一定范围内,一个人的身高与其体重呈正相关,这意味着在一般情况下,身高较高的人体重也会较重。但这并不意味着身高直接导致体重增加,而是可能由于营养、遗传、生活方式等因素共同作用的结果。
负相关性(Negative Correlation)与正相关性刚好相反,但是也说明相关,比如运动频率和BMI体重指数程负相关
不相关指两者的相关性很小,一个变量变化不会引起另外的变量变化,只是没有线性关系. 比如饭量和智商
皮尔逊相关系数(Pearson correlation coefficient)是一种度量两个变量之间线性相关性的统计量。它提供了两个变量间关系的方向(正相关或负相关)和强度的信息。皮尔逊相关系数的取值范围是 [−1,1],其中:
-
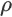 =1 表示完全正相关,即随着一个变量的增加,另一个变量也线性增加。
=1 表示完全正相关,即随着一个变量的增加,另一个变量也线性增加。 -
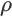 =-1 表示完全负相关,即随着一个变量的增加,另一个变量线性减少。
=-1 表示完全负相关,即随着一个变量的增加,另一个变量线性减少。 -
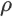 =0 表示两个变量之间不存在线性关系。
=0 表示两个变量之间不存在线性关系。
相关系数\rho的绝对值为0-1之间,绝对值越大,表示越相关,当两特征完全相关时,两特征的值表示的向量是
在同一条直线上,当两特征的相关系数绝对值很小时,两特征值表示的向量接近在同一条直线上。当相关系值为负数时,表示负相关
皮尔逊相关系数:pearsonr相关系数计算公式, 该公式出自于概率论
对于两组数据 𝑋={𝑥1,𝑥2,...,𝑥𝑛} 和 𝑌={𝑦1,𝑦2,...,𝑦𝑛},皮尔逊相关系数可以用以下公式计算:
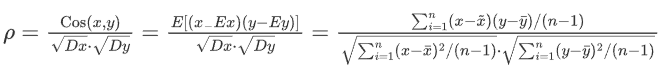
分别是𝑋和𝑌的平均值
|ρ|<0.4为低度相关; 0.4<=|ρ|<0.7为显著相关; 0.7<=|ρ|<1为高度相关
from scipy.stats import pearsonr
import pandas as pd
def association_demo():# 获取数据data = pd.read_csv("./factor_returns.csv")data = data.iloc[:, 1:-2]# 计算某两个变量之间的相关系数r1 = pearsonr(data["pe_ratio"], data["pb_ratio"])print(r1.statistic) #-0.0043893227799362555 相关性, 负数表示负相关,正数表示正相关print(r1.pvalue) #0.8327205496590723 相关性,越小越相关# 选取所有行,列从索引1到倒数第3列r2 = pearsonr(data['revenue'], data['total_expense'])print(r2) #PearsonRResult(statistic=0.9958450413136111, pvalue=0.0)return None
association_demo()
主成分分析
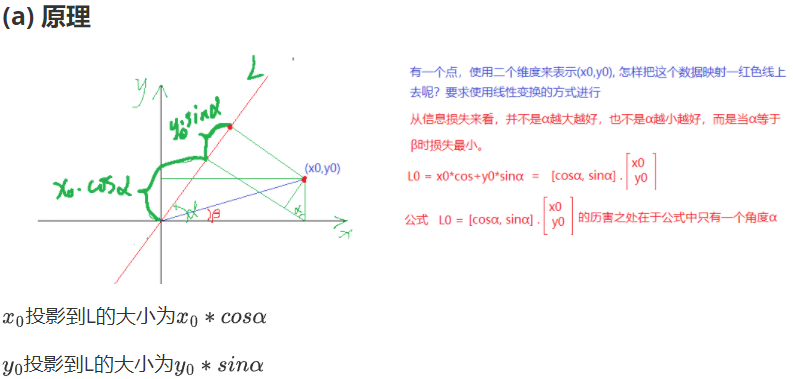
使用(x_0,y_0)表示一个点, 表明该点有两个特征, 而映射到L上有一个特征就可以表示这个点了。这就达到了降维的功能 。
投影到L上的值就是降维后保留的信息,投影到与L垂直的轴上的值就是丢失的信息。保留信息/原始信息=信息保留的比例
下图中红线上点与点的距离是最大的,所以在红色线上点的方差最大,粉红线上的刚好相反.
所以红色线上点来表示之前点的信息损失是最小的。
比如下图的二维数据要降为一维数据,图形法是把所在数据在二维坐标中以点的形式标出,然后给出一条直线,让所有点垂直映射到直线上,该直线有很多,只有点到线的距离之和最小的线才能让之前信息损失最小。
这样之前所有的二维表示的点就全部变成一条直线上的点,从二维降成了一维。
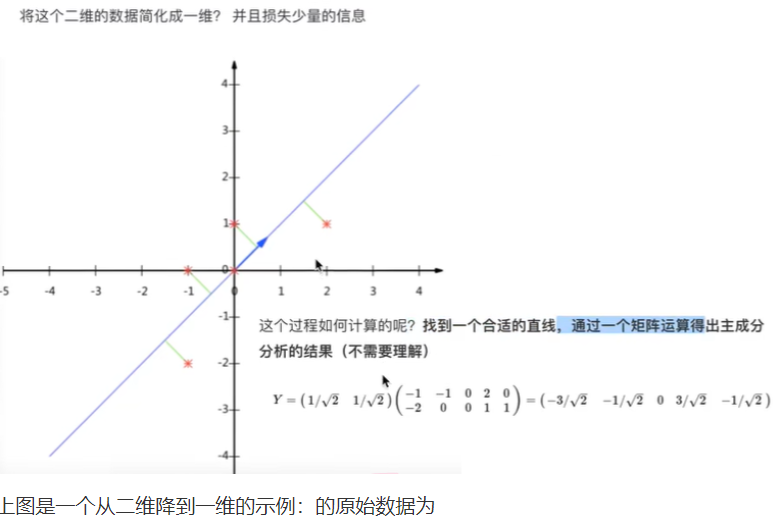
| 特征1-X1 | 特征2-X2 |
|---|---|
| -1 | -2 |
| -1 | 0 |
| 0 | 0 |
| 2 | 1 |
| 0 | 1 |
降维后的新数据为:
| 特征3-X0 |
|---|
| -3/√2 |
| -1/√2 |
| 0 |
| 3/√2 |
| -1/√2 |
from sklearn.decomposition import PCA
def pca_demo():data = [[2,8,4,5], [6,3,0,8], [5,4,9,1]]# 1.实例化一个转换器类,降维后还要保留原始数据0.95%的信息, 最后的结果中发现由4个特征降维成2个特征了transfer = PCA(n_components=0.95) #小数为保留比例,整数为减少到多少特征# 2.调用fit_transform 先分析数据特征,再将数据映射到新空间data_new = transfer.fit_transform(data)print("data_new:\n", data_new)return None
pca_demo()
七、KNN算法
样本距离判断
| 明可夫斯基距离 |
| 欧式距离,明可夫斯基距离的特殊情况 |
| 曼哈顿距离,明可夫斯基距离的特殊情况 |
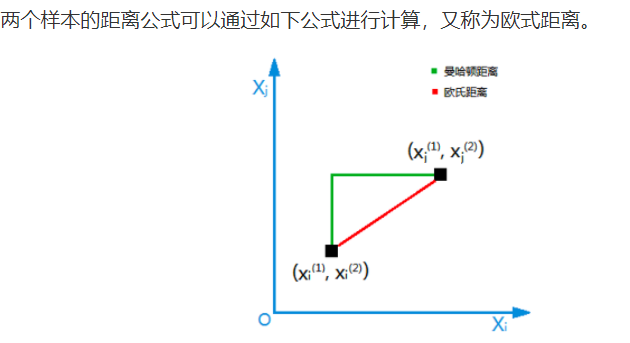
(1)欧氏距离
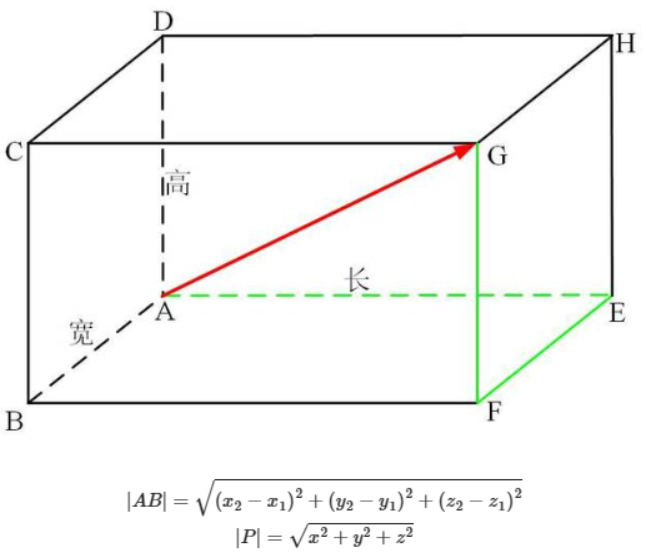
(2)曼哈顿距离
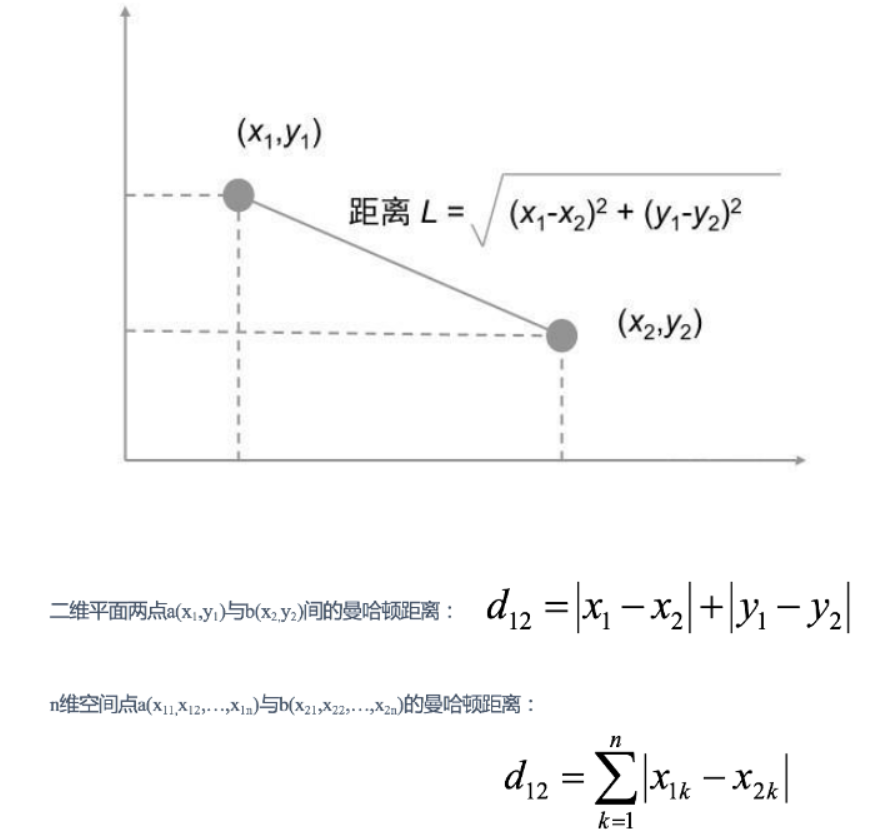
KNN算法
原理
K-近邻算法(K-Nearest Neighbors,简称KNN),根据K个邻居样本的类别来判断当前样本的类别;
如果一个样本在特征空间中的k个最相似(最邻近)样本中的大多数属于某个类别,则该类本也属于这个类别
比如: 有10000个样本,选出7个到样本A的距离最近的,然后这7个样本中假设:类别1有2个,类别2有3个,类别3有2个.那么就认为A样本属于类别2,因为它的7个邻居中 类别2最多(近朱者赤 近墨者黑)
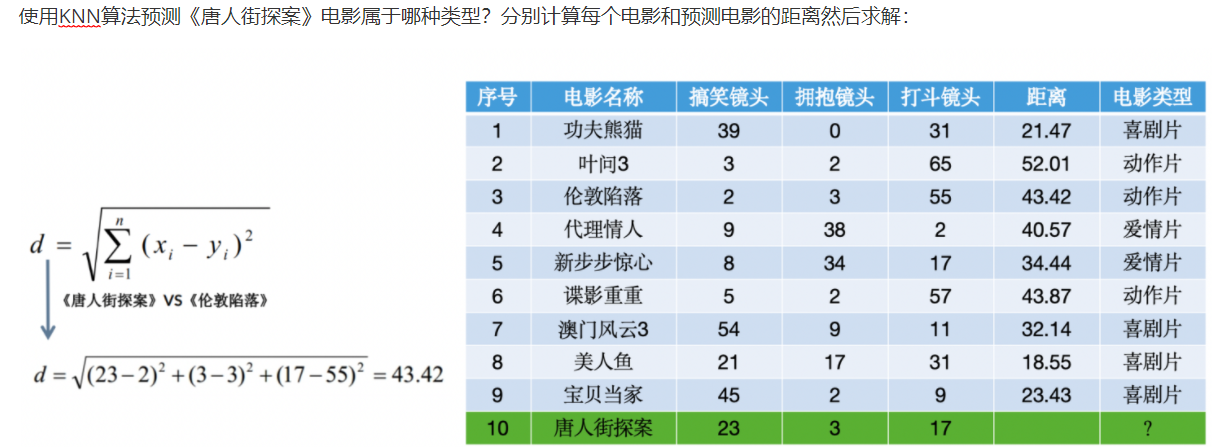
将要判断的类与距离自己最近的类型比较,一般取最近的几个(自主设置)数据类型作为新数据的类型
缺点
对于大规模数据集,计算量大,因为需要计算测试样本与所有训练样本的距离。
对于高维数据,距离度量可能变得不那么有意义,这就是所谓的“维度灾难”
需要选择合适的k值和距离度量,这可能需要一些实验和调整
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
import numpy as np# 加载数据集
iris=load_iris()
x=iris.data
y=iris.target
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=22)# 工程化
transfer=StandardScaler()
x_train=transfer.fit_transform(x_train)
x_test=transfer.transform(x_test)
# 训练
model=KNeighborsClassifier(n_neighbors=10) #初始化KNN模型,近邻数设为10
model.fit(x_train,y_train)
# 评估
y_predict=model.predict(x_test) #对测试集样本进行分类预测
print(y_predict)
print(x_test[:10])
print(y_predict==y_test)
score=np.sum(y_predict==y_test)/len(y_test) #计算准确率True相加次数除总次数
print(score)
print(model.score(x_test,y_test)) #模型的准确率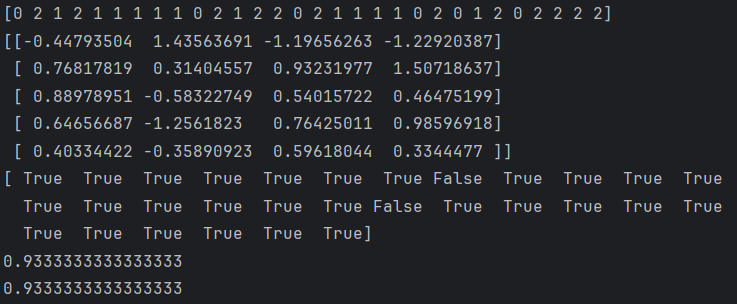
模型保存与加载
import joblib
# 保存模型
joblib.dump(estimator, "my_ridge.pkl")
# 加载模型
estimator = joblib.load("my_ridge.pkl")
#使用模型预测
y_test=estimator.predict([[0.4,0.2,0.4,0.7]])
print(y_test)八、模型选择和调优
交叉验证
保留交叉验证HoldOut
在这种交叉验证技术中,整个数据集被随机地划分为训练集和验证集。根据经验法则,整个数据集的近70%被用作训练集,其余30%被用作验证集。也就是我们最常使用的,直接划分数据集的方法。
优点:很简单很容易执行。
缺点1:不适用于不平衡的数据集。假设我们有一个不平衡的数据集,有0类和1类。假设80%的数据属于 “0 “类,其余20%的数据属于 “1 “类。这种情况下,训练集的大小为80%,测试数据的大小为数据集的20%。可能发生的情况是,所有80%的 “0 “类数据都在训练集中,而所有 “1 “类数据都在测试集中。因此,我们的模型将不能很好地概括我们的测试数据,因为它之前没有见过 “1 “类的数据。
缺点2:一大块数据被剥夺了训练模型的机会。
在小数据集的情况下,有一部分数据将被保留下来用于测试模型,这些数据可能具有重要的特征,而我们的模型可能会因为没有在这些数据上进行训练而错过。
K-折交叉验证(K-fold)
(K-fold Cross Validation,记为K-CV或K-fold)
K-Fold交叉验证技术中,整个数据集被划分为K个大小相同的部分。每个分区被称为 一个”Fold”。所以我们有K个部分,我们称之为K-Fold。一个Fold被用作验证集,其余的K-1个Fold被用作训练集。
该技术重复K次,直到每个Fold都被用作验证集,其余的作为训练集。
模型的最终准确度是通过取k个模型验证数据的平均准确度来计算的。
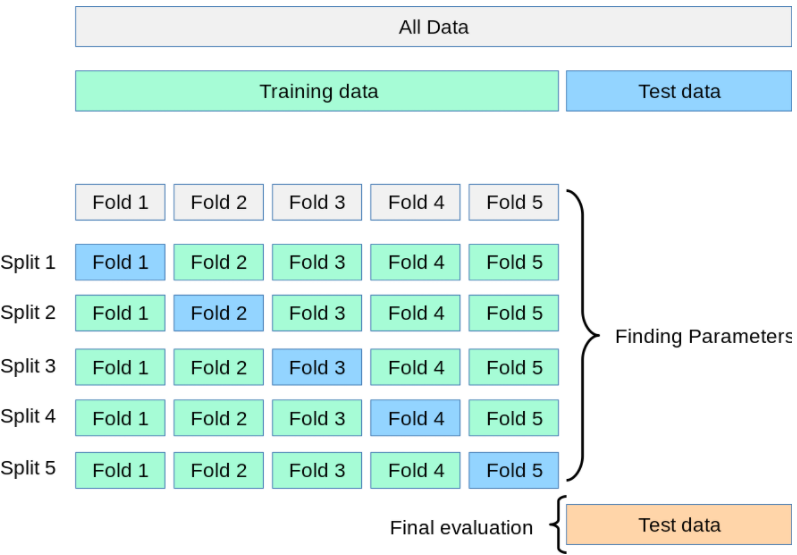
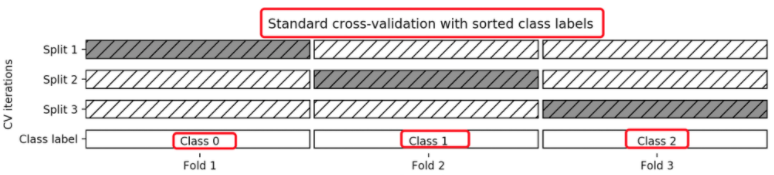
分层l-折交叉验证(Stratified k-fold)
Stratified k-fold cross validation,
K-折交叉验证的变种, 分层的意思是说在每一折中都保持着原始数据中各个类别的比例关系,比如说:原始数据有3类,比例为1:2:1,采用3折分层交叉验证,那么划分的3折中,每一折中的数据类别保持着1:2:1的比例,这样的验证结果更加可信。
其他验证
去除p交叉验证
去留 p 交叉验证是 LOOCV 的扩展,每次保留 p 个样本 作为测试集(p≥2),其余作为训练集,重复所有可能的组合后取平均性能。
2.适用场景与优缺点
适用场景:极小样本数据集(n≤20,p 通常取 2~5),需平衡测试集信息量与计算量。
优点:比 LOOCV 的测试集更大(更接近真实场景),结果更可靠。
缺点:计算量随 p 增大急剧增加(如 n=20, p=5 时,组合数 = 15504,训练 15504 次),实际中极少使用。
留一交叉验证
留一交叉验证是去留 p 交叉验证的特殊情况(p=1),核心是每次只保留 1 个样本作为测试集,其余全部作为训练集,重复所有样本后取平均性能。

2.适用场景与优缺点
适用场景:小样本数据集(n≤50),需充分利用数据(每个样本都作为测试集)。
优点:无随机划分偏差,结果稳定;充分利用数据,适合数据稀缺场景。
缺点:计算成本极高(需训练 n 次模型),n 较大时(如 n=1000)几乎不可用。
蒙特卡罗交叉验证
蒙特卡洛交叉验证(又称随机交叉验证)通过随机重复划分训练集和测试集(不要求覆盖所有样本),用多次结果的平均值评估模型,核心是 “随机性 + 多次重复”。
2.适用场景与优缺点
适用场景:大样本数据集(n≥1000),需平衡计算成本与结果稳定性。
优点:计算量可控(k 可灵活调整);随机性降低划分偏差,结果稳健。
缺点:可能存在样本未被选为测试集(信息利用不充分);k 较小时结果波动大。
时间序列交叉验证
时间序列数据具有时序依赖性(如股票价格、天气数据),不能随机划分(否则导致 “未来数据泄露到过去”),需按时间顺序划分训练集和测试集。

2.其他变种
扩展窗口验证:训练集随时间累积(不固定窗口大小),如
T 1={t1−t3},T2={t1−t4},...,适合数据量随时间增长的场景。滑动多步验证:测试集包含多个未来样本(如 V1={t4−t5}),适合预测短期趋势。
3.适用场景与优缺点
适用场景:时间序列数据(如金融、气象、销售预测),需避免 “未来信息泄露”。
优点:符合时间序列的时序特性,评估结果更贴近真实预测场景。
缺点:训练集随时间滚动,计算成本随 n 增大而增加;早期样本可能因数据分布变化失效(需结合窗口更新策略)。
| 方法 | 核心逻辑 | 数据划分特点 | 适用场景 | 计算成本 | 结果稳定性 |
|---|---|---|---|---|---|
| 留一交叉验证 | 每次留 1 个样本测试,重复 n 次 | 覆盖所有样本作为测试集 | 小样本(n≤50) | 极高 | 高 |
| 去留 p 交叉验证 | 每次留 p 个样本测试,重复 C (n,p) 次每次留 p 个样本测试,重复 C (n,p) 次 | 测试集含 p 个样本 | 极小样本(n≤20) | 极高 | 高 |
| 蒙特卡洛交叉验证 | 随机划分训练 / 测试集,重复 k 次 | 允许样本重叠,不强制覆盖 | 大样本(n≥1000) | 中 | 中(随k增) |
| 时间序列交叉验证 | 按时间顺序滚动划分,避免数据泄露 | 训练集始终在测试集之前 | 时序数据(如预测) | 中 | 中 |
超参数搜索

from sklearn.model_selection import GridSearchCV #网格搜索工具GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
x,y=load_iris(return_X_y=True)knn=KNeighborsClassifier(n_neighbors=7) #初始化KNN分类器,最近邻选择7个
# param_grid:定义要搜索的参数及候选值
model=GridSearchCV(knn,param_grid={"n_neighbors":
[1,2,3,4,5,6,7,8,9,10]},cv=5) #使用 5 折交叉验证评估每个参数的性能
model.fit(x,y)print(model.best_params_) # 最佳超参数组合
print(model.best_score_) # 最佳模型的交叉验证平均得分
print(model.best_index_) # 最佳参数在param_grid中的索引
print(model.best_estimator_) # 最佳参数对应的模型对象#使用模型
y_pre=model.predict(x) #使用最优参数训练的模型对x预测
print(y_pre)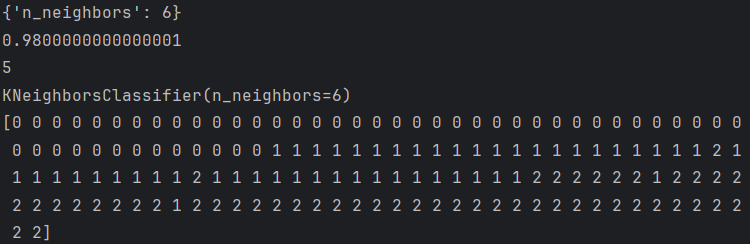
九、朴素贝叶斯分类
贝叶斯思想
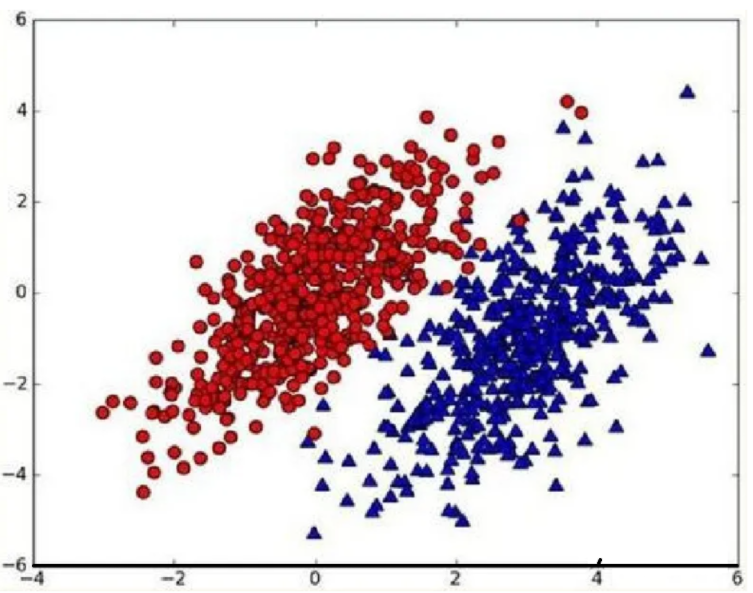
假设有一个数据集,将其分为两个类别
我们现在用p1(x,y)表示数据点(x,y)属于类别1(图中红色圆点表示的类别)的概率,用p2(x,y)表示数据点(x,y)属于类别2(图中蓝色三角形表示的类别)的概率,那么对于一个新数据点(x,y),可以用下面的规则来判断它的类别:
-
如果p1(x,y)>p2(x,y),那么类别为1
-
如果p1(x,y)<p2(x,y),那么类别为2
也就是说,我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。已经了解了贝叶斯决策理论的核心思想,那么接下来,就是学习如何计算p1和p2概率。
贝叶斯推断
条件概率公式
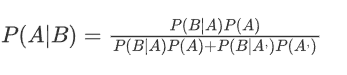
对条件概率公式进行变形,可以得到如下形式
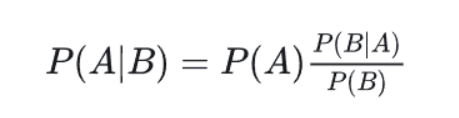
我们把P(A)称为"先验概率"(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。
P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。
P(B|A)/P(B)称为"可能性函数"(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
所以,条件概率可以理解成下面的式子:
后验概率 = 先验概率x调整因子
这就是贝叶斯推断的含义。我们先预估一个"先验概率",然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率",由此得到更接近事实的"后验概率"。
朴素贝叶斯推断
理解了贝叶斯推断,那么让我们继续看看朴素贝叶斯。贝叶斯和朴素贝叶斯的概念是不同的,区别就在于“朴素”二字,朴素贝叶斯对条件概率分布做了条件独立性的假设。 比如下面的公式,假设有n个特征:
根据贝叶斯定理,后验概率 P(a|X) 可以表示为:
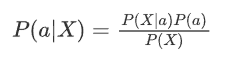
其中:
-
P(X|a) 是给定类别 ( a ) 下观测到特征向量 X=(x1, x2, ..., xn) 的概率;
-
P(a) 是类别 a 的先验概率;
-
P(X) 是观测到特征向量 X 的边缘概率,通常作为归一化常数处理。
朴素贝叶斯分类器的关键假设是特征之间的条件独立性,即给定类别 a ,特征 xi 和 xj (其中 i \neq j 相互独立。)
因此,我们可以将联合概率 P(X|a) 分解为各个特征的概率乘积:

这样,朴素贝叶斯分类器就可以通过计算每种可能类别的条件概率和先验概率,然后选择具有最高概率的类别作为预测结果。
拉普拉斯平滑系数
某些事件或特征可能从未出现过,这会导致它们的概率被估计为零。然而,在实际应用中,即使某个事件或特征没有出现在训练集中,也不能完全排除它在未来样本中出现的可能性。拉普拉斯平滑技术可以避免这种“零概率陷阱”
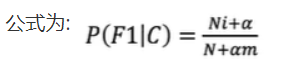
一般α取值1,m的值为总特征数量
通过这种方法,即使某个特征在训练集中从未出现过,它的概率也不会被估计为零,而是会被赋予一个很小但非零的值,从而避免了模型在面对新数据时可能出现的过拟合或预测错误
十、决策树分类
1、决策节点 通过条件判断而进行分支选择的节点。如:将某个样本中的属性值(特征值)与决策节点上的值进行比较,从而判断它的流向。
2、叶子节点没有子节点的节点,表示最终的决策结果。
3、决策树的深度所有节点的最大层次数。
决策树具有一定的层次结构,根节点的层次数定为0,从下面开始每一层子节点层次数增加
4、决策树优点:
可视化 - 可解释能力-对算力要求低
5、 决策树缺点:
容易产生过拟合,所以不要把深度调整太大了。
基于信息增益决策树的建立
信息增益决策树倾向于选择取值较多的属性,在有些情况下这类属性可能不会提供太多有价值的信息,算法只能对描述属性为离散型属性的数据集构造决策树。
根据以下信息构建一棵预测是否贷款的决策树。我们可以看到有4个影响因素:职业,年龄,收入和学历。
| 职业 | 年龄 | 收入 | 学历 | 是否贷款 | |
|---|---|---|---|---|---|
| 1 | 工人 | 36 | 5500 | 高中 | 否 |
| 2 | 工人 | 42 | 2800 | 初中 | 是 |
| 3 | 白领 | 45 | 3300 | 小学 | 是 |
| 4 | 白领 | 25 | 10000 | 本科 | 是 |
| 5 | 白领 | 32 | 8000 | 硕士 | 否 |
| 6 | 白领 | 28 | 13000 | 博士 | 是 |
信息熵
信息熵描述的是不确定性。信息熵越大,不确定性越大。信息熵的值越小,则D的纯度越高。
假设样本集合D共有N类,第k类样本所占比例为Pk,则D的信息熵为
![]()
信息增益
信息增益是一个统计量,用来描述一个属性区分数据样本的能力。信息增益越大,那么决策树就会越简洁。这里信息增益的程度用信息熵的变化程度来衡量, 信息增益公式:
![]()
信息增益决策树建立步骤


基于基尼指数决策树建立
基尼指数(Gini Index)是决策树算法中用于评估数据集纯度的一种度量,基尼指数衡量的是数据集的不纯度,或者说分类的不确定性。在构建决策树时,基尼指数被用来决定如何对数据集进行最优划分,以减少不纯度。

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier,export_graphviz
from sklearn.model_selection import train_test_splitx,y=load_iris(return_X_y=True)
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=0)
model=DecisionTreeClassifier(max_depth=5,criterion='entropy') #entropy信息增益法 也可以选择gini法
model.fit(x_train,y_train)
print(model.score(x_test,y_test))y_predict=model.predict([[4.2,2.1,3.4,2.1]]) #使用二维数组
print(y_predict)预测100%因为模型数据已训练过很多次并且模型数据简单,高度可分.
并且此处预测为第三种鸢尾花 ( [0] [1] [2] )

十一、集成学习之随机森林
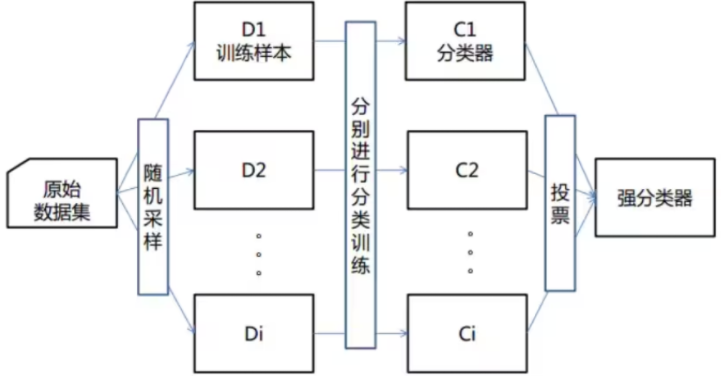
-
随机: 特征随机,训练集随机
-
样本:对于一个总体训练集T,T中共有N个样本,每次有放回地随机选择n个样本。用这n个样本来训练一个决策树。
-
特征:假设训练集的特征个数为d,每次仅选择k(k<d)个来构建决策树。
-
-
森林: 多个决策树分类器构成的分类器, 因为随机,所以可以生成多个决策树
-
处理具有高维特征的输入样本,而且不需要降维
-
使用平均或者投票来提高预测精度和控制过拟合
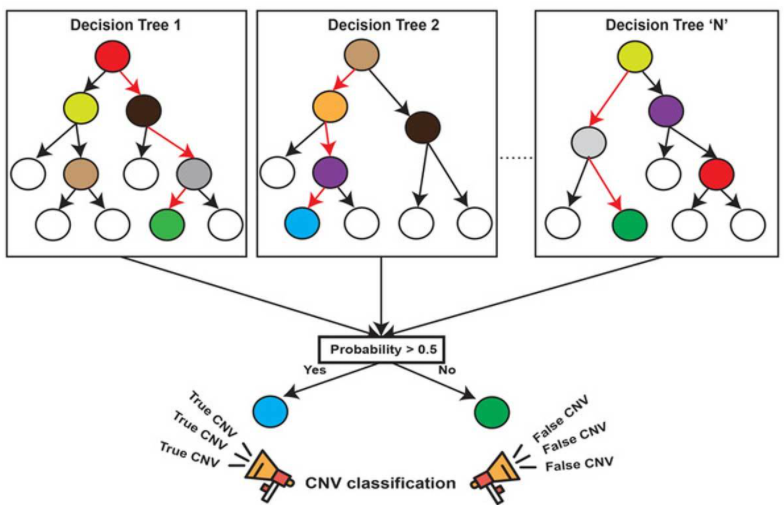
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import RandomForestClassifier
# 提取特征 x 和标签 y
x,y=load_iris(return_X_y=True)
# 划分数据集:测试集占20%,固定随机种子确保结果可复现
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=0)
# 初始化标准化器
scaler=StandardScaler()
# 拟合训练集并标准化
x_train=scaler.fit_transform(x_train)
# 用训练集的标准化规则处理测试集
x_test=scaler.transform(x_test)
# 初始化随机森林:迭代100次,最大深度6,用信息熵作为分裂准则
model=RandomForestClassifier(n_estimators=100,max_depth=6,criterion="entropy")
model.fit(x_train,y_train)
# 计算测试集上的准确率
score=model.score(x_test,y_test)
print(score)y=model.predict([[1.1,2.2,4.0,3.8]])
print(y)
训练评估分约等于96.7%,并将输入的数据预测为第三种鸢尾花
十二、线性回归
回归的目的是预测数值型的目标值y。最直接的办法是依据输入x写出一个目标值y的计算公式。假如你想预测小姐姐男友汽车的功率,可能会这么计算:
HorsePower = 0.0015 * annualSalary - 0.99 * hoursListeningToPublicRadio
写成中文就是:
小姐姐男友汽车的功率 = 0.0015 * 小姐姐男友年薪 - 0.99 * 收听公共广播的时间
这就是所谓的回归方程(regression equation),其中的0.0015和-0.99称为回归系数(regression weights),求这些回归系数的过程就是回归。一旦有了这些回归系数,再给定输入,做预测就非常容易了。具体的做法是用回归系数乘以输入值,再将结果全部加在一起,就得到了预测值。
线性回归
一般都是指线性回归(linear regression)。线性回归意味着可以将输入项分别乘以一些常量,再将结果加起来得到输出。线性回归是机器学习中一种有监督学习的算法,回归问题主要关注的是因变量(需要预测的值)和一个或多个数值型的自变量(预测变量)之间的关系.
需要预测的值:即目标变量,target,y
影响目标变量的因素:X1,X2...Xn,可以是连续值也可以是离散值
因变量和自变量之间的关系:即模型,model,就是我们要求解的
比如1个包子是2元 3个包子是6元 预测5个包子多少钱
列出方程: y=wx+b
带入:
2=w*1+b
6=w*3+b
轻易求得 w=2 b=0
模型(x与y的关系): y=2*x+0
预测 x=5 时 target_y=2*5+0=10元
上面的方程式我们人类很多年以前就知道了,但是不叫人工智能算法,因为数学公式是理想状态,是100%对的,而人工智能是一种基于实际数据求解最优最接近实际的方程式,这个方程式带入实际数据计算后的结果是有误差的.
人工智能中的线性回归:数据集中,往往找不到一个完美的方程式来100%满足所有的y目标
我们就需要找出一个最接近真理的方程式
例如:
有这样一种植物,在不同的温度下生长的高度是不同的,对不同温度环境下,几颗植物的环境温度(横坐标),植物生长高度(纵坐标)的关系进行了采集,并且将它们绘制在一个二维坐标中,其分布如下图所示:
坐标分别为[4.2, 3.8],[4.2, 2.7],[2.7, 2.4],[0.8, 1.0],[3.7, 2.8],[1.7, 0.9],[3.2, 2.9]。
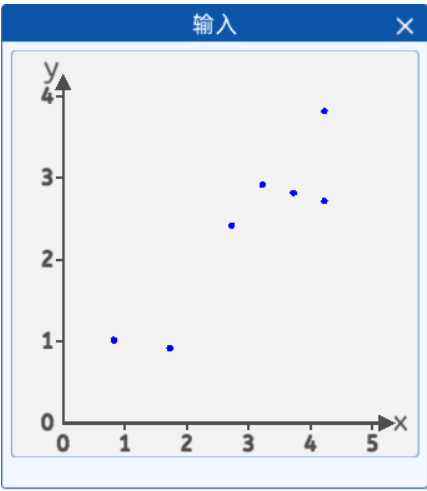
我们发现这些点好像分布在一条直线的附近,那么我们能不能找到这样一条直线,去“拟合”这些点,这样的话我们就可以通过获取环境的温度大概判断植物在某个温度下的生长高度了。
于是我们的最终目的就是通过这些散点来拟合一条直线,使该直线能尽可能准确的描述环境温度与植物高度的关系。
损失函数
数据: [[4.2, 3.8],[4.2, 2.7],[2.7, 2.4],[0.8, 1.0],[3.7, 2.8],[1.7, 0.9],[3.2, 2.9]]
我们假设 这个最优的方程是: y=wx+b
这样的直线随着w和b的取值不同 可以画出无数条
在这无数条中,哪一条是比较好的呢?
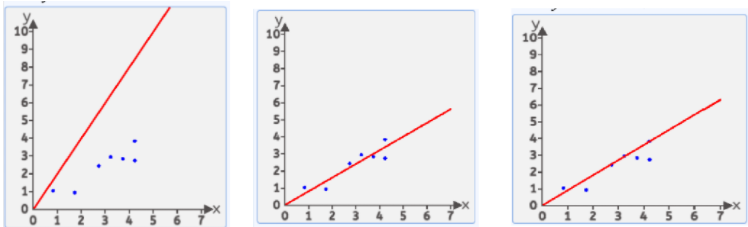
我们有很多方式认为某条直线是最优的,其中一种方式:均方差
就是每个点到线的竖直方向的距离平方 求和 在平均 最小时 这条直接就是最优直线
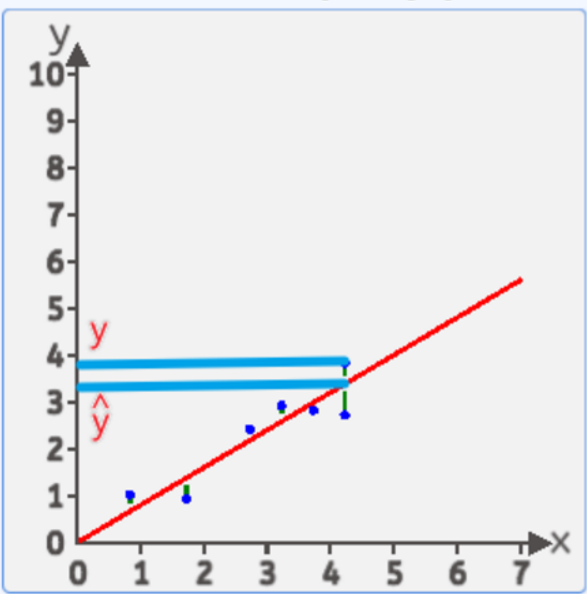
假设 y = wx+b , 把x1,x2,x3...带进去,便得到
![]()
![]()
![]() .......
.......
然后计算![]() 表示第一个点的真实值和计算值的差值 ,然后把第二个点,第三个点...最后一个点的差值全部算出来
表示第一个点的真实值和计算值的差值 ,然后把第二个点,第三个点...最后一个点的差值全部算出来
有的点在上面有点在下面,如果直接相加有负数和正数会抵消,体现不出来总误差,平方后就不会有这个问题了
所以最后:
总误差(也就是传说中的损失):
![]()
平均误差(总误差会受到样本点的个数的影响,样本点越多,该值就越大,所以我们可以对其平均化,求得平均值,这样就能解决样本点个数不同带来的影响)
这样就得到了传说中的损失函数:
![]()
如何让损失函数达到最小呢?先假设b=0(等后面多元方程求解这个b就解决了 )
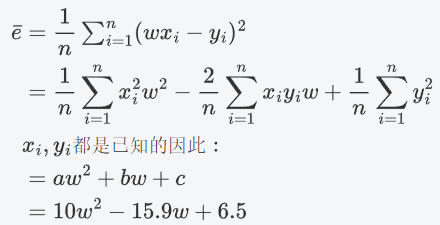
然后就简单了 算w在什么情况下损失函数的值最小(初中的抛物线求顶点的横坐标,高中求导数为0时)
求得w=0.795时损失函数取得最小值
那我们最终那个真理函数(最优解)就得到了
y = 0.795x + 0
总结:
1.实际数据中 x和y组成的点 不一定是全部落在一条直线上
2.我们假设有这么一条直线 y=wx+b 是最符合描述这些点的
3.最符合的条件就是这个方程带入所有x计算出的所有y与真实的y值做 均方差计算
4.找到均方差最小的那个w
5.这样就求出了最优解的函数(前提条件是假设b=0)
多参数回归
| 被爱 | 学习指数 | 抗压指数 | 运动指数 | 饮食情况 | 金钱 | 心态 | 压力 | 健康程度 |
|---|---|---|---|---|---|---|---|---|
| 0 | 14 | 8 | 0 | 5 | -2 | 9 | -3 | 339 |
| -4 | 10 | 6 | 4 | -14 | -2 | -14 | 8 | -114 |
| -1 | -6 | 5 | -12 | 3 | -3 | 2 | -2 | 30 |
| 5 | -2 | 3 | 10 | 5 | 11 | 4 | -8 | 126 |
| -15 | -15 | -8 | -15 | 7 | -4 | -12 | 2 | -395 |
| 11 | -10 | -2 | 4 | 3 | -9 | -6 | 7 | -87 |
| -14 | 0 | 4 | -3 | 5 | 10 | 13 | 7 | 422 |
| -3 | -7 | -2 | -8 | 0 | -6 | -5 | -9 | -309 |
| 11 | 14 | 8 | 10 | 5 | 10 | 8 | 1 | ? |
求如果karen的各项指标是:
被爱:11 学习指数:14 抗压指数:8 运动指数:10 饮食水平:5 金钱:10 心态:8 压力:1
那么karen的健康程度是多少?
直接能想到的就是八元一次方程求解:
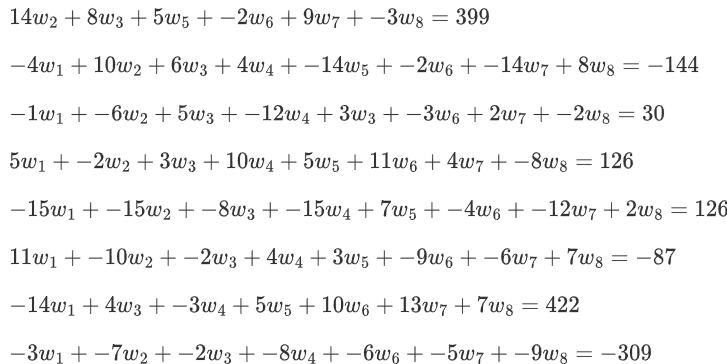
解出 权重 w(w_1,w_2...w_8) 然后带入即可求出karen的健康程度
权重即重要程度,某一项的权重越大说明它影响最终健康的程度越大
但是这有一个前提:这个八元一次方程组得有解才行

最小二乘法
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x0 | y |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 14 | 8 | 0 | 5 | -2 | 9 | -3 | 1 | 339 |
| -4 | 10 | 6 | 4 | -14 | -2 | -14 | 8 | 1 | -114 |
| -1 | -6 | 5 | -12 | 3 | -3 | 2 | -2 | 1 | 30 |
| 5 | -2 | 3 | 10 | 5 | 11 | 4 | -8 | 1 | 126 |
| -15 | -15 | -8 | -15 | 7 | -4 | -12 | 2 | 1 | -395 |
| 11 | -10 | -2 | 4 | 3 | -9 | -6 | 7 | 1 | -87 |
| -14 | 0 | 4 | -3 | 5 | 10 | 13 | 7 | 1 | 422 |
| -3 | -7 | -2 | -8 | 0 | -6 | -5 | -9 | 1 | -309 |

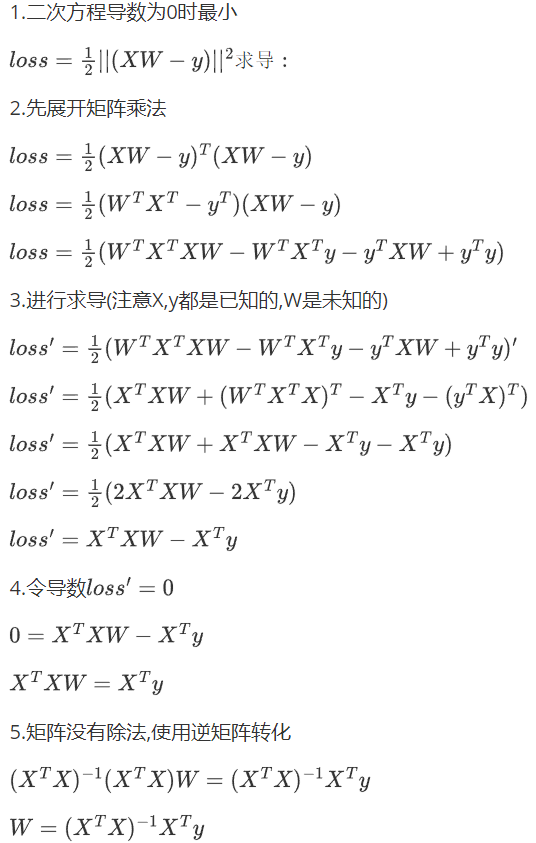

from sklearn.linear_model import LinearRegression
import numpy as np
data=np.array([[0,14,8,0,5,-2,9,-3,399],[-4,10,6,4,-14,-2,-14,8,-144],[-1,-6,5,-12,3,-3,2,-2,30],[5,-2,3,10,5,11,4,-8,126],[-15,-15,-8,-15,7,-4,-12,2,-395],[11,-10,-2,4,3,-9,-6,7,-87],[-14,0,4,-3,5,10,13,7,422],[-3,-7,-2,-8,0,-6,-5,-9,-309]])x=data[:,:-1] #遍历所有行,除了最后一个
y=data[:,-1] #提取一列目标向量
print(x)
print(y)
model=LinearRegression() #创建线性回归模型
model.fit(x,y)
print(model.coef_) #模型系数W
print(model.intercept_) #模型截距b
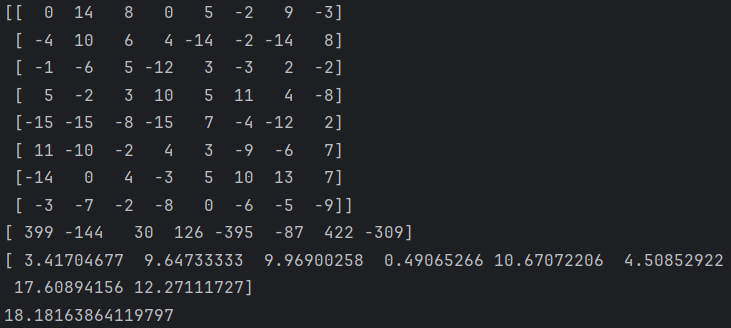
梯度下降
机器学习的损失函数并非都是凸函数,设置导数为0会得到很多个极值,不能确定唯一解,MSE还有一个问题,当数据量和特征较多时,矩阵计算量太大!
1.假设损失函数是这样的,利用正规方程求解导数为0会得到很多个极值,不能确定唯一解
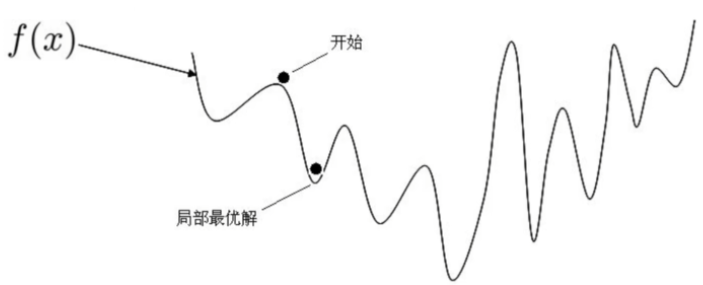
2.使用正规方程![]() 求解要求X的特征维度(x1,x2,x3...) 不能太多,逆矩阵运算时间复杂度为
求解要求X的特征维度(x1,x2,x3...) 不能太多,逆矩阵运算时间复杂度为![]() , 也就是说如果特征x的数量翻倍,计算时间就是原来的2^3倍,8倍太恐怖了,假设2个特征1秒,4个特征8秒,8个特征64秒,16个特征512秒,而往往现实生活中的特征非常多,尤其是大模型,运行时间太长了!
, 也就是说如果特征x的数量翻倍,计算时间就是原来的2^3倍,8倍太恐怖了,假设2个特征1秒,4个特征8秒,8个特征64秒,16个特征512秒,而往往现实生活中的特征非常多,尤其是大模型,运行时间太长了!
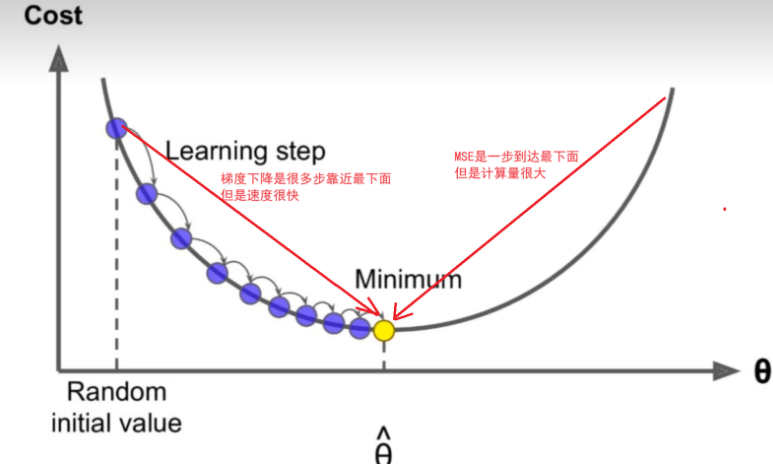
在机器学习中,梯度表示损失函数对于模型参数的偏导数。具体来说,对于每个可训练参数,梯度告诉我们在当前参数值下,沿着每个参数方向变化时,损失函数的变化率。通过计算损失函数对参数的梯度,梯度下降算法能够根据梯度的信息来调整参数,朝着减少损失的方向更新模型,从而逐步优化模型,使得模型性能更好。
在![]() 这个一元二次方程中,损失函数对于参数 w 的梯度就是关于 w 点的切线斜率。梯度下降算法会根据该斜率的信息来调整参数 w,使得损失函数逐步减小,从而找到使得损失最小化的参数值,优化模型的性能。
这个一元二次方程中,损失函数对于参数 w 的梯度就是关于 w 点的切线斜率。梯度下降算法会根据该斜率的信息来调整参数 w,使得损失函数逐步减小,从而找到使得损失最小化的参数值,优化模型的性能。
梯度下降法(Gradient Descent)是一个算法,但不是像多元线性回归那样是一个具体做回归任务的算法,而是一个非常通用的优化算法来帮助一些机器学习算法求解出最优解,所谓的通用就是很多机器学习算法都是用梯度下降,甚至深度学习也是用它来求解最优解。 所有优化算法的目的都是期望以最快的速度把模型参数W求解出来,梯度下降法就是一种经典常用的优化算法。
梯度下降流程就是“猜"正确答案的过程:
1、Random随机数生成初始W,随机生成一组成正太分布的数值W0,W1,W2....Wn,这个随机是成正太分布的(高斯说的)
2、求梯度g,梯度代表曲线某点上的切线的斜率,沿着切线往下就相当于沿着坡度最陡峭的方向下降.
3、if g < 0,w变大,if g >0,w变小(目标左边是斜率为负右边为正 )
4、判断是否收敛,如果收敛跳出迭代,如果没有达到收敛,回第2步再次执行2~4步收敛的判断标准是:随着迭代进行查看损失函数Loss的值,变化非常微小甚至不再改变,即认为达到收敛
5.上面第4步也可以固定迭代次数
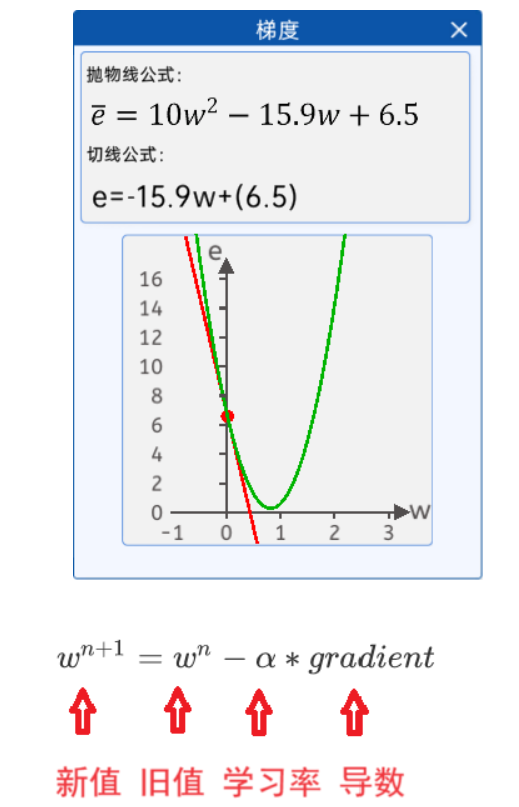
随机给一个w初始值,然后就不停的修改它,直到达到抛物线最下面附近
w=0.2
w=w-0.01*w为0.2时的梯度(导数) 假设算出来是 0.24
w=w-0.01*w为0.24时的梯度(导数) 假设算出来是 0.33
w=w-0.01*w为0.33时的梯度(导数) 假设算出来是 0.51
w=w-0.01*w为0.51时的梯度(导数) 假设算出来是 0.56
w=w-0.01*w为0.56时的梯度(导数) 假设算出来是 0.58
w=w-0.01*w为0.58时的梯度(导数) 假设算出来是 0.62
就这样一直更新下去,会在真实值附近,我们可以控制更新的次数
关于随机的w在左边和右边问题:
因为导数有正负
如果在左边 导数是负数 减去负数就是加 往右移动
如果在右边 导数是正数 减去正数就是减 往左移动
学习率
根据我们上面讲的梯度下降公式,我们知道α是学习率,设置大的学习率α;每次调整的幅度就大,设置小的学习率α;每次调整的幅度就小,然而如果步子迈的太大也会有问题! 学习率大,可能一下子迈过了,到另一边去了(从曲线左半边跳到右半边),继续梯度下降又迈回来,使得来来回回震荡。步子太小呢,就像蜗牛一步步往前挪,也会使得整体迭代次数增加。
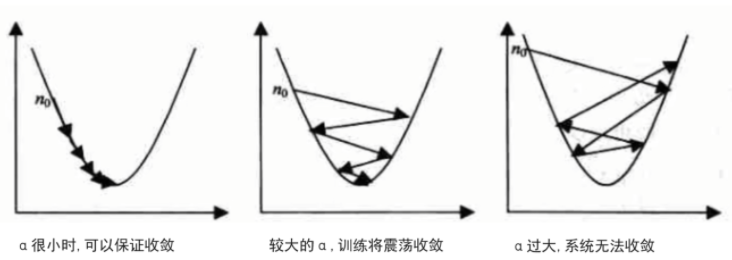
学习率的设置是门一门学问,一般我们会把它设置成一个小数,0.1、0.01、0.001、0.0001,都是常见的设定数值(然后根据情况调整)。一般情况下学习率在整体迭代过程中是不变,但是也可以设置成随着迭代次数增多学习率逐渐变小,因为越靠近山谷我们就可以步子迈小点,可以更精准的走入最低点,同时防止走过。还有一些深度学习的优化算法会自己控制调整学习率这个值。
自己实现梯度下降
import numpy as np
import matplotlib.pyplot as plt
data=np.array([[4.2,3.8],[4.2,2.7],[2.7,2.4],[0.8,1.0],[3.7,2.8],[1.7,0.9],[3.2,2.9]
])
x=data[:,0] # 第一列数据 特征
y=data[:,1] # 第二列数据 标签
print(x)
print(y)
plt.plot(x,y,'o') # 用圆形标记('o')绘制散点图def model(x,w): # 定义线性模型:y = x * w(斜率为w的直线,截距为0)return x*w # 输入x和斜率w,返回预测的y值
def draw_line(w): # 生成0到5之间的100个均匀点作为x轴数据(用于绘制连续直线)point_x=np.linspace(0,5,100)# 根据模型计算对应的y值(y = x * w)point_y=model(point_x,w)plt.plot(point_x,point_y)
draw_line(1) #斜率为1的直线
draw_line(0.5)
plt.show()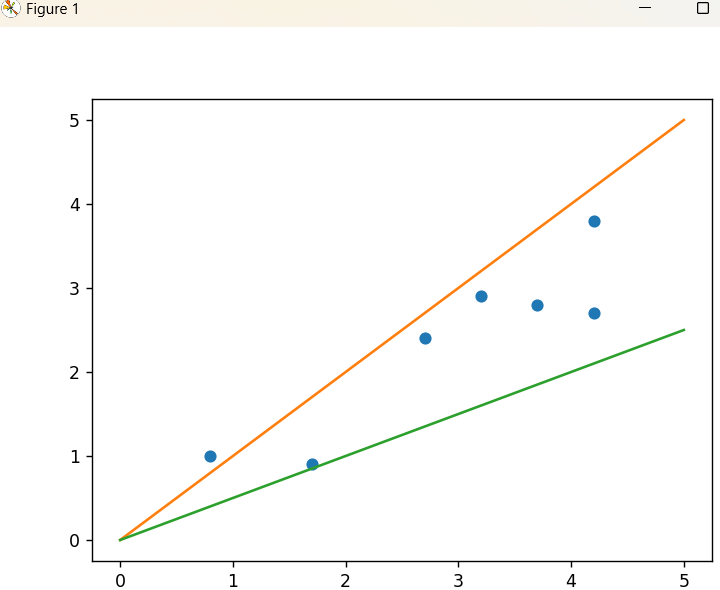
sklearn梯度下降
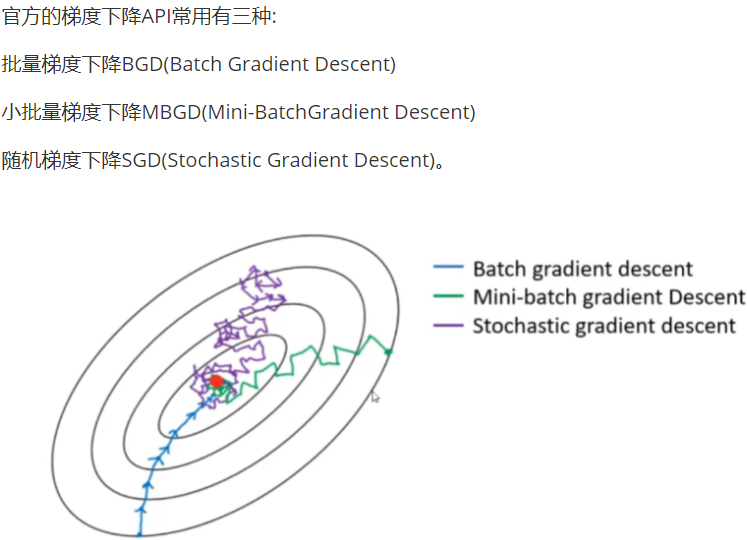
-
Batch Gradient Descent (BGD): 在这种情况下,每一次迭代都会使用全部的训练样本计算梯度来更新权重。这意味着每一步梯度更新都是基于整个数据集的平均梯度。这种方法的优点是每次更新的方向是最准确的,但缺点是计算量大且速度慢,尤其是在大数据集上。
-
Mini-Batch Gradient Descent (MBGD): 这种方法介于批量梯度下降和随机梯度下降之间。它不是用全部样本也不是只用一个样本,而是每次迭代从数据集中随机抽取一小部分样本(例如,从500个样本中选取32个),然后基于这一小批样本的平均梯度来更新权重。这种方法在准确性和计算效率之间取得了一个平衡。
-
Stochastic Gradient Descent (SGD): 在随机梯度下降中,每次迭代仅使用随机单个样本(或有时称为“例子”)来计算梯度并更新权重。这种方法能够更快地收敛,但由于每次更新都基于单个样本,所以会导致权重更新路径不稳定。
批量梯度下降BGD
批量梯度下降是一种用于机器学习和深度学习中的优化算法,它用于最小化损失函数(目标函数)。批量梯度下降使用整个训练数据集来计算梯度并更新模型参数。
原理
批量梯度下降的基本思想是在每个迭代步骤中使用所有训练样本来计算损失函数的梯度,并据此更新模型参数。这使得更新方向更加准确,因为它是基于整个数据集的梯度,而不是像随机梯度下降那样仅基于单个样本。

特点
-
准确性:由于使用了所有训练样本,所以得到的梯度是最准确的,这有助于找到全局最小值。
-
计算成本:每次更新都需要遍历整个数据集,因此计算量较大,特别是在数据集很大的情况下。
-
收敛速度:虽然每一步的更新都是准确的,但由于计算成本较高,实际收敛到最小值的速度可能不如其他方法快。
-
内存需求:需要在内存中存储整个数据集,对于大型数据集来说可能成为一个问题。
使用场景
-
小数据集:当数据集较小时,批量梯度下降是一个不错的选择,因为它能保证较好的收敛性和准确性。
-
不需要实时更新:如果模型不需要实时更新,例如在离线训练场景下,批量梯度下降是一个合理的选择。
实现注意事项
-
选择合适的学习率:选择合适的学习率对于快速且稳定的收敛至关重要。如果学习率太小,收敛速度会很慢;如果太大,则可能会导致不收敛。
-
数据预处理:对数据进行标准化或归一化,可以提高批量梯度下降的效率。
-
监控损失函数:定期检查损失函数的变化趋势,确保算法正常工作并朝着正确的方向前进。
随机梯度下降SGD
随机梯度下降(Stochastic Gradient Descent, SGD)是一种常用的优化算法,在机器学习和深度学习领域中广泛应用。与批量梯度下降(BGD)和小批量梯度下降(MBGD)相比,SGD 每一步更新参数时仅使用单个训练样本,这使得它更加灵活且计算效率更高,特别是在处理大规模数据集时。

注意事项
-
学习率
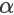 : 需要适当设置,太大会导致算法不收敛,太小则收敛速度慢。
: 需要适当设置,太大会导致算法不收敛,太小则收敛速度慢。 -
随机性: 每次迭代都从训练集中随机选择一个样本,这有助于避免陷入局部最小值。
-
停止条件: 可以是达到预定的最大迭代次数,或者梯度的范数小于某个阈值。
随机梯度下降的一个关键优势在于它能够快速地进行迭代并适应较大的数据集。然而,由于每次只使用一个样本进行更新,梯度估计可能较为嘈杂,这可能导致更新过程中出现较大的波动。在实际应用中,可以通过减少学习率(例如采用学习率衰减策略)来解决这个问题。
小批量梯度下降MBGD
小批量梯度下降是一种介于批量梯度下降(BGD)与随机梯度下降(SGD)之间的优化算法,它结合了两者的优点,在机器学习和深度学习中被广泛使用。
原理
小批量梯度下降的基本思想是在每个迭代步骤中使用一小部分(即“小批量”)训练样本来计算损失函数的梯度,并据此更新模型参数。这样做的好处在于能够减少计算资源的需求,同时保持一定程度的梯度准确性。
特点
-
计算效率:相比于批量梯度下降,小批量梯度下降每次更新只需要处理一部分数据,减少了计算成本。
-
梯度估计:相比于随机梯度下降,小批量梯度下降提供了更准确的梯度估计,这有助于更稳定地接近最小值。
-
内存需求:相比批量梯度下降,小批量梯度下降降低了内存需求,但仍然比随机梯度下降要高。
-
收敛速度与稳定性:小批量梯度下降能够在保持较快的收敛速度的同时,维持相对较高的稳定性。
使用场景
-
中等规模数据集:当数据集大小适中时,小批量梯度下降是一个很好的折衷方案,既能够高效处理数据,又能够保持良好的收敛性。
-
在线学习:在数据流式到达的场景下,小批量梯度下降可以有效地处理新到来的数据批次。
-
分布式环境:在分布式计算环境中,小批量梯度下降可以更容易地在多台机器上并行执行。
实现注意事项
-
选择合适的批量大小:批量大小的选择对性能有很大影响。较大的批量可以减少迭代次数,但计算成本增加;较小的批量则相反。
-
选择合适的学习率:选择合适的学习率对于快速且稳定的收敛至关重要。如果学习率太小,收敛速度会很慢;如果太大,则可能会导致不收敛。
-
数据预处理:对数据进行标准化或归一化,可以提高小批量梯度下降的效率。
-
监控损失函数:定期检查损失函数的变化趋势,确保算法正常工作并朝着正确的方向前进。
欠拟合和过拟合
欠拟合
欠拟合是指模型在训练数据上表现不佳,同时在新的未见过的数据上也表现不佳。这通常发生在模型过于简单,无法捕捉数据中的复杂模式时。欠拟合模型的表现特征如下:
-
训练误差较高。
-
测试误差同样较高。
-
模型可能过于简化,不能充分学习训练数据中的模式。
过拟合
过拟合是指模型在训练数据上表现得非常好,但在新的未见过的数据上表现较差。这通常发生在模型过于复杂,以至于它不仅学习了数据中的真实模式,还学习了噪声和异常值。过拟合模型的表现特征如下:
-
训练误差非常低。
-
测试误差较高。
-
模型可能过于复杂,以至于它对训练数据进行了过度拟合。
正则化
正则化就是防止过拟合,增加模型的鲁棒性,鲁棒是Robust 的音译,也就是强壮的意思。就像计算机软件在面临攻击、网络过载等情况下能够不死机不崩溃,这就是软件的鲁棒性,鲁棒性调优就是让模型拥有更好的鲁棒 性,也就是让模型的泛化能力和推广能力更加的强大。
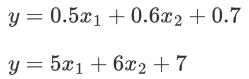
第一个更好,因为下面的公式是上面的十倍,当w越小公式的容错的能力就越好。我们都知道人工智能中回归是有误差的,为了把误差降低而拟合出来的一个接近真实的公式,比如把一个测试数据[10,20]带入计算得到的值跟真实值会存在一定的误差,但是第二个方程会把误差放大,公式中![]() ,当x有一点错误,这个错误会通过w放大。但是w不能太小,当w太小时(比如都趋近0),模型就没有意义了,无法应用。想要有一定的容错率又要保证正确率就要由正则项来发挥作用了! 所以正则化(鲁棒性调优)的本质就是牺牲模型在训练集上的正确率来提高推广、泛化能力,W在数值上越小越好,这样能抵抗数值的扰动。同时为了保证模型的正确率W又不能极小。因此将原来的损失函数加上一个惩罚项使得计算出来的模型W相对小一些,就是正则化。这里面损失函数就是原来固有的损失函数,比如回归的话通常是MSE,然后在加上一部分惩罚项来使得计算出来的模型W相对小一些来带来泛化能力。
,当x有一点错误,这个错误会通过w放大。但是w不能太小,当w太小时(比如都趋近0),模型就没有意义了,无法应用。想要有一定的容错率又要保证正确率就要由正则项来发挥作用了! 所以正则化(鲁棒性调优)的本质就是牺牲模型在训练集上的正确率来提高推广、泛化能力,W在数值上越小越好,这样能抵抗数值的扰动。同时为了保证模型的正确率W又不能极小。因此将原来的损失函数加上一个惩罚项使得计算出来的模型W相对小一些,就是正则化。这里面损失函数就是原来固有的损失函数,比如回归的话通常是MSE,然后在加上一部分惩罚项来使得计算出来的模型W相对小一些来带来泛化能力。
常用的惩罚项有L1正则项或者L2正则项:
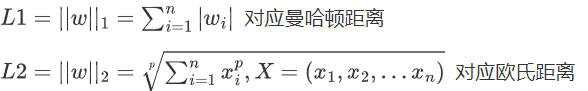
其实L1 和L2 正则的公式在数学里面的意义就是范数,代表空间中向量到原点的距离
当我们把多元线性回归损失函数加上L2正则的时候,就诞生了Ridge岭回归。当我们把多元线性回归损失函数加上L1正则的时候,就孕育出来了Lasso回归。其实L1和L2正则项惩罚项可以加到任何算法的损失函数上面去提高计算出来模型的泛化能力的。
岭回归Ridge
岭回归是失损函数通过添加所有权重的平方和的乘积(L2)来惩罚模型的复杂度。
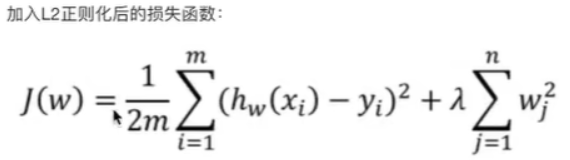
均方差除以2是因为方便求导,w_j指所有的权重系数, λ指惩罚型系数,又叫正则项力度
特点:
-
岭回归不会将权重压缩到零,这意味着所有特征都会保留在模型中,但它们的权重会被缩小。
-
适用于特征间存在多重共线性的情况。
-
岭回归产生的模型通常更为平滑,因为它对所有特征都有影响。
from sklearn.linear_model import Ridge
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_errorx,y=fetch_california_housing(return_X_y=True,data_home="(自己的当前文件目录下,如./src,当前文件下的src文件夹)")
# 划分数据集,20%作为测试集,固定随机种子保证结果复现
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=42)
scaler=StandardScaler()
x_train=scaler.fit_transform(x_train)
x_test=scaler.transform(x_test)
#正则化强度alpha,最大迭代次数max_iter,是否计算截距项fit_intercept
model=Ridge(alpha=0.1,max_iter=100,fit_intercept=True) #更改权重时,过小导致过拟合,过大导致欠拟合
#训练数据得到特征与目标值的关系
model.fit(x_train,y_train)
y_hat=model.predict(x_test)print("loss:",mean_squared_error(y_test,y_hat)) #均方误差MSE
print("w:",model.coef_) #输出每个特征的权重
print("b:",model.intercept_) #输出截距项拉索回归Lasso
Lasso回归是一种线性回归模型,它通过添加所有权重的绝对值之和(L1)来惩罚模型的复杂度。
Lasso回归的目标是最小化以下损失函数:
![]()
其中:
-
n 是样本数量,
-
p 是特征的数量,
-
yi 是第 i 个样本的目标值,
-
xi 是第 i 个样本的特征向量,
-
w是模型的参数向量,
-
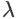 是正则化参数,控制正则化项的强度。
是正则化参数,控制正则化项的强度。
特点:
-
拉索回归可以将一些权重压缩到零,从而实现特征选择。这意味着模型最终可能只包含一部分特征。
-
适用于特征数量远大于样本数量的情况,或者当特征间存在相关性时,可以从中选择最相关的特征。
-
拉索回归产生的模型可能更简单,因为它会去除一些不重要的特征。
from sklearn.datasets import fetch_california_housing #需fetch联网加载数据集哦
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np# 加载波士顿房价数据集
data = fetch_california_housing(data_home="./src")
X, y = data.data, data.target
# 划分训练集和测试集
X_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建Lasso回归模型
lasso = Lasso(alpha=0.1) # alpha是正则化参数
# 训练模型
lasso.fit(X_train, y_train)
# 得出模型
print("权重系数为:\n", lasso.coef_) #权重系数与特征数一定是同样的个数。
print("偏置为:\n", lasso.intercept_)#模型评估
y_predict = lasso.predict(x_test)
print("预测的数据集:\n", y_predict)
error = mean_squared_error(y_test, y_predict)
print("均方误差为:\n", error)十三、逻辑回归
概念
逻辑回归(Logistic Regression)是机器学习中的一种分类模型,逻辑回归是一种分类算法,虽然名字中带有回归,但是它与回归之间有一定的联系。由于算法的简单和高效,在实际中应用非常广泛。
逻辑回归一般用于二分类问题,比如:
是好瓜还是坏瓜
健康还是不健康
可以托付终身还是不可以
原理
逻辑回归的输入是线性回归的输出
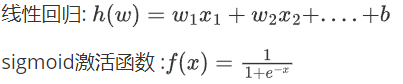
sigmoid函数的值是在[0,1]区间中的一个概率值,默认0.5为阈值可以自己设定,大于0.5认为是正例,小于则认为是负例
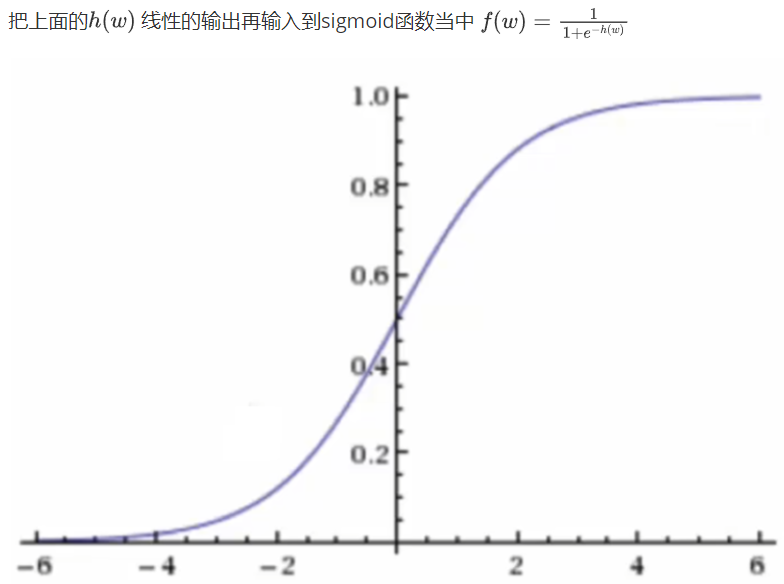
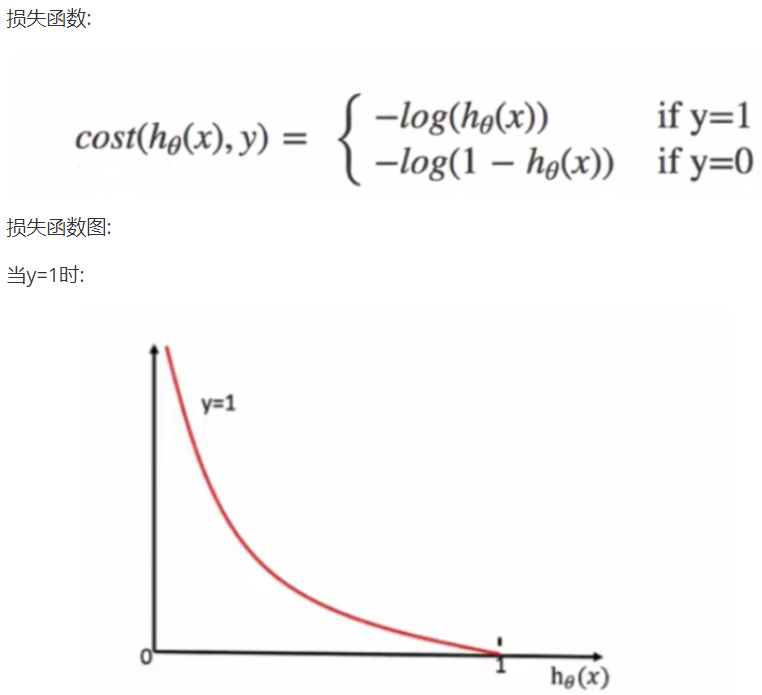
通过损失函数图像,我们知道:
当y=1时,我们希望![]() 值越大越好
值越大越好
当y=0时,我们希望![]() 值越小越好
值越小越好
综合0和1的损失函数:
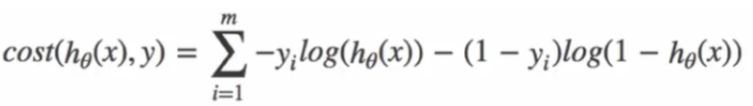
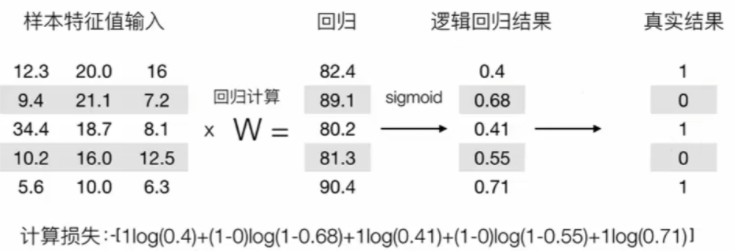
逻辑回归结果即是属于真实结果这个类的概率,如第一条,是1这个类的概率为0.4 (主要),是0的概率则为 ( 1 - 0.4 )
然后使用梯度下降算法,去减少损失函数的值,这样去更新逻辑回归前面对应算法的权重参数,提升原本属于1类别的概率,降低原本是0类别的概率.
from sklearn.linear_model import LogisticRegression
import pandas as pd
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
data=pd.read_csv("./src/titanic/titanic.csv")
print(data.columns) #打印所有列名y=data["survived"].values #提取survived列数据作为目标向量
print(y.dtype)x=data[["pclass","age","sex"]]
x[["age"]].fillna(x[["age"]].mean(),inplace=True) #对age列缺失值用众数进行填充
# x["age"].fillna(x["age"].mean(),inplace=True)
x[["sex"]].fillna(x[["sex"]].mode(),inplace=True) #对sex列缺失值用众数进行填充
# x["sex"].fillna(x["sex"].mode(),inplace=True)#将特征转换为字典列表
x=x.to_dict(orient="records")
dicter=DictVectorizer(sparse=False) #初始化DictVectorizer(将类别特征转换为数值特征)
x=dicter.fit_transform(x)
#获取特征名称
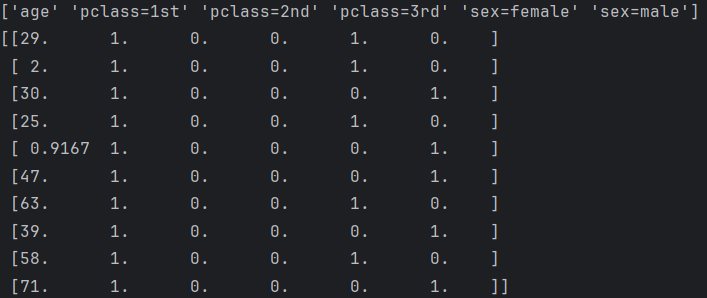
print(dicter.get_feature_names_out())
print(x[:10])#拆分数据集,20%测试集,固定随机种子保证结果复现
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=42)
#初始化标准化器
scaler=StandardScaler()
x_train=scaler.fit_transform(x_train) # 拟合训练集并标准化
x_test=scaler.transform(x_test) # 用训练集的规则标准化测试集# 迭代1000次确保收敛,次数少可能无法收敛
model=LogisticRegression(max_iter=1000,fit_intercept=True)
model.fit(x_train,y_train) #用训练集训练模型
score=model.score(x_test,y_test) #计算测试集上的准确率
print("score:",score)注意:需要在当前代码的目录下有.src文件夹且文件夹中需要有titannic数据集
十四、无监督之K-Means算法
无监督学习
-
无监督学习(Unsupervised Learning)计算机根据样本的特征或相关性,实现从样本数据中训练出相应的预测模型
-
无监督学习模型算法中,模型只需要使用特征矩阵X即可,不需要真实的标签y,聚类算法是无监督学习中的代表之一
-
聚类算法:
-
数据集中,拥有数据特征,但是没有具体的标签
-
将数据划分成有意义或有用的簇
-
聚类算法追求“簇内差异小,簇外差异大”。而这个 “差异”便是通过样本点到其簇质心的距离来衡量
-
-
聚类算法和分类算法的区别:
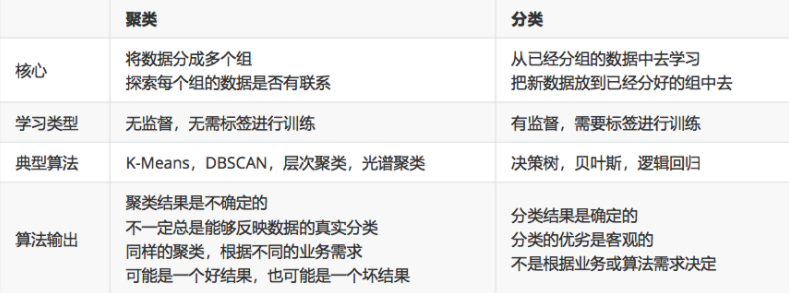
K-means算法
K-means 是一种流行的聚类算法,主要用于无监督学习中对未标记的数据进行分类。该算法的目标是将数据集中的样本划分为K个簇,使得簇内的样本彼此之间的差异最小化。这种差异通常通过簇内所有点到该簇中心点的距离平方和来衡量

K-means 算法的基本步骤:
-
随机抽取
k个样本作为最初的质心,这可以通过随机选取数据集中的K个样本或者使用一些启发式方法来实现 -
计算每个样本点与
k个质心的距离(通常是欧氏距离),将样本点分配到最近的一个质心,生成k个簇 -
对于每个簇,计算所有被分该簇的样本点的平均值作为新的质心
-
当质心的位置不再发生变化或者迭代结束,聚类完成
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
np.random.seed(42)
data=np.random.randint(0,100,(300,2))
# print(data)#创建KMeans模型 设定簇数量为3,则分为三块不同颜色区域
model=KMeans(n_clusters=3)
#训练模型
model.fit(data)
print(model.labels_)
print(model.cluster_centers_)
#提取样本中的数据分别作为x,y轴
x=data[:,0]
y=data[:,1]
#scatter画点 plot画线 c=model.labels_表示根据聚类标签设置点的颜色
plt.scatter(x,y,c=model.labels_)
plt.show()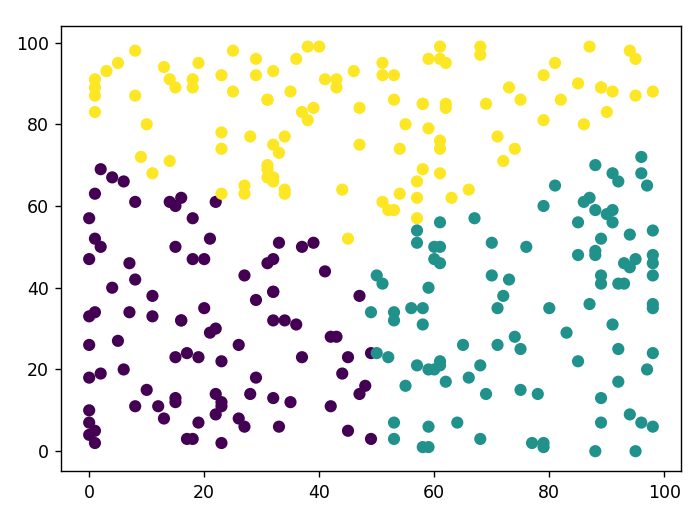
总结
综上就是此次关于机器学习的所有内容啦,希望阅读后能对您有所帮助,那是我的荣辛!如果还有疑问,欢迎在评论区提出哦,我会第一时间尽力帮大家解决。谢谢!