机器学习算法系列专栏:决策树算法(初学者)
(一)决策树概念
决策树通过对训练样本的学习,并建立分类规则然后依据分类规则,对新样本数据进行分类预测,属于有监督学习
(二)决策树核心
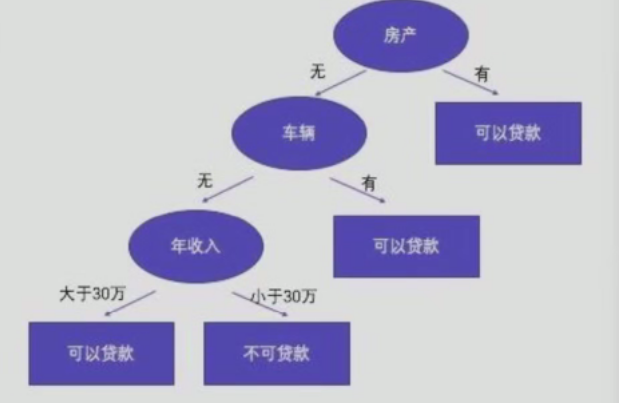
所有数据从根节点一步一步落到叶子节点
- 根节点:第一个节点
- 非叶子节点:中间节点
- 叶子节点:最终结果节点
(三)常见问题
1.哪个节点作为根节点?哪些节点作为中间节点?哪些节点作为叶子节点 ?
根节点:由算法根据全局最优特征自动选择
中间节点:由算法在满足分裂条件时递归生成
叶子节点:由算法在满足停止条件时自动标记,存储最终预测结果
关键点:决策树的节点角色完全由数据和算法规则决定,无需人工干预
2.节点如何分裂 ?
在当前节点上,选择一个最优特征和一个最优切分点,把样本分到左右(或多路)子节点中,使得子节点的纯度最高(不纯度最低)
3.节点分裂标准的依据 ?
使分裂后子节点的“不纯度下降”最大(或等价地,使子节点纯度提高最多)
不同决策树算法只是用不同的数学指标来量化“不纯度下降”,而具体用哪个指标取决于你选的是 ID3、C4.5 还是 CART
(四)决策树分类标准
1.ID3算法 ― 信息增益 (Information Gain)
衡量标准:
熵值:表示随机变量不确定性的度量,或者说是物体内部的混乱程度
熵值计算公式:
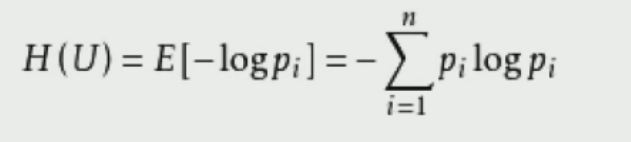
A集合:[1,1,1,1,1,1,1,1,2,2]
B集合:[0,1,2,3,4,5,6,7,8,9]
A集合熵值:-2/10*log2(2/10)-8/10*log2(8/10)= 0.722
B集合熵值:-1/10*log2(1/10)*10= 3.322
显然B的熵值更大,更加混乱

2.C4.5算法 ― 信息增益比 (Gain Ratio)
衡量标准:信息增益率

3.CART决策树― Gini 指数下降 (分类树) 或 MSE 下降 (回归树)

(五)决策树剪枝
(5.1)剪枝原因
防止过拟合
(5.2)剪枝方法
预剪枝和后剪枝
(5.3)预剪枝策略
- 限制树的深度
- 限制叶子节点的个数以及叶子节点的样本数
- 基尼系数
(六)决策树的回归模型
(6.1)回归树概念
解决回归问题的决策树模型即为回归树
(6.2)回归树特点
必须是二叉树
(6.3)回归树实现步骤
(1)计算最优切分点

因为只有一个变量,所以切分变量必然是x
可以考虑如下9个切分点:[1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5]
原因:实际上考虑两个变量间任意一个位置为切分点均可
切分点1.5的计算
当s=1.5时,将数据分为两个部分:
第一部分:(1,5.56)
第二部分:(2,5.7)、(3,5.91)、(4,6.4)...(10,9.05)
核心:
1.节点切分依据?
使分裂后左右子节点的“均方误差(MSE)下降”最大
2.如何预测?
预测时,把待预测样本沿树一路分到某个叶子节点,用该叶子节点内训练样本的目标值均值作为输出
(2)计算损失
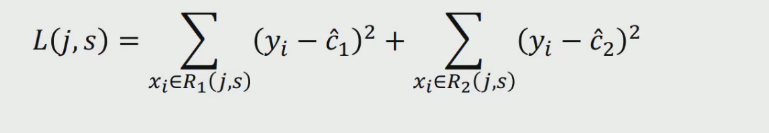
C1=5.56
C2=1/9(5.7+5.91+6.4+6.8+7.05+8.9+8.7+9+9.05)=7.5
Loss =(5.56-5.56)^2+(5.7-7.5)^2+(5.91-7.5)^2+...+(9.05-7.5)^2=0+15.72=15.72
(3)同理计算其他分割点的损失

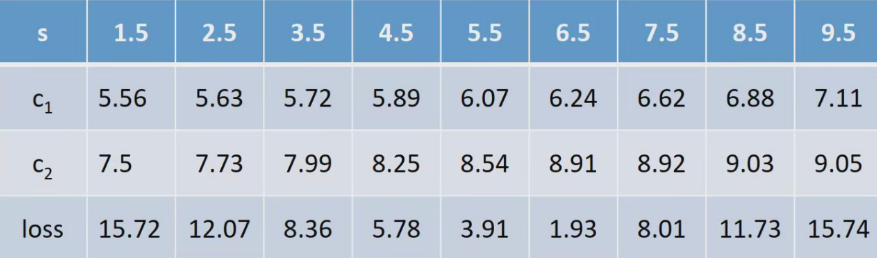
容易看出,当s=6.5时,loss=1.93最小,所以第一个划分点s=6.5
(4)对于小于6.5部分

切分点1.5的计算
当s=1.5时,将数据分为两个部分,第一部分:(1,5.56)第二部分:(2,5.7)、(3,5.91)、(4,6.4),(5,6.8)、(6,7.05)
C =5.56
C,=1/5(5.7+5.91+6.4+6.8+7.05)=6.37Loss =0+(5.7-6.37)^2+(5.91-6.37)^2+..+(7.05-6.37)^2=0+13087=13087
(5)因此得到:

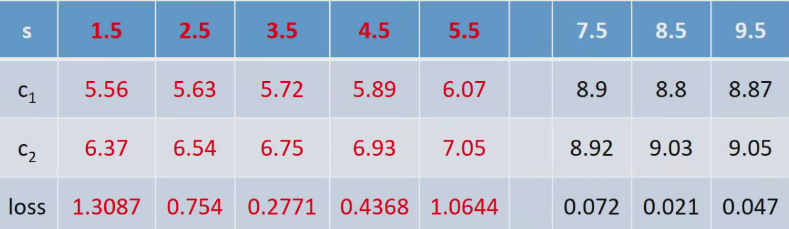
容易看出:
- 当s=3.5时,loss=0.2771最小,所以第一个划分点s=3.5
- 当s=8.5时,ioss=0.021最小,所以第二个划分点s=8.5
(6)假设只分裂我们计算的这几次:

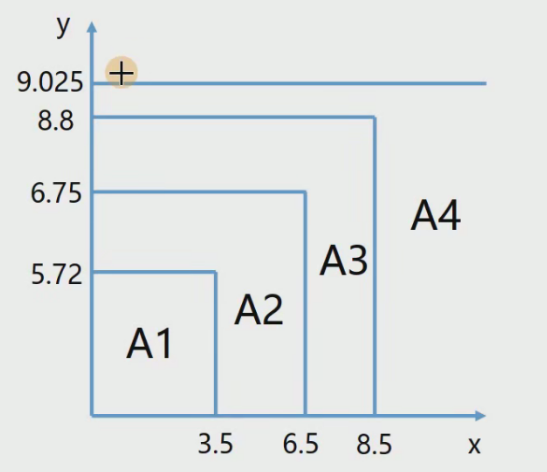
那么分段函数为:
- 当x<=3.5时,1/3(5.56+5.7+5.91)=5.72
- 当3.5<x<=6.5时,1/3(6.4+6.8+7.05)=6.75
- 当6.5<x<=8.5时,1/2(8.9+8.7)=8.8
- 当8.5<x时,1/2(9+9.05)=9.025
最终得到分段函数!
(7)对于预测来说:
特征x必然位于其中某个区间内,所以,即可得到回归的结果,比如说:
如果x=11,那么对应的回归值为9.025
- 当x<=3.5时,1/3(5.56+5.7+5.91)=5.72
- 当3.5<x<=6.5时,1/3(6.4+6.8+7.05)=6.75
- 当6.5<x<=8.5时,1/2(8.9+8.7)=8.8
- 当8.5<x时,1/2(9+9.05)=9.025
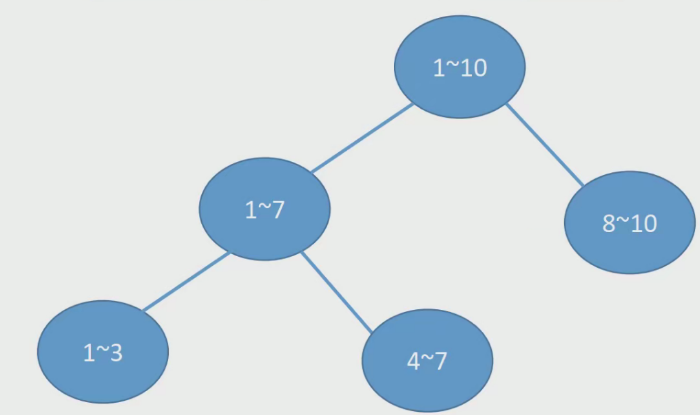
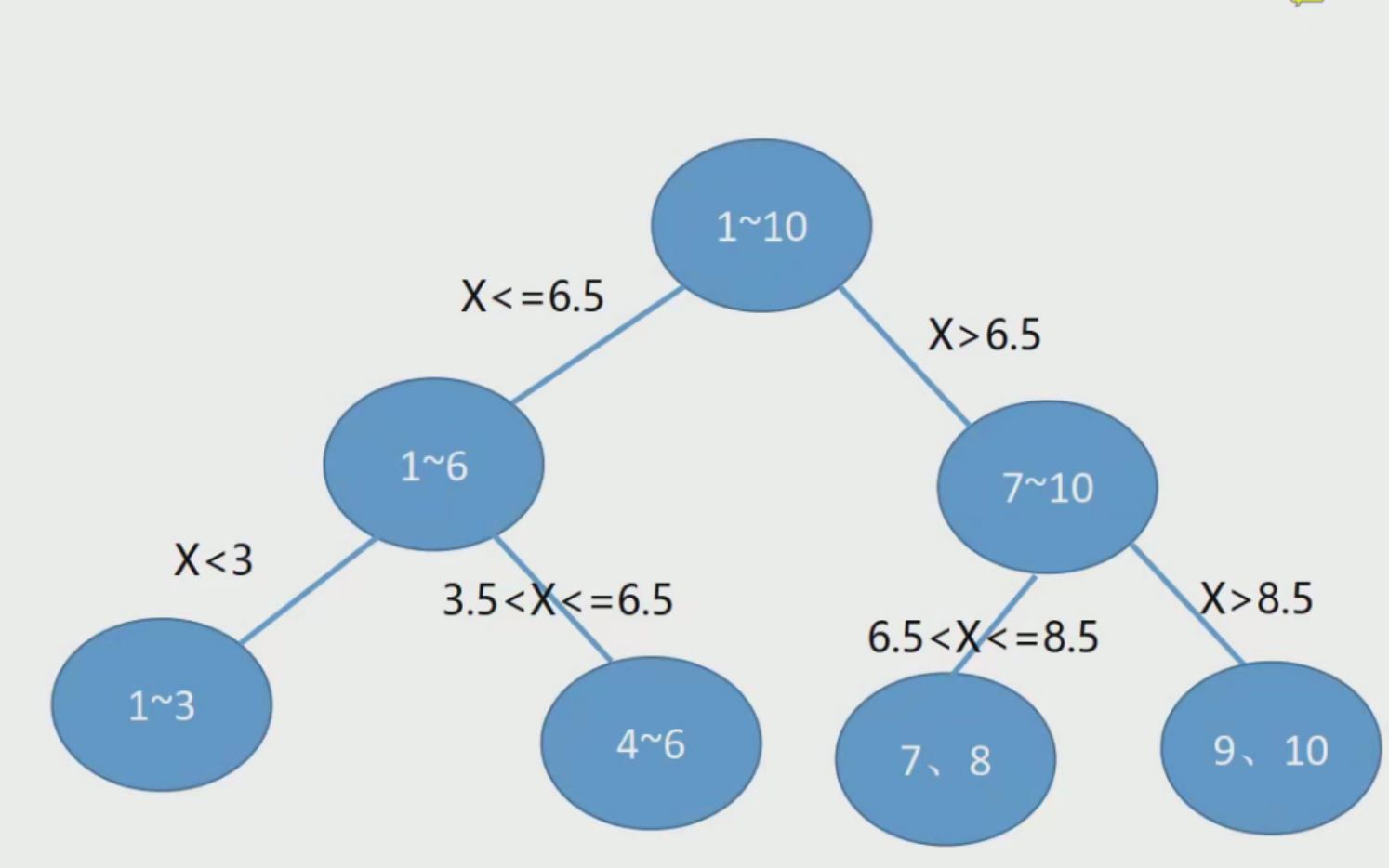
(8)决策树的构造:
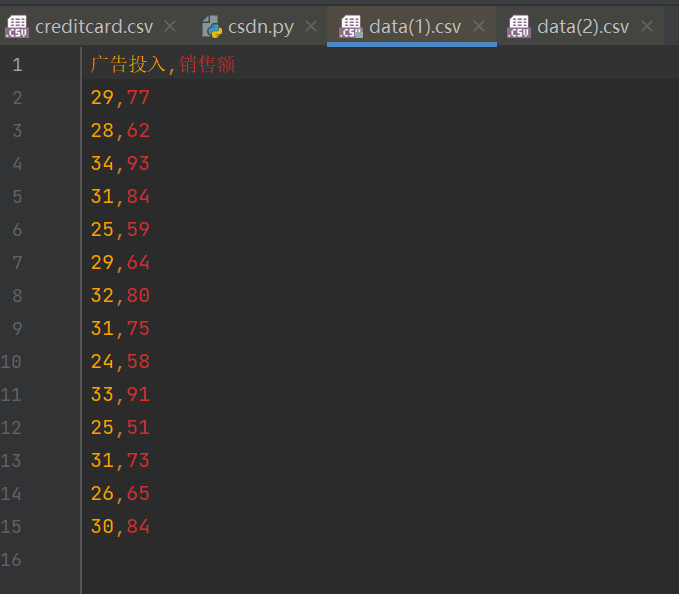
(六)具体代码实现案例
import pandas as pd
from sklearn import treedata = pd.read_csv("data(1).csv")x = data.iloc[:, :-1]
y = data.iloc[:, -1]reg = tree.DecisionTreeRegressor()
reg = reg.fit(x, y)y_pr = reg.predict(x)
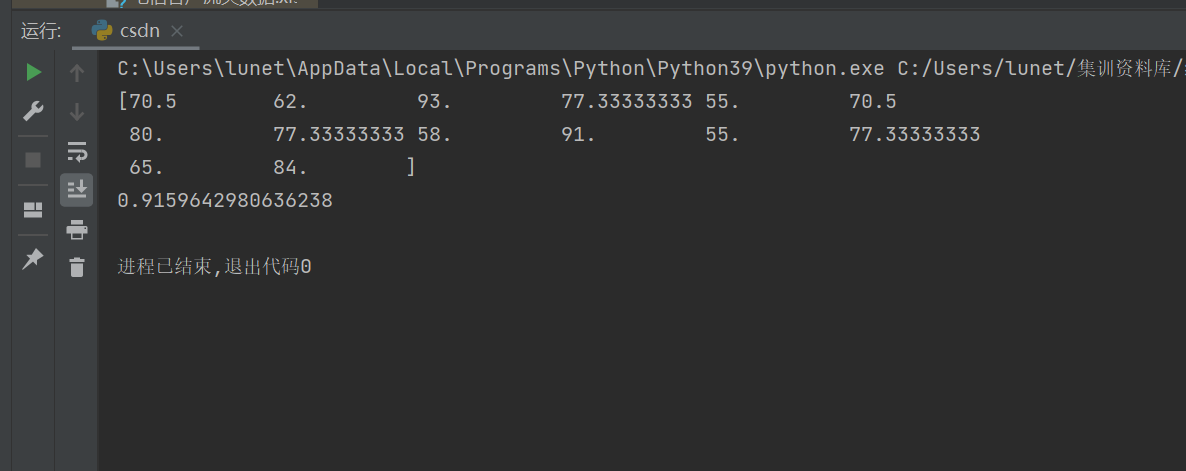
print(y_pr)
score = reg.score(x, y)
print(score)