内部排序算法总结(考研向)
内部排序算法总结
- 排序总览
- 插入排序
- 直接插入排序
- 效率分析
- 折半插入排序
- 效率分析
- 希尔排序(缩小增量排序)
- 交换排序
- 冒泡排序
- 效率分析
- 快速排序(枢轴)
- 效率分析
- 选择排序
- 简单选择排序
- 效率分析
- 堆排序
- 建堆
- 排序
- 效率分析
- 归并排序
- 效率分析
- 基数排序
- 分配
- 收集
- 效率分析
排序总览
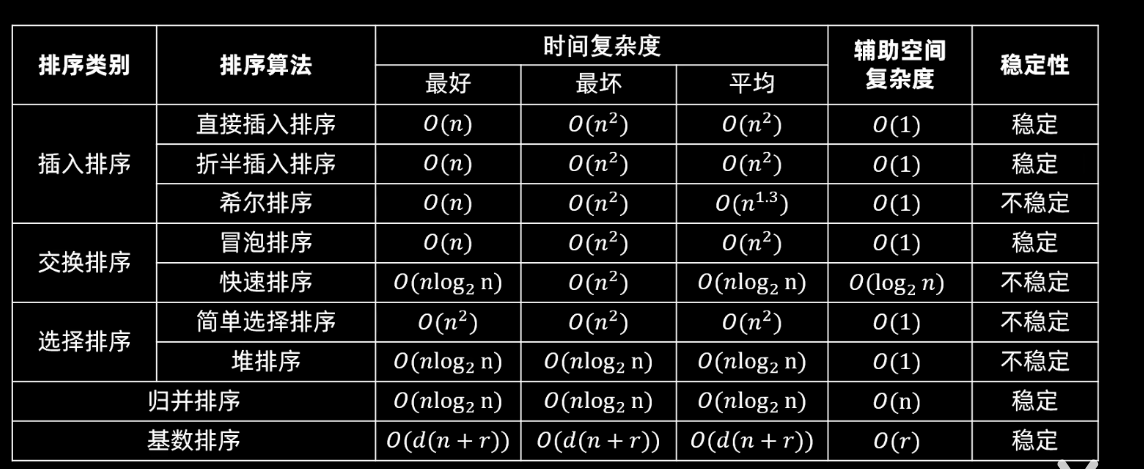
插入排序
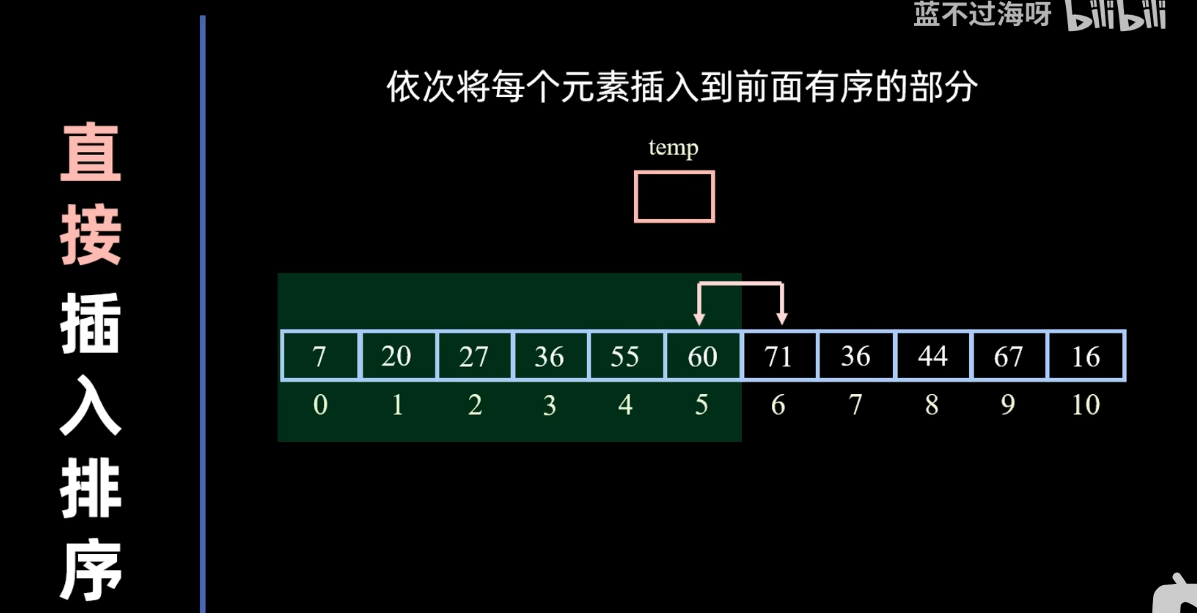
直接插入排序
- 其实这种排序非常简单就是设置一个temp变量用于存储我们欲排序的元素 然后去依次进行比较
- 特别的 若我们当前欲排序的元素比前面 从小到大排好序列的最后一个元素 都大 此时就不需要进行移动 此时将它视为扩充序列里的最大元素 理应放在最后对吧
- 一般的 我们就是一个一个比较只要temp<当前比较的元素就需要继续向前比较 同时说明我们当前比较的元素不该在这个位置 就向后移动腾出位置
效率分析

折半插入排序
- 其实听名字就能感觉这个排序要高级一点儿 说白了这个比上面的直接插入排序在找插入位置的时候要聪明一点
- 不妨假设我们当前有1000…(此处省略一万个0)个数 我们折半查找的优势在找插入位置的时候的优势就非常明显 虽然不能改变移动次数(由于数组的特性 每次插入 后面所有元素都得相应后退一个位置)
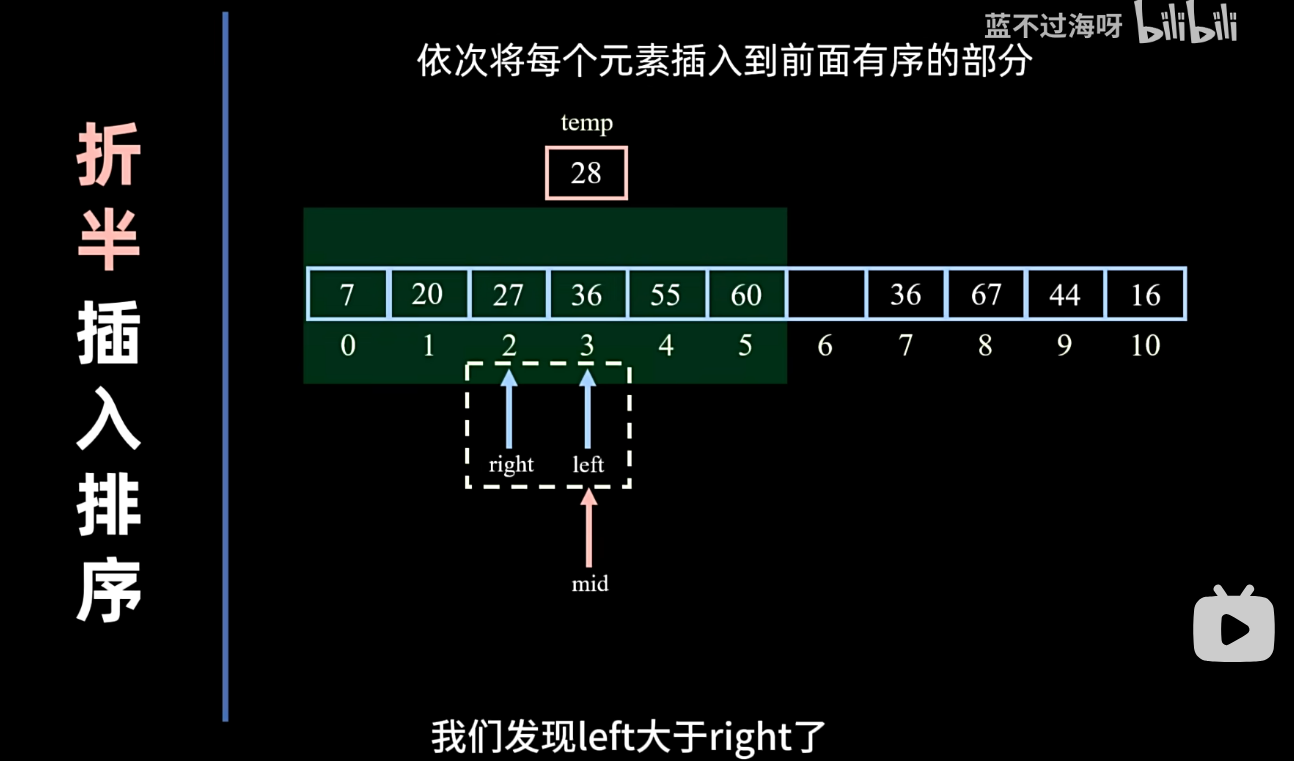
- 回顾我们的折半(二分)查找 while循环的退出条件是不是就是 left < right
效率分析

希尔排序(缩小增量排序)
- 这个其实也是非常好理解的 本质上就是将一个大的数组按照统一的一个标准进行分组 我们不断地去让组内有序 随着这个标准卡的越来越严格(d减到1)我们整体的数组也有序了

交换排序
冒泡排序
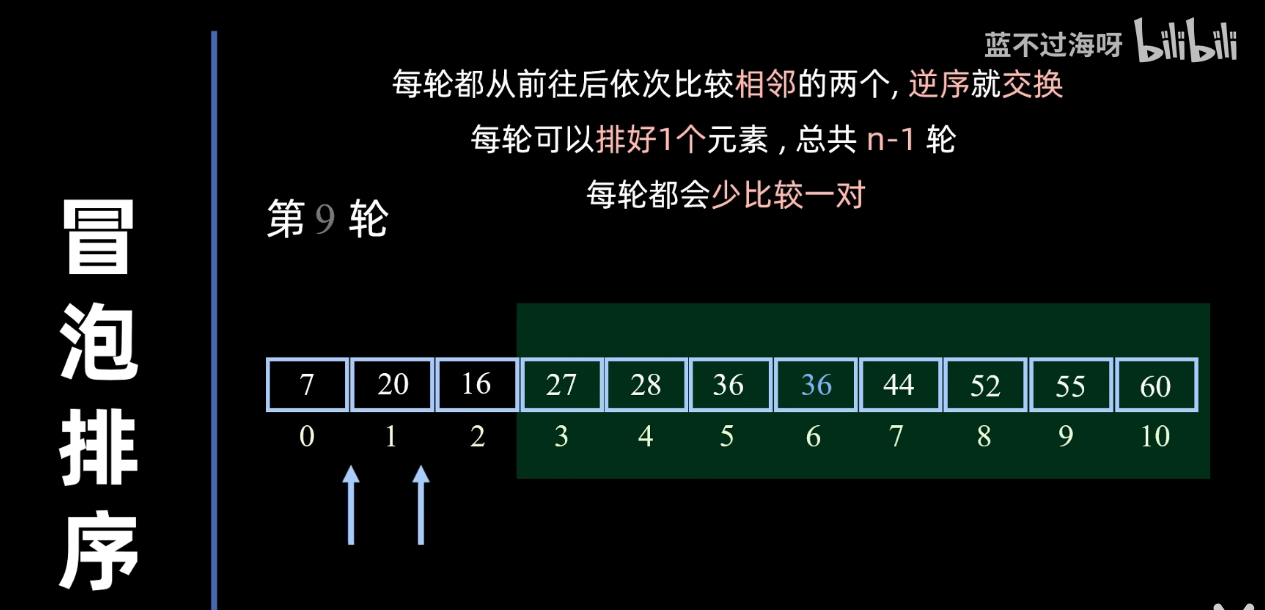
效率分析

快速排序(枢轴)
就是快!
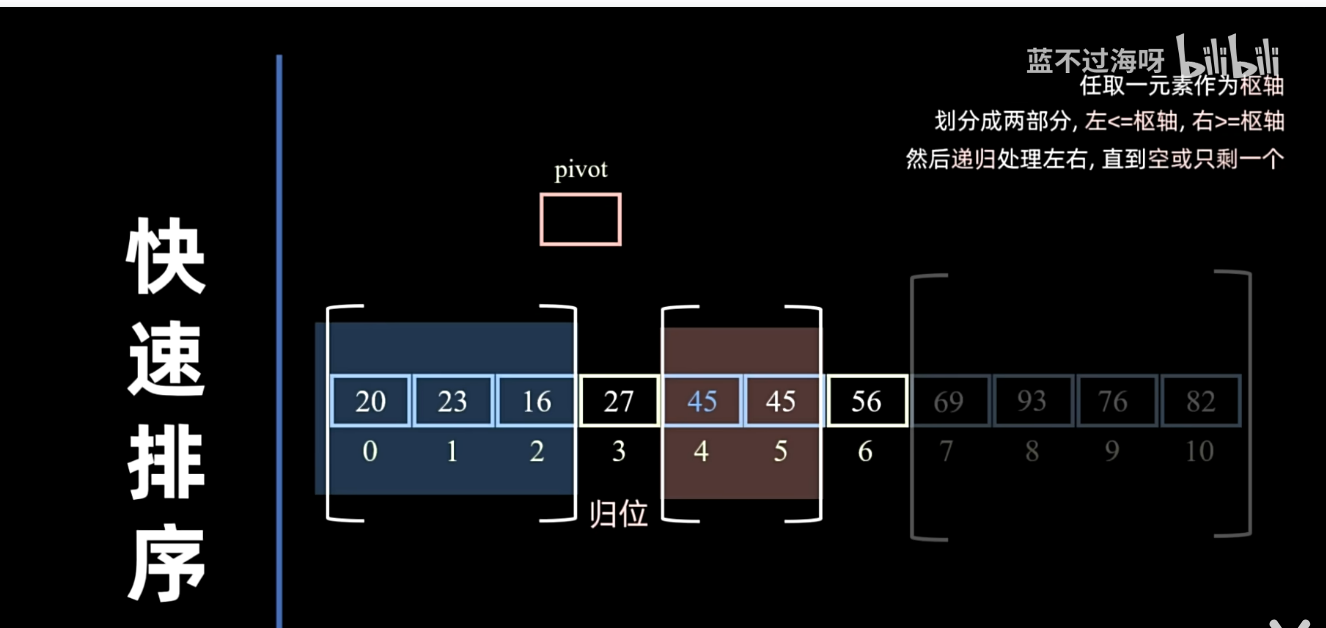
效率分析

选择排序
简单选择排序
每次遍历数组选中最小的元素 与当前数组最后一个元素进行交换(把他放在最终位置上)

效率分析

堆排序
建堆
一句话总结 就是从最后一个非叶节点开始(因为叶子节点本身已经是堆了)检查是否符合大根堆的性质——父节点>=子节点
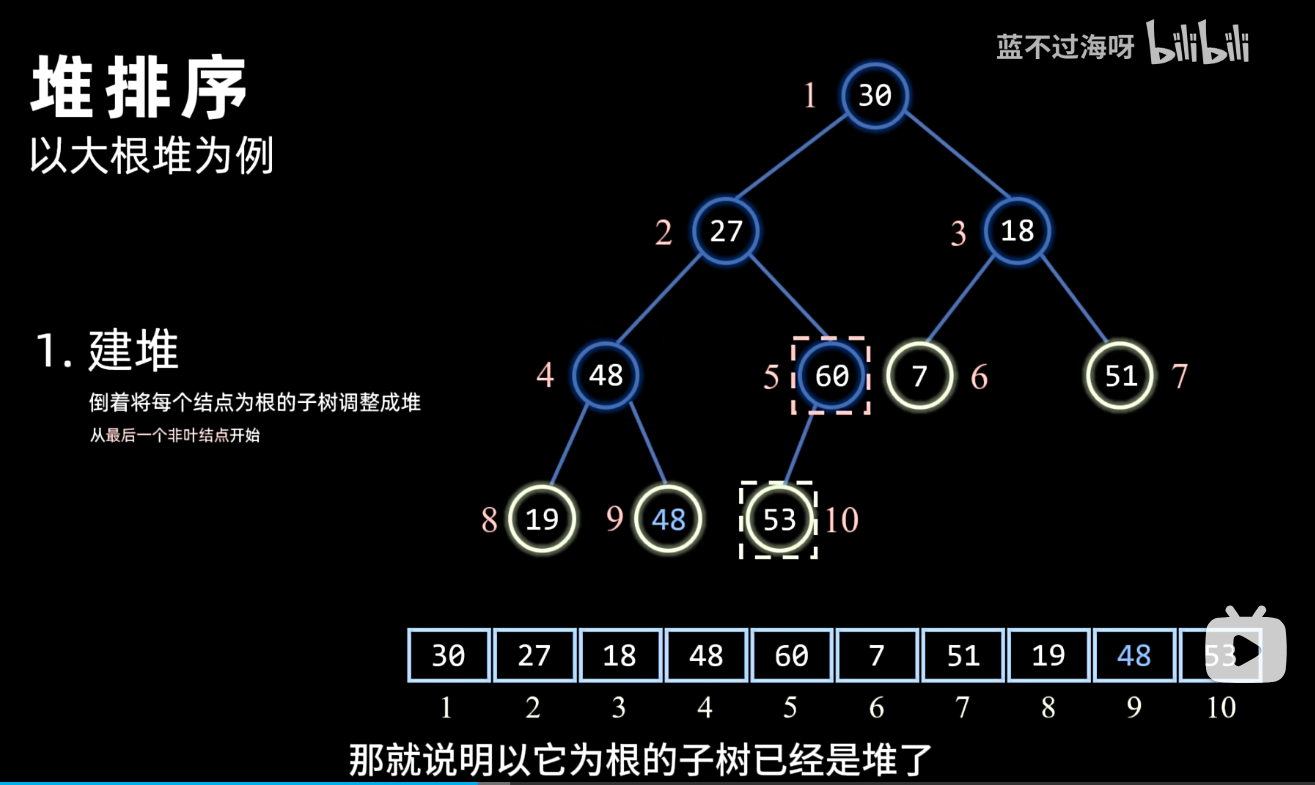
排序
每一次取最大值 即根节点(大根堆情况) 根最后元素交换 然后在逻辑结构上删去排好序的元素 然后调整 再重复上面的流程 但是整个排序实际上是在数组上利用交换完成的 我们建立的二叉树只是逻辑结构 并不是额外创建的辅助空间
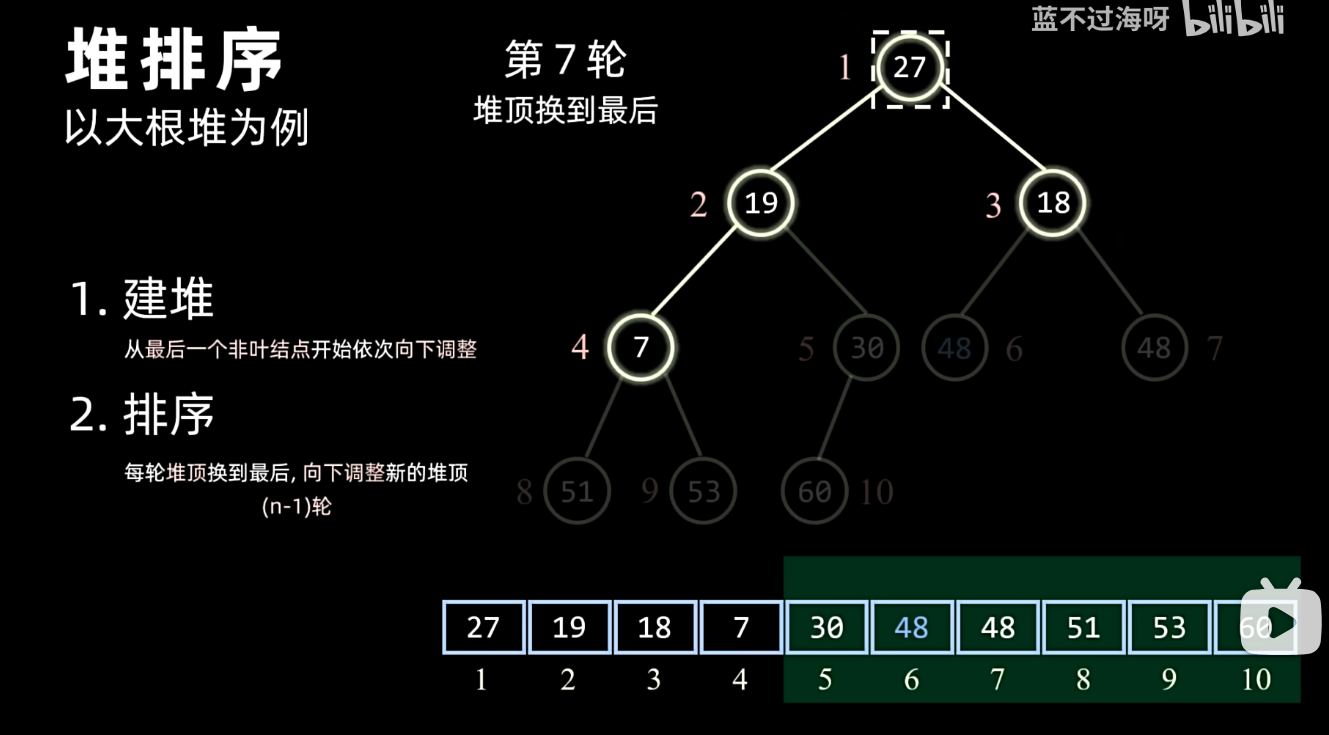
效率分析

归并排序
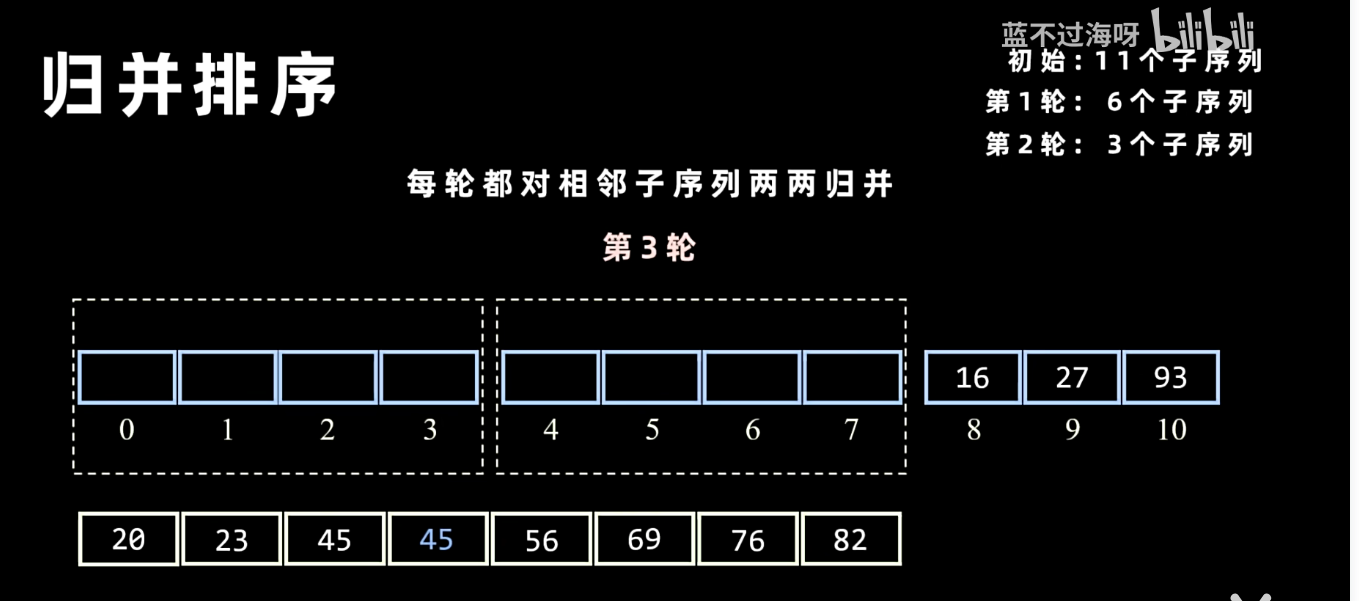
效率分析

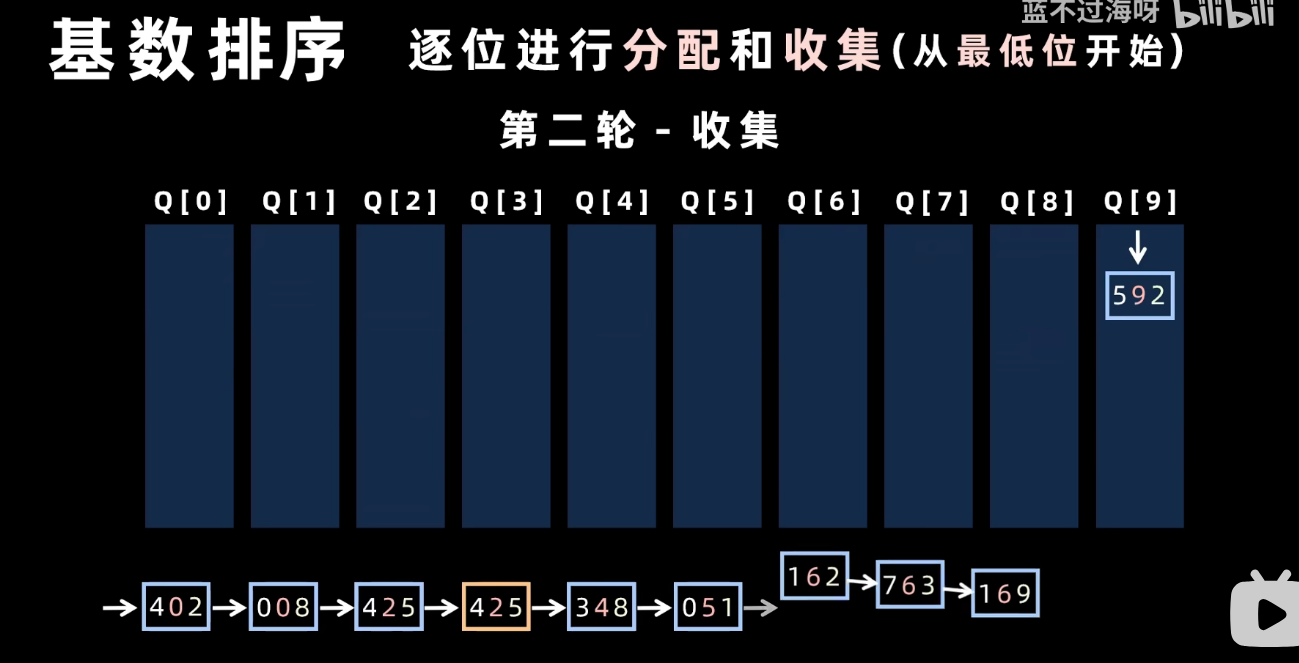
基数排序
- 这个大哥跟前面我们所有介绍的排序都不一样 因为他根本都不存在元素的比较
分配

收集
效率分析

