永磁同步电机的矢量控制
矢量控制理论由德国西门子公司的F.Blaschke于1971年提出,这是交流电机控制理论一次里程碑式的跨越。交流电机从此在直流电机高性能应用竞争中获得一隅之地,并最终形成席卷之势。矢量控制的基本思想是模仿直流电机的磁场定向方式。其原理为:以转子磁链方向作为旋转坐标系的参考方向,依据这个坐标系,将定子电流分解为与转子磁链同方向的定子电流励磁分量和与磁链方向正交的定子电流转矩分量。这两个分量相互正交,分别采用控制器控制。矢量控制可以得到精确的速度控制,良好的转矩响应,进而获得类似于直流电机的工作特性。但矢量控制需要进行较复杂的旋转坐标变换,磁链和转矩解耦控制依赖于对转子磁链的准确观测,在实际中控制效果随电机参数的变化而变化。因此矢量控制的实现需要选用较高性能的数字信号处理器、高精度的光电码盘转速传感器和适当的参数变化补偿算法。
永磁同步电机建模及控制可参考:
永磁同步电机矢量控制详细搭建过程_哔哩哔哩_bilibili
永磁同步电机建模:
https://zhuanlan.zhihu.com/p/1887559741930177528
矢量控制:FOC-控制策略
q轴电流 → 直接控制转矩(类似直流电机的电枢电流)
d轴电流 → 调节磁场:根据需要有3种情况:
- 第一种:最简单的一种,保持为零,磁链仅由转子永磁体提供,也就是id=0控制,这个时候转矩就是
- 第二种:为了在同样的电流幅值下发出更大的转矩,对dq轴电流进行合适的分配,即最大转矩电流比(MTPA)控制。
- 第三种:在所发出来的电压已经到最大值,这个时候需要弱磁控制,需要人为调整id为负。
所以:矢量控制(以转子磁场定向的控制)的核心,就是在dq同步旋转坐标系下,根据需要的转矩,控制合适的d轴和q轴电流。
https://zhuanlan.zhihu.com/p/26733002878
矢量控制:FOC-SVPWM算法合成电压矢量
https://zhuanlan.zhihu.com/p/274350505
参数的整定——如何让PI控制器实现好的性能
:https://zhuanlan.zhihu.com/p/1890415255303221563
为什么需要转速环和电流环?
:https://zhuanlan.zhihu.com/p/1889256484908557741
电流环的具体问题——解耦
:https://zhuanlan.zhihu.com/p/1892297015397954701
坐标变换
首先要提到的是两个变换,Clarck和Park变换
Clarck变换:
一般分为功率变换和幅值变换,他们不太一样
可参考:
三相交流系统中的坐标变换(abc\αβ\dq)_dq坐标系-CSDN博客
https://zhuanlan.zhihu.com/p/317347351
电机控制中Clarke变换的等幅值变换和等功率变换_等幅值变换和等功率变换的有功无功-CSDN博客
文章中包括三相坐标,abc->aB->dq等变换和逆变换,注意等幅值变换是2/3,等功率是根号2/3,
-
三相静止坐标系(abc)
-
两相静止坐标系(αβ)
-
两相旋转坐标系(dq)
Park变换:
四种Park变换:“由于国内外研究人员对abc坐标系与dq轴的定义不同,造成了Park变换矩阵的多种多样,本文则从4种定义的abc坐标系与dq轴出发,解释了4种Park矩阵的由来”
可参考文章:
https://zhuanlan.zhihu.com/p/74442400
空间矢量(SVPWM)控制
1.一般的Svpwm模块中,输入量为Vα、Vβ,得到三相计数器的Compare的值,最后输出U、V、W三相电压。在FOC控制中实现Svpwm控制的主要步骤如下:
1)、扇区判断;
2)、计算相邻两个矢量去合成想要矢量的作用时长;
3)、作用时长转换成计数器的比较值。
总体学习:https://zhuanlan.zhihu.com/p/414721065
1、扇区判断
可参考:
电机控制---SVPWM扇区判断的实现以及推导过程-CSDN博客
FOC学习笔记(六)-SVPWM扇区判断 - 侯先生的技术小站
2、矢量的作用时长
可参考:
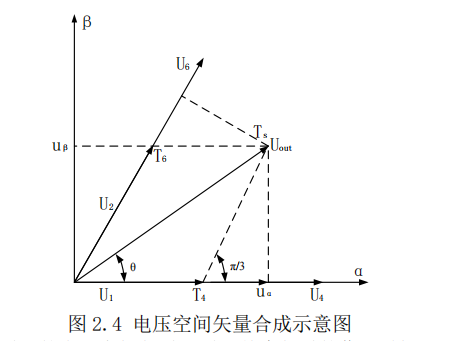
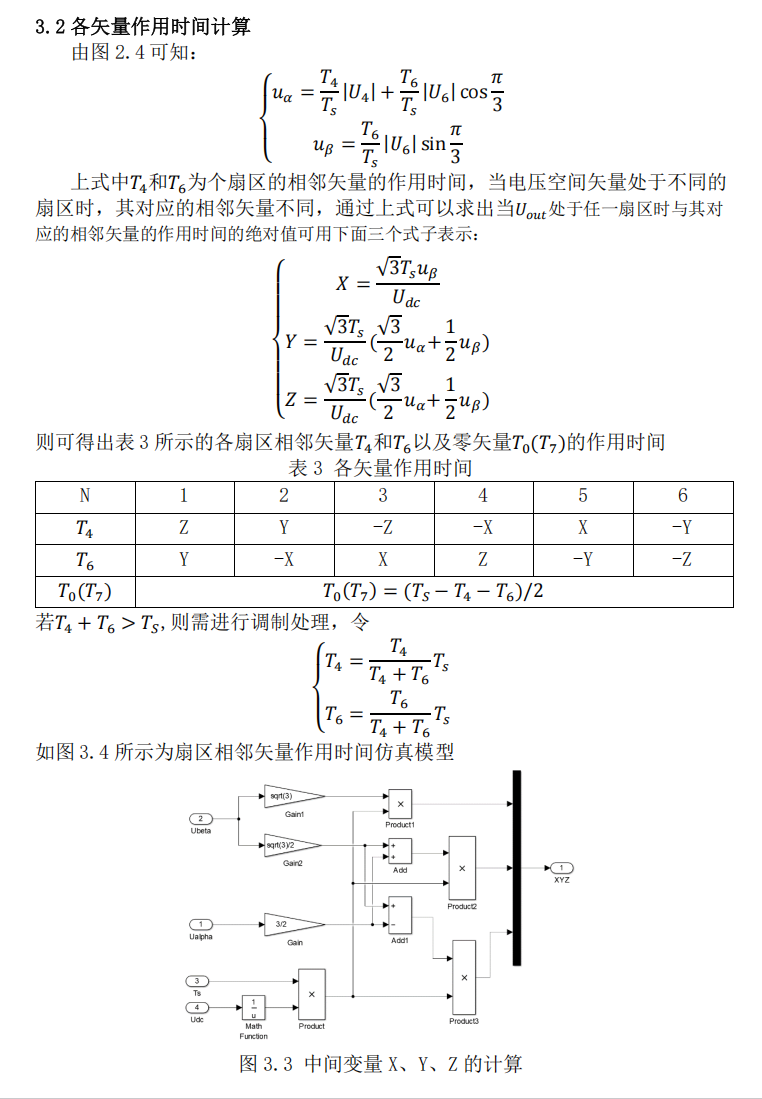
3、矢量切换点
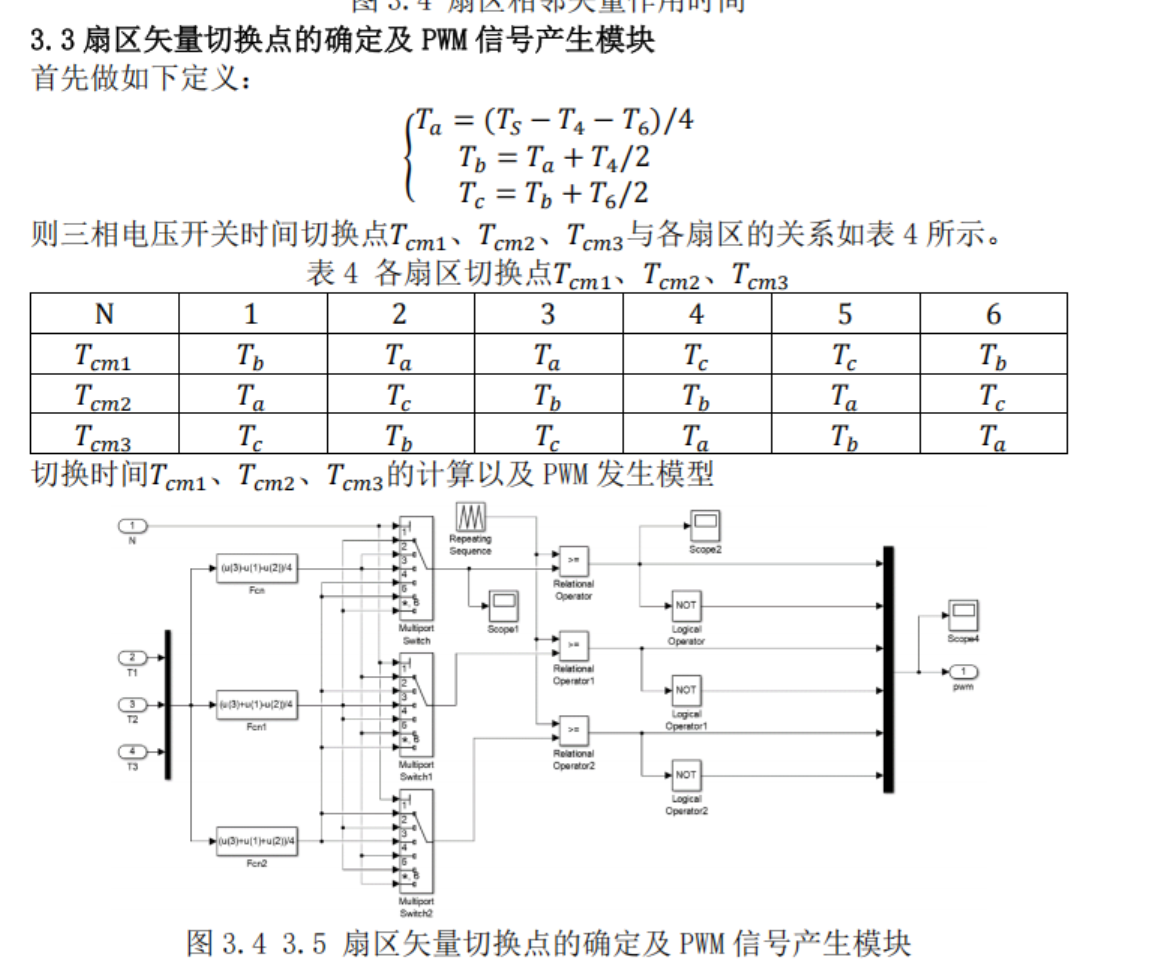
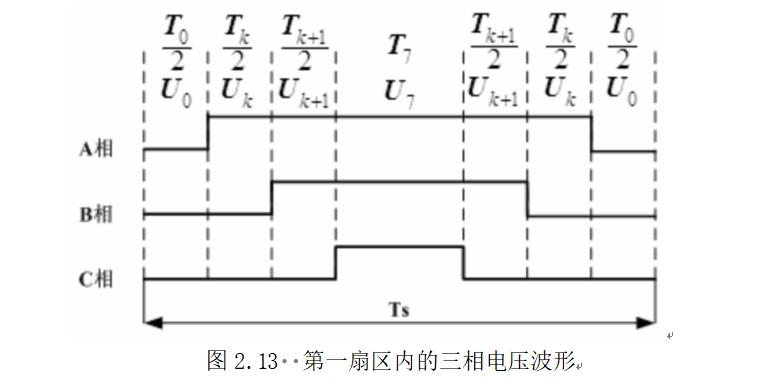
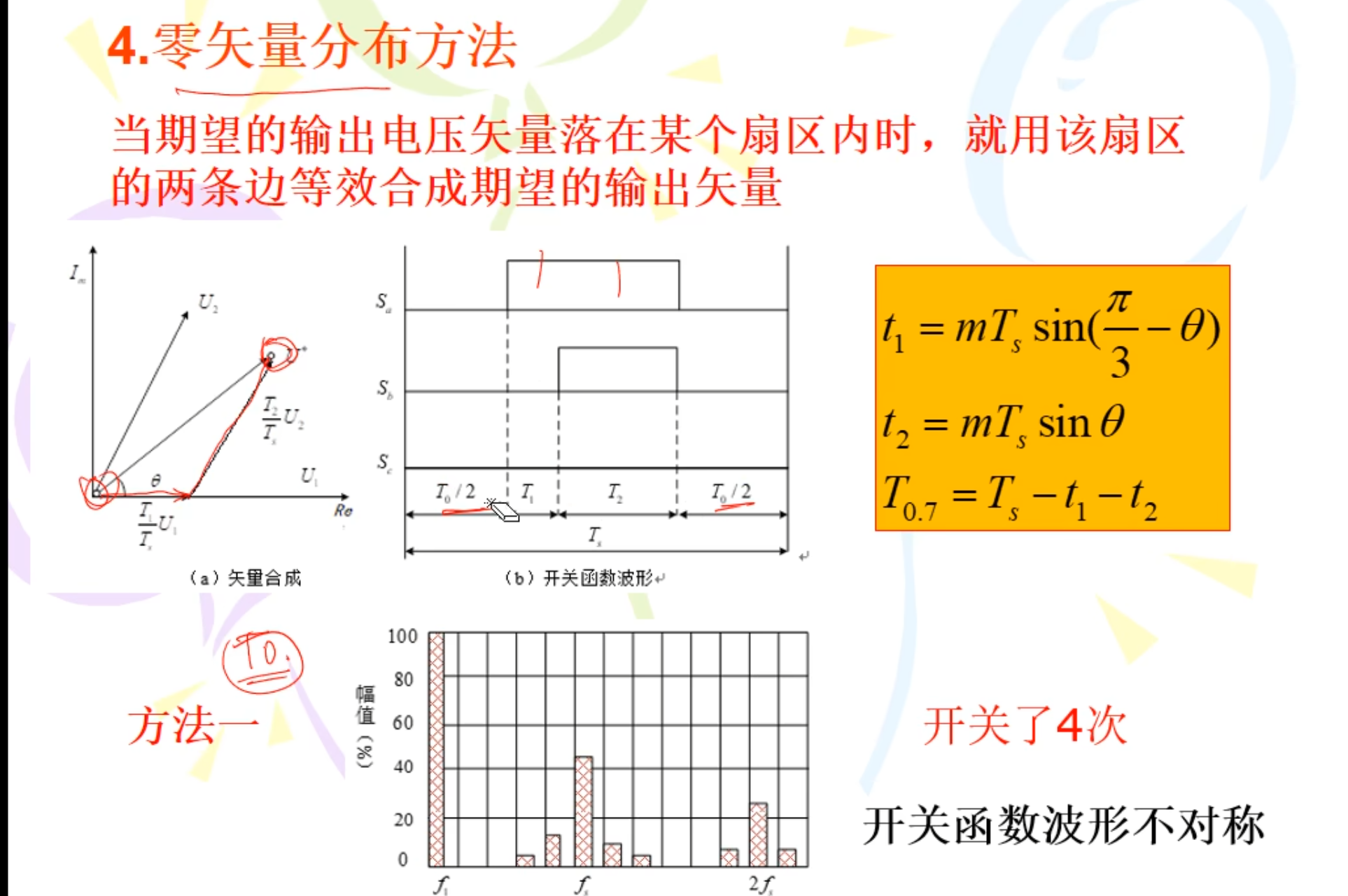
零矢量分布方法一:
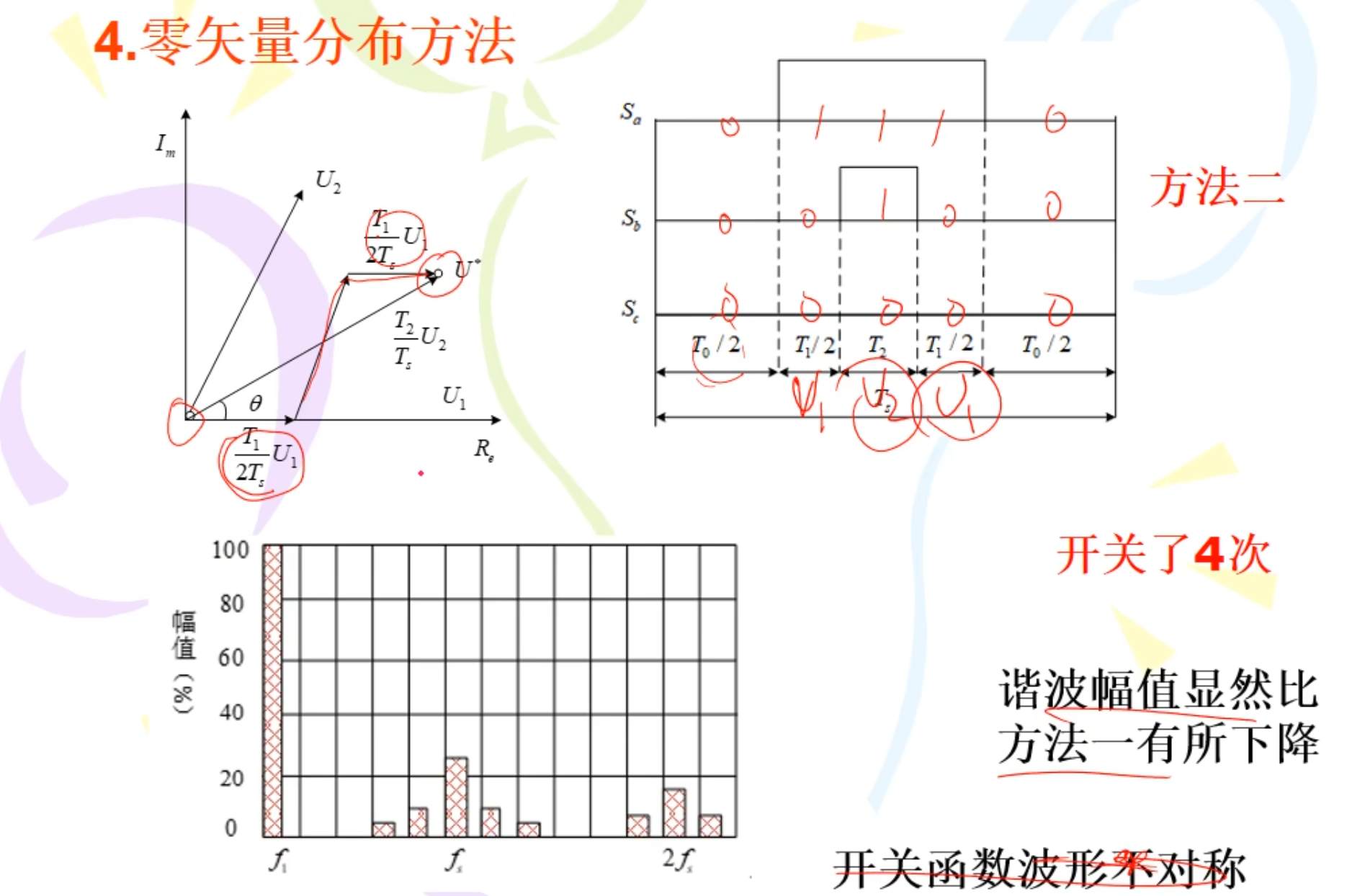
零矢量分布方法二:
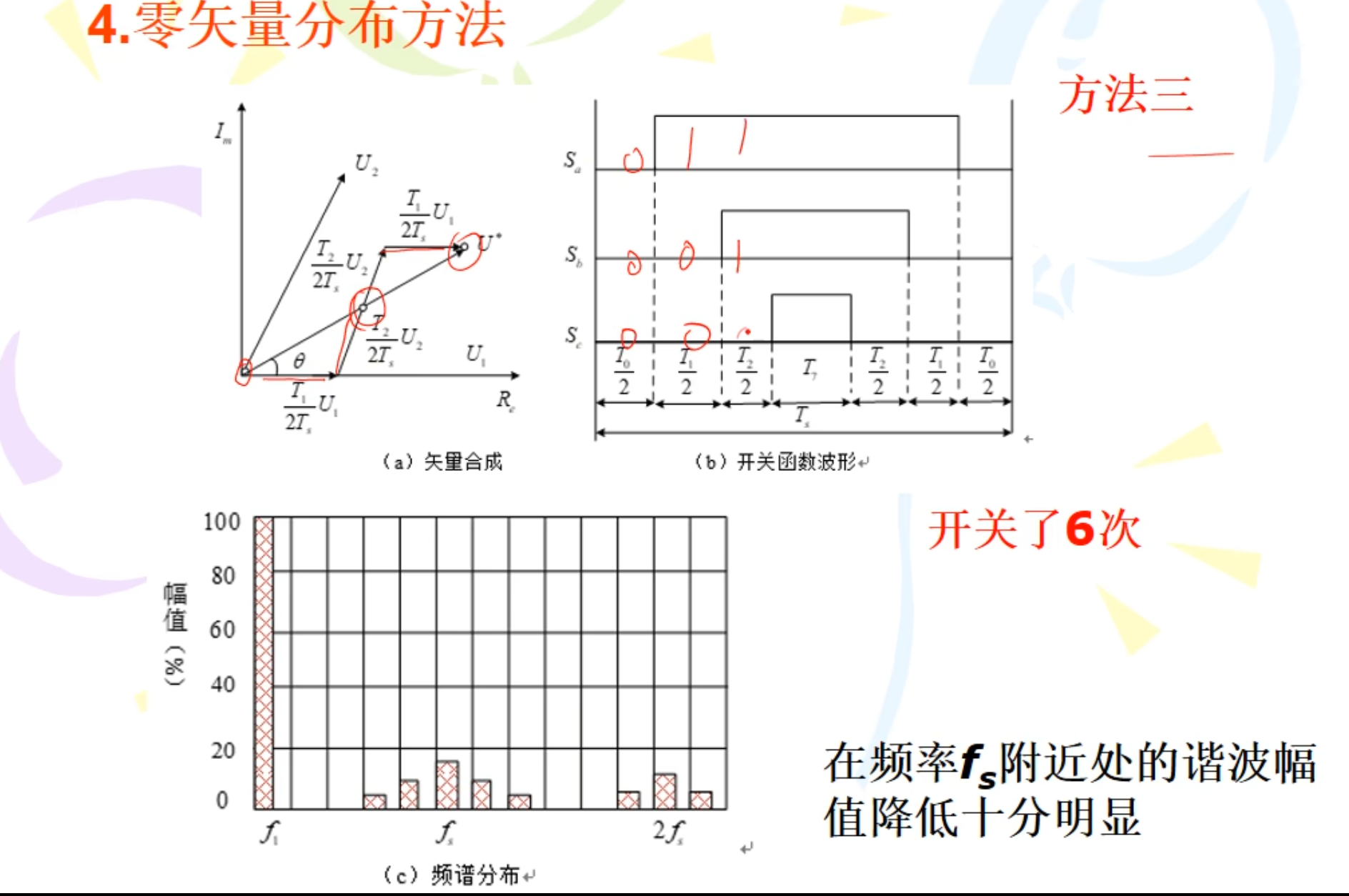
零矢量分布方法三:
总体控制框图如下:
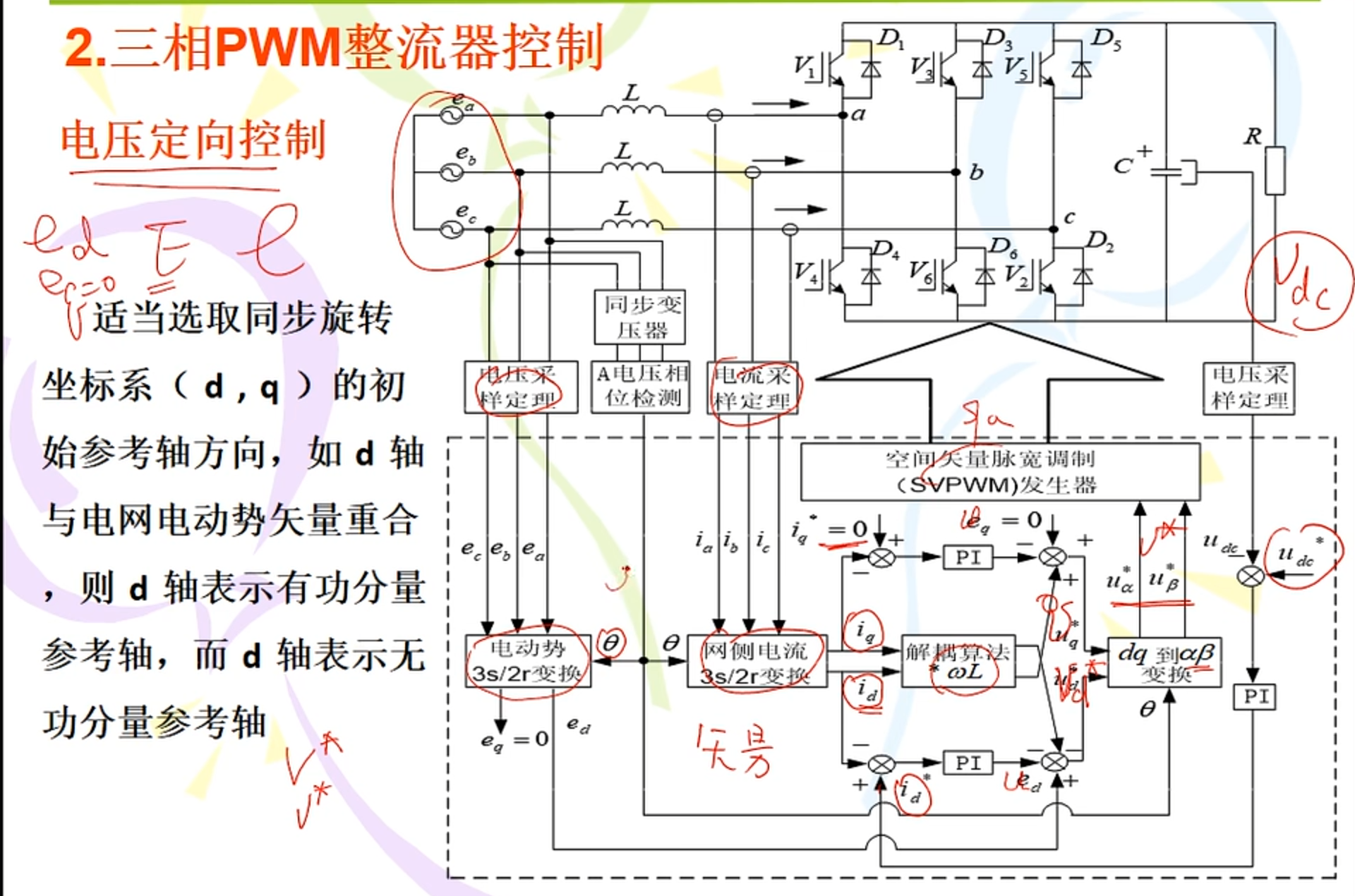
【电机控制算法】SVPWM算法的实际工程实现(基于Simulink与STM32外设场景的仿真)_stm32_丶漂泊の太阳-2048 AI社区
总结:永磁同步电机的矢量控制相比异步电机来说较为简单,由于永磁同步电机 转子为永磁体,通过安装传感器能够直接对其进行检测,而且不受电机参数的 影响,并且转子转速始终为同步转速,没有转差率,因此永磁同步电机的矢量 控制流程更为的简化,关键在于定子电流的检测,直接影响电机的控制性能。 永磁同步电机的控制方式有三种,这里采用的是 i d =0 的方式,这样可以保证用 最小的电流幅值得到最大的输出转矩,对于凸极式电机,在重负载下会导致功 率因数降低,比较适用于隐极机。另外就是最大转矩效率控制,对于凸极式同步电机充分利用其磁阻转矩,从而保证在电流幅值不变的阿情况下使得输出转矩最大。最后是采用 i d 为负值的弱磁方式,通过增加去磁电流的方法来实现弱磁升速。
磁悬浮飞轮储能系统中的永磁同步电机控制
1、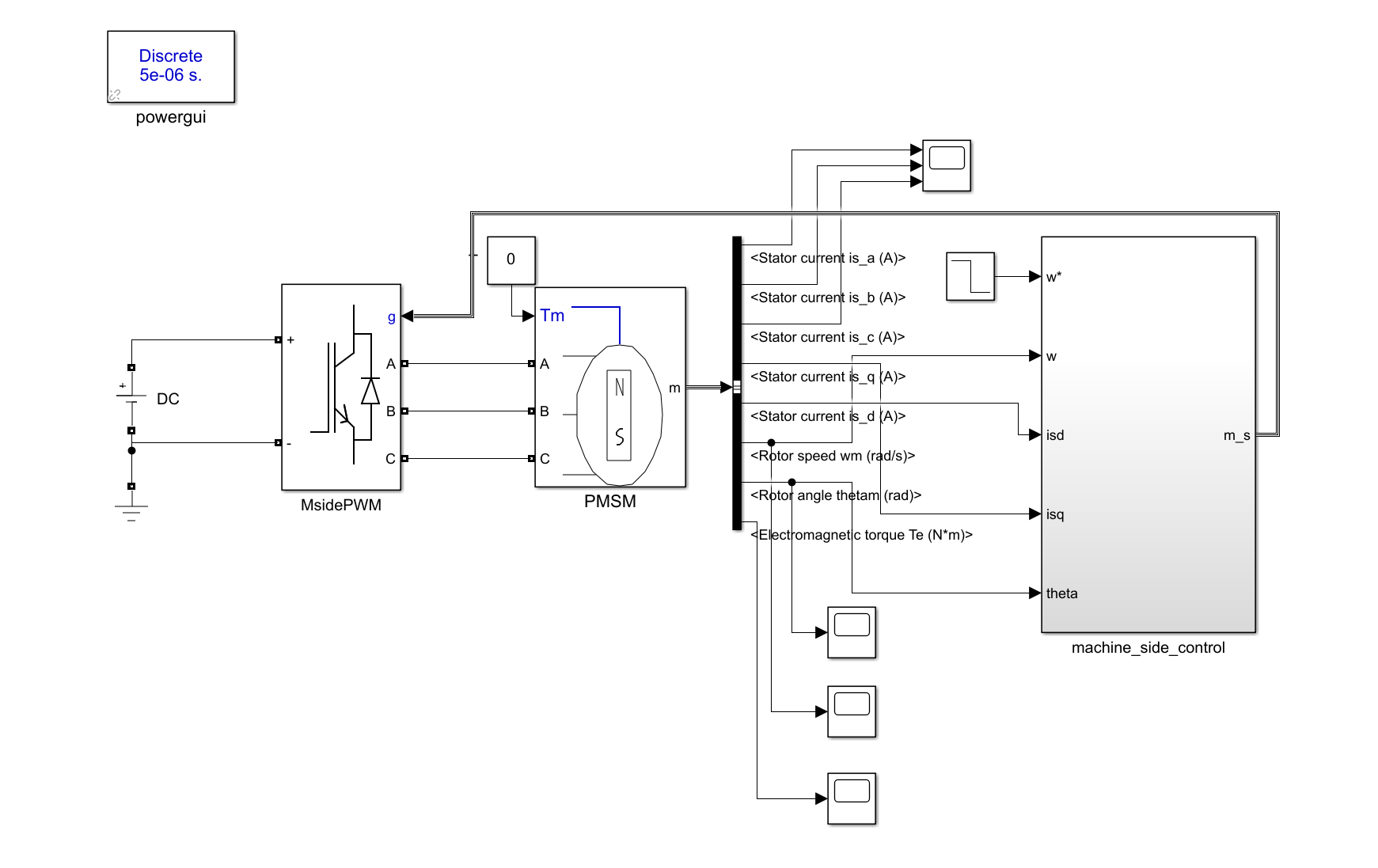
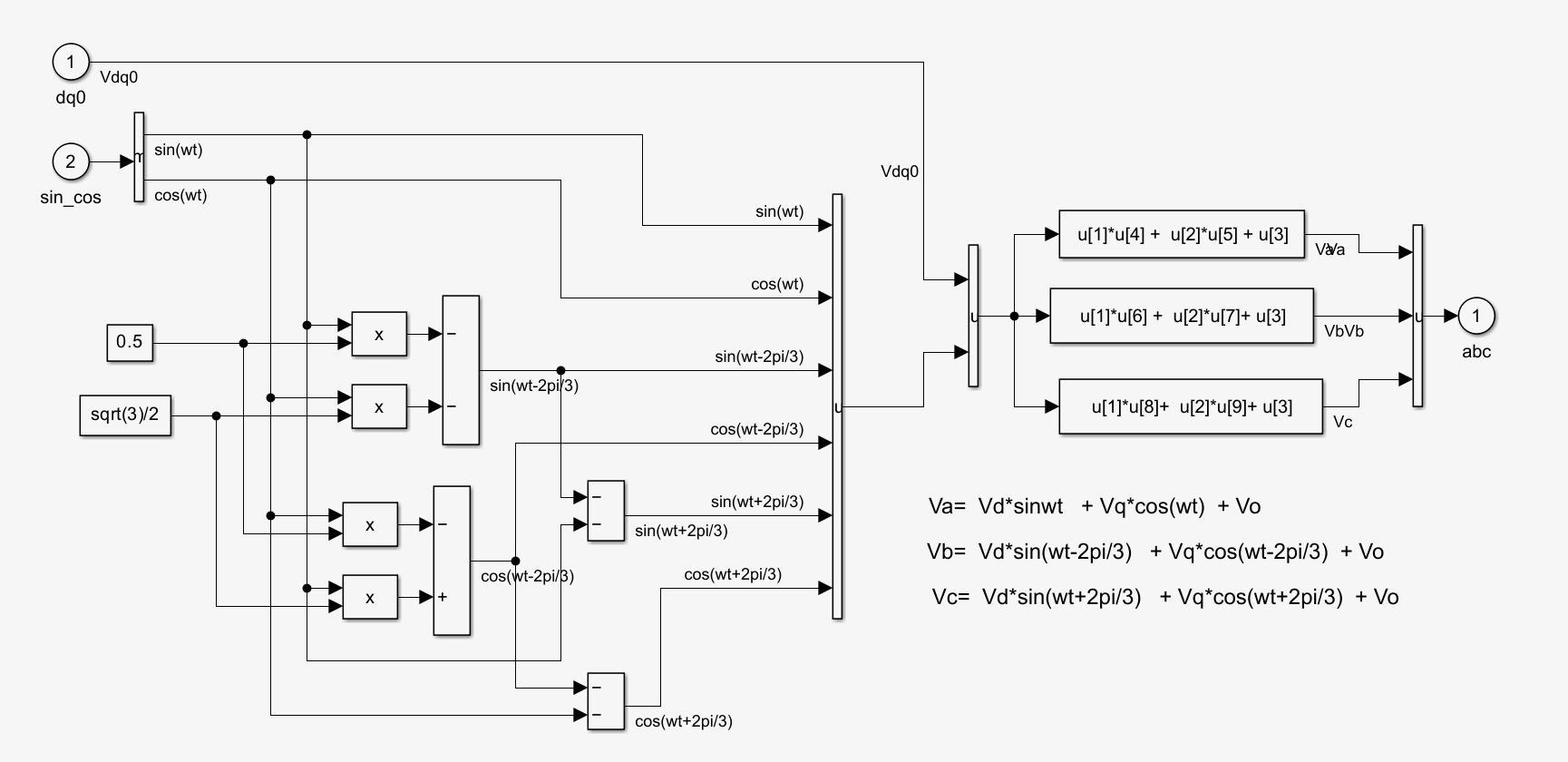
matlab的模块中提及到,对于dq->abc的变换矩阵,其根据:
When the rotating frame is aligned 90 degrees behind the phase A axis, the following relations are obtained:其公式会有不同,这个相位设置在电机模型的参数里面可以选,要对应。
-
When the rotating frame is aligned with the phase A axis at t = 0, that is, at t = 0, the d-axis is aligned with the a-axis. This type of Park transformation is also known as the cosine-based Park transformation.
-
When the rotating frame is aligned 90 degrees behind the phase A axis, that is, at t = 0, the q-axis is aligned with the a-axis. This type of Park transformation is also known as the sine-based Park transformation. Use this transformation in Simscape™ Electrical™ Specialized Power Systems models with three-phase synchronous and asynchronous machines.
这里也提到了,这里的区别是基于余弦和正弦的Park变换。

其中Udc为直流母线电压,
表2.3几种矢量控制策略的优缺点对比
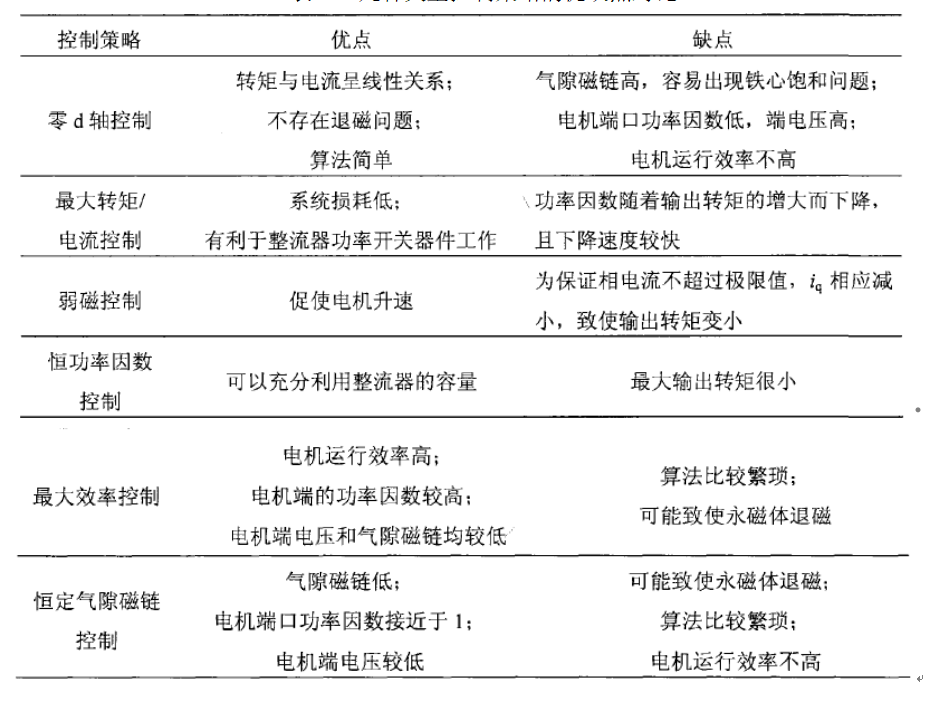
图2.14(a)和2.14(b)对比了在利用SPWM调制和利用SVPWM调制时,各自的调制波与载波的对应关系。与SPWM不同的是,SVPWM的调制波可分解为正弦基波和近似三角锯齿波两部分,如图2.14(c)所示。正是因为如此,对应于同样的中间直流电压,SVPWM满调制时输出的相电压峰值高于SPWM,也就是说,SVPWM的电压利用率比SPWM高出15%。另外,在抑制高次谐波方面的表现,SVPWM也优于SPWM,所以在大多数时候,SVPWM应用的更广泛,因此本文也采用SVPWM调制。
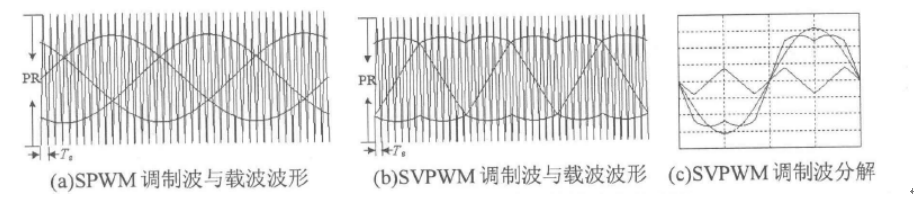
图2.14 SPWM和SVPWM的调制波于载波对应关系图
