论文解读:Mamba: Linear-Time Sequence Modeling with Selective State Spaces
题目:Mamba: Linear-Time Sequence Modeling with Selective State Spaces
时间:2024.05.31
作者:来自卡耐基梅隆的Albert Gu 和 Tri Dao
链接:https://arxiv.org/abs/2312.00752
github:https://github.com/state-spaces/mamba
摘要
作者指出,基础模型(Foundation Model)已成为深度学习研究与应用的核心驱动力,这些模型大多基于Transformer架构及其核心的注意力机制。为应对Transformer在长序列处理中的计算效率问题,研究者开发了多种次二次时间复杂度架构,包括线性注意力、门控卷积、循环模型以及状态空间模型(SSMs)。然而,这些方法在语言建模能力上仍不及注意力机制。
针对这一关键缺陷——基于内容的推理能力不足,作者团队进行了系统性改进。首先,通过将SSM参数设为输入的函数来实现稀疏建模,使模型能根据当前token动态选择性地处理序列信息。其次,尽管这种改进影响了高效卷积网络的使用,团队仍开发了一种循环模式下的硬件感知并行算法,将改进后的选择性SSM融入一个无需注意力机制、甚至比MLP更快的端到端神经网络架构。
该架构被命名为Mamba,具备显著优势:推理速度比Transformer快5倍,序列长度扩展呈线性增长,且在百万级真实序列上表现优异。作为通用序列建模框架,Mamba在多项任务中达到SOTA水平。在语言建模方面,Mamba-3B模型在预训练和下游任务中的表现不仅超越同参数规模的Transformer,甚至可与两倍参数量的Transformer媲美。
Introduction
FM和LM通常通过大规模数据训练后应用于下游任务,这类模型大多属于序列模型,能够处理可变长度的输入数据,如文本、图像和时间序列等。尽管具体实现方式存在差异,但当前主流的FM模型基本都采用了Transformer架构及其核心的注意力机制。自注意力机制使模型能够有效地捕捉密集的局部信息,从而实现对复杂数据的建模。然而,Transformer架构存在两个固有缺陷:1. 仅能处理有限长度的输入窗口,无法感知窗口外的信息;2. 计算复杂度与窗口长度呈二次方增长。作者指出,虽然已有一些改进模型试图解决这些问题,但其跨领域的有效性尚未得到充分验证。
自2021年起,SSMs作为一种新型序列建模架构展现出巨大潜力。这类模型融合了RNN和CNN的优点,既能像循环网络那样高效计算,又能保持卷积网络的特性,其模型复杂度随序列长度呈线性或近似线性增长。SSMs在Long Range Arena(如音频、图像处理)领域已取得显著成功,但在处理文本这类稀疏且信息密集的数据时仍存在局限性。
本研究团队提出了一种新型的选择性状态空间模型(SSM)框架,其核心创新点在于以下关键组件:
- Selection Mechanism 选择性机制(⭐️⭐️⭐️):团队发现现有模型存在一个关键局限——缺乏基于输入的动态数据筛选能力。针对这一痛点,受复制和感应头等合成任务的启发,团队设计了一种简洁的选择机制:
通过输入参数化SSM,使模型能够智能过滤无关信息并保留关键内容。 - Hardware-aware Algorithm 硬件感知算法:选择性机制的引入给模型计算带来了技术挑战。先前所有SSMs模型都必须保持时间和输入不变性才能保证计算效率。研究团队通过硬件感知算法成功解决了这一问题,该算法采用扫描而非卷积的循环计算方式,同时避免了状态扩展导致的不同GPU内存层级间的IO访问。最终实现的算法在理论性能和实际硬件表现上都超越了以往方法。
- Architecture 整体架构:作者团队通过将早期的SSM架构与搭配MLP的Transformer架构整合为单一模块,简化了传统的深层序列模型架构,最终形成了一种简洁的分层设计。
作为Mamba结构的扩展,选择性状态空间模型(Selective SSMs)具备全循环模型的特性,使其非常适合作为基础模型(FM)。这些关键特性包括:1. 高质量输出;2. 更快的训练和推理速度;3. 出色的长上下文处理能力。研究团队通过在合成数据、音频与基因组学以及语言建模等领域的评估,充分验证了这些优势特性。
状态空间模型(State Space Models)
S4(结构化状态空间序列模型)受到连续系统的启发,能够将一维函数或序列进行映射:
x(t)∈R→y(t)∈Rx(t) \in \mathbb{R} \rightarrow y(t)\in \mathbb{R}x(t)∈R→y(t)∈R
这一映射过程通过潜在空间h(t)∈RNh(t) \in \mathbb{R}^{N}h(t)∈RN实现。具体而言,S4模型利用四个参数(Δ,A,B,C)(\Delta,A,B,C)(Δ,A,B,C)定义了一个两阶段的序列转换过程:
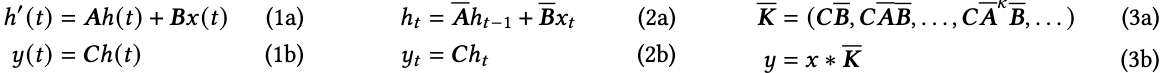
-
离散化:首先将连续参数(Δ,A,B)(\Delta,A,B)(Δ,A,B)转换为离散参数(Aˉ,Bˉ)(\bar{A},\bar{B})(Aˉ,Bˉ),转换公式为Aˉ=fA(Δ,A)\bar{A}=f_{A}(\Delta,A)Aˉ=fA(Δ,A)和Bˉ=fB(Δ,B)\bar{B} = f_{B}(\Delta,B)Bˉ=fB(Δ,B)。这对函数(fA,fB)(f_A,f_B)(fA,fB)称为离散化规则,可使用包括零阶保持器(ZOH)在内的多种规则,具体定义如下:
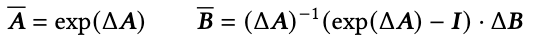
为什么要进行参数离散化操作?
原文中提到,这种离散化操作使模型具备了分辨率不变性(resolution invariance),并确保模型能够自动实现正确的归一化(properly normalized)。 -
计算:转换后的模型能否支持以下两种计算形式:线性递归(linear recurrence)和全局卷积(global convolution)。通常,前者在自回归推理中更具优势,而后者则能实现更高效的并行训练。
-
线性时间不变性(LTI):图1所示转换过程的核心特性是模型动态在时间维度上保持恒定。具体而言,参数(Δ,A,B,C)(\Delta,A,B,C)(Δ,A,B,C)和(Aˉ,Bˉ)(\bar{A},\bar{B})(Aˉ,Bˉ)在所有时间步都保持不变,这一特性被称为线性时间不变性(linear time invariance)。基于此,作者团队认为LTI SSMs与任何线性递归或卷积在形式上是等价的。
-
SSM概览:实际上,SSMs并非特指单一模型,而是结构化SSMs(structured SSMs)和S4模型等系列模型的总称,包括强化学习中的马尔可夫决策过程和控制系统中的卡尔曼滤波等。
-
SSM架构:作为一个独立的序列转换模块,SSMs可以无缝集成到端到端的神经网络框架中。研究还探讨了若干著名SSM架构,这些架构将作为主要baseline进行比较。
选择性状态空间模型(Selective State Space Models)
Part1——动机(⭐️⭐️⭐️):选择作为一种压缩的手段(Selection as a a Means of Compression) 这个部分非常重要用于阐述作者原始动机,而且原文的该部分描述得相当好
研究团队首先指出,这种动机源于合成任务的需求。基于此,他们提出序列建模的核心在于将上下文信息压缩到更小的状态空间。从这个角度出发,可以重新审视主流序列模型的取舍:例如注意力机制之所以有效或失效,本质在于其完全不压缩上下文信息。这种特性导致自回归推理需要精确存储整个上下文(如KV缓存机制),从而引发线性时间的推理延迟和平方级的训练耗时。相比之下,循环模型之所以高效,正是因其具备有限状态空间,实现了固定时间的推理和线性时间的训练。当然,其效果优劣取决于该状态空间对上下文的压缩能力。
为了理解这个原则原文给出了两个运行合成任务的案例。如下图所示:
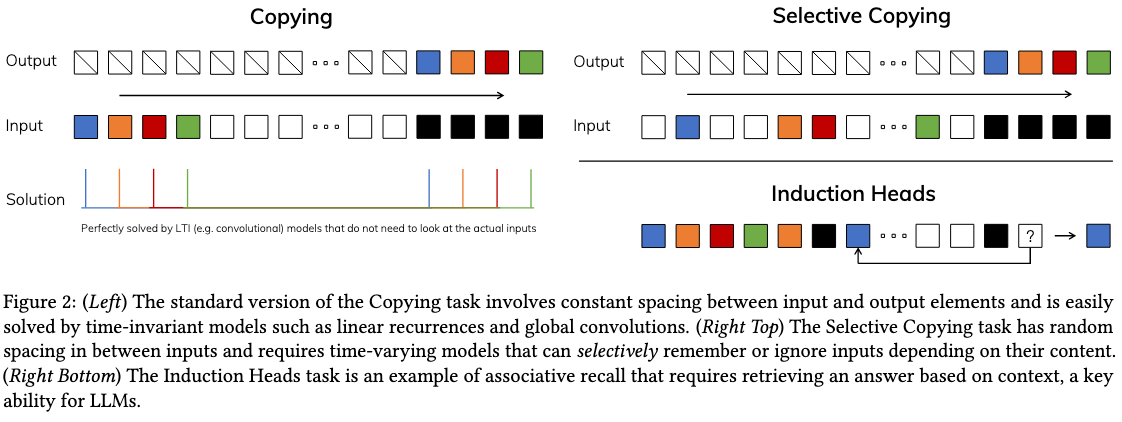
- 左图(Copying 机制):该模块对经典复制任务进行了选择性改进,通过动态调整 token 位置来实现记忆功能。这要求下文感知归因机制能够有效识别并保留相关 token,同时过滤无关信息。
- 右图(Induction Head 机制):该理论假设解释了大型语言模型获取核心上下文能力的内在机制,其运作依赖于上下文感知归因系统,确保模型能在恰当的语境中生成准确输出。
研究揭示了LTI模型的固有缺陷。从循环模型的角度分析,其固定的动态特性使其难以从上下文中选择正确信息,也无法以输入独立的方式在序列传递过程中有效影响隐藏状态;而就卷积网络而言,虽然全局卷积能较好地处理原始复制任务(因其仅需时间感知能力),但在选择任务上表现欠佳,这源于其缺乏上下文感知能力。具体而言,当输入输出空间存在变化时,静态卷积核难以进行有效建模。
研究表明,模型效率与有效性之间的权衡本质上取决于状态压缩能力:高效模型需要维持较小的状态规模,而有效模型则要求状态能充分包含上下文信息。基于此,研究团队提出一个核心原则:构建具有选择性的序列模型,使上下文处理能力能够聚焦或过滤输入信息。具体来说,这种选择机制控制着信息如何在序列维度上流动和交互。 ⭐️⭐️⭐️
这一部分突出了Selective机制在序列建模中的核心作用,它直接影响着模型的效率和性能表现。后续研究应当重点关注如何针对Selective机制进行权衡取舍。
