优选算法 力扣 11. 盛最多水的容器 双指针降低时间复杂度 贪心策略 C++题解 每日一题

零、题目描述

题目链接：盛最多水的容器

题目描述：

示例 1：

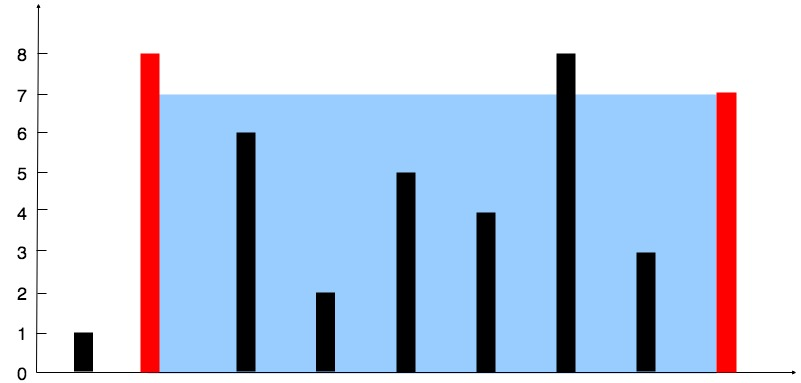
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：
输入：height = [1,1]
输出：1

提示：
n == height.length
2 <= n <= 10^5
0 <= height[i] <= 10^4

一、为什么这道题值得你花几分钟看懂？

盛最多水的容器问题，是双指针算法中“贪心策略”的经典体现。它的价值在于：让你明白如何通过“主动放弃不可能的选项”来优化时间复杂度。

这道题看似需要枚举所有可能的两条线组合（暴力解法的思路），但通过观察容器容量的计算逻辑，我们能发现一个关键规律：容量由“短板”和“间距”共同决定。这个规律让双指针的“收缩法”有了用武之地——通过巧妙移动左右指针，我们能在 O(n) 时间内找到最优解，而不是暴力法的 O(n²)。

搞定这道题，你会掌握：

• 如何从问题本质中提炼贪心策略的依据
• 双指针在“范围搜索”类问题中的应用技巧
• 如何用数学逻辑证明算法的正确性

这种“抓住核心矛盾，主动排除无效解”的思维，对解决数组、字符串类的优化问题至关重要。

二、从暴力枚举到双指针：思路的进化

1. 暴力枚举：直观但低效的尝试

这是我最开始接触这道题的想法也是最容易想到的思路是：枚举所有可能的左右边界组合，计算每个组合的容量，取最大值。

暴力解法代码：

class Solution {
public:int maxArea(vector<int>& height) {int max = -1;// 枚举右边界for(int right = height.size() - 1; right >= 0; right--){// 枚举左边界（左边界 <= 右边界）for(int left = 0; left <= right; left++){// 容量 = 水平距离 * 短板高度int capacity = abs(left - right) * min(height[left], height[right]);max = std::max(max, capacity);}}return max;}
};

问题分析：

• 时间复杂度：O(n²)，当 n 为 10^5 时，运算次数高达 10^10，必然超时
• 空间复杂度：O(1)，只使用常数个变量
• 核心缺陷：存在大量重复计算和无效比较，比如当左右边界间距减小时，若短板高度没有显著增加，容量一定更小

2. 双指针：用贪心策略减少无效计算

观察容量公式 capacity = (right - left) * min(h[left], h[right]) 可知：

• 容量由两个因素决定：左右指针的间距（right - left）和两块板中的短板（min值）
• 当间距减小时，只有短板高度增大，才有可能让容量变大

双指针思路：

• 初始时，左右指针分别指向数组两端（left=0，right=n-1），此时间距最大
• 计算当前容量，更新最大值
• 移动短板对应的指针（若 h[left] < h[right]，则 left++；否则 right–）
• 重复上述步骤，直到 left >= right

为什么移动短板？

• 若移动长板：新的短板要么不变（还是原来的短板），要么变小（新的板更短），而间距一定减小，容量必然变小
• 若移动短板：可能出现新的短板比原来长，即使间距减小，容量仍有可能增大

这种策略本质是：每次放弃不可能成为最优解的选项，保留潜在更优的可能性。

三、双指针实现：贪心策略的应用

1. 算法步骤

1. 初始化左右指针 left = 0，right = height.size() - 1，最大容量 max = 0
2. 当 left < right 时，循环：
   • 计算当前容量 capacity = (right - left) * min(h[left], h[right])
   • 若当前容量大于 max，更新 max
   • 移动短板指针：若 h[left] <= h[right] 则 left++，否则 right--
3. 循环结束后，返回 max

2. 代码实现

class Solution {
public:int maxArea(vector<int>& height) {int max = -1;int left = 0;                  // 左指针初始在最左端int right = height.size() - 1; // 右指针初始在最右端while(left < right){// 计算当前左右指针形成的容量int capacity = (right - left) * min(height[left], height[right]);// 更新最大容量max = std::max(max, capacity);// 移动短板指针if(height[left] > height[right])right--;  // 右板是短板，左移右指针elseleft++;   // 左板是短板，右移左指针}return max;}
};

四、代码解析与复杂度分析

代码走读（示例1：height = [1,8,6,2,5,4,8,3,7]）

1. 初始状态：left=0，right=8（值为7），容量 = 8 * min(1,7) = 8 → max=8
2. 左板是短板（1 < 7），left++ → left=1（值为8）
3. 当前容量 = 7 * min(8,7) = 49 → max=49
4. 右板是短板（7 < 8），right-- → right=7（值为3）
5. 当前容量 = 6 * min(8,3) = 18 → max保持49
6. 右板是短板（3 < 8），right-- → right=6（值为8）
7. 当前容量 = 5 * min(8,8) = 40 → max保持49
8. 两板等高，移动任一指针（此处left++）→ left=2（值为6）
9. 后续步骤继续移动短板指针，均未出现更大容量，最终返回49

复杂度分析

复杂度类型	具体值	说明
时间复杂度	O(n)	左右指针从两端向中间移动，每个元素最多被访问一次
空间复杂度	O(1)	只使用常数个额外变量，与输入规模无关

五、常见问题与证明

1. 为什么双指针不会错过最优解？

假设最优解由 (i,j) 构成（i < j），当指针移动到 (i,k) 且 k > j 时：

• 若此时 h[i] 是短板，会移动 i 直到 i 到达最优左边界
• 若此时 h[k] 是短板，会移动 k 直到 k 到达最优右边界

反证法：若最优解被错过，则说明在到达 (i,j) 前，其中一个指针被提前移动。但根据移动规则，只有当存在更短的板时才会移动，这与 (i,j) 是最优解矛盾，因此不会错过。

2. 两板等高时移动哪一个？

当 h[left] == h[right] 时，移动任一指针均可：

• 因为无论移动哪一个，下一次的间距都会减小，而新的短板不会超过当前高度，容量一定更小
• 后续步骤仍会覆盖所有可能的组合

3. 为什么初始指针要放在两端？

初始间距最大，此时的容量是所有组合中“间距最大”的候选解。若初始指针在中间，会错过更大间距的可能组合。

六、举一反三

这道题的双指针+贪心思路可推广到：

• 范围优化问题：如寻找数组中满足某种条件的最大/最小区间
• 两个变量决定结果的问题：当结果由两个变量共同决定，且存在单调性时，可通过移动指针优化

下一题预告：LeetCode 611. 有效三角形的个数！这道题会让你看到双指针在“三重循环优化”中的妙用——如何将 O(n³) 的暴力解法，通过排序+双指针降维到 O(n²)。三角形的成立条件暗藏着指针移动的规律，明天的解析会带你拆解其中的逻辑，让你再次感叹双指针的强大！

最后欢迎大家在评论区分享你的代码或思路，咱们一起交流探讨~ 🌟 要是有大佬有更精妙的思路或想法，恳请在评论区多多指点批评，我一定会虚心学习，并且第一时间回复交流哒！

这是封面原图呀～ 既然能追到这里，想必你也是对算法爱得深沉、和这篇博客同频共振的“同道之猿”吧～

✨ 如果你觉得这些思路对你有启发，不妨动动手指：

• 🌟 点个赞，让这份思考被更多人看见
• ⭐ 收个藏，下次遇到类似问题能快速找回灵感
• 👀 加个关注，后续更新的解题干货绝对不会让你迷路

毕竟，在算法的世界里，互相照亮的每一步，都走得更有力量呀～ 咱们下篇题解再见！😉