当前位置：首页 > news >正文

嵌入式 - 数据结构：查找至双向链表

news 2025/8/5 8:17:41

一、链表的查找：精准定位数据

1. 基本实现逻辑

2. 代码实现

3. 补充知识点

二、链表的修改：高效更新数据

1. 实现逻辑

2. 代码实现

3. 补充知识点

三、链表的尾插：在末端添加元素

1. 实现步骤

2. 代码实现

3. 补充知识点

四、链表的销毁：释放内存资源

1. 实现逻辑

2. 代码实现

1. C语言的按值传递机制

3. 补充知识点

五、链表的特殊查找：中间节点与倒数第 k 个节点

1. 查找中间节点

2. 查找倒数第 k 个节点

六、特殊场景下的删除：无表头时删除中间节点

1. 实现思路

2. 代码实现

3. 补充知识点

七、链表的倒置：反转数据顺序

1. 实现思路（头插法）

2. 代码实现

3. 补充知识点

八、链表的排序：冒泡与选择排序

1. 冒泡排序

2. 选择排序

3. 补充知识点

九、链表的环问题：判断、环长与入口

1. 判断链表是否有环

2. 计算环长

3. 查找环的入口

4. 综合代码实现

十、双向链表：更灵活的双向访问

1. 节点定义

2. 双向链表的基本操作

1. 创建空双向链表

2. 头插法插入节点

3. 遍历链表

4. 查找节点

5. 修改节点数据

6. 删除节点

7. 销毁链表

十一、双向链表的优缺点

优点

缺点

在数据结构的世界里，链表以其灵活的内存管理和高效的插入删除操作，成为了程序员必备的基础知识。本文将从链表的查找操作开始，深入剖析链表的各类高级操作、双向链表的实现以及工程管理工具 Makefile 的使用，为你呈现一套完整的链表学习体系。

一、链表的查找：精准定位数据

链表的查找操作是数据访问的基础，其核心思想是通过遍历链表逐一比对节点数据，找到目标元素后返回节点地址。

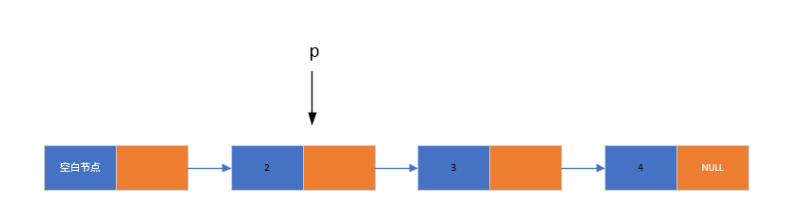
1. 基本实现逻辑

从链表的第一个有效节点开始遍历（头节点的下一个节点）
每次访问一个节点时，判断其数据是否与目标值匹配
若匹配，立即返回该节点的地址；若遍历至链表末尾仍未找到，返回 NULL

2. 代码实现

/* 找到符合要求的第一个元素节点地址 */
linknode *find_linklist(linknode *phead, datatype tmpdata) {linknode *ptmpnode = NULL;ptmpnode = phead->pnext;while (ptmpnode != NULL) {if (ptmpnode->data == tmpdata) {return ptmpnode;}ptmpnode = ptmpnode->pnext;}return NULL;
}

3. 补充知识点

时间复杂度：O (n)，其中 n 为链表长度。在最坏情况下，需要遍历整个链表才能确定目标元素是否存在。
优化思路：对于频繁查找的场景，可以结合哈希表记录节点地址，将查找时间复杂度降至 O (1)，但会增加空间开销。
应用场景：在链表中查找指定元素、判断元素是否存在、获取元素位置等基础操作中均有应用。

二、链表的修改：高效更新数据

链表的修改操作基于查找操作，找到目标元素后直接更新其数据域的值，操作简单但需注意边界情况。

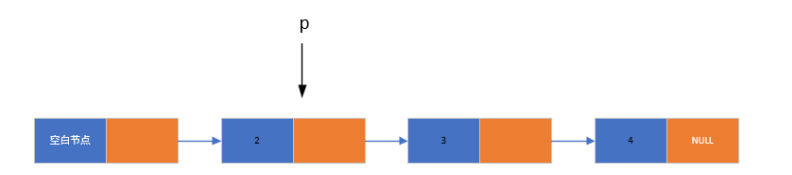
1. 实现逻辑

沿用遍历思想，遍历链表找到所有符合条件的旧值节点
将找到的节点数据更新为新值
继续遍历至链表末尾，确保所有匹配节点都被修改

2. 代码实现

/* 将符合条件的旧值修改为新值 */
int update_linklist(linknode *phead, datatype olddata, datatype newdata) {linknode *ptmpnode = NULL;ptmpnode = phead->pnext;while (ptmpnode != NULL) {if (ptmpnode->data == olddata) {ptmpnode->data = newdata;}ptmpnode = ptmpnode->pnext;}return 0;
}

3. 补充知识点

操作特性：修改操作仅改变节点的数据域，指针关系不受影响，因此时间复杂度与查找一致，为 O (n)。
注意事项：
- 若链表中存在多个相同的旧值，上述代码会全部修改，若需仅修改第一个匹配节点，找到后可直接退出循环。
- 在多线程环境下，修改操作需加锁保护，避免数据不一致问题。
扩展应用：可用于实现链表的批量更新、条件替换等功能，例如将链表中所有小于 0 的数改为 0。

三、链表的尾插：在末端添加元素

尾插法是链表插入操作的一种重要方式，与头插法不同，它将新元素添加到链表的末尾，保证元素的插入顺序与逻辑顺序一致。

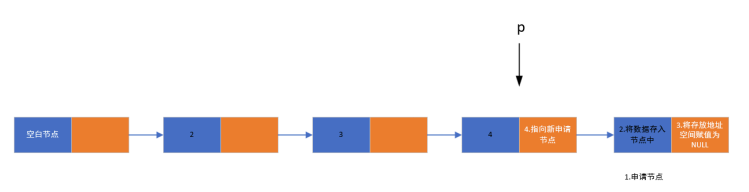
1. 实现步骤

申请新的节点空间，并为其数据域赋值
将新节点的指针域设为 NULL（表示它将成为新的尾节点）
遍历链表找到当前的最后一个节点
将最后一个节点的指针域指向新节点，完成插入

2. 代码实现

/* 尾插法插入节点元素 */
int insert_tail_linklist(linknode *phead, datatype tmpdata) {linknode *ptmpnode = NULL;linknode *plastnode = NULL;// 申请节点ptmpnode = malloc(sizeof(linknode));if (NULL == ptmpnode) {perror("fail to malloc");return -1;}// 为新节点赋值ptmpnode->data = tmpdata;ptmpnode->pnext = NULL;// 找到最后一个节点plastnode = phead;while (plastnode->pnext != NULL) {plastnode = plastnode->pnext;}// 插入新节点plastnode->pnext = ptmpnode;return 0;
}

3. 补充知识点

效率优化：上述实现的时间复杂度为 O (n)，因为每次插入都需要遍历找尾节点。若在链表结构中增加一个尾指针（专门记录最后一个节点的地址），可将尾插法的时间复杂度优化至 O (1)，这也是队列（FIFO）数据结构常用的实现方式。
与头插法对比：
- 头插法插入效率高（O (1)），但插入的元素顺序与输入顺序相反。
- 尾插法插入顺序与输入顺序一致，但未优化时效率较低。
应用场景：日志记录、消息队列等需要保持数据插入顺序的场景，通常采用尾插法实现。

四、链表的销毁：释放内存资源

链表使用动态内存分配，若不及时销毁会导致内存泄漏，因此销毁操作是链表生命周期管理的重要环节。

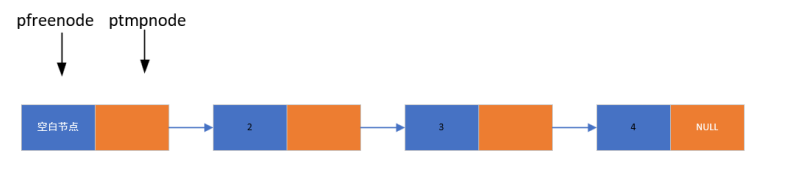
1. 实现逻辑

定义两个指针，分别用于遍历（ptmpnode）和释放（pfreenode）节点
从头部开始，先记录下一个节点的地址，再释放当前节点
循环执行，直至所有节点都被释放
最后将头指针置为 NULL，避免野指针

2. 代码实现

/*销毁链表*/
int destory_linklist(linknode **pphead)
{linknode *ptmpnode = NULL;linknode *pfreenode = NULL;ptmpnode = *pphead;pfreenode = *pphead;while(ptmpnode != NULL){ptmpnode = ptmpnode->pnext;//后一个指针指向下一个节点free(pfreenode);//释放前一个节点pfreenode = ptmpnode;//前一个节点指针往后走}*pphead = NULL; //在里面置空return 0;
}

while (pfast != NULL)
{
pfast = pfast->pnext;//快指针走一步
if(pfast == NULL)
{
break;
}
// pslow = pslow->pnext;
//可以选择删中间的前一个节点还是后一个节点
pfast = pfast->pnext;//快指针走两部两步
if(pfast == NULL)
{
break;
}
pslow = pslow->pnext;//慢指针走一步
}

1. C语言的按值传递机制

C语言中，函数参数传递是按值传递（pass by value）。这意味着当我们将一个指针（如链表头指针 Node* head）传递给函数时，函数内部接收到的是该指针的副本，而不是原始指针本身。
因此，在销毁函数中：
- 如果只传递单指针（Node* head），函数可以释放链表节点占用的内存（因为指针副本指向相同的内存地址）。
- 但函数无法修改原始头指针的值（例如将其设置为 NULL），因为修改的只是副本。
- 这会导致一个问题：销毁后，原始头指针可能仍然指向已释放的内存区域（称为悬空指针），后续访问可能引发崩溃或未定义行为。

对此有类似解释：在链表初始化函数中，使用二级指针（双指针）是为了改变主函数中头指针指向的地址，确保修改能反映到原始指针上

3. 补充知识点

内存管理重要性：在长期运行的程序（如服务器）中，链表若不销毁会持续占用内存，最终可能导致程序崩溃。因此，链表使用完毕后必须调用销毁函数。
递归销毁的风险：除了迭代销毁，也可通过递归实现销毁，但对于长链表，递归会导致栈溢出，因此迭代方式更安全。
野指针预防：销毁后将头指针置为 NULL 是关键，否则头指针会成为野指针（指向已释放的内存），再次使用可能引发程序异常。

五、链表的特殊查找：中间节点与倒数第 k 个节点

链表的特殊查找问题是算法面试的高频考点，主要包括查找中间节点和倒数第 k 个节点，这类问题可通过快慢指针技巧高效解决。

1. 查找中间节点

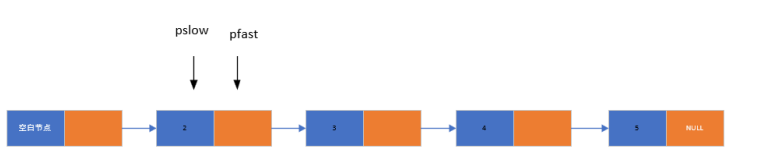
核心思想：定义快、慢两个指针，快指针每次走 2 步，慢指针每次走 1 步。当快指针到达链表末尾时，慢指针恰好指向中间节点。
代码实现：

/* 查找链表中间节点 */
linknode *find_midnode(linknode *phead) {linknode *pslow = NULL;linknode *pfast = NULL;pslow = pfast = phead->pnext;while (pfast != NULL) {pfast = pfast->pnext;if (NULL == pfast) {break;}pfast = pfast->pnext;if (NULL == pfast) {break;}pslow = pslow->pnext;}return pslow;
}

应用场景：链表的归并排序（需将链表从中间分割为两部分）、判断链表是否为回文（对比中间节点两侧的元素）等。

2. 查找倒数第 k 个节点

核心思想：快指针先向前走 k 步，然后快慢指针同时以步长 1 前进。当快指针到达末尾时，慢指针所在位置即为倒数第 k 个节点。
代码实现：

/* 查找链表倒数第k个节点 */
linknode *find_last_kth_node(linknode *phead, int k) {int i = 0;linknode *pfast = NULL;linknode *pslow = NULL;pfast = phead->pnext;// 快指针先走k步for (i = 0; i < k && pfast != NULL; i++) {pfast = pfast->pnext;}// 若快指针提前为空，说明k大于链表长度if (NULL == pfast) {return NULL;}// 快慢指针同时前进pslow = phead->pnext;while (pfast != NULL) {pfast = pfast->pnext;pslow = pslow->pnext;}return pslow;
}

边界处理：需考虑 k 为 0、k 大于链表长度等异常情况，避免程序崩溃。实际应用中可先判断 k 的合法性（k>0），并通过遍历获取链表长度后再执行查找。

六、特殊场景下的删除：无表头时删除中间节点

在某些场景下，我们可能无法获取链表的头节点，此时删除指定中间节点需要采用特殊技巧。

1. 实现思路

无法通过前驱节点修改指针关系，因此采用 “数据覆盖法”：将当前节点的下一个节点的数据复制到当前节点，然后删除下一个节点。
本质是通过删除下一个节点来 “间接删除” 当前节点，避免了寻找前驱节点的过程。

2. 代码实现

/* 删除指定节点（无表头时） */
int delete_linknode(linknode *ptmpnode) {linknode *pnextnode = NULL;pnextnode = ptmpnode->pnext;// 复制下一个节点的数据ptmpnode->data = pnextnode->data;// 修改指针关系，跳过下一个节点ptmpnode->pnext = pnextnode->pnext;// 释放下一个节点free(pnextnode);
pnextnode = NULL;//最好也像销毁一样置成空//但其实是局部变量的话不影响return 0;
}

pnextnode = NULL;//最好也像销毁一样置成空
//但其实是局部变量的话不影响

3. 补充知识点

局限性：该方法无法删除链表的最后一个节点（因为最后一个节点没有下一个节点），因此使用前需确保目标节点不是尾节点。
适用场景：当只能获取中间节点的地址，且无法访问头节点时（如某些链表封装的 API 仅暴露节点指针），可采用此方法。
设计思想：通过数据复制规避指针修改的限制，体现了 “曲线救国” 的问题解决思路。

七、链表的倒置：反转数据顺序

链表的倒置（反转）是将链表中元素的顺序完全颠倒，例如将 1→2→3→NULL 变为 3→2→1→NULL，是链表操作中的经典问题。

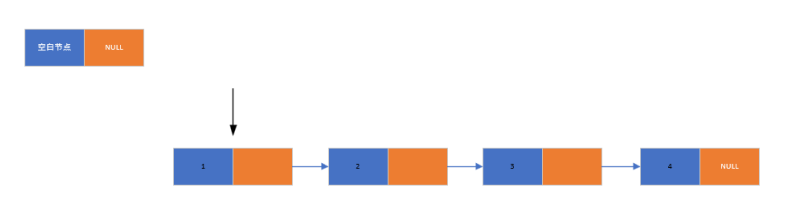
1. 实现思路（头插法）

将原链表从头部断开，使头节点的指针域指向 NULL
遍历原链表的每个节点，依次采用头插法插入到新链表中
头插法的特性会自动实现元素顺序的反转

2. 代码实现

/* 链表倒置 */
int reverse_linklist(linknode *phead) {linknode *pinsertnode = NULL;linknode *ptmpnode = NULL;// 将链表从头结点处断开ptmpnode = phead->pnext;phead->pnext = NULL;// 依次将所有元素使用头插法插入while (ptmpnode != NULL) {pinsertnode = ptmpnode;ptmpnode = ptmpnode->pnext;pinsertnode->pnext = phe phead->pnext;phead->pnext = pinsertnode;}return 0;
}

3. 补充知识点

其他实现方法：
- 递归法：通过递归到达链表末尾，再逐层反转指针，时间复杂度 O (n)，空间复杂度 O (n)（递归栈开销）。
- 三指针法：定义 prev、curr、next 三个指针，遍历过程中依次修改指针方向，空间复杂度 O (1)。
时间与空间复杂度：上述头插法实现的时间复杂度为 O (n)，空间复杂度为 O (1)，是最优的实现方式之一。
应用场景：链表反转可用于解决 “链表回文判断”“反转链表中的指定区间” 等扩展问题。

八、链表的排序：冒泡与选择排序

链表的排序与数组排序思路类似，但由于链表无法随机访问，排序算法的实现细节有所不同。

1. 冒泡排序

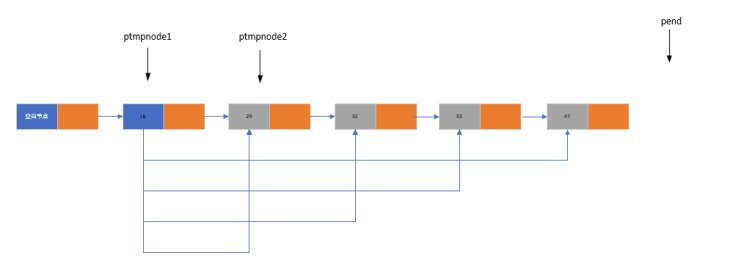
核心思想：通过相邻节点的比较和交换，使大的元素 “冒泡” 到链表末尾。
实现要点：
- 定义两个指针 ptmpnode1 和 ptmpnode2，分别指向相邻的两个节点
- 每次遍历比较相邻节点，若顺序错误则交换数据
- 引入 pend 指针记录已排序部分的末尾，减少无效比较
代码实现：

/* 链表的冒泡排序 */
int bubble_sort_linklist(linknode *phead) {linknode *ptmpnode1 = NULL;linknode *ptmpnode2 = NULL;linknode *pend = NULL;datatype tmpdata;if (NULL == phead->pnext || NULL == phead->pnext->pnext) {return 0; // 空链表或只有一个节点无需排序}while (1) {ptmpnode1 = phead->pnext;ptmpnode2 = phead->pnext->pnext;if (pend == ptmpnode2) {break; // 排序完成}while (ptmpnode2 != pend) {if (ptmpnode1->data > ptmpnode2->data) {// 交换数据tmpdata = ptmpnode1->data;ptmpnode1->data = ptmpnode2->data;ptmpnode2->data = tmpdata;}ptmpnode1 = ptmpnode1->pnext;ptmpnode2 = ptmpnode2->pnext;}pend = ptmpnode1; // 更新已排序末尾}return 0;
}

2. 选择排序

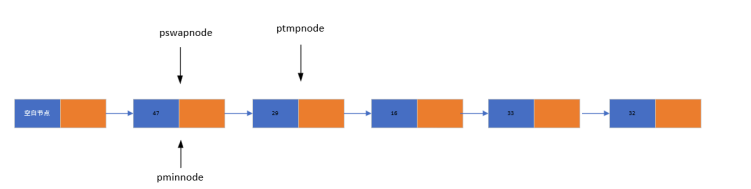
核心思想：每次从无序部分找到最小元素，与无序部分的第一个元素交换数据，使无序部分逐渐减少。
实现要点：
- 定义 pswapnode 指向无序部分的第一个节点
- 遍历无序部分，用 pminnode 记录最小元素节点
- 交换 pswapnode 与 pminnode 的数据，完成一次选择
代码实现：


/*链表的选择排序*/
int select_sort_linklist(linknode *phead)
{linknode *pswapnode = NULL; // 当前待交换位置的节点指针（未排序部分的起始节点）linknode *ptmpnode = NULL;  // 用于遍历未排序部分的临时指针linknode *pminnode = NULL;  // 指向当前最小值的节点指针datatype tmpdata;           // 临时存储节点数据的变量// 边界检查：链表为空或只有一个节点时无需排序if(phead->pnext == NULL || phead->pnext->pnext == NULL){return 0; // 直接返回，无需操作}pswapnode = phead->pnext;   // 初始化排序起始位置：指向首元节点（跳过头节点）// 外层循环：遍历链表直到倒数第二个节点（结束条件）while (pswapnode->pnext != NULL){pminnode = pswapnode;   // 初始化最小值节点为当前起始节点ptmpnode = pswapnode->pnext; // 从当前节点的下一个节点开始遍历// 内层循环：遍历未排序部分寻找最小值节点while(ptmpnode != NULL){// 比较当前节点值与最小值节点值if(ptmpnode->data < pminnode->data){pminnode = ptmpnode; // 更新最小值节点指针}ptmpnode = ptmpnode->pnext; // 移动到下一个待比较节点}// 如果最小值不在当前位置则交换数据if(pswapnode != pminnode){tmpdata = pswapnode->data;          // 暂存当前节点数据pswapnode->data = pminnode->data;   // 将最小值数据复制到当前位置pminnode->data = tmpdata;           // 将原数据存回最小值节点}pswapnode = pswapnode->pnext; // 移动起始位置到下一节点（缩小未排序范围）}return 0; // 排序完成，返回状态码
}

3. 补充知识点

效率分析：冒泡排序和选择排序的时间复杂度均为 O (n²)，适用于数据量较小的链表。对于大数据量，建议使用归并排序（时间复杂度 O (nlogn)），链表的归并排序无需额外空间存储临时数组，只需修改指针关系。
与数组排序的差异：链表排序仅交换数据域的值（或节点指针），无需移动整个节点的内存位置，因此数据交换的开销更小。
稳定性：冒泡排序是稳定排序（相等元素不交换位置），选择排序是不稳定排序（可能改变相等元素的相对顺序）。

九、链表的环问题：判断、环长与入口

链表的环问题是指链表中某个节点的指针指向了前面的节点，形成一个闭合的环，这会导致遍历操作无限循环，因此需要专门的方法解决。

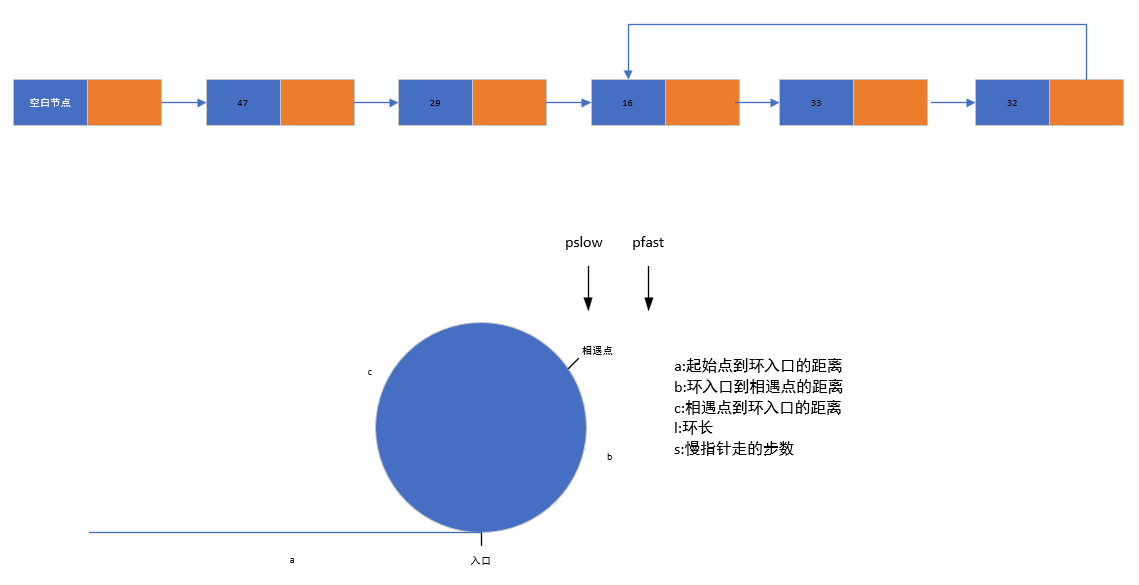
1. 判断链表是否有环

核心思想：使用快慢指针（快指针每次走 2 步，慢指针每次走 1 步）。若链表有环，两指针最终会在环内相遇；若无环，快指针会先到达末尾（NULL）。

2. 计算环长

实现思路：两指针相遇后，让其中一个指针继续前进并计数，当再次回到相遇点时，计数即为环的长度。

3. 查找环的入口

公式推导：设 a 为起始点到环入口的距离，b 为环入口到相遇点的距离，c 为相遇点到环入口的距离，环长 l = b + c。通过推导可得 a = c + (n-1)*l（n 为快指针绕环的圈数），即从起始点和相遇点同时出发的两个指针，会在环入口相遇。
实现思路：让一个指针从链表起始点出发，另一个指针从相遇点出发，两者每次走 1 步，相遇点即为环入口。

4. 综合代码实现

/*  1.判断链表是否有环 2.计算环长3.找到环的入口位置
*/
int circle_linklist(linknode *phead,int *pis_circle,int *pcirlen,linknode **ppnode)
{linknode *pfast = NULL;linknode *pslow = NULL;linknode *ptmpnode = NULL;linknode *pstartnode = NULL;int cnt = 1;/*判断是否有环*/pfast = phead->pnext;pslow = phead->pnext;while(1){pfast = pfast->pnext;if(NULL == pfast){break;}pfast = pfast->pnext;if(NULL == pfast){break;}pslow = pslow->pnext;if(pfast == pslow){break;;}}if (NULL == pfast){*pis_circle = 0;return 0;}else {*pis_circle = 1;}/* 统计环长 */ptmpnode = pslow->pnext;while (ptmpnode != pslow){cnt++;ptmpnode = ptmpnode->pnext;}*pcirlen = cnt;/* 找到环入口 */    pstartnode = phead->pnext;ptmpnode = pslow;while (pstartnode != ptmpnode){pstartnode = pstartnode->pnext;ptmpnode = ptmpnode->pnext;}*ppnode = ptmpnode;return 0;
}

十、双向链表：更灵活的双向访问

双向链表每个节点除了数据域，还包含两个指针域（前驱指针 ppre 和后继指针 pnext），可实现双向遍历，弥补了单向链表的不足。

1. 节点定义

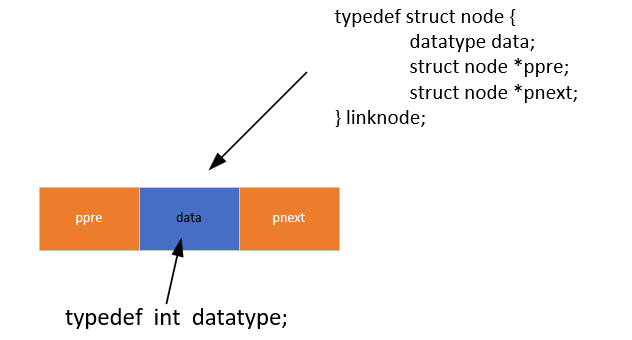
双向链表是一种每个节点除了存储数据外，还包含两个指针的线性数据结构：一个指针（ppre）指向前一个节点，另一个指针（pnext）指向后一个节点。这种结构允许我们从任意节点出发，既可以向前遍历，也可以向后遍历，弥补了单向链表只能单向访问的局限性。

与单向链表相比，双向链表的核心差异在于多了一个前驱指针，这使得它在插入、删除操作中不需要像单向链表那样依赖前驱节点的跟踪，从而提升了操作效率。

/* 节点存放数据的类型 */
typedef int datatype;/* 节点类型 */
typedef struct node {datatype data;       // 存放数据的空间struct node *ppre;   // 指向当前节点的前一个节点struct node *pnext;  // 指向当前节点的后一个节点
} linknode;

data：用于存储具体的数据，可以是 int、float 等任意类型，此处以 int 为例；
ppre：前驱指针，指向当前节点的前一个节点，若当前节点是第一个有效节点，则ppre为NULL；
pnext：后继指针，指向当前节点的后一个节点，若当前节点是最后一个有效节点，则pnext为NULL。

2. 双向链表的基本操作

1. 创建空双向链表

创建空双向链表的核心是初始化一个头节点（空白节点），头节点不存储有效数据，主要用于统一链表操作（如插入、删除的逻辑）。步骤如下：

申请一块内存空间作为头节点；
将头节点的ppre和pnext都初始化为NULL（表示暂时没有前驱和后继节点）；
返回头节点的地址。

代码实现：

linknode *create_empty_linklist(void) {linknode *ptmpnode = NULL;// 申请节点空间ptmpnode = malloc(sizeof(linknode));if (NULL == ptmpnode) {perror("fail to malloc");return NULL;}// 初始化前驱和后继指针为NULLptmpnode->ppre = NULL;ptmpnode->pnext = NULL;return ptmpnode;
}

注意：头节点的ppre始终为NULL（因为它是链表的起点），而pnext初始为NULL（表示链表为空）。

2. 头插法插入节点

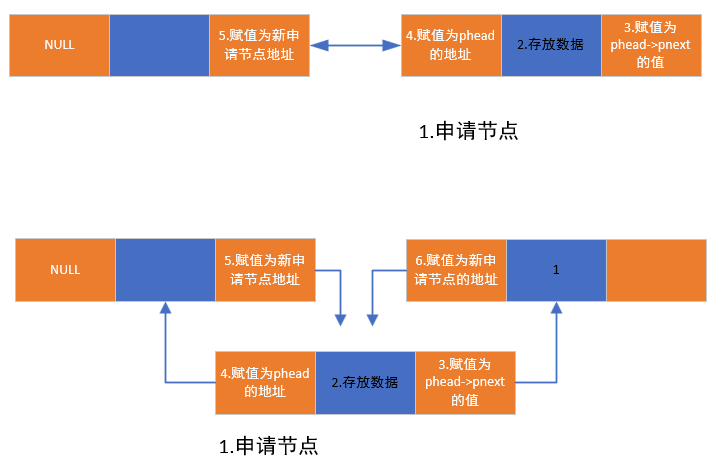
头插法是指在链表的头部（头节点之后）插入新节点，步骤如下：

申请新节点空间，并存入数据；
新节点的pnext指向头节点当前的pnext（即原第一个有效节点）；
新节点的ppre指向头节点（因为新节点的前驱是头节点）；
若头节点原本有后继节点（即原链表非空），则原第一个有效节点的ppre需要指向新节点；
头节点的pnext更新为新节点的地址

代码实现：

int insert_head_linklist(linknode *phead, datatype tmpdata) {if (NULL == phead) {printf("链表头节点为空，无法插入\n");return -1;}// 1. 申请新节点linknode *ptmpnode = malloc(sizeof(linknode));if (NULL == ptmpnode) {perror("fail to malloc");return -1;}// 2. 存入数据ptmpnode->data = tmpdata;// 3. 新节点的pnext指向头节点的pnext（原第一个有效节点）ptmpnode->pnext = phead->pnext;// 4. 新节点的ppre指向头节点ptmpnode->ppre = phead;// 5. 若原链表非空，更新原第一个有效节点的ppreif (phead->pnext != NULL) {phead->pnext->ppre = ptmpnode;}// 6. 头节点的pnext指向新节点phead->pnext = ptmpnode;return 0;
}

优势：相比单向链表的头插法，双向链表需要额外处理原第一个节点的ppre，但这确保了前驱指针的正确性，为后续双向遍历提供支持。

3. 遍历链表

双向链表支持向前遍历和向后遍历两种方式：

向后遍历：从第一个有效节点（phead->pnext）开始，通过pnext依次访问每个节点，直到pnext为NULL；
向前遍历：从最后一个有效节点（需先找到，即pnext为NULL的节点）开始，通过ppre依次访问每个节点，直到ppre为NULL（头节点）。

向后遍历代码实现：

void show_linklist(linknode *phead) {if (NULL == phead || phead->pnext == NULL) {printf("链表为空\n");return;}linknode *ptmpnode = phead->pnext;printf("链表元素（向后遍历）：");while (ptmpnode != NULL) {printf("%d ", ptmpnode->data);ptmpnode = ptmpnode->pnext;}printf("\n");
}

向前遍历代码实现（需先找到尾节点）：

void show_reverse_linklist(linknode *phead) {if (NULL == phead || phead->pnext == NULL) {printf("链表为空\n");return;}// 找到尾节点（pnext为NULL的节点）linknode *ptmpnode = phead->pnext;while (ptmpnode->pnext != NULL) {ptmpnode = ptmpnode->pnext;}printf("链表元素（向前遍历）：");while (ptmpnode != phead) {printf("%d ", ptmpnode->data);ptmpnode = ptmpnode->ppre;}printf("\n");
}

应用：双向遍历在需要反复前后查看数据的场景中非常实用，例如文本编辑器的光标移动、浏览器的历史记录浏览等。

4. 查找节点

查找操作是根据目标数据找到对应的节点，步骤与单向链表类似，但双向链表可根据数据位置选择从头部或尾部开始查找（若已知大致范围），提升效率。

代码实现（从头部向后查找）：

linknode *find_linklist(linknode *phead, datatype tmpdata) {if (NULL == phead || phead->pnext == NULL) {return NULL; // 链表为空，返回NULL}linknode *ptmpnode = phead->pnext;while (ptmpnode != NULL) {if (ptmpnode->data == tmpdata) {return ptmpnode; // 找到目标节点，返回地址}ptmpnode = ptmpnode->pnext;}return NULL; // 未找到
}

优化：若已知目标数据可能在链表后半段，可先找到尾节点，通过ppre向前查找，减少遍历次数。

5. 修改节点数据

修改操作是先通过查找找到目标节点，再更新其data值，代码如下：

int update_linklist(linknode *phead, datatype olddata, datatype newdata) {if (NULL == phead || phead->pnext == NULL) {return -1; // 链表为空，无法修改}linknode *ptmpnode = find_linklist(phead, olddata);if (NULL != ptmpnode) {ptmpnode->data = newdata; // 找到节点，更新数据return 0;}return -1; // 未找到目标节点
}

作业：

/*更新指定元素的值*/
int  update_linklist(linknode *phead,datatype olddata,datatype newdata)
{linknode *ptmpnode = NULL;ptmpnode = phead->pnext;while(ptmpnode != NULL){if(ptmpnode->data == olddata){ptmpnode->data = newdata;}ptmpnode = ptmpnode->pnext;}return 0;
}

优势：若修改后需要调整节点位置，双向链表可通过ppre和pnext快速关联前后节点，比单向链表更灵活。

6. 删除节点

删除操作是双向链表的核心优势所在。由于每个节点都有ppre指针，无需像单向链表那样从头遍历寻找前驱节点，直接通过ppre即可获取前驱，步骤如下：

找到要删除的节点pdel；
获取pdel的前驱节点pre（pdel->ppre）和后继节点next（pdel->pnext）；
让pre->pnext指向next（断开前驱与pdel的联系）；
若next不为NULL，让next->ppre指向pre（断开后继与pdel的联系）；
释放pdel的内存空间。

代码实现：

仅用一个指针

/*删除指定节点*/
int delete_linklist(linknode *phead,datatype tmpdata)
{linknode *ptmpnode = NULL;ptmpnode = phead->pnext;while(NULL != ptmpnode){if(ptmpnode->data == tmpdata){ptmpnode->ppre->pnext = ptmpnode->pnext;if(ptmpnode->pnext != NULL){ptmpnode->pnext->ppre = ptmpnode->ppre;}free(ptmpnode);}ptmpnode = ptmpnode->pnext;       }return 0;
}

效率：单向链表删除节点的时间复杂度为 O (n)（需遍历找前驱），而双向链表仅需 O (1)（直接通过ppre获取前驱），效率显著提升。

7. 销毁链表

销毁链表需要释放所有节点（包括头节点）的内存，避免内存泄漏，步骤如下：

定义指针ptmp指向当前要释放的节点，pnext记录下一个节点；
从第一个有效节点开始，依次释放每个节点；
最后释放头节点，并将头指针设为NULL。

代码实现：

/*销毁链表*/
void destory_linklist(linknode **pphead)
{linknode *ptmpnode = NULL;linknode *next = NULL;ptmpnode = *pphead;next = *pphead;while(next != NULL){  next = ptmpnode->pnext;// printf("%d ",ptmpnode->data);  （对）free(ptmpnode);ptmpnode = next; // printf("%d ",ptmpnode->data);  （段错误：不能放到这里）}*pphead = NULL;// 避免野指针return;
}

注意：销毁时需通过二级指针pphead将头指针置空，防止后续误用已释放的内存。