风光储综合能源系统双层优化规划设计【MATLAB模型实现】
本模型基于双层优化框架,利用KKT条件、大M法、对偶理论求解,专注于综合能源系统(微电网)多电源容量优化配置的模型介绍。代码采用CPLEX求解器,注释详尽,非常适合新手学习该类问题的建模与求解思路。
模型总体原理:
该模型的核心思想是将复杂的综合能源系统规划问题分解为两个相互关联的决策层面:
-
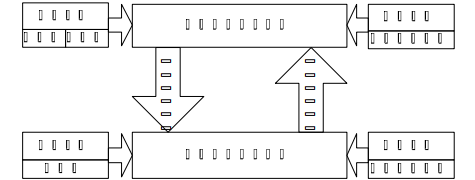
上层规划问题 (Investment/Planning Level): 负责长期投资决策。目标是确定系统中各类能源设备(如光伏PV、风机WT、储能ESS等)的最佳安装容量,使得整个规划周期内的总成本(设备投资成本 + 运行维护成本)最低。
-
下层运行问题 (Operation/Dispatch Level): 负责短期运行决策。在给定的设备容量(由上层的决策变量决定)下,目标是优化系统在一个典型运行周期(如一天、一周)内的运行策略(如发电机出力、储能充放电、购售电),使得该周期内的运行成本(购电成本 + 售电收益 + 燃料成本(如有燃气轮机)+ 其他可变运行成本)最低。
这两个层级通过容量变量紧密耦合:
-
上层的容量决策 (
Cap_PV,Cap_WT,Cap_ESS等) 是下层运行优化问题的输入参数或约束条件。 -
下层的运行成本是上层总成本目标函数的重要组成部分。
求解策略: 直接求解双层优化问题通常非常困难。该模型采用数学变换将其转化为一个单层混合整数线性规划 (MILP) 问题:
-
利用KKT条件: 将下层运行优化问题(通常是一个线性规划LP)的最优性条件(KKT条件)写出来。KKT条件包含:
-
原始可行性: 下层运行约束必须满足。
-
对偶可行性: 下层拉格朗日函数的梯度条件。
-
互补松弛条件: 原始约束和对偶变量之间满足互补关系。
-
-
处理互补松弛条件 (使用大M法): 互补松弛条件是双线性项(对偶变量 * 约束松弛量),是非凸的。大M法引入辅助二元变量和足够大的常数
M,将这些非线性互补条件等价地转化为一组线性约束和二元变量约束。 -
整合目标函数: 将上层目标函数(包含投资成本和下层运行成本)与经过KKT条件和大M法转换后的下层约束整合到一起,形成一个大型的单层MILP问题。
-
对偶理论(辅助): 在推导KKT条件中的对偶可行性部分时,会用到线性规划的对偶理论,以确保转换的正确性。
最终模型是一个包含连续变量、二元变量、线性目标函数和线性约束的MILP问题,可以使用高效的商业求解器如CPLEX进行求解。
部分程序实例:
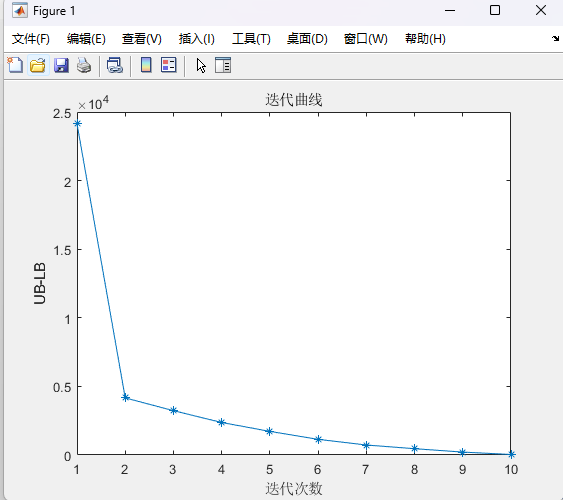
%% 考虑四种典型日下的双层规划clcclearwarning offclose alltic%% 设置参数canshu;%% 初始值%% 上层%初始折现成本+投资成本+购售电成本和燃料成本 +运维成本%LB为初始折现成本+投资成本+购售电成本+燃料成本 +运维成本%yita购售电成本+燃料成本+运维成本[yita,LB,ee_bat_int, p_wt_int,p_pv_int,p_g_int] = UP_1(rp,rbat,rPV,rWT,rG);%% 下层%UB为上层(折现成本+投资成本)+下层(购售电成本+燃料成本 +运维成本)[p_wt,p_pv,p_load,x,UB,p_g,p_ch,p_dis,p_buy,p_sell] = DOWN_(ee_bat_int,p_wt_int,p_pv_int,p_g_int,LB,yita);%UB1为初始上层(折现成本+投资成本)+下层(购售电成本+燃料成本 +运维成本)UB1 = UB;%% p为上层(购售电成本+燃料成本 +运维成本)与下层(购售电成本+燃料成本 +运维成本)差p(1)= UB - LB;e=100;%收敛度%% 开始迭代for k=1:Imax%% 上层 在已知光伏,风电,负荷出力(由下层传递到上层)计算初始折现成本+投资成本+购售电成本和燃料成本 +运维成本(求最小值)[yita,LB,ee_bat_int,p_wt_int,p_pv_int,p_g_int] = UP_2(p_wt,p_pv,p_load);%MP迭代%% 下层 已知(折现成本+投资成本,由上层传递到下层)+计算(购售电成本+燃料成本 +运维成本)[p_wt,p_pv,p_load,x,UB,p_g,p_ch,p_dis,p_buy,p_sell] = DOWN_(ee_bat_int,p_wt_int,p_pv_int,p_g_int,LB,yita);%SP迭代UB = min(UB1,UB);%取UB较小值%% p为上层(购售电成本+燃料成本 +运维成本)与下层(购售电成本+燃料成本 +运维成本)差p(k+1) = UB-LB;%判断是否收敛if abs(p(k+1))<=ebreakendend%% 输出结果%储能,购电,风电,光伏,负荷,燃机p_wtp_pvp_loadp_gp_chp_disp_buyp_selltoc%% 画图%% 迭代figure;plot(p,'-*')xlabel('迭代次数')ylabel('UB-LB')title('迭代曲线')%% 典型日1figurehold onpositive=[p_wt(:,1),p_pv(:,1),p_g(:,1),p_dis(:,1),p_buy(:,1)];negative=[-p_ch(:,1),-p_sell(:,1)];bar(positive,'stack')bar(negative,'stack')plot(p_load(:,1),'-d')ylabel('出力/kw')xlabel('时间/小时')title('典型日1调度曲线')legend('光伏','风电','燃机','电池放电','购电','电池充电','售电','居民负荷')输出结果:
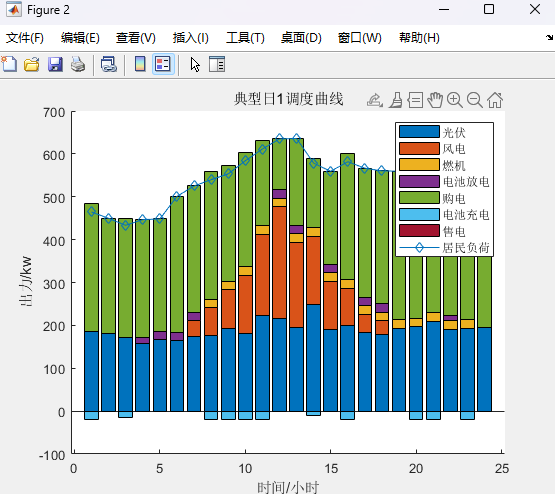
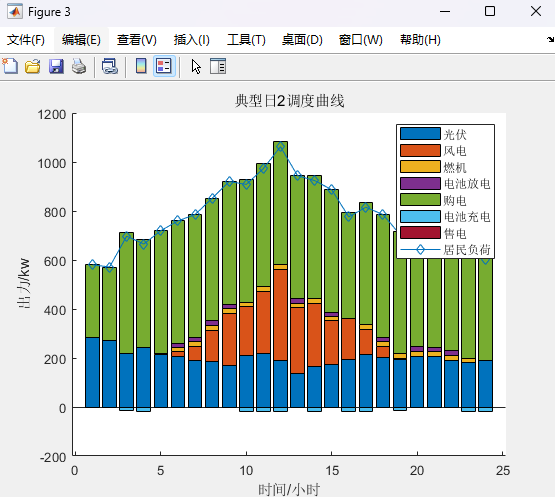
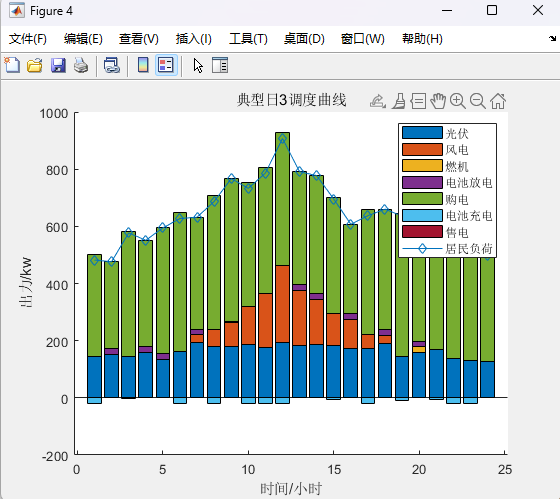
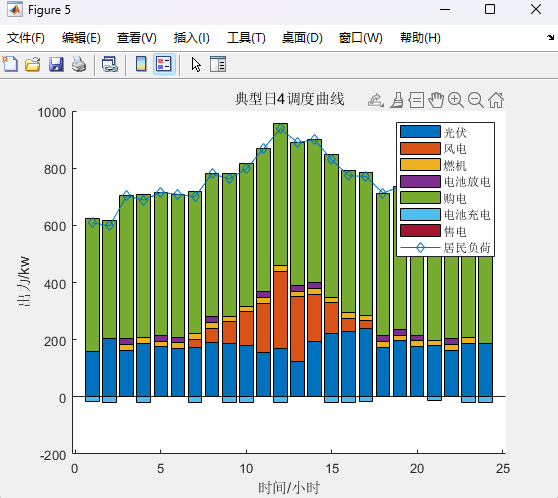
总结:
该模型通过双层优化结构清晰地区分了长期规划(容量决策)和短期运行(调度决策)。利用KKT条件刻画下层最优性,借助大M法处理非线性的互补松弛条件,并运用对偶理论确保转换正确,最终将复杂的双层问题转化为一个可被CPLEX高效求解的单层混合整数线性规划(MILP)问题。其输出提供了微电网建设的最佳多电源容量配置方案 (Cap_PV, Cap_WT, Cap_ESS) 以及在该配置下成本最优的运行策略。注释齐全的代码为学习这种建模与求解方法提供了宝贵的实践材料。
仿真程序模型详情见原文链接:
https://mp.weixin.qq.com/s/kX85ZaK1o_B35QHQRtq_Cw
