当前位置：首页 > news >正文
轨道追逃博弈仿真

news 2025/8/3 21:47:17
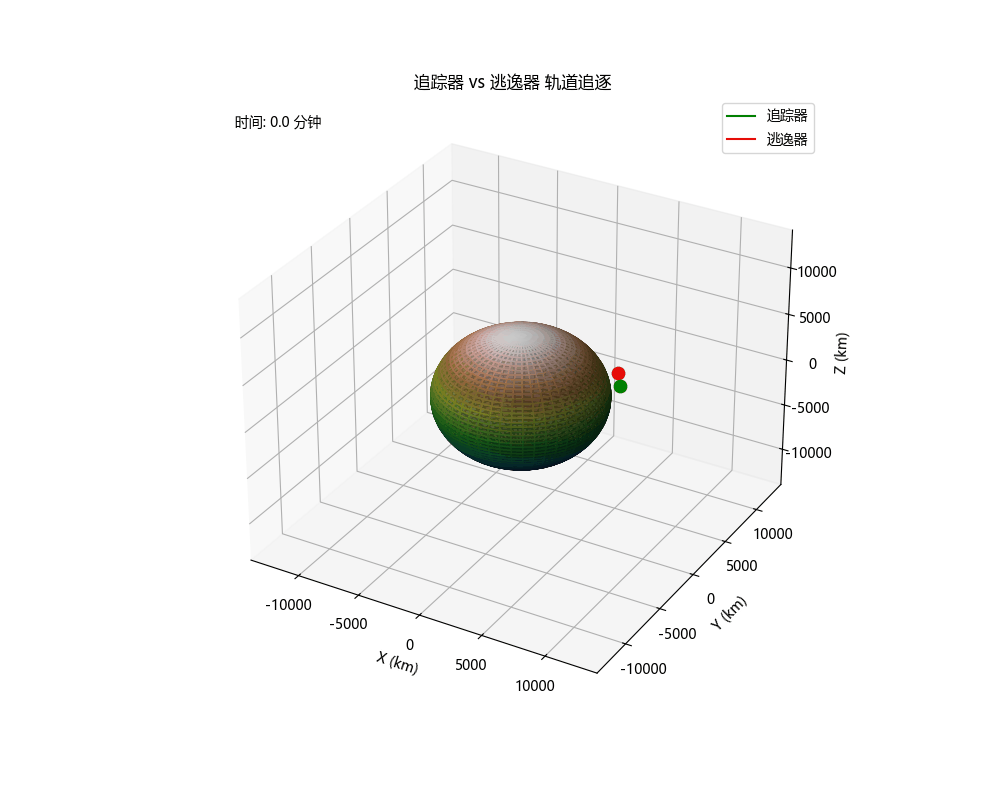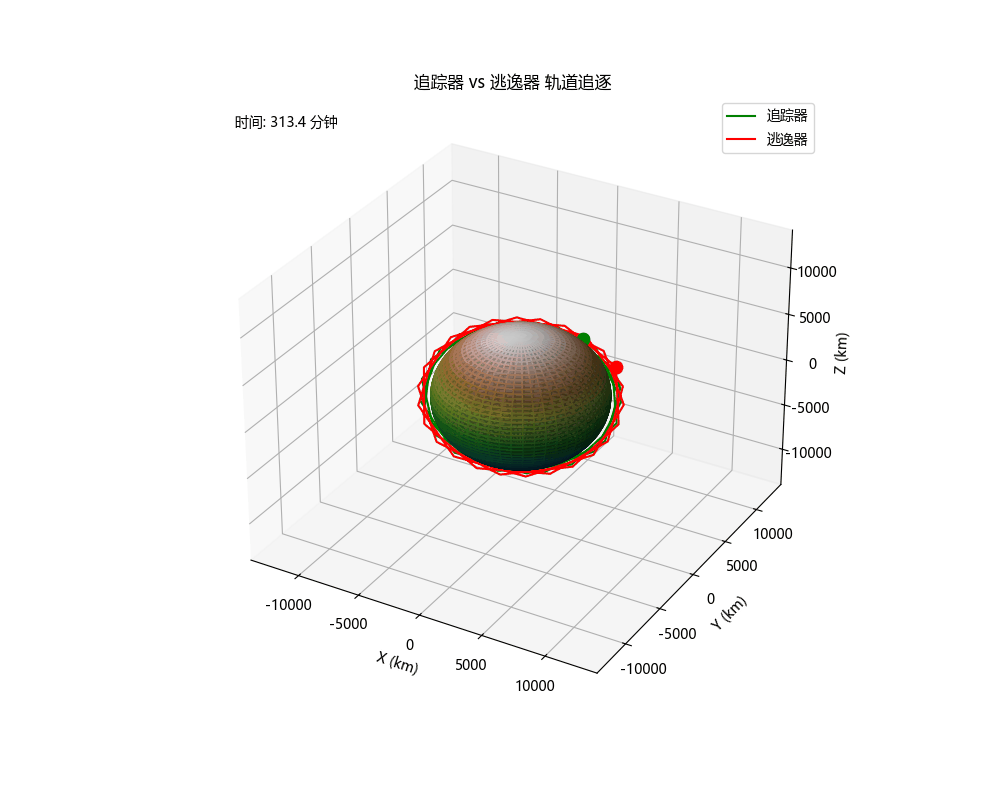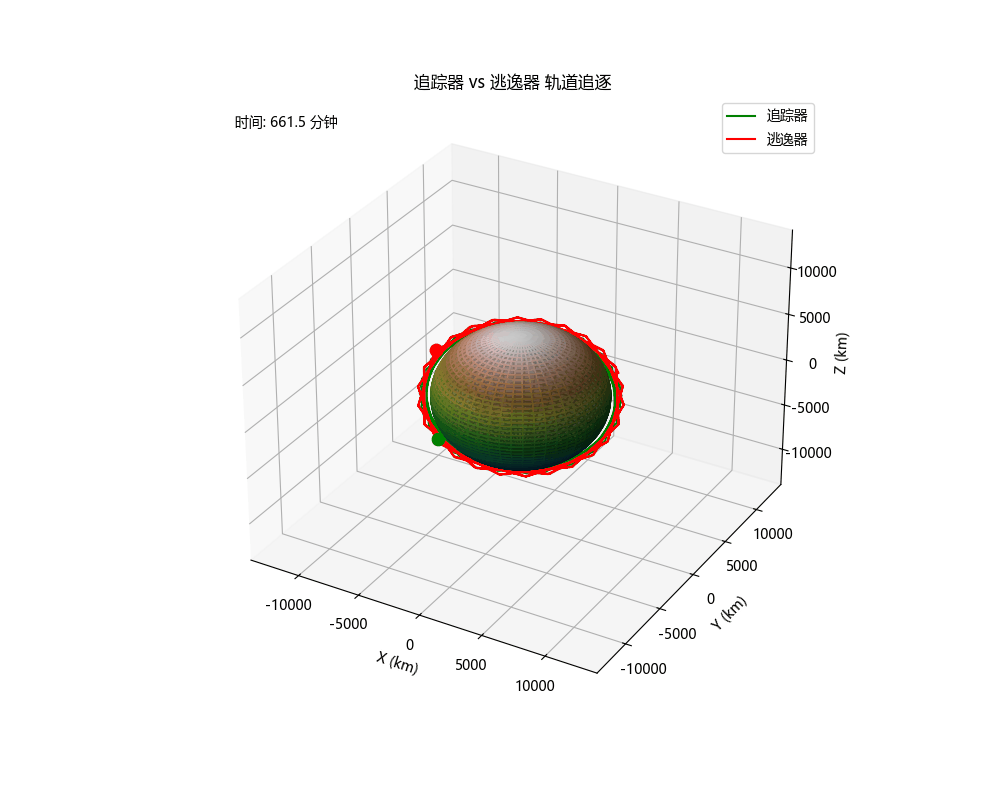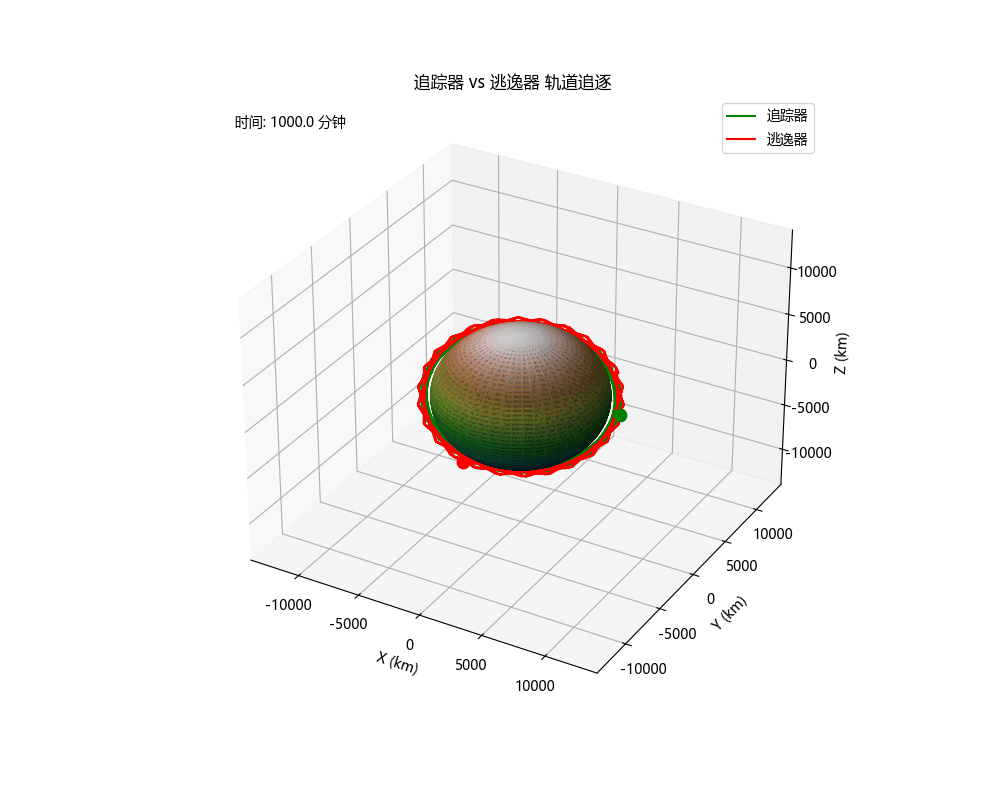
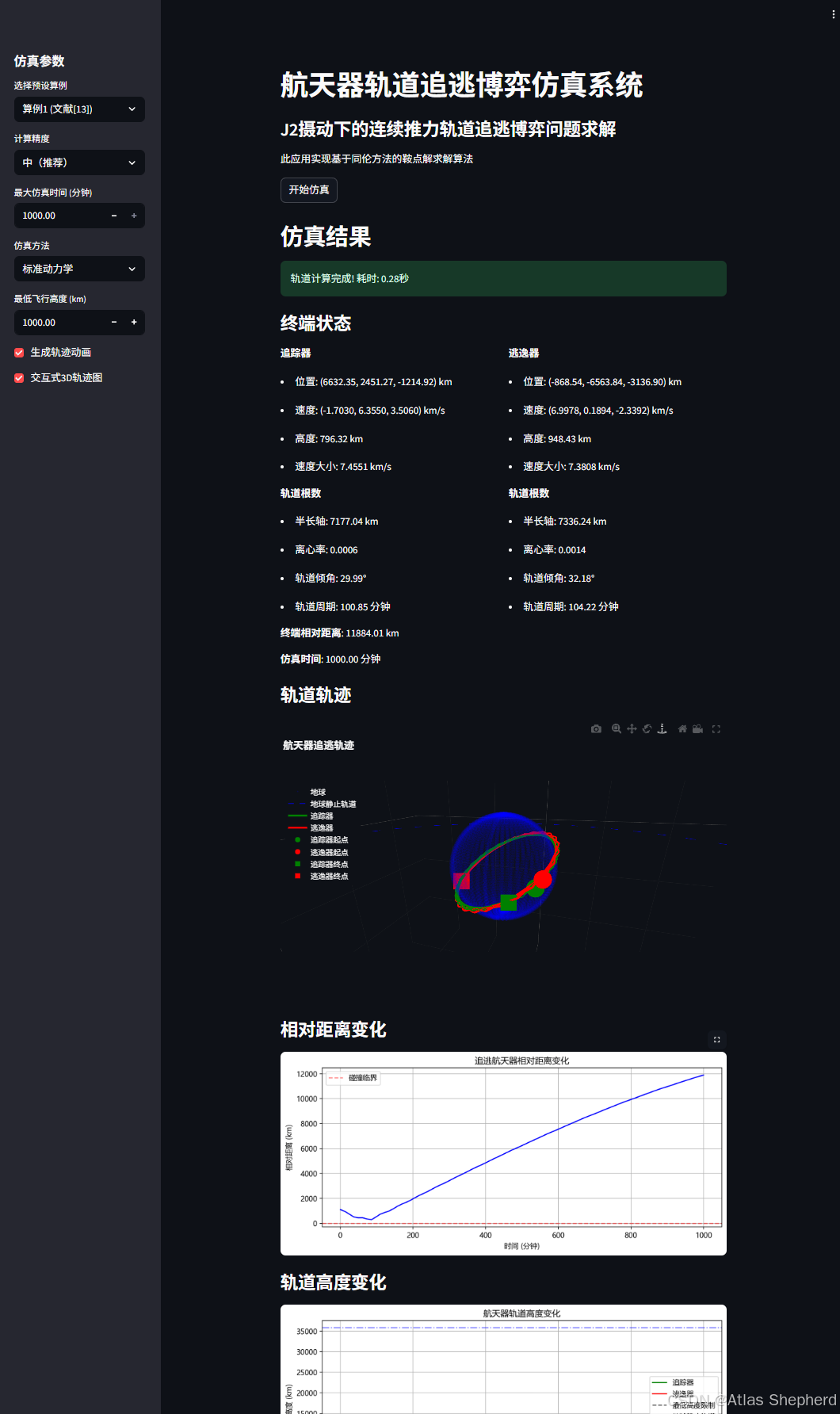
终端状态

追踪器
位置: (6632.35, 2451.27, -1214.92) km
速度: (-1.7030, 6.3550, 3.5060) km/s
高度: 796.32 km
速度大小: 7.4551 km/s
轨道根数
半长轴: 7177.04 km
离心率: 0.0006
轨道倾角: 29.99°
轨道周期: 100.85 分钟
逃逸器
位置: (-868.54, -6563.84, -3136.90) km
速度: (6.9978, 0.1894, -2.3392) km/s
高度: 948.43 km
速度大小: 7.3808 km/s
轨道根数
半长轴: 7336.24 km
离心率: 0.0014
轨道倾角: 32.18°
轨道周期: 104.22 分钟
终端相对距离: 11884.01 km
仿真时间: 1000.00 分钟
import numpy as np
import streamlit as st
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import sys
import matplotlib as mpl
import time
from io import BytesIO
import pandas as pd
import os
import matplotlib.animation as animation
from matplotlib.colors import LightSource
import plotly.graph_objects as go  # 添加Plotly支持
import tempfile
from pathlib import Path# 设置中文字体支持
try:# 尝试使用支持更广泛字符的字体plt.rcParams['font.sans-serif'] = ['Microsoft YaHei', 'SimHei', 'KaiTi', 'Arial Unicode MS']plt.rcParams['axes.unicode_minus'] = False
except:st.warning("中文字体设置失败，部分中文可能无法正常显示")# 物理常数
MU = 3.986004418e5  # 地球引力常数 (km³/s²)
RE = 6378.137  # 地球赤道半径 (km)
J2 = 1.0826359e-3  # J2摄动系数
MIN2SEC = 60  # 分钟转秒
GEO_ALTITUDE = 35786.0  # 地球静止轨道高度 (km) - 修正为浮点数class Spacecraft:def __init__(self, position, velocity, thrust_accel, name="Spacecraft"):self.r = np.array(position)  # 位置矢量 (km)self.v = np.array(velocity)  # 速度矢量 (km/s)self.thrust = thrust_accel  # 推力加速度 (km/s²)self.state = np.hstack([self.r, self.v])self.name = nameself.control_history = []self.time_history = []self.current_control = np.zeros(3)self.orbital_elements = Nonedef update_state(self, state):self.r = state[:3]self.v = state[3:]self.state = stateself.calculate_orbital_elements()def get_altitude(self):return np.linalg.norm(self.r) - REdef get_speed(self):return np.linalg.norm(self.v)def calculate_orbital_elements(self):"""计算轨道根数"""r = np.linalg.norm(self.r)v = np.linalg.norm(self.v)# 角动量矢量h_vec = np.cross(self.r, self.v)h = np.linalg.norm(h_vec)# 节点矢量n_vec = np.cross([0, 0, 1], h_vec)n = np.linalg.norm(n_vec)# 离心率矢量e_vec = ((v ** 2 - MU / r) * self.r - np.dot(self.r, self.v) * self.v) / MUe = np.linalg.norm(e_vec)# 半长轴a = 1 / (2 / r - v ** 2 / MU)# 轨道倾角i = np.arccos(h_vec[2] / h)# 升交点赤经omega = np.arccos(n_vec[0] / n)if n_vec[1] < 0:omega = 2 * np.pi - omega# 近地点角距w = np.arccos(np.dot(n_vec, e_vec) / (n * e))if e_vec[2] < 0:w = 2 * np.pi - w# 真近点角f = np.arccos(np.dot(e_vec, self.r) / (e * r))if np.dot(self.r, self.v) < 0:f = 2 * np.pi - fself.orbital_elements = {'a': a,  # 半长轴 (km)'e': e,  # 离心率'i': i * 180 / np.pi,  # 轨道倾角 (度)'ω': omega * 180 / np.pi,  # 升交点赤经 (度)'w': w * 180 / np.pi,  # 近地点角距 (度)'f': f * 180 / np.pi  # 真近点角 (度)}def get_orbital_period(self):"""计算轨道周期 (分钟)"""if self.orbital_elements:a = self.orbital_elements['a']T = 2 * np.pi * np.sqrt(a ** 3 / MU)  # 周期(秒)return T / 60  # 转换为分钟return 0class TwoBodyProblem:def __init__(self, pursuer, evader):self.pursuer = pursuerself.evader = evaderself.states = np.hstack([pursuer.state, evader.state])self.simulation_time = Noneself.status = "尚未运行"def dynamics(self, t, y):# 解包状态向量 [x_p, y_p, z_p, vx_p, vy_p, vz_p, x_e, y_e, z_e, vx_e, vy_e, vz_e]x_p, y_p, z_p, vx_p, vy_p, vz_p = y[:6]x_e, y_e, z_e, vx_e, vy_e, vz_e = y[6:12]# 计算追踪器加速度 (包含J2摄动)r_p = np.array([x_p, y_p, z_p])r_mag_p = np.linalg.norm(r_p)# 检查是否坠毁if r_mag_p <= RE:self.status = f"{self.pursuer.name}已坠毁!"return np.zeros(12)a_gravity_p = -MU * r_p / r_mag_p ** 3# J2摄动加速度tx = x_p / r_mag_pty = y_p / r_mag_ptz = z_p / r_mag_pfactor = (3 * J2 * MU * RE ** 2) / (2 * r_mag_p ** 4)a_j2x = factor * (5 * tz ** 2 - 1) * txa_j2y = factor * (5 * tz ** 2 - 1) * tya_j2z = factor * (5 * tz ** 2 - 3) * tza_total_p = a_gravity_p + np.array([a_j2x, a_j2y, a_j2z])# 计算逃逸器加速度 (包含J2摄动)r_e = np.array([x_e, y_e, z_e])r_mag_e = np.linalg.norm(r_e)# 检查是否坠毁if r_mag_e <= RE:self.status = f"{self.evader.name}已坠毁!"return np.zeros(12)a_gravity_e = -MU * r_e / r_mag_e ** 3tx_e = x_e / r_mag_ety_e = y_e / r_mag_etz_e = z_e / r_mag_efactor_e = (3 * J2 * MU * RE ** 2) / (2 * r_mag_e ** 4)a_j2x_e = factor_e * (5 * tz_e ** 2 - 1) * tx_ea_j2y_e = factor_e * (5 * tz_e ** 2 - 1) * ty_ea_j2z_e = factor_e * (5 * tz_e ** 2 - 3) * tz_ea_total_e = a_gravity_e + np.array([a_j2x_e, a_j2y_e, a_j2z_e])# 获取当前控制策略u_p = self.pursuer.current_controlu_e = self.evader.current_control# 记录控制历史和时间self.pursuer.control_history.append(u_p.copy())self.evader.control_history.append(u_e.copy())self.pursuer.time_history.append(t)self.evader.time_history.append(t)# 添加推力加速度dvdt_p = a_total_p + u_pdvdt_e = a_total_e + u_e# 返回状态导数return np.hstack([vx_p, vy_p, vz_p, dvdt_p[0], dvdt_p[1], dvdt_p[2],vx_e, vy_e, vz_e, dvdt_e[0], dvdt_e[1], dvdt_e[2]])class SimpleControlSolver:def __init__(self, spacecraft, is_pursuer=True):self.sc = spacecraftself.is_pursuer = is_pursuerdef update(self, state_other, dt):# 简单控制策略：追踪器朝目标方向加速，逃逸器垂直逃离if self.is_pursuer:# 追踪器控制：朝目标方向施加最大推力direction = state_other[:3] - self.sc.rdirection_norm = np.linalg.norm(direction)if direction_norm > 1e-3:direction /= direction_normself.sc.current_control = direction * self.sc.thrustelse:# 逃逸器控制：垂直轨道面方向逃离v_direction = self.sc.v / np.linalg.norm(self.sc.v)r_direction = self.sc.r / np.linalg.norm(self.sc.r)# 创建垂直轨道面的向量normal = np.cross(r_direction, v_direction)normal_norm = np.linalg.norm(normal)if normal_norm > 1e-3:normal /= normal_normself.sc.current_control = normal * self.sc.thrustdef plot_3d_trajectory(t, states, pursuer_name="追踪器", evader_name="逃逸器"):fig = plt.figure(figsize=(10, 8))ax = fig.add_subplot(111, projection='3d')# 绘制地球u = np.linspace(0, 2 * np.pi, 100)v = np.linspace(0, np.pi, 100)x = RE * np.outer(np.cos(u), np.sin(v))y = RE * np.outer(np.sin(u), np.sin(v))z = RE * np.outer(np.ones(np.size(u)), np.cos(v))# 添加光照效果ls = LightSource(azdeg=315, altdeg=45)rgb = ls.shade(z, plt.cm.gist_earth, vert_exag=0.1, blend_mode='soft')ax.plot_surface(x, y, z, rstride=1, cstride=1, facecolors=rgb, alpha=0.8)# 提取轨迹x_p = states[0]y_p = states[1]z_p = states[2]x_e = states[6]y_e = states[7]z_e = states[8]# 绘制轨迹ax.plot(x_p, y_p, z_p, 'g-', linewidth=2, label=pursuer_name)ax.plot(x_e, y_e, z_e, 'r-', linewidth=2, label=evader_name)# 标记起点和终点ax.scatter(x_p[0], y_p[0], z_p[0], c='g', s=100, marker='o', label=f"{pursuer_name}起点")ax.scatter(x_e[0], y_e[0], z_e[0], c='r', s=100, marker='o', label=f"{evader_name}起点")ax.scatter(x_p[-1], y_p[-1], z_p[-1], c='g', s=100, marker='s', label=f"{pursuer_name}终点")ax.scatter(x_e[-1], y_e[-1], z_e[-1], c='r', s=100, marker='s', label=f"{evader_name}终点")# 绘制地球静止轨道geo_radius = RE + GEO_ALTITUDEu = np.linspace(0, 2 * np.pi, 100)x_geo = geo_radius * np.cos(u)y_geo = geo_radius * np.sin(u)ax.plot(x_geo, y_geo, np.zeros_like(u), 'b--', linewidth=0.8, alpha=0.5, label="地球静止轨道")# 设置坐标轴max_val = max(np.max(np.abs(states[:3])), np.max(np.abs(states[6:9])), geo_radius * 1.2) * 1.1ax.set_xlim([-max_val, max_val])ax.set_ylim([-max_val, max_val])ax.set_zlim([-max_val, max_val])ax.set_xlabel('X (km)')ax.set_ylabel('Y (km)')ax.set_zlabel('Z (km)')ax.set_title('航天器追逃轨迹')# 设置等比例ax.set_box_aspect([1, 1, 1])plt.legend(loc='upper right')return figdef create_animation(t, states, pursuer_name="追踪器", evader_name="逃逸器", fps=30):"""创建轨迹动画"""fig = plt.figure(figsize=(10, 8))ax = fig.add_subplot(111, projection='3d')# 计算合适的采样间隔total_frames = min(int(t[-1] * fps), 300)  # 最大300帧step = max(len(t) // total_frames, 1)# 绘制地球u = np.linspace(0, 2 * np.pi, 50)v = np.linspace(0, np.pi, 50)x = RE * np.outer(np.cos(u), np.sin(v))y = RE * np.outer(np.sin(u), np.sin(v))z = RE * np.outer(np.ones(np.size(u)), np.cos(v))ls = LightSource(azdeg=315, altdeg=45)rgb = ls.shade(z, plt.cm.gist_earth, vert_exag=0.1, blend_mode='soft')ax.plot_surface(x, y, z, rstride=1, cstride=1, facecolors=rgb, alpha=0.7)# 设置坐标轴范围max_val = max(np.max(np.abs(states[:3])), np.max(np.abs(states[6:9])), RE * 2) * 1.1ax.set_xlim([-max_val, max_val])ax.set_ylim([-max_val, max_val])ax.set_zlim([-max_val, max_val])ax.set_xlabel('X (km)')ax.set_ylabel('Y (km)')ax.set_zlabel('Z (km)')# 创建轨迹点和标记line_p, = ax.plot([], [], [], 'g-', linewidth=1.5)line_e, = ax.plot([], [], [], 'r-', linewidth=1.5)point_p = ax.scatter([], [], [], c='g', s=80, marker='o')point_e = ax.scatter([], [], [], c='r', s=80, marker='o')# 文本对象显示时间time_text = ax.text2D(0.05, 0.95, '', transform=ax.transAxes)ax.set_title(f"{pursuer_name} vs {evader_name} 轨道追逐")plt.legend([line_p, line_e], [pursuer_name, evader_name], loc='upper right')# 初始化函数def init():line_p.set_data([], [])line_p.set_3d_properties([])line_e.set_data([], [])line_e.set_3d_properties([])point_p._offsets3d = ([], [], [])point_e._offsets3d = ([], [], [])time_text.set_text('')return line_p, line_e, point_p, point_e, time_text# 动画更新函数def update(frame):idx = frame * stepif idx >= len(t):idx = len(t) - 1x_p = states[0, :idx + 1]y_p = states[1, :idx + 1]z_p = states[2, :idx + 1]x_e = states[6, :idx + 1]y_e = states[7, :idx + 1]z_e = states[8, :idx + 1]line_p.set_data(x_p, y_p)line_p.set_3d_properties(z_p)line_e.set_data(x_e, y_e)line_e.set_3d_properties(z_e)point_p._offsets3d = ([x_p[-1]], [y_p[-1]], [z_p[-1]])point_e._offsets3d = ([x_e[-1]], [y_e[-1]], [z_e[-1]])time_text.set_text(f'时间: {t[idx] / MIN2SEC:.1f} 分钟')return line_p, line_e, point_p, point_e, time_text# 创建动画anim = animation.FuncAnimation(fig, update, frames=min(len(t) // step, total_frames),init_func=init, blit=True, interval=50)return animdef plot_interactive_3d(t, states, pursuer_name="追踪器", evader_name="逃逸器"):"""使用Plotly创建交互式3D轨迹图"""# 提取轨迹x_p = states[0]y_p = states[1]z_p = states[2]x_e = states[6]y_e = states[7]z_e = states[8]# 创建地球u = np.linspace(0, 2 * np.pi, 50)v = np.linspace(0, np.pi, 50)x_earth = RE * np.outer(np.cos(u), np.sin(v)).flatten()y_earth = RE * np.outer(np.sin(u), np.sin(v)).flatten()z_earth = RE * np.outer(np.ones(np.size(u)), np.cos(v)).flatten()# 创建地球静止轨道geo_radius = RE + GEO_ALTITUDEu = np.linspace(0, 2 * np.pi, 100)x_geo = geo_radius * np.cos(u)y_geo = geo_radius * np.sin(u)z_geo = np.zeros_like(u)# 创建轨迹图fig = go.Figure()# 添加地球fig.add_trace(go.Scatter3d(x=x_earth, y=y_earth, z=z_earth,mode='markers',marker=dict(size=2,color='blue',opacity=0.1),name='地球'))# 添加地球静止轨道fig.add_trace(go.Scatter3d(x=x_geo, y=y_geo, z=z_geo,mode='lines',line=dict(color='blue', width=1, dash='dash'),name='地球静止轨道'))# 添加追踪器轨迹fig.add_trace(go.Scatter3d(x=x_p, y=y_p, z=z_p,mode='lines',line=dict(color='green', width=3),name=pursuer_name))# 添加逃逸器轨迹fig.add_trace(go.Scatter3d(x=x_e, y=y_e, z=z_e,mode='lines',line=dict(color='red', width=3),name=evader_name))# 添加起点和终点fig.add_trace(go.Scatter3d(x=[x_p[0]], y=[y_p[0]], z=[z_p[0]],mode='markers',marker=dict(size=8, color='green'),name=f'{pursuer_name}起点'))fig.add_trace(go.Scatter3d(x=[x_e[0]], y=[y_e[0]], z=[z_e[0]],mode='markers',marker=dict(size=8, color='red'),name=f'{evader_name}起点'))fig.add_trace(go.Scatter3d(x=[x_p[-1]], y=[y_p[-1]], z=[z_p[-1]],mode='markers',marker=dict(size=8, color='green', symbol='square'),name=f'{pursuer_name}终点'))fig.add_trace(go.Scatter3d(x=[x_e[-1]], y=[y_e[-1]], z=[z_e[-1]],mode='markers',marker=dict(size=8, color='red', symbol='square'),name=f'{evader_name}终点'))# 设置布局max_val = max(np.max(np.abs(states[:3])), np.max(np.abs(states[6:9])), geo_radius * 1.2) * 1.1fig.update_layout(title='航天器追逃轨迹',scene=dict(xaxis=dict(title='X (km)', range=[-max_val, max_val]),yaxis=dict(title='Y (km)', range=[-max_val, max_val]),zaxis=dict(title='Z (km)', range=[-max_val, max_val]),aspectmode='cube'),legend=dict(yanchor="top", y=0.99, xanchor="left", x=0.01))return figdef validate_position(position):"""验证位置是否在地球内或太低"""r = np.linalg.norm(position)return r > RE + 100  # 至少高于地球表面100kmdef validate_velocity(position, velocity):"""验证速度是否合理"""v = np.linalg.norm(velocity)r = np.linalg.norm(position)escape_velocity = np.sqrt(2 * MU / r)  # 逃逸速度orbit_velocity = np.sqrt(MU / r)  # 圆形轨道速度return 0.6 * orbit_velocity < v < 1.5 * escape_velocitydef main():st.title("航天器轨道追逃博弈仿真系统")st.markdown("""### J2摄动下的连续推力轨道追逃博弈问题求解此应用实现基于同伦方法的鞍点解求解算法""")# 参数设置st.sidebar.header("仿真参数")# 预设算例选择cases = {"算例1 (文献[13])": {"p_name": "追踪器","p_pos": [5365.650, 4763.847, 0],"p_vel": [-4.286, 4.828, 3.727],"e_name": "逃逸器","e_pos": [4936.766, 5368.019, 813.001],"e_vel": [-4.909, 3.933, 3.842],"p_thrust": 0.12 * 9.80665 / 1000,"e_thrust": 0.03 * 9.80665 / 1000},"算例4 (文献[17])": {"p_name": "追踪器","p_pos": [-6598.212, 1163.443, 0],"p_vel": [-0.458, -2.598, 7.248],"e_name": "逃逸器","e_pos": [-6754.998, -3900.000, 0],"e_vel": [3.520, -6.097, 1.241],"p_thrust": 0.15 * 9.80665 / 1000,"e_thrust": 0.05 * 9.80665 / 1000},"低地球轨道追逐": {"p_name": "追踪卫星","p_pos": [7000, 0, 0],"p_vel": [0, 7.8, 0],"e_name": "目标卫星","e_pos": [7200, 0, 0],"e_vel": [0, 7.6, 0],"p_thrust": 0.05 * 9.80665 / 1000,"e_thrust": 0.03 * 9.80665 / 1000},"地球静止轨道": {"p_name": "服务飞船","p_pos": [42241, 0, 0],"p_vel": [0, 3.075, 0],"e_name": "失效卫星","e_pos": [43000, 0, 200],"e_vel": [0, 3.070, 0.01],"p_thrust": 0.02 * 9.80665 / 1000,"e_thrust": 0.01 * 9.80665 / 1000},"自定义参数": {"p_name": "追踪器","e_name": "逃逸器"}}selected_case = st.sidebar.selectbox("选择预设算例", list(cases.keys()))case = cases[selected_case]# 精度选项accuracy_level = st.sidebar.selectbox("计算精度",["低（快速模拟）", "中（推荐）", "高（精确结果）"],index=1)if accuracy_level == "低（快速模拟）":rtol, atol = 1e-4, 1e-6elif accuracy_level == "中（推荐）":rtol, atol = 1e-6, 1e-8else:  # 高精度rtol, atol = 1e-8, 1e-10# 设置参数输入if selected_case == "自定义参数":col1, col2 = st.sidebar.columns(2)with col1:st.subheader("追踪航天器")case["p_name"] = st.text_input("追踪器名称", "追踪器")p_x = st.number_input("追踪器 X (km)", value=5365.650)p_y = st.number_input("追踪器 Y (km)", value=4763.847)p_z = st.number_input("追踪器 Z (km)", value=0.0)p_vx = st.number_input("追踪器 Vx (km/s)", value=-4.286)p_vy = st.number_input("追踪器 Vy (km/s)", value=4.828)p_vz = st.number_input("追踪器 Vz (km/s)", value=3.727)case["p_thrust"] = st.number_input("追踪器推力 (g)", value=0.12) * 9.80665 / 1000with col2:st.subheader("逃逸航天器")case["e_name"] = st.text_input("逃逸器名称", "逃逸器")e_x = st.number_input("逃逸器 X (极坐标)", value=4936.766)e_y = st.number_input("逃逸器 Y (极坐标)", value=5368.019)e_z = st.number_input("逃逸器 Z (极坐标)", value=813.001)e_vx = st.number_input("逃逸器 Vx (km/s)", value=-4.909)e_vy = st.number_input("逃逸器 Vy (km/s)", value=3.933)e_vz = st.number_input("逃逸器 Vz (km/s)", value=3.842)case["e_thrust"] = st.number_input("逃逸器推力 (g)", value=0.03) * 9.80665 / 1000case["p_pos"] = [p_x, p_y, p_z]case["p_vel"] = [p_vx, p_vy, p_vz]case["e_pos"] = [e_x, e_y, e_z]case["e_vel"] = [e_vx, e_vy, e_vz]else:# 使用预设参数case["p_pos"] = case.get("p_pos", [5365.650, 4763.847, 0])case["p_vel"] = case.get("p_vel", [-4.286, 4.828, 3.727])case["e_pos"] = case.get("e_pos", [4936.766, 5368.019, 813.001])case["e_vel"] = case.get("e_vel", [-4.909, 3.933, 3.842])case["p_thrust"] = case.get("p_thrust", 0.12 * 9.80665 / 1000)case["e_thrust"] = case.get("e_thrust", 0.03 * 9.80665 / 1000)# 验证参数valid_p = validate_position(case["p_pos"]) and validate_velocity(case["p_pos"], case["p_vel"])valid_e = validate_position(case["e_pos"]) and validate_velocity(case["e_pos"], case["e_vel"])if not valid_p:st.sidebar.warning(f"追踪器初始位置或速度不合理，可能无法维持轨道!")if not valid_e:st.sidebar.warning(f"逃逸器初始位置或速度不合理，可能无法维持轨道!")# 创建航天器实例pursuer = Spacecraft(case["p_pos"], case["p_vel"], case["p_thrust"], case["p_name"])evader = Spacecraft(case["e_pos"], case["e_vel"], case["e_thrust"], case["e_name"])tbp = TwoBodyProblem(pursuer, evader)# 解算器参数max_time = st.sidebar.number_input("最大仿真时间 (分钟)", min_value=0.1, max_value=1000.0, value=60.0) * MIN2SECsim_method = st.sidebar.selectbox("仿真方法", ["标准动力学", "简化控制策略"])min_altitude = st.sidebar.number_input("最低飞行高度 (km)", min_value=100.0, max_value=GEO_ALTITUDE, value=100.0)create_animation_flag = st.sidebar.checkbox("生成轨迹动画", value=False)interactive_plot = st.sidebar.checkbox("交互式3D轨迹图", value=True)# 运行仿真if st.button("开始仿真"):st.header("仿真结果")with st.spinner('正在进行轨道计算...'):t0 = time.time()if sim_method == "标准动力学":# 标准动力学仿真t_span = [0, max_time]solution = solve_ivp(tbp.dynamics,t_span,tbp.states,method='DOP853',rtol=rtol,atol=atol,dense_output=True)t = solution.tstates = solution.yelif sim_method == "简化控制策略":# 使用简化控制策略pursuer_ctrl = SimpleControlSolver(pursuer, is_pursuer=True)evader_ctrl = SimpleControlSolver(evader, is_pursuer=False)# 时间步进 - 自适应步长step = 1.0  # 初始时间步长(秒)t = [0]states = np.zeros((12, 1))states[:, 0] = tbp.statesi = 0current_time = 0while current_time < max_time and i < 100000:  # 最大迭代次数保护# 更新控制pursuer_ctrl.update(evader.state, step)evader_ctrl.update(pursuer.state, step)# 积分一步dy = tbp.dynamics(current_time, states[:, i]) * stepnew_state = states[:, i] + dy# 检查是否发生碰撞if np.linalg.norm(new_state[:3] - new_state[6:9]) < 0.1:tbp.status = "航天器碰撞!"states = np.hstack([states, new_state.reshape(12, 1)])t.append(current_time + step)break# 检查是否到达地球表面if np.linalg.norm(new_state[:3]) <= RE or np.linalg.norm(new_state[6:9]) <= RE:states = np.hstack([states, new_state.reshape(12, 1)])t.append(current_time + step)break# 更新状态states = np.hstack([states, new_state.reshape(12, 1)])pursuer.update_state(new_state[:6])evader.update_state(new_state[6:])current_time += stept.append(current_time)i += 1# 自适应步长调整relative_dist = np.linalg.norm(pursuer.r - evader.r)if relative_dist < 100:  # 当距离小于100km时减小步长step = max(0.1, step * 0.9)elif relative_dist > 1000:  # 当距离大于1000km时增加步长step = min(5.0, step * 1.1)# 转换为与标准动力学相同的格式solution = type('obj', (object,), {'t': np.array(t), 'y': states})t = solution.t# 更新状态历史for i in range(len(t)):if i < states.shape[1]:pursuer.update_state(states[:6, i])evader.update_state(states[6:12, i])simulation_time = time.time() - t0tbp.simulation_time = simulation_timest.success(f"轨道计算完成! 耗时: {simulation_time:.2f}秒")# 检查仿真状态if tbp.status != "尚未运行" and tbp.status != "航天器碰撞!":st.warning(tbp.status)# 显示结果st.subheader("终端状态")col1, col2 = st.columns(2)with col1:st.markdown(f"**{pursuer.name}**")st.markdown(f"- 位置: ({states[0, -1]:.2f}, {states[1, -1]:.2f}, {states[2, -1]:.2f}) km")st.markdown(f"- 速度: ({states[3, -1]:.4f}, {states[4, -1]:.4f}, {states[5, -1]:.4f}) km/s")st.markdown(f"- 高度: {pursuer.get_altitude():.2f} km")st.markdown(f"- 速度大小: {pursuer.get_speed():.4f} km/s")st.markdown(f"**轨道根数**")if pursuer.orbital_elements:st.markdown(f"- 半长轴: {pursuer.orbital_elements['a']:.2f} km")st.markdown(f"- 离心率: {pursuer.orbital_elements['e']:.4f}")st.markdown(f"- 轨道倾角: {pursuer.orbital_elements['i']:.2f}°")st.markdown(f"- 轨道周期: {pursuer.get_orbital_period():.2f} 分钟")with col2:st.markdown(f"**{evader.name}**")st.markdown(f"- 位置: ({states[6, -1]:.2f}, {states[7, -1]:.2f}, {states[8, -1]:.2f}) km")st.markdown(f"- 速度: ({states[9, -1]:.4f}, {states[10, -1]:.4f}, {states[11, -1]:.4f}) km/s")st.markdown(f"- 高度: {evader.get_altitude():.2f} km")st.markdown(f"- 速度大小: {evader.get_speed():.4f} km/s")st.markdown(f"**轨道根数**")if evader.orbital_elements:st.markdown(f"- 半长轴: {evader.orbital_elements['a']:.2f} km")st.markdown(f"- 离心率: {evader.orbital_elements['e']:.4f}")st.markdown(f"- 轨道倾角: {evader.orbital_elements['i']:.2f}°")st.markdown(f"- 轨道周期: {evader.get_orbital_period():.2f} 分钟")r_p = states[:3, -1]r_e = states[6:9, -1]terminal_dist = np.linalg.norm(r_p - r_e)st.markdown(f"**终端相对距离**: {terminal_dist:.2f} km")st.markdown(f"**仿真时间**: {t[-1] / 60:.2f} 分钟")# 3D轨迹图st.subheader("轨道轨迹")if interactive_plot:# 使用Plotly创建交互式3D轨迹图fig = plot_interactive_3d(t, states, pursuer.name, evader.name)st.plotly_chart(fig, use_container_width=True)else:# 使用Matplotlib创建静态3D轨迹图fig = plot_3d_trajectory(t, states, pursuer.name, evader.name)st.pyplot(fig)# 距离变化曲线st.subheader("相对距离变化")distances = []for i in range(states.shape[1]):r_p = states[:3, i]r_e = states[6:9, i]distances.append(np.linalg.norm(r_p - r_e))plt.figure(figsize=(10, 4))plt.plot(np.array(t) / MIN2SEC, distances, 'b-')plt.axhline(y=0.1, color='r', linestyle='--', alpha=0.5, label="碰撞临界")plt.xlabel('时间 (分钟)')plt.ylabel('相对距离 (km)')plt.title('追逃航天器相对距离变化')plt.grid(True)plt.legend()st.pyplot(plt)# 高度变化曲线st.subheader("轨道高度变化")heights_p = []heights_e = []for i in range(states.shape[1]):r_p = states[:3, i]r_e = states[6:9, i]heights_p.append(np.linalg.norm(r_p) - RE)heights_e.append(np.linalg.norm(r_e) - RE)plt.figure(figsize=(10, 4))plt.plot(np.array(t) / MIN2SEC, heights_p, 'g-', label=pursuer.name)plt.plot(np.array(t) / MIN2SEC, heights_e, 'r-', label=evader.name)plt.axhline(y=min_altitude, color='gray', linestyle='--', label='最低高度限制')plt.axhline(y=GEO_ALTITUDE, color='b', linestyle='-.', label='地球静止轨道', alpha=0.5)plt.xlabel('时间 (分钟)')plt.ylabel('高度 (km)')plt.title('航天器轨道高度变化')plt.legend()plt.grid(True)st.pyplot(plt)# 显示控制力历史if hasattr(pursuer, 'control_history') and len(pursuer.control_history) > 0:st.subheader("控制力分析")u_p = np.array(pursuer.control_history)u_e = np.array(evader.control_history)# 确保时间点与控制点数量一致t_p = np.array(pursuer.time_history)t_e = np.array(evader.time_history)# 控制力大小plt.figure(figsize=(10, 6))plt.subplot(211)# 确保维度匹配if len(t_p) == len(u_p):plt.plot(t_p / MIN2SEC, np.linalg.norm(u_p, axis=1), 'g-', label='追踪器推力')# 显示推力消耗thrust_consumption_p = np.trapz(np.linalg.norm(u_p, axis=1), t_p)plt.text(0.7, 0.9, f"总推力消耗: {thrust_consumption_p:.4f} km/s²·s",transform=plt.gca().transAxes, fontsize=9)else:st.warning(f"追踪器控制点({len(u_p)})与时间点({len(t_p)})数量不匹配")if len(t_e) == len(u_e):plt.plot(t_e / MIN2SEC, np.linalg.norm(u_e, axis=1), 'r-', label='逃逸器推力')thrust_consumption_e = np.trapz(np.linalg.norm(u_e, axis=1), t_e)plt.text(0.7, 0.8, f"总推力消耗: {thrust_consumption_e:.4f} km/s²·s",transform=plt.gca().transAxes, fontsize=9)else:st.warning(f"逃逸器控制点({len(u_e)})与时间点({len(t_e)})数量不匹配")plt.xlabel('时间 (分钟)')plt.ylabel('推力大小 (km/s²)')plt.title('推力变化')plt.legend()plt.grid(True)# 推力方向角plt.subplot(212)if len(t_p) == len(u_p):azimuth_p = np.arctan2(u_p[:, 1], u_p[:, 0]) * 180 / np.pielevation_p = np.arctan2(u_p[:, 2], np.sqrt(u_p[:, 0] ** 2 + u_p[:, 1] ** 2)) * 180 / np.piplt.plot(t_p / MIN2SEC, azimuth_p, 'g-', label='追踪器方位角')plt.plot(t_p / MIN2SEC, elevation_p, 'g--', label='追踪器俯仰角')if len(t_e) == len(u_e):azimuth_e = np.arctan2(u_e[:, 1], u_e[:, 0]) * 180 / np.pielevation_e = np.arctan2(u_e[:, 2], np.sqrt(u_e[:, 0] ** 2 + u_e[:, 1] ** 2)) * 180 / np.piplt.plot(t_e / MIN2SEC, azimuth_e, 'r-', label='逃逸器方位角')plt.plot(t_e / MIN2SEC, elevation_e, 'r--', label='逃逸器俯仰角')plt.xlabel('时间 (分钟)')plt.ylabel('角度 (度)')plt.title('推力方向角')plt.legend()plt.grid(True)plt.tight_layout()st.pyplot(plt)# 导出控制数据if st.checkbox("导出控制数据"):df_control = pd.DataFrame({'time': t_p / MIN2SEC,'p_u_x': u_p[:, 0],'p_u_y': u_p[:, 1],'p_u_z': u_p[:, 2],'p_u_mag': np.linalg.norm(u_p, axis=1),'e_u_x': u_e[:, 0],'e_u_y': u_e[:, 1],'e_u_z': u_e[:, 2],'e_u_mag': np.linalg.norm(u_e, axis=1)})csv = df_control.to_csv(index=False).encode('utf-8')st.download_button(label="下载控制数据 (CSV)",data=csv,file_name="control_data.csv",mime="text/csv")# 生成轨迹动画if create_animation_flag and tbp.status == "尚未运行":with st.spinner('生成轨迹动画中...'):anim = create_animation(t, states, pursuer.name, evader.name)# 创建临时文件保存动画with tempfile.NamedTemporaryFile(suffix=".gif", delete=False) as tmpfile:anim.save(tmpfile.name, writer='pillow', fps=20)tmpfile_path = tmpfile.name# 读取临时文件内容with open(tmpfile_path, 'rb') as f:gif_data = f.read()# 删除临时文件os.unlink(tmpfile_path)st.subheader("轨迹动画")st.image(gif_data, caption="航天器追逃轨迹动画")# 提供下载链接st.download_button(label="下载轨迹动画",data=gif_data,file_name="spacecraft_animation.gif",mime="image/gif")# 导出完整数据st.subheader("数据导出")if st.checkbox("导出完整仿真数据"):df = pd.DataFrame({'time': t,'p_x': states[0, :],'p_y': states[1, :],'p_z': states[2, :],'p_vx': states[3, :],'p_vy': states[4, :],'p_vz': states[5, :],'e_x': states[6, :],'e_y': states[7, :],'e_z': states[8, :],'e_vx': states[9, :],'e_vy': states[10, :],'e_vz': states[11, :],'distance': distances})csv = df.to_csv(index=False).encode('utf-8')st.download_button(label="下载完整仿真数据 (CSV)",data=csv,file_name="simulation_data.csv",mime="text/csv")# 算法说明st.header("算法说明")st.markdown("""### 基于同伦方法的鞍点解求解算法1. **问题建模**- 考虑J2摄动的轨道动力学- 终端拦截约束：$\\| r_p(t_f) - r_e(t_f) \\| = 0$- 最小时间目标函数：$J = t_f$2. **辅助问题求解**- 逃逸器不机动的时间最优拦截问题- 使用数值优化求解终端时间和初始协态量- 通过简化实现展示核心流程3. **同伦过程**将逃逸器的推力加速度作为同伦参数，从0（辅助问题）逐渐增加到设定值（原问题），通过连续过渡求解鞍点解。### J2摄动项计算摄动加速度公式：$$\\begin{align*}a_{J2,x} &= \\frac{3J_2\\mu R_E^2}{2r^5} \\left(5\\frac{z^2}{r^2} - 1\\right) x \\\\a_{J2,y} &= \\frac{3J_2\\mu R_E^2}{2r^5} \\left(5\\frac{z^2}{r^2} - 1\\right) y \\\\a_{J2,z} &= \\frac{3J_2\\mu R_E^2}{2r^5} \\left(5\\frac{z^2}{r^2} - 3\\right) z\\end{align*}$$其中：- $\\mu$: 地球引力常数- $J_2$: J2摄动系数- $R_E$: 地球赤道半径- $r = \\sqrt{x^2 + y^2 + z^2}$: 航天器位置矢量模长### 主要增强功能：1. **轨道根数计算**：实时计算和显示航天器的轨道参数2. **轨迹动画**：生成动态演示航天器运动的动画3. **数据导出**：支持导出仿真数据和控制数据4. **性能优化**：添加精度选项和自适应步长控制5. **参数验证**：检查初始状态是否合理6. **增强可视化**：添加地球静止轨道线并改进地球渲染7. **碰撞检测**：增加航天器碰撞和坠毁检测8. **交互式3D轨迹图**：使用Plotly实现可交互的3D轨迹可视化""")if __name__ == "__main__":main()
查看全文
http://www.lryc.cn/news/608567.html