当前位置：首页 > news >正文

【问题思考总结】CART树如何剪枝？从CART树的生成到剪枝以及为什么CTt一定小于Ct？【图文】

news 2025/8/2 11:34:11

问题

今天在看统计学习方法中的CART剪枝部分时，感觉有很多不懂得地方，貌似是从之前决策树得生成开始积攒的问题攒到现在了，于是准备在这里好好梳理一下。

我的问题主要就是：
为什么这里CTt一定小于Ct？也就是说，为什么子结点没有子树的总基尼指数小？

思考

我想，首先要从决策树的生成开始想起，在最开始，决策树从根节点向下构建，有一个很重要的因素就是（也是我之前忽略的，我没证明过），决策树在构建的过程中，每次结点的分裂都指向基尼系数的减少。 也就是说，每次分裂出一个新的子树，基尼系数都会减小，最后生成的树就是基尼系数最小的树。

那么，因为我现在的树是基尼系数最小的树，于是，不管是剪去任意一个结点，我一定基尼系数是比之前要更大的（原因很简单，他们都是一步一步生成的，而每一次生成都是减少基尼指数的过程。

由此，就可以解决我们之前的问题，为什么CTt一定小于Ct？

至此，完成一大步，之后就好办了。

p.s 我认为很可能是搞混了Gini（D）和Gini（D，A）（因为后者在树上是等于两个子树的基尼系数，我就有点懵懵的。。。）

然后我又想到，万一Gini（D）小于后面这一项怎么办，但是查询得基于凸函数的性质，不会有问题。。。看来还是要多看看数学啊！真累！保持学术的纯粹性真累！我也25了，纯粹的求知还能有多久？希望可以永葆初心！至少在求真这方面，不要变，是什么就是什么，学术马虎不得！
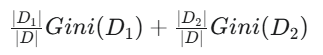
在这里插入图片描述

总结

我想的太多了，总的来说！这里生成算法和剪枝算法都是一样的，生成的时候是一个基尼系数递减的过程，剪枝的时候是基尼系数递增的过程，但是因为有了α的存在，针对于不同的α，生成的树是不同的，对应了不同的对模型复杂度的重视程度。我现在知道的大概就是这些！

我觉得这样的说法是大概正确的，在我的认知里，如果里面哪里有错误，恳请不吝赐教！另外，这里也都是没有严格证明的，只是看结果似乎是这样的，经过大模型和观看自己视频的自己的思考，希望能给大家提供一些灵感，有一些帮助，将是我心甚慰，这也是做这个博客一直以来的初衷，希望能发现真实的问题，并且解决问题，帮到像我一样认真求索的人，真心话！希望能帮人帮己，真心相对。说多了！如果哪里有不对的地方恳请指正！共同进步！干就完了！