leetcode热题——螺旋矩阵

目录

螺旋矩阵

题目描述

题解

方法一：边界收缩法

核心思想

算法步骤

C++ 代码实现

复杂度分析

方法二：方向向量法

核心思想

算法步骤

C++ 代码实现

复杂度分析

方法三：递归法

核心思想

C++ 代码实现

复杂度分析

方法四：层次遍历法

核心思想

C++ 代码实现

复杂度分析

螺旋矩阵四种方法全面对比总结

方法概览对比

详细分析对比

1. 边界收缩法 ⭐⭐⭐⭐⭐ (最推荐)

核心思想

优势

劣势

适用场景

2. 方向向量法 ⭐⭐⭐ (学习友好)

核心思想

优势

劣势

适用场景

3. 递归法 ⭐⭐ (思维训练)

核心思想

优势

劣势

适用场景

4. 层次遍历法 ⭐⭐⭐⭐ (工程实用)

核心思想

优势

劣势

适用场景

面试策略建议

一面/基础面试

二面/深度面试

算法专场面试

学习路径建议

阶段1：理解螺旋遍历本质

阶段2：掌握标准解法

阶段3：拓展算法思维

实际开发建议

生产环境首选

学习和教学首选

算法面试首选

大数据处理

---

螺旋矩阵

题目描述

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

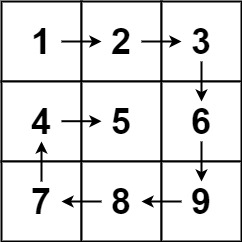
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

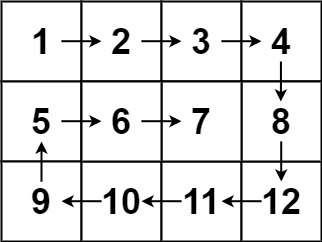
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示： m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

题解

方法一：边界收缩法

核心思想

维护四个边界：上、下、左、右，按照螺旋顺序遍历后逐步收缩边界。

算法步骤

(1)向右：从左边界到右边界，遍历上边界行
(2)向下：从上边界到下边界，遍历右边界列
(3)向左：从右边界到左边界，遍历下边界行
(4)向上：从下边界到上边界，遍历左边界列
(5)每次遍历完一个方向后，相应收缩边界

C++ 代码实现

#include <vector>
using namespace std;class Solution {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {if (matrix.empty() || matrix[0].empty()) {return {};}int m = matrix.size(), n = matrix[0].size();vector<int> result;// 定义四个边界int top = 0, bottom = m - 1;int left = 0, right = n - 1;while (top <= bottom && left <= right) {// 1. 向右遍历上边界for (int col = left; col <= right; col++) {result.push_back(matrix[top][col]);}top++;  // 上边界下移// 2. 向下遍历右边界for (int row = top; row <= bottom; row++) {result.push_back(matrix[row][right]);}right--;  // 右边界左移// 3. 向左遍历下边界（如果还有行）if (top <= bottom) {for (int col = right; col >= left; col--) {result.push_back(matrix[bottom][col]);}bottom--;  // 下边界上移}// 4. 向上遍历左边界（如果还有列）if (left <= right) {for (int row = bottom; row >= top; row--) {result.push_back(matrix[row][left]);}left++;  // 左边界右移}}return result;}
};

复杂度分析

时间复杂度： O(m×n)
空间复杂度： O(1)（不计算结果数组）

方法二：方向向量法

核心思想

使用方向向量控制移动方向，遇到边界或已访问元素时转向。

算法步骤

(1)定义四个方向：右、下、左、上
(2)使用visited数组标记已访问元素
(3)当前方向无法继续时，按顺时针转向

C++ 代码实现

#include <vector>
using namespace std;class Solution {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {if (matrix.empty() || matrix[0].empty()) {return {};}int m = matrix.size(), n = matrix[0].size();vector<vector<bool>> visited(m, vector<bool>(n, false));vector<int> result;// 方向向量：右、下、左、上vector<pair<int, int>> directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};int direction_idx = 0;int row = 0, col = 0;for (int i = 0; i < m * n; i++) {result.push_back(matrix[row][col]);visited[row][col] = true;// 计算下一个位置int dr = directions[direction_idx].first;int dc = directions[direction_idx].second;int next_row = row + dr;int next_col = col + dc;// 检查是否需要转向if (next_row < 0 || next_row >= m || next_col < 0 || next_col >= n || visited[next_row][next_col]) {// 转向direction_idx = (direction_idx + 1) % 4;dr = directions[direction_idx].first;dc = directions[direction_idx].second;next_row = row + dr;next_col = col + dc;}row = next_row;col = next_col;}return result;}
};

复杂度分析

时间复杂度： O(m×n)
空间复杂度： O(m×n)（visited数组）

方法三：递归法

核心思想

递归法的核心思想是分层处理：

(1)处理最外层的一圈元素
(2)递归处理内层子矩阵
(2)将结果合并

这种方法将复杂的螺旋遍历问题分解为：外圈遍历 + 内圈递归

C++ 代码实现

#include <vector>
using namespace std;class Solution {
private:// 递归函数：处理指定边界内的螺旋遍历vector<int> spiral_recursive(vector<vector<int>>& matrix, int top, int bottom, int left, int right) {// 递归终止条件：无效边界if (top > bottom || left > right) {return {};}vector<int> result;// 特殊情况1：只有一行if (top == bottom) {for (int col = left; col <= right; col++) {result.push_back(matrix[top][col]);}return result;}// 特殊情况2：只有一列if (left == right) {for (int row = top; row <= bottom; row++) {result.push_back(matrix[row][left]);}return result;}// 一般情况：遍历完整的外圈// 1. 上边界：从左到右（不包括右上角，避免重复）for (int col = left; col < right; col++) {result.push_back(matrix[top][col]);}// 2. 右边界：从上到下（不包括右下角，避免重复）for (int row = top; row < bottom; row++) {result.push_back(matrix[row][right]);}// 3. 下边界：从右到左（不包括左下角，避免重复）for (int col = right; col > left; col--) {result.push_back(matrix[bottom][col]);}// 4. 左边界：从下到上（不包括左上角，避免重复）for (int row = bottom; row > top; row--) {result.push_back(matrix[row][left]);}// 递归处理内圈：边界各缩小1vector<int> inner = spiral_recursive(matrix, top + 1, bottom - 1, left + 1, right - 1);// 合并外圈和内圈结果result.insert(result.end(), inner.begin(), inner.end());return result;}public:vector<int> spiralOrder(vector<vector<int>>& matrix) {if (matrix.empty() || matrix[0].empty()) {return {};}int m = matrix.size(), n = matrix[0].size();return spiral_recursive(matrix, 0, m - 1, 0, n - 1);}
};

复杂度分析

时间复杂度：O(m×n)
每个元素只被访问一次 递归层数最多为 min(m,n)/2 总的元素访问次数为 m×n

空间复杂度：O(min(m,n))
递归栈深度为矩阵的层数：⌈min(m,n)/2⌉ 每层递归需要常数空间 不计算结果数组的话，空间复杂度为递归栈的深度

方法四：层次遍历法

核心思想

将矩阵看作多个同心矩形层，从外层到内层逐层遍历。

C++ 代码实现

#include <vector>
#include <algorithm>
using namespace std;class Solution {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {if (matrix.empty() || matrix[0].empty()) {return {};}int m = matrix.size(), n = matrix[0].size();vector<int> result;// 计算层数int layers = (min(m, n) + 1) / 2;for (int layer = 0; layer < layers; layer++) {// 当前层的边界int top = layer, bottom = m - 1 - layer;int left = layer, right = n - 1 - layer;if (top > bottom || left > right) {break;}// 特殊情况：只有一行或一列if (top == bottom) {for (int col = left; col <= right; col++) {result.push_back(matrix[top][col]);}} else if (left == right) {for (int row = top; row <= bottom; row++) {result.push_back(matrix[row][left]);}} else {// 正常的一圈// 上边界for (int col = left; col < right; col++) {result.push_back(matrix[top][col]);}// 右边界for (int row = top; row < bottom; row++) {result.push_back(matrix[row][right]);}// 下边界for (int col = right; col > left; col--) {result.push_back(matrix[bottom][col]);}// 左边界for (int row = bottom; row > top; row--) {result.push_back(matrix[row][left]);}}}return result;}
};

复杂度分析

时间复杂度： O(m×n)
空间复杂度： O(1)（不计算结果数组）

螺旋矩阵四种方法全面对比总结

方法概览对比

方法	时间复杂度	空间复杂度	核心思想	难度	推荐度
边界收缩法	O(m×n)	O(1)	维护四个边界，逐步收缩	⭐⭐⭐	⭐⭐⭐⭐⭐
方向向量法	O(m×n)	O(m×n)	模拟移动，遇障碍转向	⭐⭐	⭐⭐⭐
递归法	O(m×n)	O(min(m,n))	外圈+内圈分层处理	⭐⭐⭐⭐	⭐⭐
层次遍历法	O(m×n)	O(1)	按层遍历，从外到内	⭐⭐⭐	⭐⭐⭐⭐

---

详细分析对比

1. 边界收缩法 ⭐⭐⭐⭐⭐ (最推荐)

核心思想

维护四个边界：top, bottom, left, right
按螺旋方向遍历：右→下→左→上
每完成一个方向，收缩对应边界

优势

• ✅ 空间效率最高：O(1)空间复杂度
• ✅ 逻辑直观：边界概念清晰易懂
• ✅ 代码简洁：循环结构简单
• ✅ 面试标准解法：被广泛认可

劣势

• ❌ 边界条件复杂：需要仔细处理边界收缩时机
• ❌ 调试稍难：边界错误不易发现

适用场景

• 面试首选方案
• 对空间要求严格的场景
• 需要高效稳定解法的生产环境

// 关键代码片段
while (top <= bottom && left <= right) {// 右→下→左→上，每次遍历后收缩边界for (int col = left; col <= right; col++) result.push_back(matrix[top][col]);top++;// ... 其他三个方向
}

---

2. 方向向量法 ⭐⭐⭐ (学习友好)

核心思想

定义方向向量：{右, 下, 左, 上}
模拟螺旋移动，遇到边界或已访问元素时转向
使用visited数组标记访问状态

优势

• ✅ 最易理解：直接模拟螺旋移动过程
• ✅ 逻辑自然：符合人类思维方式
• ✅ 易于扩展：可以轻松改变移动方向
• ✅ 调试友好：每步移动都清晰可见

劣势

• ❌ 空间开销大：需要O(m×n)的visited数组
• ❌ 性能略差：每步都要检查多个条件

适用场景

• 学习算法时的理解工具
• 需要可视化过程的场景
• 对空间要求不严格的情况

// 关键代码片段
vector<pair<int, int>> directions = {{0,1}, {1,0}, {0,-1}, {-1,0}};
// 检查转向条件：越界或已访问
if (next_row < 0 || next_row >= m || visited[next_row][next_col]) {direction_idx = (direction_idx + 1) % 4;
}

---

3. 递归法 ⭐⭐ (思维训练)

核心思想

分治思想：外圈遍历 + 内圈递归
递归处理每一层，最终合并结果
边界参数：top, bottom, left, right

优势

• ✅ 思路最清晰：分层思维符合人类直觉
• ✅ 代码结构好：递归天然的分解结构
• ✅ 易于理解：问题分解明确
• ✅ 展示算法思维：体现分治思想

劣势

• ❌ 空间开销：递归栈深度O(min(m,n))
• ❌ 性能开销：函数调用成本
• ❌ 栈溢出风险：大矩阵可能导致栈溢出
• ❌ 复杂边界处理：需要处理单行单列情况

适用场景

• 算法思维训练
• 面试中展示分治思想
• 小规模数据处理

// 关键代码片段
vector<int> spiral_recursive(matrix, top, bottom, left, right) {// 处理外圈 + 递归内圈// 外圈：上→右→下→左// 递归：spiral_recursive(top+1, bottom-1, left+1, right-1)
}

---

4. 层次遍历法 ⭐⭐⭐⭐ (工程实用)

核心思想

将矩阵看作多个同心矩形层
计算总层数：(min(m,n) + 1) / 2
从外层到内层逐层遍历

优势

• ✅ 空间效率高：O(1)空间复杂度
• ✅ 思路清晰：层次概念明确
• ✅ 易于优化：可以并行处理不同层
• ✅ 工程友好：代码结构规整

劣势

• ❌ 代码稍复杂：需要处理多种边界情况
• ❌ 层数计算：需要正确理解层数概念

适用场景

• 工程项目中的实现
• 需要处理大规模矩阵的场景
• 对代码结构有要求的项目

// 关键代码片段
int layers = (min(m, n) + 1) / 2;
for (int layer = 0; layer < layers; layer++) {// 计算当前层边界// 处理特殊情况：单行或单列// 遍历完整一圈
}

---

面试策略建议

一面/基础面试

推荐：边界收缩法

• 先说思路，再写代码
• 重点展示边界处理能力
• 时间复杂度和空间复杂度分析

二面/深度面试

推荐：边界收缩法 + 其他方法对比

• 主要实现边界收缩法
• 简述其他方法的优劣
• 展示算法设计思维

算法专场面试

推荐：多方法展示

• 快速实现边界收缩法
• 详细解释递归法思路
• 分析各方法的适用场景

---

学习路径建议

阶段1：理解螺旋遍历本质

1. 先学方向向量法 - 最直观易懂
2. 手工模拟几个小例子
3. 理解螺旋移动的规律

阶段2：掌握标准解法

1. 重点学习边界收缩法
2. 练习边界条件处理
3. 熟练写出bug-free代码

阶段3：拓展算法思维

1. 学习递归法 - 培养分治思维
2. 理解层次遍历法 - 工程思维
3. 对比各方法优劣

---

实际开发建议

生产环境首选

边界收缩法 - 空间效率高，性能稳定

学习和教学首选

方向向量法 - 最容易理解和实现

算法面试首选

边界收缩法 + 能够解释其他方法

大数据处理

层次遍历法 - 结构清晰，易于优化