堆的理论知识

1 引入

1.1 普通二叉树不适合用数组存储的原因

普通二叉树的结构是 “不规则” 的 —— 节点的左右孩子可能缺失，且缺失位置无规律。
若用数组存储（按 “层次遍历顺序” 分配索引，即根节点放索引 0，根的左孩子放 1、右孩子放 2，以此类推），缺失的节点会导致数组中出现大量空位置，造成空间浪费。

例如：一棵只有 “右孩子” 的二叉树（根→右→右→...），按数组存储时，所有左孩子的位置（索引 1、3、7...）都会空着，这些空位置就是无效浪费。

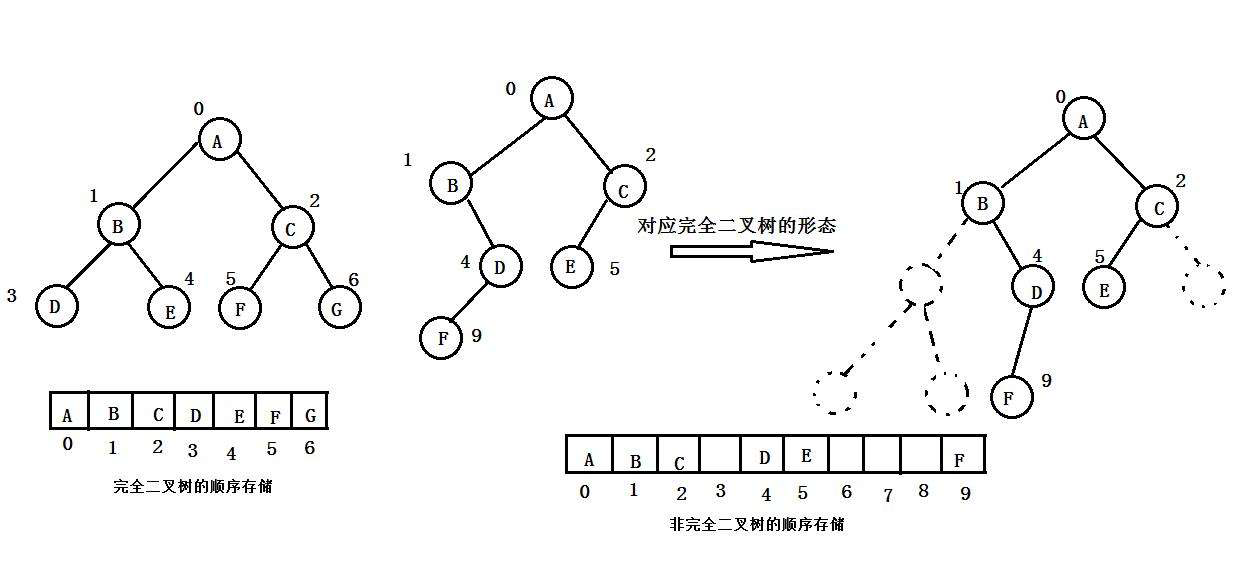
1.2 完全二叉树适合顺序存储的原因

完全二叉树的结构是 “紧凑” 的：

• 除最后一层外，其他层的节点均 “满”（即每个节点都有左右孩子）；
• 最后一层的节点从左到右 “连续排列”，没有中间缺失。

这种结构使得按层次遍历顺序存储时，数组的索引与节点位置完全对应，几乎没有空位置。例如：一个高度为 3 的完全二叉树（共 7 个节点），数组索引 0-6 会被完全填满，无任何浪费。

1.3 堆用数组存储的合理性

堆是一种 “特殊的完全二叉树”（满足 “大顶堆” 或 “小顶堆” 特性：大顶堆中每个父节点的值≥子节点，小顶堆则≤）。

由于堆本质是完全二叉树，自然继承了 “紧凑结构” 的特点，因此适合用数组存储。

数组存储堆时，通过索引可快速定位节点的父 / 子节点，规则为（假设节点在数组中索引为i）：

• 左孩子索引：2i + 1；
• 右孩子索引：2i + 2；
• 父节点索引：(i - 1) // 2（整数除法）。

这种对应关系让堆的核心操作（如 “堆化”“插入”“删除”）能通过数组索引高效实现，无需额外存储指针，既省空间又提效。

1.4. “数据结构的堆” 与 “操作系统的堆” 的区分

两者仅名称相同，本质完全无关：

• 数据结构的堆：是一种特殊的完全二叉树，用于实现优先队列（如任务调度中的 “最高优先级先执行”），核心特性是 “父节点与子节点的大小关系固定”（大顶 / 小顶）。
• 操作系统的堆：是内存中的一块区域（与 “栈” 相对），用于 “动态内存分配”（如 C 语言malloc、Javanew申请的内存均来自这里），由操作系统的内存管理模块负责分配与回收。

所以，综上所述：

堆是一种特殊的完全二叉树（满足大顶堆或小顶堆特性），而它的实现依赖于 “顺序存储”（数组）—— 这与二叉树的存储特性直接相关。

普通二叉树因结构不规则，用数组存储会产生大量空位置（例如仅右孩子存在时，左孩子的索引全为空），空间效率极低；但完全二叉树不同，其节点按层次紧凑排列，无无规律缺失，用数组存储时索引可与节点位置一一对应，几乎无空间浪费。

堆作为完全二叉树的 “特例”，天然适配数组存储：我们将堆的节点按层次遍历顺序存入数组，通过索引规则（左孩子2i+1、右孩子2i+2、父节点(i-1)//2）可快速定位任意节点的父子关系。这种存储方式让堆的核心操作能通过数组索引直接计算，无需指针，既简化实现又提升效率（时间复杂度为 O (log n)）。

需特别注意：此处的 “堆” 是数据结构概念，与操作系统中 “管理动态内存的堆区域” 完全无关 —— 前者是一种二叉树，后者是内存分段，仅名称巧合。

2 堆的概念

堆是一种特殊的完全二叉树，分为：

• 大根堆：每个节点的值≥其左右孩子的值，根最大。
• 小根堆：每个节点的值≤其左右孩子的值，根最小。

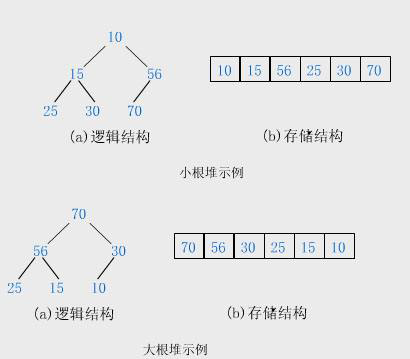
小堆不一定是升序，大堆不一定是降序，所以，成为堆并不代表有序。 

3 堆的经典选择题辨析

堆作为一种特殊的完全二叉树，其结构特性（大顶堆 / 小顶堆）和存储方式（数组顺序存储）决定了它在算法中的高频应用。本文通过 4 道经典题目，从堆的判断、删除重建、初始堆构建到调整过程，带你深入理解堆的核心逻辑。

3.1 判断下列关键字序列是否为堆

题目：下列关键字序列为堆的是（）
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32

解析：堆的核心判断标准

堆分为大顶堆（每个父节点的值≥子节点）和小顶堆（每个父节点的值≤子节点），判断序列是否为堆，需验证所有父节点与子节点的关系是否满足其一。

数组存储堆时，节点索引关系为（设节点索引为i）：

• 左孩子：2i+1，右孩子：2i+2

选项 A 分析：100,60,70,50,32,65

• 根节点（i=0）：100，左孩子（i=1）=60，右孩子（i=2）=70 → 100≥60 且 100≥70（满足大顶堆父节点要求）；
• 节点 i=1（60）：左孩子（i=3）=50，右孩子（i=4）=32 → 60≥50 且 60≥32；
• 节点 i=2（70）：左孩子（i=5）=65 → 70≥65；
  所有父节点均满足 “≥子节点”，是大顶堆。

其他选项均不满足：

• 选项 B：根节点 60 的右孩子 100＞60，不满足大顶堆；
• 选项 C：节点 i=1（100）的右孩子（i=4）=50，左孩子（i=3）=32，但根节点 65＜100，不满足大顶堆；
• 其余选项同理可证不满足堆的定义。

答案：A

3.2 小根堆删除堆顶后重建的比较次数

题目：已知小根堆为 8,15,10,21,34,16,12，删除关键字 8 之后需重建堆，比较次数是（）。
A 1 B 2 C 3 D 4

解析：小根堆的删除与重建流程

小根堆删除堆顶（最小值）的步骤：

1. 替换堆顶：用最后一个元素替换堆顶（保证结构紧凑）；
2. 向下调整：从新堆顶开始，与左右孩子中较小的节点比较，若不满足 “父≤子” 则交换，重复至平衡。

具体步骤：

原堆（数组）：[8,15,10,21,34,16,12]（长度 7，索引 0-6）

• 删除堆顶 8 后，用最后一个元素 12 替换堆顶，新数组为[12,15,10,21,34,16]（长度 6，索引 0-5）；
• 向下调整 12（堆顶）：
  • 左孩子（i=1）=15，右孩子（i=2）=10 → 较小的孩子是 10（i=2）；
  • 比较 12 与 10：12＞10，交换 → 数组变为[10,15,12,21,34,16]；
  • 调整 12（现在在 i=2）：左孩子（i=5）=16，右孩子无；
  • 比较 12 与 16：12＜16，无需交换，调整结束。

比较次数统计：

• 第一次：12 与左孩子 15、右孩子 10 比较（2 次）；
• 第二次：12 与左孩子 16 比较（1 次）；
  共 3 次比较。

答案：C

3.3 堆排序的初始堆构建

题目：一组记录排序码为 (5,11,7,2,3,17)，利用堆排序方法建立的初始堆为（）
A(11,5,7,2,3,17) B(11,5,7,2,17,3) C(17,11,7,2,3,5) D(17,11,7,5,3,2) E(17,7,11,3,5,2) F(17,7,11,3,2,5)

解析：堆排序的初始堆（大顶堆）构建

堆排序的第一步是构建大顶堆（根节点为最大值），步骤：

1. 从最后一个非叶子节点开始（索引(n-1)//2），依次向前调整；
2. 调整规则：若父节点＜子节点中较大值，则交换，并递归调整交换后的子节点。

具体步骤：

排序码：[5,11,7,2,3,17]（长度 6，索引 0-5）

• 最后一个非叶子节点索引：(6-1)//2=2（值为 7）；
  • 节点 i=2（7）的右孩子 i=5（17）→ 7＜17，交换 → 数组变为[5,11,17,2,3,7]；
• 前一个非叶子节点 i=1（11）：左孩子 i=3（2），右孩子 i=4（3）→ 11≥两者，无需调整；
• 第一个非叶子节点 i=0（5）：左孩子 i=1（11），右孩子 i=2（17）→ 5＜17，交换 → 数组变为[17,11,5,2,3,7]；
• 调整交换后 i=2（5）：右孩子 i=5（7）→ 5＜7，交换 → 数组变为[17,11,7,2,3,5]，此时所有父节点均满足大顶堆规则。

答案：C

3.4 最小堆删除堆顶后的结果

题目：最小堆 [0,3,2,5,7,4,6,8]，在删除堆顶元素 0 之后，其结果是（）
A[3，2，5，7，4，6，8] B[2，3，5，7，4，6，8] C[2，3，4，5，7，8，6] D[2，3，4，5，6，7，8]

解析：最小堆的删除与调整

最小堆删除堆顶（最小值）的流程与题目 2 一致：替换堆顶→向下调整（保证父≤子）。

具体步骤：

原堆：[0,3,2,5,7,4,6,8]（长度 8，索引 0-7）

• 删除 0 后，用最后一个元素 8 替换堆顶 → 新数组[8,3,2,5,7,4,6]（长度 7，索引 0-6）；
• 向下调整 8（堆顶）：
  • 左孩子 i=1（3），右孩子 i=2（2）→ 较小孩子是 2（i=2）；
  • 8＞2，交换 → 数组变为[2,3,8,5,7,4,6]；
• 调整 8（i=2）：
  • 左孩子 i=5（4），右孩子 i=6（6）→ 较小孩子是 4（i=5）；
  • 8＞4，交换 → 数组变为[2,3,4,5,7,8,6]；
• 8（i=5）无孩子，调整结束。

答案：C