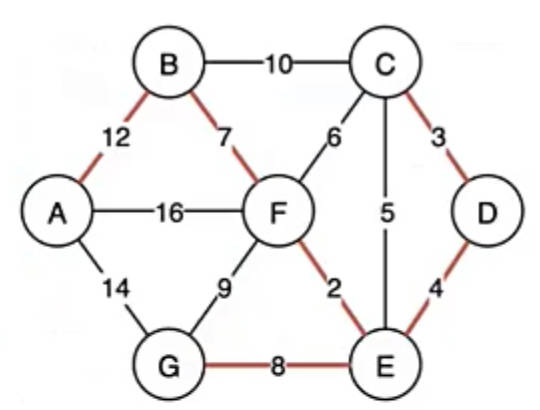
Kruskal算法

一，最小生成树

1.定义：n个顶点的的连通图取其n-1条边，构成一个最小连通子图，并使该连通子图中n-1条边上权值之和达到最小值，则称其为连通网的最小连通子图

2.生成树的属性：

a.生成树当中不存在环（环：一个顶点经过若干条边能回到本身，且经过的边不能重复）

b.对于n个顶点的无向完全图，最多包含n^n-3棵生成树

3.最小生成树

所谓带权图的最小生成树，就是原图中边的权值最小的生成树

4.Kruskal（克鲁斯卡尔）算法

逻辑：

a.总共找n-1条边，每次都找权值最小的那条边，但必须保证这条边的加入不会产生环

b.如何判断是否生成环，需要之前学过的并查集，添加一条边有两个顶点<a,b>，判断a和b是否在一个集合