当前位置：首页 > news >正文

数据结构【红黑树】

news 2025/7/30 5:58:45

红黑树

1.红黑树
- 1.1红黑树的定义
- 1.2红黑树的规则
- 1.3红黑树的效率：
2.红黑树的实现
- 2.1红黑树的插入
- - 2.1.1 情况1:变色
  - 2.1.2 情况2：单旋+变色
  - 2.1.3 情况3：双旋+变色
- 2.2红黑树的插入代码实现
- 2.3红黑树的查找
- 2.4红黑树的检查

1.红黑树

1.1红黑树的定义

红黑树是⼀棵二叉搜索树，它的每个结点增加一个存储位来表示结点的颜色，可以是红色或者黑色。
通过对任何一条从根到叶子的路径上各个结点的颜色进行约束，最长的不超过最短的2倍（近似平衡）。
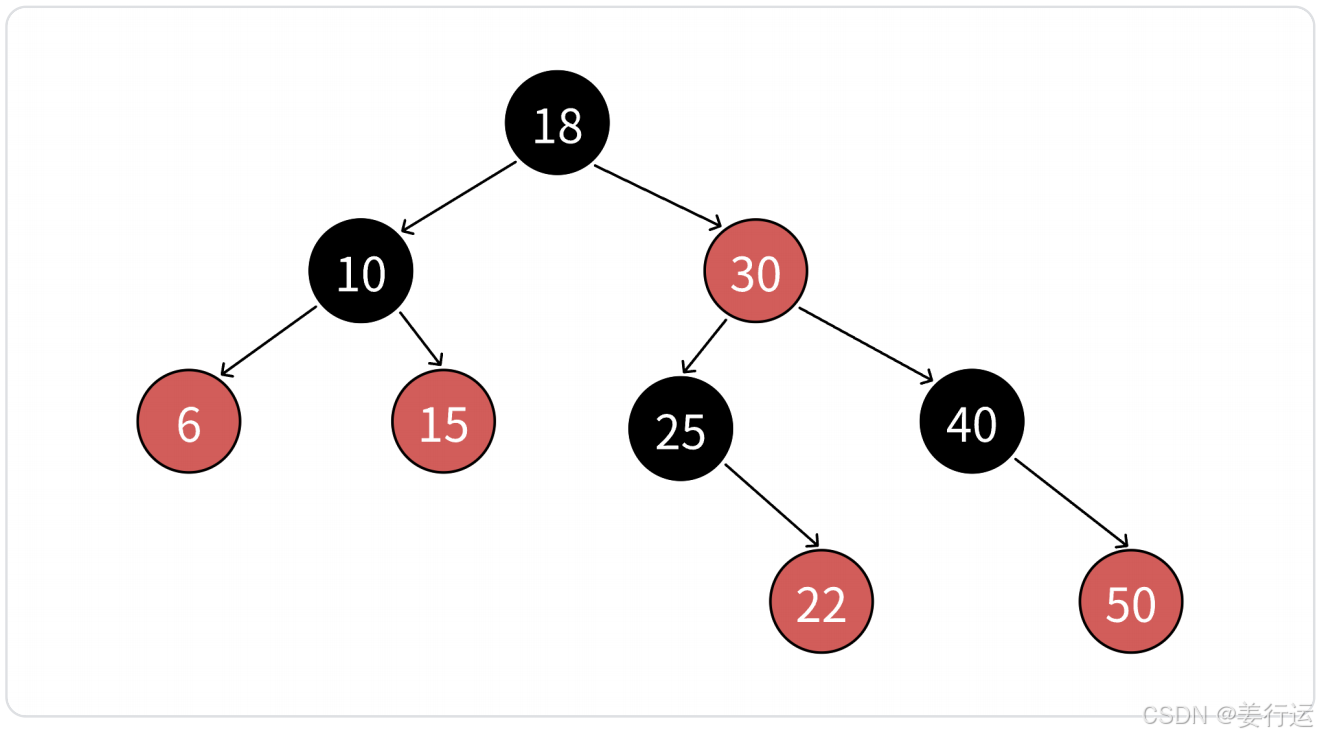
在这里插入图片描述

1.2红黑树的规则

每个结点不是红色就是黑色
根结点是黑色的
如果一个结点是红色的，则它的两个孩子结点必须是黑色的，也就是说任意一条路径不会有连续的红色结点。
对于任意一个结点，从该结点到其所有NULL结点的简单路径上，均包含相同数量的黑色结点。
最长路径（一黑一红） < = 2*最短路径（全黑）（四条规则约束）
数路径要数到空结点。（NIL结点数路径）

1.3红黑树的效率：

最短路径logN，最长路径2*logN，时间复杂度就是O(logN)。

2.红黑树的实现

2.1红黑树的插入

(插入红色结点，按照二叉搜索树的规则，和四条红黑树的规则）

2.1.1 情况1:变色

-c为红，p为红，g为黑，u存在且为红，则将p和u变黑，g变红。在把g当做新的c，继续往上更新。
情况1只变色，不旋转。所以无论c是p的左还是右，p是g的左还是右，都是上面的变色处理方式。

2.1.2 情况2：单旋+变色

c为红，p为红，g为黑，u不存在或者u存在且为黑，u不存在，则c一定是新增结点，u存在且为黑，则c一定不是新增，c之前是黑色的，是在c的子树中插入，符合情况1，变色将c从黑色变成红色，更新上来的。

2.1.3 情况3：双旋+变色

c为红，p为红，g为黑，u不存在或者u存在且为黑，u不存在，则c一定是新增结点，u存在且为黑，则c⼀定不是新增，c之前是黑色的，是在c的子树中插入，符合情况1，变色将c从黑色变成红色，更新上来的。

2.2红黑树的插入代码实现

//test.cpp
#include<iostream>
#include<vector>using namespace std;#include"RBTree.h"//void TestRBTree1()
//{
//    RBTree<int, int> t;
//    // 常规的测试用例
//    //int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
//    // 特殊的带有双旋场景的测试用例
//    int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14,3,5,66,33,543,54,2,435,321,32,43,4324,534 };
//    for (auto e : a)
//    {
//        t.Insert({ e, e });
//    }
//
//    t.InOrder();
//    cout << t.IsBalanceTree() << endl;
//}
//
//// 插入一堆随机值，测试平衡，顺便测试一下高度和性能等
//void TestRBTree2()
//{
//    const int N = 10000000;
//    vector<int> v;
//    v.reserve(N);
//    srand(time(0));
//
//    for (size_t i = 0; i < N; i++)
//    {
//        v.push_back(rand() + i);
//    }
//
//    size_t begin2 = clock();
//    RBTree<int, int> t;
//    for (auto e : v)
//    {
//        t.Insert(make_pair(e, e));
//    }
//    size_t end2 = clock();
//
//    cout << "Insert:" << end2 - begin2 << endl;
//    cout << t.IsBalanceTree() << endl;
//
//    cout << "Height:" << t.Height() << endl;
//    cout << "Size:" << t.Size() << endl;
//
//    size_t begin1 = clock();
//    // 确定在的值
//    /*for (auto e : v)
//    {
//            t.Find(e);
//    }*/
//
//    // 随机值
//    for (size_t i = 0; i < N; i++)
//    {
//        t.Find((rand() + i));
//    }
//
//    size_t end1 = clock();
//
//    cout << "Find:" << end1 - begin1 << endl;
//}#include"mymap.h"
#include"myset.h"int main()
{//TestRBTree2();bit::test_set();bit::test_map();return 0;
}

//RBTree.h
enum Colour
{RED,BLACK
};// red black
template<class T>
struct RBTreeNode
{T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Colour _col;RBTreeNode(const T& data):_data(data), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}
};template<class K, class T, class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node;
public:bool Insert(const T& data){if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return true;}KeyOfT kot;Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(cur->_data) < kot(data)){parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{return false;}}// 新插入红色节点cur = new Node(data);cur->_col = RED;if (kot(parent->_data) < kot(data)){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;// 1、u存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续往上处理cur = grandfather;parent = cur->_parent;}else  // 2、u不存在或者u存在且为黑{if (cur == parent->_left){//     g//  p     u//cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//     g//  p     u//     cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else // (parent == grandfather->_right){Node* uncle = grandfather->_left;// 1、u存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续往上处理cur = grandfather;parent = cur->_parent;}else  // 2、u不存在或者u存在且为黑{if (cur == parent->_right){//     g//  u    p //         cRotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//     g//  u     p//     cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}void InOrder(){_InOrder(_root);cout << endl;}int Height(){return _Height(_root);}int Size(){return _Size(_root);}Node* Find(const K& key){KeyOfT kot;Node* cur = _root;while (cur){if (kot(cur->_data) < key){cur = cur->_right;}else if (kot(cur->_data) > key){cur = cur->_left;}else{return cur;}}return nullptr;}private:int _Size(Node* root){return root == nullptr ? 0 :_Size(root->_left) + _Size(root->_right) + 1;}int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* ppnode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* ppnode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}}private:Node* _root = nullptr;
};