B树、B+树、红黑树区别
一、核心概念与性质对比
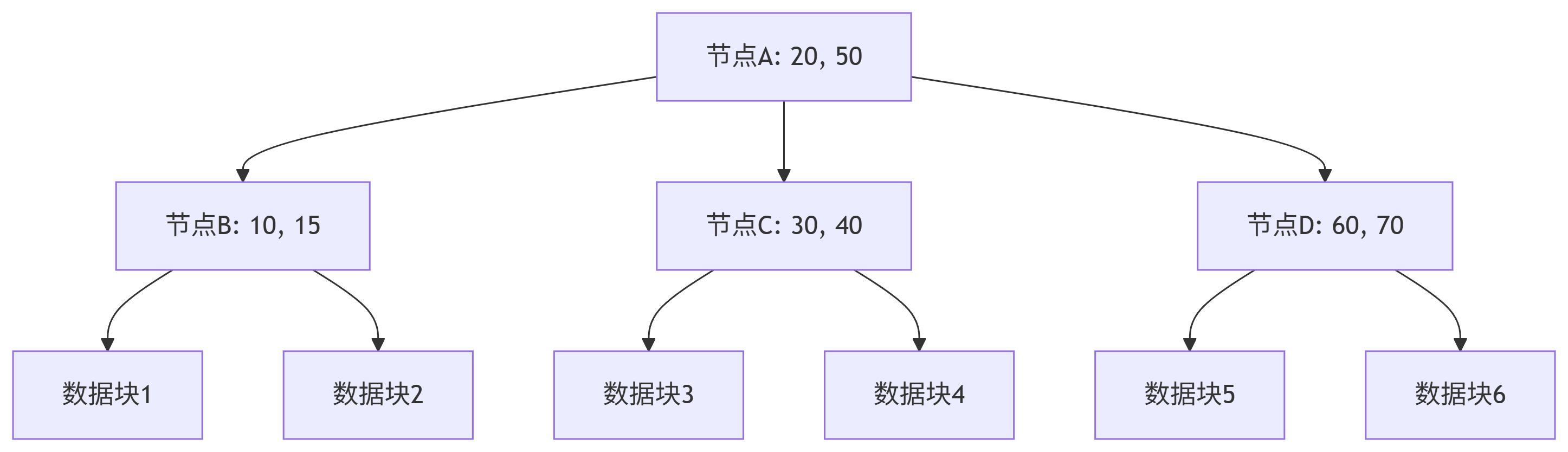
1. B树(Balanced Tree)
定位:多路平衡搜索树,专为磁盘存储优化
核心性质:
每个节点存储 k-1个键值和k个子节点指针(
m/2 ≤ k ≤ m,m为阶数)所有叶子节点位于同一层(高度平衡)
节点内键值有序排列,左子树键值均小于父节点,右子树大于父节点
优势:
减少磁盘I/O:单节点存储大量键值,树高显著降低(3-4层可存百万数据)
局部修改:插入/删除仅影响局部节点,避免全局调整1
2. B+树(B+ Tree)
定位:B树变种,数据库索引标准结构
核心性质:
非叶节点仅存键值(无数据指针),叶节点存数据并形成双向链表
非叶节点的键值在叶节点中重复出现(叶节点含所有数据)
优势:
范围查询高效:叶节点链表支持顺序遍历(如SQL的
BETWEEN)磁盘利用率更高:非叶节点容纳更多键值,进一步降低树高
查询稳定性:所有查询路径长度相同(均到叶节点)

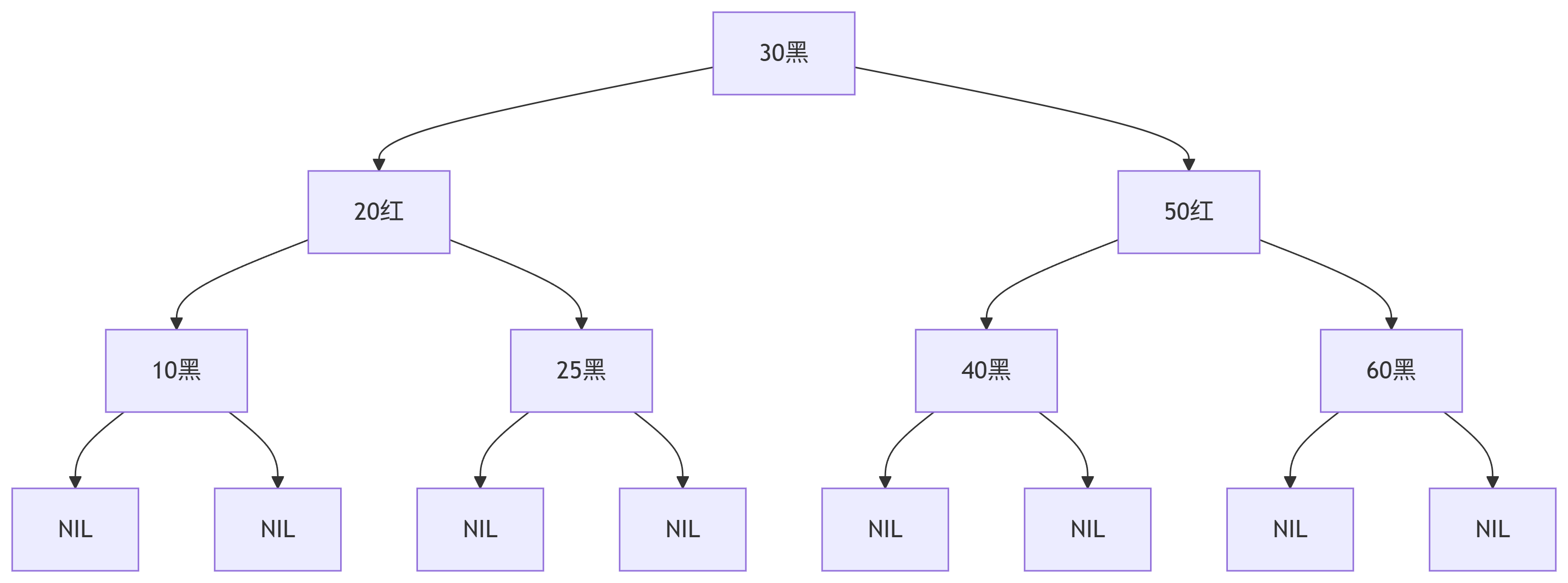
3. 红黑树(Red-Black Tree)
定位:自平衡二叉搜索树,内存操作优化
核心性质:
颜色约束:节点红/黑交替,根和叶(NIL)为黑,无连续红节点
黑高平衡:任意节点到叶节点的路径含相同黑节点数
优势:
近似平衡:最长路径≤2倍最短路径,保证
O(log n)操作低维护成本:插入/删除最多3次旋转(远少于AVL树)
4. 三树对比总结
| 特性 | B树 | B+树 | 红黑树 |
|---|---|---|---|
| 结构 | 多叉,数据存所有节点 | 多叉,数据仅存叶子 | 二叉,颜色标记平衡 |
| 树高 | 极低(3-4层百万级) | 更低(同数据量更矮) | 较高(约2logN) |
| 磁盘I/O优化 | 优秀 | 最优(索引更紧凑) | 无 |
| 范围查询 | 需中序遍历 | 叶子链表直接遍历 | 需中序遍历 |
| 典型应用 | 文件系统 | MySQL索引 | Java TreeMap |
二、操作复杂度与设计逻辑
1. B/B+树:
减少I/O次数:
节点大小 ≈ 磁盘页(如4KB),单次I/O加载数百键值
二叉查找树需
O(log n)次I/O,B树仅需O(log_m n)(m为分支因子)
插入/删除逻辑:
节点分裂:键值超限 → 中位数提升至父节点,分裂两子节点
节点合并:键值不足 → 向兄弟节点借键或与父节点合并
2. 红黑树:
旋转与变色策略:
插入5种Case:如叔节点红则变色;叔节点黑则旋转(左旋/右旋)
删除7种Case:根据兄弟节点颜色调整(如兄弟红则旋转+变色)
平衡代价:
查询:
O(log n)(常数比AVL大)插入/删除:旋转次数
O(1),优于AVL树的O(log n)
三、应用场景解析
1. B树:文件系统
代表:NTFS、Ext4
原因:
文件块存储分散,B树局部修改特性减少磁盘写入
目录结构需快速定位分散存储的文件块
2. B+树:数据库索引
代表:MySQL InnoDB
原因:
范围查询高效:WHERE id BETWEEN 100 AND 200 → 叶节点链表遍历
聚簇索引优化:叶节点直接存行数据,避免二次查找
3. 红黑树:内存数据结构
代表:Java TreeMap、C++ std::map
原因:
插入/删除频繁(如HashMap冲突链转树)
避免AVL树严格平衡的高维护成本
四、常见问题总结
Q1:数据库为什么用B+树不用红黑树?
A:核心在于磁盘I/O优化和范围查询支持:
I/O次数:红黑树树高约
2logN,百万数据需20次I/O;B+树树高仅3-4层(节点存数百键)。范围查询:B+树叶节点链表直接遍历;红黑树需中序遍历(回溯栈易溢出)。
数据局部性:B+树非叶节点纯索引,单页缓存更多键值,缩小查找范围。
Q2:B树和B+树区别?
A:聚焦数据存储位置与叶子结构:
数据存储:B树所有节点存数据;B+树数据仅存叶子,非叶节点为索引。
叶子链接:B+树叶节点双向链表支持顺序访问;B树叶节点独立。
查询稳定性:B树查询可能在非叶节点结束;B+树必须到叶子(稳定O(log n))。
Q3:红黑树如何保证平衡?
A:通过颜色约束与旋转策略:
黑高平衡:任意路径黑节点数相同,确保最长路径≤2倍最短路径。
旋转Case:插入分5种情况(如叔节点红则变色,黑则旋转);删除分7种(兄弟节点颜色决定操作)。
低开销:插入/删除最多3次旋转(AVL可能需O(log n)次)。
