300.最长递增子序列，674. 最长连续递增序列，

300.最长递增子序列

思路：

1. dp数组定义

这是关键，不清楚dp数组的定义的话，后续无法开展。

dp[i]：表示以nums[i]为结尾的最长子序列长度

2. dp初始化

dp数组长度为nums数组的长度，其中每个元素都初始化为1，因为如果每个元素都取自己的话，那最长子序列长度就是其本身。

3. 递推公式

递推公式也是重点，关键得意识到一个指针解决不了，需要两个指针，一个指针定位当前nums[i]，另一个指针去遍历nums[i]之前的元素，判断之前的最长子序列长度能否容纳下nums[i]。

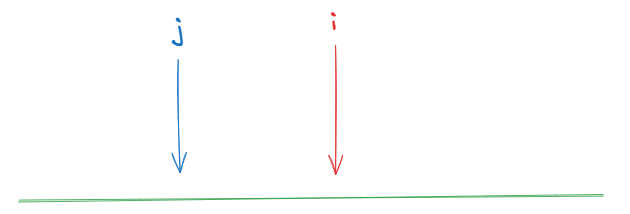
if nums[i] > nums[j]:

        dp[i] = max(dp[j]+1, dp[i]]

dp[i] = dp[j] + 1：表示在dp[j]的最长子序列上，把nums[i]纳入到子序列尾部，可以构成一个更长的子序列长度。

dp[i] = dp[i]：表示dp[i]的最长子序列长度，因为遍历顺序是从左向右的，因此dp[i]在 j 的循环内就被附初始值了，此时就要判断我以哪个 j 位置开始的子序列长度可以使得我第i个位置的子序列长度最长，实际上dp[i] = max(dp[j] + 1, dp[i]), 是判断当前 j 位置纳入 nums[i] 后，和之前其他 j 之前的位置纳入 nums[i] 后的所得到最长子序列。以下这个例子可以观察为什么不是dp[i] = max(dp[j]+1, dp[j] )

nums = [0,1,0,3,2,3]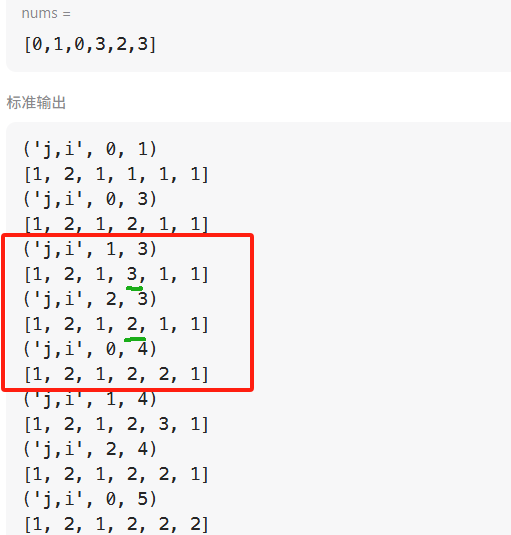

如果是dp[i] = dp[j], 那当前 j 位置的dp数组信息就会把之前的最长子序列长度给覆盖掉了。

4. 遍历顺序

题目是从左往右，因此遍历也是从左往右

5. 打印dp数组

这里也有个坑，因为背包问题和股票问题都是判断最后操作时所能达到的价值，这跟dp数组的定义是紧密相关的。而这道题的dp数组定义是dp[i] = 以nums[i]为结尾的最长子序列长度。但你最长的子序列长度并不一定是以最后一个元素nums[-1]进行结尾的，因此要return的应该是dp数组里的最大值，而不是return dp[-1]。
Code

class Solution(object):def lengthOfLIS(self, nums):""":type nums: List[int]:rtype: int"""# 1. dp数组定义# dp[i]：表示以nums[i]为结尾的最长子序列长度；# 2. 递推公式# if nums[i] > nums[j] then dp[i] = max(dp[j]+1, dp[j]), 对dp数组定义理解不到位# if nums[i] > nums[j] then dp[i] = max(dp[j]+1, dp[i])# 3. 初始化# dp[0:len(nums)] = 1# 4. 遍历顺序# 从左到右# 5. 打印dpdp = [1] * len(nums)for i in range(1, len(nums)):for j in range(i):if nums[i] > nums[j]:dp[i] = max(dp[j]+1, dp[j])print("j,i", j, i)# print(dp)# return dp[-1]    ## 错误输出，对dp数组的定义理解不到位return max(dp[0:len(nums)]) 

674. 最长连续递增序列

思路：

与上道题的操作还是差不多的，关键在于是连续，即dp[j] 纳入nums[i]后构成最长子序列长度后，i和 j 一定是相邻的关系。

Code

class Solution(object):def findLengthOfLCIS(self, nums):""":type nums: List[int]:rtype: int"""# 1. dp数组定义# dp[i]: 以nums[i]结尾的最长子序列长度# 2. 递推公式# if nums[i] > nums[j] and i == j+1 then dp[i] = max(dp[j]+1, dp[i])# 3. 初始化，初始为1# 4. 遍历顺序，从左到右# 5. 打印dp，输出dp数组中的最大值dp = [1] * len(nums)for i in range(len(nums)):for j in range(i):if nums[i] > nums[j] and i == j + 1:dp[i] = max(dp[j]+1, dp[i])return max(dp)

上述代码可以进行优化，因为只需要判断相邻的情况，因此第二个循环很多都是非必要的，这样的话可以缩成一个循环进行操作就行。

Code

class Solution(object):def findLengthOfLCIS(self, nums):""":type nums: List[int]:rtype: int"""# 1. dp数组定义# dp[i]: 以nums[i]结尾的最长子序列长度# 2. 递推公式# if nums[i] > nums[j] and i == j+1 then dp[i] = max(dp[j]+1, dp[i])# 3. 初始化，初始为1# 4. 遍历顺序，从左到右# 5. 打印dp，输出dp数组中的最大值dp = [1] * len(nums)for i in range(1, len(nums)):if nums[i] > nums[i-1]:dp[i] = max(dp[i-1]+1, dp[i])return max(dp)

思路：

关键在于dp数组的定义，要想明白为什么这么定义。

1. dp数组定义

dp[i][j] 表示以nums1[i-1]为结尾的，和以nums2[j-1]为结尾的最长公共子序列。为什么这样表示？这样表示的原因主要是为了避免手动初始化，因为第一行和第一列是无意义的。参考Code1

如果你dp[i][j] 表示以nums1[i]为结尾的，和以nums2[j]为结尾的最长公共子序列，那么初始化就要手动操作。参考Code2

Code1

class Solution(object):def findLength(self, nums1, nums2):""":type nums1: List[int]:type nums2: List[int]:rtype: int"""# 1. dp数组定义# 由于公共子序列顺序的一致的，因此这里的最长子序列是连续的，参考Leetcode 674# dp[i][j]，表示以nums1[i-1]为结尾的，和以nums2[j-1]为结尾的最长公共子序列# 2. 递推公式# if nums1[i-1] == nums2[j-1]: then dp[i][j] = dp[i-1][j-1] + 1# 3. 初始化# 第一行和第一列初始化为0# 4. 遍历顺序# 5. 打印dp数组# 由于最长公共子序列长度并不一定包含最后的nums1[-1]和nums2[-1]，因此需要遍历整个二维数组，得到其中的最大值row = len(nums1) + 1vertical = len(nums2) + 1dp = [ [0] * (vertical) for _ in range(row) ]    ## nums1是行，nums2是列for i in range(1, row):for j in range(1, vertical):if nums1[i-1] == nums2[j-1]:dp[i][j] = dp[i-1][j-1] + 1max_value = -1 for i in range(row):max_value = max(max_value, max(dp[i]))  ## 获得每一行的最大值# print(dp)return max_value

Code2

class Solution(object):def findLength(self, nums1, nums2):""":type nums1: List[int]:type nums2: List[int]:rtype: int"""dp =[[0] * len(nums2) for _ in range(len(nums1))]for i in range(len(nums1)):if nums1[i] == nums2[0]:dp[i][0] = 1for j in range(len(nums2)):if nums2[j] == nums1[0]:dp[0][j] = 1for i in range(1, len(nums1)):for j in range(1, len(nums2)):if nums1[i] == nums2[j]:dp[i][j] = dp[i-1][j-1] + 1max_value = -1 for i in range(len(nums1)):max_value = max(max_value, max(dp[i]))  ## 获得每一行的最大值# print(dp)return max_value