初识opencv04——图像预处理3

初识opencv

初识opencv01——基本api操作
初识opencv02——图像预处理1
初识opencv03——图像预处理2

---

---

一、图像梯度处理

1.1 图像梯度

把图片想象成连续函数，因为边缘部分的像素值是与旁边像素明显有区别的，所以对图片局部求极值，就可以得到整幅图片的边缘信息了。不过图片是二维的离散函数，导数就变成了差分，这个差分就称为图像的梯度。

求图像梯度的本质，就是利用一阶导数（通过有限差分近似）的概念，计算图像这个二维函数在每个像素点上灰度值变化最剧烈的方向和强度。

1.2 边缘提取

对于下图：

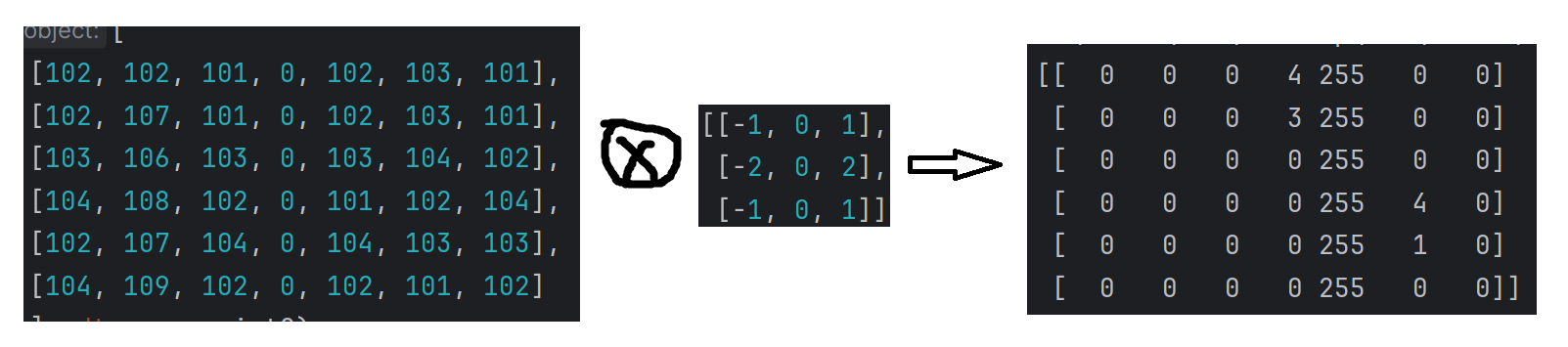
其中，$\left[\begin{array}{ccc}-1& 0& 1\\ -2& 0& 2\\ -1& 0& 1\end{array}\right]$称之为卷积核，该过程即为提取图像的垂直边缘，把该矩阵转置一下，就是提取水平边缘。具体如下：

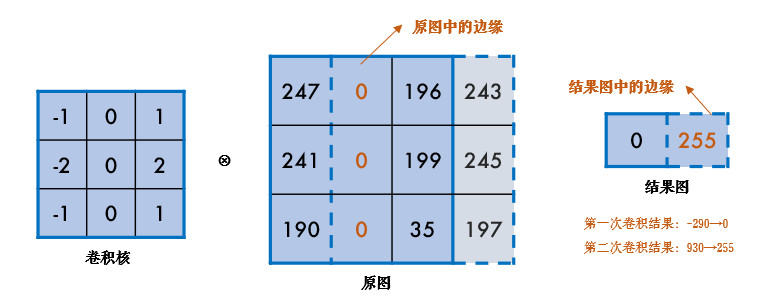
示例代码：

import cv2 as cv
import numpy as npimg=cv.imread('./imageBase/images/shudu.png',cv.IMREAD_GRAYSCALE)
# 定义卷积核-垂直边缘提取
kernel_v=np.array([[-1,0,1],[-2,0,2],[-1,0,1]],dtype=np.float32)
dst=cv.filter2D(img,-1,kernel_v)cv.imshow('img',img)
cv.imshow('dst',dst)
# 水平边缘提取
dst2=cv.filter2D(img,-1,kernel_v.T)
cv.imshow('dst2',dst2)cv.waitKey(0)
cv.destroyAllWindows()

运行结果如下：

原图	垂直边缘提取	水平边缘提取

其中用到的api有：

• cv2.filter2D(src, ddepth, kernel)
  ilter2D函数是用于对图像进行二维卷积（滤波）操作。它允许自定义卷积核（kernel）来实现各种图像处理效果，如平滑、锐化、边缘检测等

其参数分别为：

• src: 输入图像，一般为numpy数组。
• ddepth: 输出图像的深度，可以是负值（表示与原图相同）、正值或其他特定值（常用-1 表示输出与输入具有相同的深度）。
• kernel: 卷积核，一个二维数组（通常为奇数大小的方形矩阵），用于计算每个像素周围邻域的加权和。

1.3 sobel算子

上面的两个卷积核都叫做Sobel算子，只是方向不同，垂直方向上计算所得值叫垂直梯度$G_x=k_1\times src$，水平方向上计算所得值叫水平梯度$G_y=k_2\times src$，故总梯度为$G=\sqrt{G{x}^2+G{y}^2}$。

import cv2 as cv
import numpy as npimg=cv.imread('./imageBase/images/shudu.png',cv.IMREAD_GRAYSCALE)
sobel_x=cv.Sobel(img,-1,1,0,ksize=3)
sobel_y=cv.Sobel(img,-1,0,1,ksize=3)
cv.imshow('img',img)
cv.imshow('sobel_x',sobel_x)
cv.imshow('sobel_y',sobel_y)
cv.waitKey(0)
cv.destroyAllWindows()

运行结果如下：

其中用到的api有：

• sobel_image = cv2.Sobel(src, ddepth, dx, dy, ksize)
  各个参数含义如下：

src：这是输入图像，通常应该是一个灰度图像（单通道图像），因为 Sobel 算子是基于像素亮度梯度计算的。在彩色图像的情况下，通常需要先将其转换为灰度图像。
ddepth：这个参数代表输出图像的深度，即输出图像的数据类型。在 OpenCV 中，-1 表示输出图像的深度与输入图像相同。
dx,dy：当组合为dx=1,dy=0时求x方向的一阶导数，在这里，设置为1意味着我们想要计算图像在水平方向（x轴）的梯度。当组合为 dx=0,dy=1时求y方向的一阶导数（如果同时为1，通常得不到想要的结果,想两个方向都处理的比较好 学习使用后面的算子）
ksize：Sobel算子的大小，一般为奇数，默认为3。

1.4 laplacian算子

在图像中我们也可通过二阶导来计算梯度，即图像间像素值差分间的差分。故我们可以使用Laplacian 算子来测量的是图像灰度的二阶导数，即灰度变化的变化率。

示例代码如下：

import cv2 as cv
import numpy as npimg=cv.imread('./imageBase/images/shudu.png',cv.IMREAD_GRAYSCALE)
laplacian=cv.Laplacian(img,-1,ksize=3)
cv.imshow('img',img)
cv.imshow('laplacian',laplacian)
cv.waitKey(0)
cv.destroyAllWindows()

运行结果如下：

其中用到的api有：

• cv2.Laplacian(src, ddepth)
  其参数含义为：

src：这是输入图像
ddepth：这个参数代表输出图像的深度，即输出图像的数据类型。在 OpenCV 中，-1 表示输出图像的深度与输入图像相同。

laplacian算子卷积核的简单推导

一维的一阶和二阶差分公式分别为：
$$\frac{\partial f}{\partial x}=f(x+1)-f(x)$$
$$\frac{{\partial }^{2}f}{\partial x^2}=f(x+1)+f(x-1)-2f(x)$$

其中$f(x+1)+f(x-1)-2f(x)$实际上是差分$f(x+1)-f(x)$与差分$f(x)-f(x-1)$的差分。

提取前面的系数，那么一维的Laplacian滤波核是（之所以是一维，是因为只有一个自变量x，系数仍然是二阶导的，分别对应于x-1，x，x+1）：
$$k=[1-21]$$
而对于二维函数f(x,y)，两个方向的二阶差分分别是：
$$\frac{{\partial }^{2}f}{\partial x^2}=f(x+1,y)+f(x-1,y)-2f(x,y)$$
$$\frac{{\partial }^{2}f}{\partial y^2}=f(x,y+1)+f(x,y-1)-2f(x,y)$$
若要通过二阶导求梯度则有
$$dst=\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}$$
合在一起就是：
$$V^{2}f(x,y)=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)$$
同样提取前面的系数，那么二维的Laplacian滤波核就是：
$$k=\left[\begin{array}{ccc}0& 1& 0\\ 1& -4& 1\\ 0& 1& 0\end{array}\right]$$
这就是Laplacian算子的图像卷积模板，有些资料中在此基础上考虑斜对角情况，将卷积核拓展为：
$$k=\left[\begin{array}{ccc}1& 1& 1\\ 1& -8& 1\\ 1& 1& 1\end{array}\right]$$
其中需要注意的是，若要推导出这个结果，对角线的权重应当近似得看作与垂直或水平方向一样。

1.5 补充

• Prewitt算子，只利用邻域间的原始差值来检测边缘：
  $$k=\left[\begin{array}{rrr}-1& 0& 1\\ -1& 0& 1\\ -1& 0& 1\end{array}\right]$$
• Scharr算子，sobel算子改进型
  $$k=\left[\begin{array}{rrr}-3& 0& 3\\ -10& 0& 10\\ -3& 0& 3\end{array}\right]$$

二、图像边缘处理

图像边缘处理不是一个算子，是完整的一整套方案，这里以canny图像边缘检测算法过程为例。

由于边缘检测本身属于锐化操作，对噪点比较敏感，所以需要进行平滑处理。故在canny算法中一般需要先用高斯滤波进行处理，这里不再赘述具体细节。

2.1 计算图像梯度及其方向

这里使用了sobel算子来计算图像的梯度值，其中：
$$sobel(水平方向)=\left[\begin{array}{ccc}-1& 0& 1\\ -2& 0& 2\\ -1& 0& 1\end{array}\right]$$
$$sobel(垂直方向)=\left[\begin{array}{ccc}-1& -2& -1\\ 0& 0& 0\\ 1& 2& 1\end{array}\right]$$
然后梯度可由此计算得出：$G=\sqrt{G_x{}^2+G_y{}^2}$

但在OpenCV中，默认使用G=|G_{x}+G_{y}|来计算梯度值

同时，我们也可通过$\theta =\arctan (\frac{G_{\mathrm{y}}}{G_x})$求得一个角度值，来表示当前边缘的梯度的方向。

并且如果梯度方向不是0°、45°、90°、135°这种特定角度，那么就要用到插值算法来计算当前像素点在其方向上进行插值的结果了，然后进行比较并判断是否保留该像素点。

不过为了便于计算，我们一般将将边缘方向分为四个方向：水平方向、垂直方向、45°方向、135°方向，即：

• 当$\theta$值为-22.5°~22.5°，或-157.5°~157.5°，则认为边缘为水平边缘；
• 当法线方向为22.5°~67.5°，或-112.5°~-157.5°，则认为边缘为45°边缘；
• 当法线方向为67.5°~112.5°，或-67.5°~-112.5°，则认为边缘为垂直边缘；
• 当法线方向为112.5°~157.5°，或-22.5°~-67.5°，则认为边缘为135°边缘；

2.2 非极大值抑制

由于图片进行过高斯滤波，可能会导致原本清晰的边缘变得模糊，即得到的边缘像素点非常多。这里我们就需要进行非极大值抑制，来去除伪边缘使边缘尽可能细一点。

在该步骤中，我们需要检查每个像素点的梯度方向上的相邻像素，并保留梯度值最大的像素，将其他像素抑制为零。

假设当前像素点为（x，y），其梯度方向是0°，梯度值为G（x，y），那么我们就需要比较G（x，y）与两个相邻像素的梯度值：G（x-1，y）和G（x+1，y）。如果G（x，y）是三个值里面最大的，就保留该像素值，否则将其抑制为零。

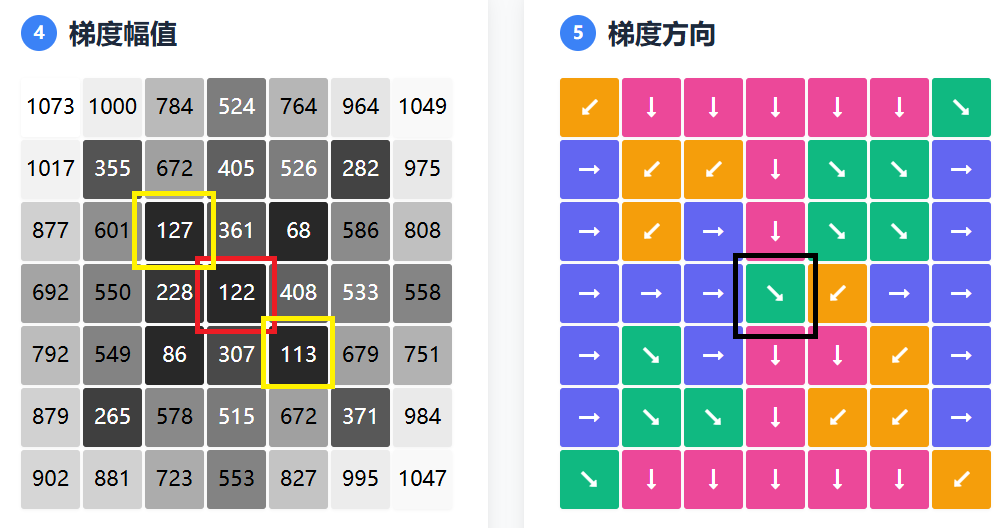
以上图为例，图像正中红框处的像素的梯度值为122，其梯度方向为135°边缘。故需要将其与图中黄框的像素对比，其梯度值不为最大，将其将其抑制为零。对其余所有像素重复以上操作，结果如下：

2.3 api和使用

以下为示例代码：

# 读图
import cv2 as cv
import numpy as npimg=cv.imread('./imageBase/images/shudu.png',cv.IMREAD_GRAYSCALE)
cv.imshow('img',img)# 二值化
ret,img=cv.threshold(img,0,255,cv.THRESH_BINARY+cv.THRESH_OTSU)# 使用canny边缘处理
canny=cv.Canny(img,100,200)
cv.imshow('canny',canny)# 显示效果
cv.waitKey(0)
cv.destroyAllWindows()

运行结果：

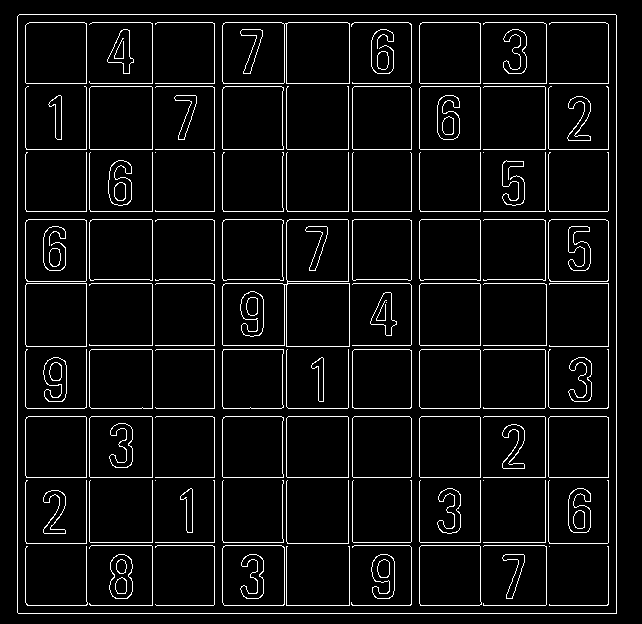
其中用到的api有：

• edges = cv2.Canny(image, threshold1, threshold2)
  即使读到的是彩色图也可以进行处理。

• image：输入的灰度/二值化图像数据。
• threshold1：低阈值，用于决定可能的边缘点。
• threshold2：高阈值，用于决定强边缘点。

三、绘制图像轮廓

3.1 什么是轮廓

轮廓是一系列相连的点组成的曲线，代表了物体的基本外形。轮廓不等于边缘，相对于边缘，轮廓是连续的，边缘不一定连续，如下图所示。轮廓是一个闭合的、封闭的形状。

• 轮廓的作用：
  • 形状分析
  • 目标识别
  • 图像分割

3.2 寻找轮廓

在OpenCV中，使用cv2.findContours()来进行寻找轮廓，其原理这里不做介绍，具体的实现原理可参考：OpenCV轮廓提取算法详解findContours()

其函数原型为
contours,hierarchy = cv2.findContours(image，mode，method)

• 返回值：contours为[ 轮廓点坐标 ] ，hierarchy为 [ 层级关系 ]。
• contours：表示获取到的轮廓点的列表。检测到有多少个轮廓，该列表就有多少子列表，每一个子列表都代表了一个轮廓中所有点的坐标。
• hierarchy：表示轮廓之间的关系。对于第i条轮廓，$hierarchy[i][0]$, $hierarchy[i][1]$ , $hierarchy[i][2]$ ,$
  hierarchy[i][3]$分别表示其后一条轮廓、前一条轮廓、（同层次的第一个）子轮廓、父轮廓的索引（如果没有相应的轮廓，则对应位置为-1）。该参数的使用情况会比较少。
• image：表示输入的二值化图像。
• mode：表示轮廓的检索模式。
• method：轮廓的表示方法。

其中：

1. mode参数
   轮廓查找方式，返回不同的层级关系，共有四个选项分别为：RETR_LIST，RETR_EXTERNAL，RETR_CCOMP，RETR_TREE。

   1. RETR_EXTERNAL
      表示只查找最外层的轮廓。并且在hierarchy里的轮廓关系中，每一个轮廓只有前一条轮廓与后一条轮廓的索引，而没有父轮廓与子轮廓的索引。

   2. RETR_LIST
      表示列出所有的轮廓。并且在hierarchy里的轮廓关系中，每一个轮廓只有前一条轮廓与后一条轮廓的索引，而没有父轮廓与子轮廓的索引。

   3. RETR_CCOMP
      表示列出所有的轮廓。并且在hierarchy里的轮廓关系中，轮廓会按照成对的方式显示。在 RETR_CCOMP 模式下，轮廓被分为两个层级：

      • 层级 0：所有外部轮廓（最外层的边界）。
      • 层级 1：所有内部轮廓（孔洞或嵌套的区域）。

   4. RETR_TREE
      表示列出所有的轮廓。并且在hierarchy里的轮廓关系中，轮廓会按照树的方式显示，其中最外层的轮廓作为树根，其子轮廓是一个个的树枝。

• method参数
  轮廓存储方法，或轮廓近似方法。决定如何简化轮廓点的数量。就是找到轮廓后怎么去存储这些点。有三个选项：CHAIN_APPROX_NONE、CHAIN_APPROX_SIMPLE、CHAIN_APPROX_TC89_L1。
  • CHAIN_APPROX_NONE表示将所有的轮廓点都进行存储
  • CHAIN_APPROX_SIMPLE表示只存储有用的点，比如直线只存储起点和终点，四边形只存储四个顶点，默认使用这个方法；

对于mode和method这两个参数来说，一般使用RETR_EXTERNAL和CHAIN_APPROX_SIMPLE这两个选项。

3.3 绘制轮廓

轮廓找出来后，其实返回的是一个轮廓点坐标的列表，因此我们需要根据这些坐标将轮廓画出来，因此就用到了绘制轮廓的方法。

以下为示例代码：

# 读图
import cv2 as cv
import numpy as npimg=cv.imread('./imageBase/images/num.png')
# 灰度化
gray=cv.cvtColor(img,cv.COLOR_BGR2GRAY)
# 二值化
ret,thresh=cv.threshold(gray,0,255,cv.THRESH_BINARY_INV+cv.THRESH_OTSU)
cv.imshow('thresh',thresh)
# 寻找轮廓
contours,hierarchy=cv.findContours(thresh,cv.RETR_TREE,cv.CHAIN_APPROX_SIMPLE)
print(len(contours),hierarchy)# 绘制轮廓
cv.drawContours(img,contours,-1,(0,255,0),3)
cv.imshow('img',img)cv.waitKey(0)
cv.destroyAllWindows()

运行结果为：


其中用到的api有：

• cv2.drawContours(image, contours, contourIdx, color, thickness)
  其各个参数含义如下：

• image：原始图像，一般为单通道或三通道的 numpy 数组。
• contours：包含多个轮廓的列表，每个轮廓本身也是一个由点坐标构成的二维数组（numpy数组）。
• contourIdx：要绘制的轮廓索引。如果设为 -1，则会绘制所有轮廓。根据索引找到轮廓点绘制出来。默认是-1。
• color：绘制轮廓的颜色，可以是 BGR 值或者是灰度值（对于灰度图像）。
• thickness：轮廓线的宽度，如果是正数，则画实线；如果是负数，则填充轮廓内的区域。

四、凸包特征检测

通俗的讲，凸包其实就是将一张图片中物体的最外层的点连接起来构成的凸多边形，它能包含物体中所有的内容。对于一个点集来说，如果该点集存在凸包，那么这个点集里面的所有点要么在凸包上，要么在凸包内。

凸包检测常用在物体识别、手势识别、边界检测等领域。

• 穷举法
• QuickHull法

由于穷举法本身效率较低，并不常用，这里仅作了解。

• 将集中的点进行两两配对，并进行连线，对于每条直线，检查其余所有的点是否处于该直线的同一侧，如果是，那么说明构成该直线的两个点就是凸包点，其余的线依次进行计算，从而获取所有的凸包点。

4.1 QuickHull法

其基本流程为：

• 将所有点放在二维坐标系中，找到横坐标最小和最大的两个点$P_1$和$P_2$并连线。此时整个点集被分为两部分，直线上为上包，直线下为下包。
• 以上包为例，找到上包中的点距离该直线最远的点$P_3$,连线并寻找直线$P1P3$左侧的点和$P2P3$右侧的点，然后重复本步骤，直到找不到为止。对下包也是这样操作。

以以下点集为例：

点集

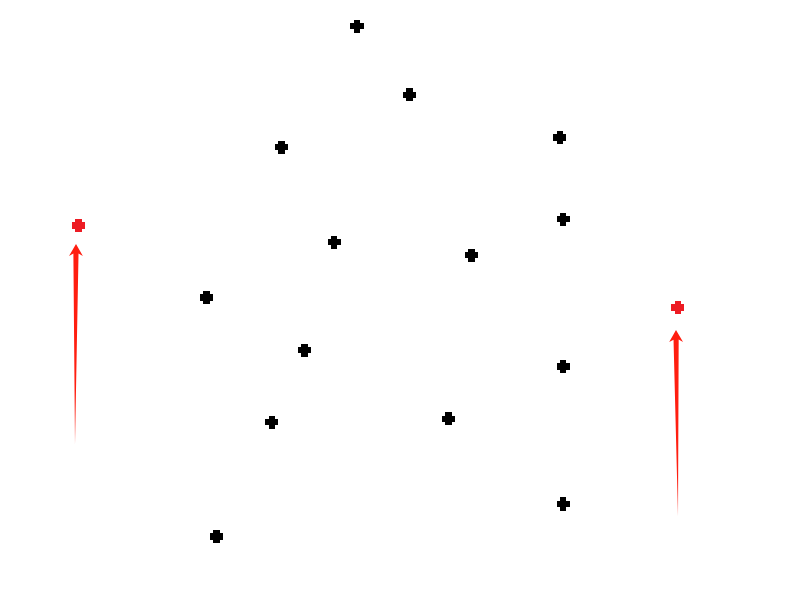
寻找处于最左边和最右边的点

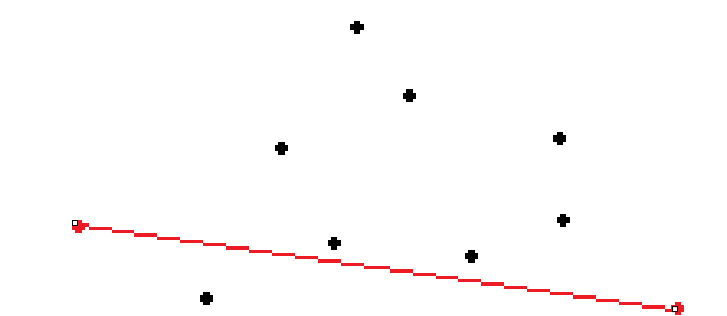
将这两个点连接，并将点集分为上半区和下半区

这里先以上半区为例：

找到上面这些点离直线最远的点，将其与左右两点连起来

重复以上步骤，直到无法在多边形外找到点为止。最终结果如下：

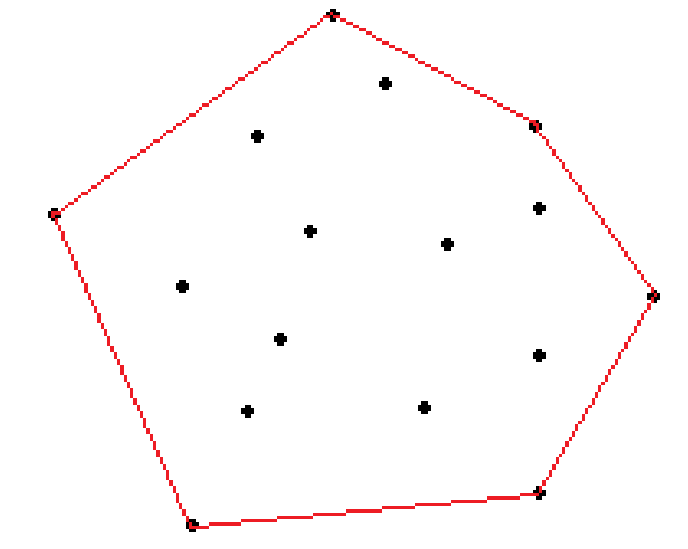
4.2 获取凸包点与绘制凸包

以下为示例代码：

import cv2 as cv
import numpy as np# 读图
img=cv.imread('./imageBase/images/tu.png')
# 灰度化
gray=cv.cvtColor(img,cv.COLOR_BGR2GRAY)
# 二值化
ret,thresh=cv.threshold(gray,0,255,cv.THRESH_BINARY+cv.THRESH_OTSU)
# 寻找轮廓
contours,hierarchy=cv.findContours(thresh,cv.RETR_EXTERNAL,cv.CHAIN_APPROX_SIMPLE)
# 获取凸包点
hull=cv.convexHull(contours[0])
cv.polylines(img,[hull],True,(0,255,0),3)
cv.imshow('img',img)cv.waitKey(0)
cv.destroyAllWindows()

原图	其凸包
其中用到的api有：

• cv2.convexHull(points)
  points：输入参数，图像的轮廓
• cv2.polylines(image, pts, isClosed, color, thickness=1)

• image：要绘制线条的目标图像，它应该是一个OpenCV格式的二维图像数组（如numpy数组）。
• pts：一个二维 numpy 数组，每个元素是一维数组，代表一个多边形的一系列顶点坐标。
• isClosed：布尔值,表示是否闭合多边形,如果为 True，会在最后一个顶点和第一个顶点间自动添加一条线段，形成封闭的多边形。
• color：线条颜色，可以是一个三元组或四元组，分别对应BGR或BGRA通道的颜色值，或者是灰度图像的一个整数值。
• thickness（可选）：线条宽度，默认值为1。

五、图像轮廓特征查找

图像轮廓特征查找其实就是他的外接轮廓。常用外接轮廓有外接矩形、最小外接矩形、最小外接圆

应用：

• 图像分割
• 形状分析
• 物体检测与识别

以下为示例代码：

# 读图
img=cv.imread('./imageBase/images/num.png')
# 灰度化
gray=cv.cvtColor(img,cv.COLOR_BGR2GRAY)
# 二值化
ret,thresh=cv.threshold(gray,0,255,cv.THRESH_BINARY_INV+cv.THRESH_OTSU)
# 寻找轮廓
contours,hierarchy=cv.findContours(thresh,cv.RETR_TREE,cv.CHAIN_APPROX_SIMPLE)for cnt in contours:# 获取外接矩形x,y,w,h=cv.boundingRect(cnt)# 绘制外接矩形-绿色形框cv.rectangle(img,(x,y),(x+w,y+h),(0,255,0),2,cv.LINE_AA)# 获取最小外接矩形rect=cv.minAreaRect(cnt)box=cv.boxPoints(rect).astype('int')# 绘制最小外接矩形-蓝色形框cv.drawContours(img,[box],0,(255,0,0),2)# 获取最小外接圆(x,y),radius=cv.minEnclosingCircle(cnt)# 绘制最小外接圆-红色圆框center=(int(x),int(y))radius=int(radius)cv.circle(img,center,radius,(0,0,255),2)cv.imshow('img',img)cv.waitKey(0)
cv.destroyAllWindows()

运行结果为：

其中用到的api有：

• boundingRect(轮廓点)
• rect = cv2.minAreaRect(cnt)
  传入的cnt参数为contours中的轮廓,可以遍历contours中的所有轮廓,然后计算出每个轮廓的小面积外接矩形
  • rect 是计算轮廓最小面积外接矩形:rect 结构通常包含中心点坐标 (x, y)、宽度 width、高度 height 和旋转角度 angle
• cv2.boxPoints(rect).astype(int)
  cv2.boxPoints(rect)返回 是一个形状为 4行2列的数组，每一行代表一个点的坐标（x, y），顺序按照逆时针或顺时针方向排列。将最小外接矩形转换为边界框的四个角点，并转换为整数坐标
• (x,y),radius=cv.minEnclosingCircle(cnt)
  • 输入：一个轮廓点集 cnt（由 cv.findContours() 检测得到）
  • 输出：(x, y)：最小外接圆的圆心坐标（浮点数）；radius：最小外接圆的半径（浮点数）

---

总结

本文章简要介绍了OpenCV图像预处理中的图像梯度处理、图像边缘处理、绘制图像轮廓、凸包特征检测、图像轮廓特征查找。