弹性网：基于神经网络的多组分磁共振弹性成像波反演与不确定性量化|文献速递-医学影像算法文献分享

Title

题目

ElastoNet: Neural network-based multicomponent MR elastography waveinversion with uncertainty quantification

弹性网：基于神经网络的多组分磁共振弹性成像波反演与不确定性量化

01

文献速递介绍

磁共振弹性成像（MRE）是一种成熟的非侵入性成像技术，用于量化软组织的力学特性（Muthupillai 等人，1995；Sack，2022）。准确表征组织刚度对于诊断和监测多种疾病（如肝纤维化）至关重要（Morisaka 等人，2017）。 在 MRE 中，机械振动会产生声波，这些声波可探测软组织的力学特性。由此产生的组织位移通过双极运动编码梯度（MEGs）被编码到复杂 MRI 信号的相位中。所获得的波图像反映了沿 MEG 方向的波场分量，通过反演算法可将其转换为刚度图。由于未知的边界条件、噪声和压缩波的存在，MRE 中的逆问题求解具有不适定性（Sack，2022）。因此，MRE 反演方法通常需要针对特定的实验设置进行调整，这些设置涉及图像分辨率、信噪比（SNR）、波长和振动频率等（Hirsch 等人，2017）。例如，有限差分算子与分辨率不匹配时，在低波数范围内通常会导致刚度值被低估，而当高波数以低空间支持度离散化时，则会出现高估情况（Mura 等人，2020）。 多年来，人们开发并优化了多种 MRE 反演方法。读者可参考该领域众多优秀的综述文章（Doyley，2012；Fovargue 等人，2018）。临床 MRE 研究中使用的主要反演方法基于用于局部频率估计的对数正态滤波器组（LFE）（Knutsson 等人，1994）、多频双弹粘弹性反演（MDEV）（Papazoglou 等人，2012；Hirsch 等人，2013）及其向相位梯度反演方法的扩展，即 k-MDEV（Tzschätzsch 等人，2016）。这些方法均可在 https://bioqic-apps.charite.de 上公开获取，用于基于服务器的 MRE 数据处理和直接对比（Meyer 等人，2022）。 近年来，神经网络在解决 MRE 逆问题方面展现出良好前景（Murphy 等人，2017；Scott 等人，2020，2022；Ma 等人，2023；Ragoza 和 Batmanghelich，2023）。在 Ragoza 和 Batmanghelich（2023）的研究中，利用具有可用真实值的数据集训练了一个物理信息神经网络。然而，与其他计算机视觉任务不同，目前不存在带有经过验证的真实标签的大型实验性 MRE 数据库。这种标记数据的缺乏可通过利用波传播物理原理来合成生成不同波长和方向的小波图像块，以训练神经网络来解决。Murphy 等人（2017）最初提出了这种方法，假设材料为均匀弹性体，并生成 5×5 至 11×11 像素的小波块。Scott 等人（2020）在此基础上进行了扩展，使用耦合谐振子模拟（Braun 等人，2001）并在波块中引入了不均匀性。在后续研究中，他们使用波动方程的有限差分模型并将其应用于脑部 MRE（Scott 等人，2022）。最近，有人提出了一种具有 3×3 像素标准化块大小的均匀粘弹性材料模型，用于基于行波扩展的神经网络（TWENN）（Ma 等人，2023）。 当前基于神经网络的 MRE 反演实现存在明显局限性。多种因素会影响这些方法的性能，从训练协议的选择、神经网络架构到推理过程中的预处理和后处理流程。例如，合成生成的训练波场中不包含压缩波，这就将抑制压缩波的负担转移到了预处理阶段。此外，多组分同步反演能力有限或难以实现，需要单独反演后再进行后验平均。另一个缺点是，与传统方法相比，基于神经网络的反演方法通用性有限，因为到目前为止，神经网络模型必须针对每个特定应用进行训练，并采用固定的 MRE 参数设置（如图像分辨率和激发频率）。 最后，确保预测的可信度对于机器学习在医学成像中的应用至关重要（Gawlikowski 等人，2023）。已有多种方法被提出用于神经网络中的不确定性量化，包括深度证据学习（Soy 等人，2018；Amini 等人，2020）、蒙特卡洛 dropout（Gal 和 Ghahramani，2016）或集成方法（Lakshminarayanan 等人，2017）。将此类方法融入基于神经网络的 MRE 反演中，可能有助于识别对刚度值信心较低的区域。 为克服这些局限性，我们以 TWENN（Ma 等人，2023）开创的方法为基础，提出了 ElastoNet——一种多用途的基于神经网络的 MRE 反演方法，用于重建剪切波速（SWS）以作为刚度的替代指标。ElastoNet 的设计具有以下特点： - 具有普遍适用性，不受激发频率或图像分辨率的限制。 - 无需分离纵波和横波分量，因为在训练数据模型中纳入了压缩波。 - 能够进行多组分波场的同步反演。 - 以可忽略的额外计算成本实现不确定性量化。 在本研究中，我们在合成生成的平面波、有限元模型（FEM）、体模数据以及健康志愿者的腹部在体 MRE 数据上测试了 ElastoNet 的性能，并与两种成熟的反演方法（LFE 和 k-MDEV）以及最近提出的基于神经网络的反演方法 TWENN 进行了对比。为评估 ElastoNet 的通用性，我们分析了宽频带多频率 MRE 数据，频率范围涵盖前所未有的 20 至 80 Hz。

Abatract

摘要

Magnetic Resonance Elastography (MRE) quantifies soft tissue stiffness by measuring induced shear waves.MRE inversion techniques for parameter reconstruction are often affected by noise and compression waves.Neural network-based inversions have emerged as a possible solution to address these challenges. However,current approaches lack generalizability and do not provide uncertainty estimates. Therefore, we proposeElastoNet, a novel neural network-based approach for MRE wave inversion that analyzes multiple wavecomponents independently of resolution and vibration frequency and provides uncertainty quantification maps.ElastoNet was trained on synthetically generated wave patches of 5 × 5 pixels. Uncertainty quantification wasimplemented using evidential deep learning. ElastoNet was evaluated on synthetically generated plane waves,finite element simulations of abdominal MRE, phantom MRE data, and a prospective wideband multifrequencyabdominal MRE study (excitation frequencies of 20 to 80 Hz) in 14 healthy volunteers. ElastoNet was comparedwith established inversion methods LFE and k-MDEV, as well as neural network-based TWENN. ElastoNetgenerated shear wave speed maps as a proxy of stiffness with comparable or better accuracy than establishedmethods and did not require retraining for different resolutions and vibration frequencies. ElastoNet achieveda lower root mean square error relative to ground truth values in finite element simulations and phantom datathan other inversion methods and provided uncertainty maps. ElastoNet is a promising method for universalneural network-based inversion in MRE, effectively overcoming current challenges and expanding the potentialuse of neural networks in diagnostic MRE applications.

磁共振弹性成像（MRE）通过测量诱导剪切波来量化软组织的刚度。用于参数重建的MRE反演技术常受噪声和压缩波的影响。基于神经网络的反演方法已成为应对这些挑战的一种潜在解决方案。然而，现有方法缺乏通用性，且无法提供不确定性估计。因此，我们提出了ElastoNet——一种新型的基于神经网络的MRE波反演方法，它能独立于分辨率和振动频率分析多个波组分，并提供不确定性量化图。 ElastoNet在5×5像素的合成生成波片上进行训练，通过证据深度学习实现不确定性量化。我们在合成生成的平面波、腹部MRE的有限元模拟、体模MRE数据以及一项针对14名健康志愿者的前瞻性宽带多频率腹部MRE研究（激发频率为20至80Hz）中对ElastoNet进行了评估。 将ElastoNet与已有的反演方法LFE、k-MDEV以及基于神经网络的TWENN进行了对比。结果显示，ElastoNet生成的剪切波速度图（作为刚度的替代指标）与现有方法相比，准确率相当或更优，且无需针对不同分辨率和振动频率重新训练。在有限元模拟和体模数据中，与其他反演方法相比，ElastoNet相对于真实值的均方根误差更低，并能提供不确定性图。 ElastoNet是一种很有前景的MRE通用神经网络反演方法，它有效克服了当前存在的挑战，拓展了神经网络在诊断性MRE应用中的潜在用途。

Method

方法

This section describes the development of ElastoNet and the approach we used for evaluation.

2.1. ElastoNet

2.1.1. Synthetically generated training dataset*We trained a neural network on synthetically generated wavepatches of 5 × 5 pixels. Assuming a locally homogeneous, isotropic,and viscoelastic material, we expanded on previous data generationschemes (Baghani et al., 2011; Murphy et al., 2017; Ma et al., 2023)by integrating compression waves into the model. For each componentof the displacement field, the complex wave displacement 𝑢 at a givenlocation 𝒓was expressed as a superposition of multiple shear waves,compression waves, and noise:𝑢 (𝒓) =𝑁s ∑𝑗=1𝑎s𝑗 𝑒−i (( 𝜆 2 s 𝜋 𝑗 −i 𝛿1 s𝑗) 𝒏(𝑑, 𝜃, 𝜑) ⋅ 𝒓𝑗+𝜙s𝑗)+𝑁c ∑𝑗=1𝑎c𝑗 𝑒−i (( 𝜆 2 c 𝜋 𝑗 −i 𝛿c 1 𝑗 ) 𝒏(𝑑, 𝜃, 𝜑) ⋅ 𝒓𝑗 +𝜙c𝑗 )𝜂* (𝒓)(1)where 𝑎s and 𝑎c are the amplitudes of the shear and compression waves,𝜙*s and *𝜙*c are the phases of the shear and compression waves, and 𝑁*sand *𝑁*c are the numbers of superimposed shear and compression wavesources in 3D space. For each wave, the point source is located at adistance *𝑑* from the center pixel of the patch, with the generated wavepropagating in the direction of the normal vector 𝒏 at an in-plane angle𝜃*, and at an out-of-plane angle 𝜑. *𝜆s and 𝜆c are the wavelengths of theshear and compression waves, and 𝛿s and 𝛿c are the penetration lengthsof the shear and compression waves. The noise term 𝜂(𝒓) was chosenas zero-mean Gaussian noise applied to the real and imaginary partsof the wavefield. The data generation process is shown in Fig. 1. Thewavelengths were defined in pixel numbers, ensuring that the data isindependent of the image resolution and excitation frequency. In thegenerated data, the amplitudes, phases, numbers of sources, distancesto the sources, angles of the sources, wavelengths, penetration lengths,and SNR were all drawn randomly from the uniform distribution withinthe ranges defined in Table 1 and cover the realistic ranges for healthyand diseased human tissue.

本节介绍了ElastoNet的开发过程以及我们用于评估的方法。  2.1 ElastoNet 2.1.1 合成生成的训练数据集 我们在5×5像素的合成生成波片上训练神经网络。假设材料是局部均匀、各向同性且粘弹性的，我们在以往数据生成方案（Baghani等人，2011；Murphy等人，2017；Ma等人，2023）的基础上进行了扩展，将压缩波整合到模型中。对于位移场的每个分量，给定位置𝒓处的复波位移\(u\)表示为多个剪切波、压缩波和噪声的叠加： \[ u(\boldsymbol{r}) = \sum_{j=1}^{N_s} a_{s_j} e^{-i\left( \left( \frac{2\pi}{\lambda_s} - i\delta_{s_j} \right) \boldsymbol{n}(d, \theta, \varphi) \cdot \boldsymbol{r}_j + \phi_{s_j} \right)} + \sum_{j=1}^{N_c} a_{c_j} e^{-i\left( \left( \frac{2\pi}{\lambda_c} - i\delta_{c_j} \right) \boldsymbol{n}(d, \theta, \varphi) \cdot \boldsymbol{r}_j + \phi_{c_j} \right)} + \eta(\boldsymbol{r}) \quad (1) \] 其中，\(a_s\)和\(a_c\)分别是剪切波和压缩波的振幅，\(\phi_s\)和\(\phi_c\)分别是剪切波和压缩波的相位，\(N_s\)和\(N_c\)分别是3D空间中叠加的剪切波源和压缩波源的数量。对于每个波，点源位于距波片中心像素距离\(d\)处，生成的波沿法向量𝒏的方向传播，其面内角度为\(\theta\)，面外角度为\(\varphi\)。\(\lambda_s\)和\(\lambda_c\)分别是剪切波和压缩波的波长，\(\delta_s\)和\(\delta_c\)分别是剪切波和压缩波的穿透长度。噪声项\(\eta(\boldsymbol{r})\)选择为施加于波场实部和虚部的零均值高斯噪声。数据生成过程如图1所示。波长以像素数定义，确保数据独立于图像分辨率和激发频率。在生成的数据中，振幅、相位、源数量、到源的距离、源角度、波长、穿透长度和信噪比均从表1定义范围内的均匀分布中随机抽取，且涵盖健康和患病人体组织的实际范围。

Conclusion

结论

In summary, we presented ElastoNet, a universally applicable neuralnetwork-based inversion method. Through resolution and frequencyindependence as well as training on a wide range of syntheticallygenerated mechanical properties, ElastoNet requires no retraining fordifferent use cases or tuning of pre- or post-processing steps to differentMRE datasets. Moreover, the method provides a direct quantification ofthe uncertainty of its predictions for improved reliability of local SWSvalues. ElastoNet contributes to the further development of reliableneural network-based MRE inversions by addressing current limitationsof state-of-the-art inversion methods, in particular, for the analysis ofwideband multifrequency MRE data acquired in abdominal organs.

总之，我们提出了ElastoNet——一种具有普遍适用性的基于神经网络的反演方法。凭借分辨率与频率无关的特性，以及在多种合成生成的力学特性数据上进行的训练，ElastoNet无需针对不同使用场景重新训练，也无需根据不同MRE数据集调整预处理或后处理步骤。此外，该方法能够直接量化预测结果的不确定性，从而提高局部剪切波速（SWS）值的可靠性。   ElastoNet通过解决现有主流反演方法的局限性（尤其是在分析腹部器官宽频带多频率MRE数据方面），为基于神经网络的可靠MRE反演方法的进一步发展做出了贡献。

Results

结果

3.1. Synthetically generated plane wave dataset

Using the synthetically generated plane wave model described inSection 2.2.1, we analyzed the performance of ElastoNet on thesedata. Fig. 3a shows examples of wave images obtained at differentnumbers of wavelengths per window. Fig. 3b displays the predictedSWS normalized for a given SWS of 1 m/s at different numbers ofwavelengths per window for LFE, k-MDEV, TWENN, and ElastoNet, aswell as the ground truth.For a number of wavelengths per window <1, the root mean squareerror (RMSE) was 0.22, 0.25, 0.55, and 0.31 m/s for k-MDEV, LFE,TWENN, and ElastoNet, respectively. For a number of wavelengths perwindow ≥1, the RMSE was 0.01, 0.02, 0.08, and 0.01 m/s for k-MDEV,LFE, TWENN, and ElastoNet. While for a number of wavelengths perwindow <1, the predicted values were consistently underestimatedby all methods, ElastoNet outperformed TWENN in this domain witha lower RMSE. ElastoNet showed the lowest RMSE for a number ofwavelengths per window ≥1, along with k-MDEV.Fig. 3b also displays the results of the ablation study performed onElastoNet. It yielded that when single MEG components were providedas input to the model with posterior averaging instead of all threeMEG components directly, for a number of wavelengths per window<*1, the RMSE was 0.36 m/s rather than 0.22 m/s and for a numberof wavelengths per window ≥1, the RMSE was 0.04 m/s rather than0.01 m/s.Fig. 3c shows the effects on the predicted SWS, reconstruction error,and uncertainty of the different signal amplitudes and noise levels fora wave image with 2.5 wavelengths per window. The results for waveimages with 0.5 to 5 wavelengths per window in increments of 0.5 areprovided as supplementary materials

利用2.2.1节所述的合成生成平面波模型，我们对ElastoNet在这些数据上的性能进行了分析。图3a展示了在每窗口不同波长数量下获得的波图像示例。图3b显示了LFE、k-MDEV、TWENN和ElastoNet在每窗口不同波长数量下，以1 m/s的特定剪切波速（SWS）为基准进行归一化后的预测剪切波速，以及真实值。 当每窗口波长数量＜1时，k-MDEV、LFE、TWENN和ElastoNet的均方根误差（RMSE）分别为0.22、0.25、0.55和0.31 m/s；当每窗口波长数量≥1时，上述四种方法的均方根误差分别为0.01、0.02、0.08和0.01 m/s。尽管当每窗口波长数量＜1时，所有方法的预测值均存在低估情况，但在该范围内，ElastoNet的均方根误差更低，性能优于TWENN。而当每窗口波长数量≥1时，ElastoNet与k-MDEV均表现出最低的均方根误差。 图3b还展示了在ElastoNet上进行的消融研究结果。结果显示，当将单个运动编码梯度（MEG）分量作为输入提供给模型并进行后验平均（而非直接输入所有三个MEG分量）时：当每窗口波长数量＜1时，均方根误差为0.36 m/s（而非0.22 m/s）；当每窗口波长数量≥1时，均方根误差为0.04 m/s（而非0.01 m/s）。 图3c展示了在每窗口2.5个波长的波图像中，不同信号振幅和噪声水平对预测剪切波速、重建误差及不确定性的影响。每窗口0.5至5个波长（以0.5为增量）的波图像结果详见补充材料。

Figure

图

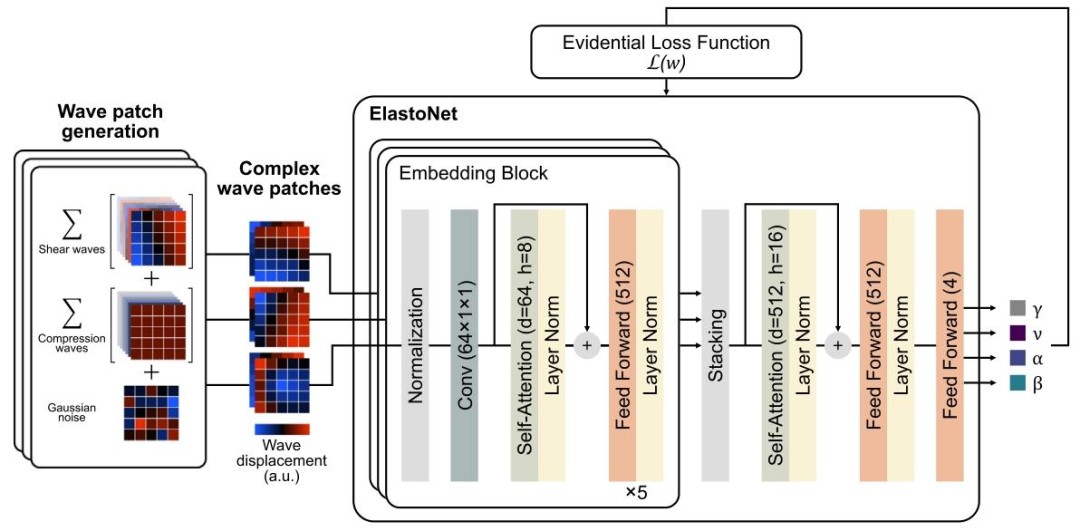
Fig. 1. ElastoNet training. The training data was generated on the fly; the synthetic waves were the superposition of shear waves, compression waves, and Gaussian noise. Forthe neural network training, three complex-valued image wave displacement patches of 5 × 5 pixels were passed as input, and the output consisted of the four parameters of theevidential distribution (𝛾, 𝜈, 𝛼, and 𝛽).

图1. ElastoNet的训练过程   训练数据是动态生成的，合成波由剪切波、压缩波和高斯噪声叠加而成。   在神经网络训练中，输入为3个5×5像素的复数值图像波位移块，输出为证据分布的四个参数（(\gamma)、(\nu)、(\alpha)和(\beta)）。

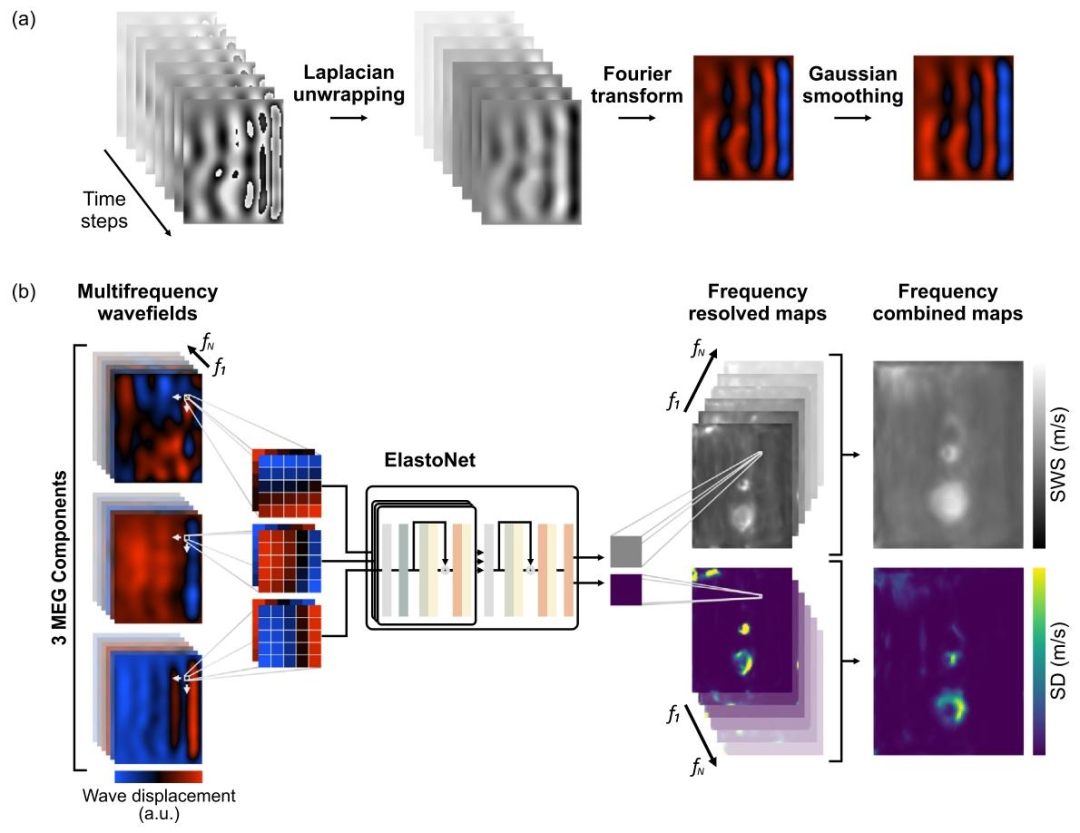
Fig. 2. ElastoNet inference. (a) Pre-processing workflow: for each MEG (motion-encoding gradient) component and vibration frequency, Laplacian unwrapping, Fourier transform,bin selection, and Gaussian smoothing were performed successively. (b) Inference: for each vibration frequency, 3 MEG component images were combined as input to the model,which provided as output a measure of stiffness and its corresponding uncertainty. These were averaged to obtain the final stiffness and uncertainty maps measured through theSWS (shear wave speed) and the corresponding standard deviation (SD)

图2. ElastoNet的推理过程   （a）预处理流程：针对每个运动编码梯度（MEG）分量和振动频率，依次执行拉普拉斯解缠、傅里叶变换、区间选择和高斯平滑。   （b）推理过程：针对每个振动频率，将3个MEG分量图像组合作为模型输入，模型输出刚度度量及其相应的不确定性。对这些结果进行平均，得到通过剪切波速（SWS）测量的最终刚度图和不确定性图（以及相应的标准差（SD））。

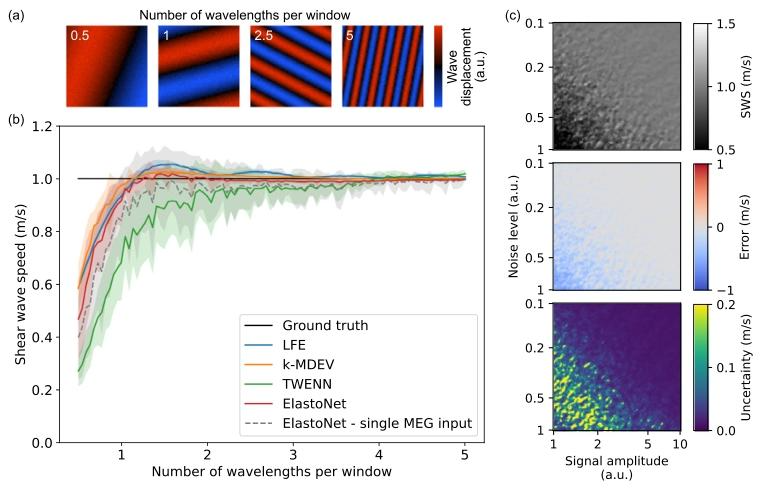
Fig. 3. (a) Examples of synthetically generated plane wave images for 0.5, 1, 2.5, and5 wavelengths per window. (b) Comparison of the ground truth and predicted SWS(shear wave speed) by k-MDEV, LFE, TWENN, and ElastoNet for different numbers ofwavelengths per window, normalized for a SWS of 1 m/s for synthetically generatedplane wave images. The comparison includes, additionally, the result of the ablationstudy performed on ElastoNet, where each MEG (motion-encoding gradient) componentwas provided separately to the model with posterior averaging instead of all three MEGcomponents directly as in ElastoNet. (c) Comparison of the SWS, error, and uncertaintyacross noise level and signal amplitude at 2.5 wavelengths per window

图3   （a）每窗口分别为0.5、1、2.5和5个波长的合成生成平面波图像示例。   （b）在合成生成的平面波图像中，针对每窗口不同波长数量，将k-MDEV、LFE、TWENN和ElastoNet预测的剪切波速（SWS）与真实值进行对比（以1 m/s的SWS为基准进行归一化）。此外，对比还包含在ElastoNet上开展的消融研究结果——该研究中，模型输入为单个运动编码梯度（MEG）分量并进行后验平均，而非像ElastoNet原方法那样直接输入全部三个MEG分量。   （c）在每窗口2.5个波长的条件下，对比不同噪声水平和信号振幅下的剪切波速（SWS）、重建误差及不确定性。

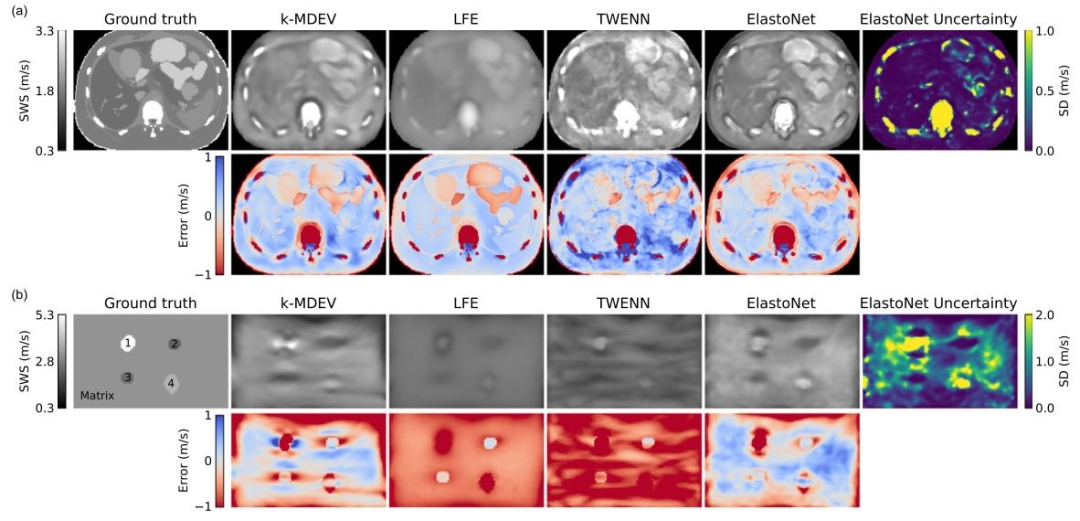
Fig. 4.Comparison of SWS (shear wave speed) maps produced using k-MDEV, LFE, TWENN, and ElastoNet with the ground truth (left), the uncertainty map produced by ElastoNet(right), and the error maps for each of the four SWS maps relative to the ground truth. Maps are displayed in (a) for the FEM (finite element modeling) dataset of a humanabdomen and in (b) for the phantom dataset, where the ground truth image includes the labeling of the four cylindrical inclusions and the matrix of varying SWS (1: 5.94 m/s,2: 2.21 m/s, 3: 2.38 m/s, 4: 3.8 m/s, Matrix: 3.18 m/s). A mask is applied to the images in (a) to suppress the air-filled regions for visualization.

图4  对比了k-MDEV、LFE、TWENN和ElastoNet生成的剪切波速（SWS）图与真实值（左侧），以及ElastoNet生成的不确定性图（右侧），并展示了四个SWS图各自相对于真实值的误差图。   - （a）为人体腹部的有限元模型（FEM）数据集的图像，为便于可视化，已对图像施加掩码以屏蔽含气区域。   - （b）为体模数据集的图像，其中真实值图像标注了四个圆柱形内含物及不同SWS的基质（1：5.94 m/s，2：2.21 m/s，3：2.38 m/s，4：3.8 m/s，基质：3.18 m/s）。

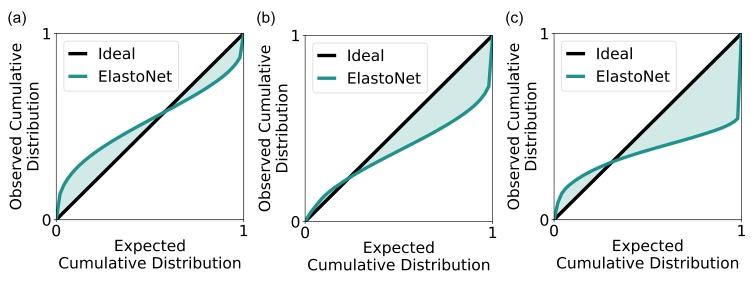
Fig. 5. Calibration curve of the uncertainty for (a) the synthetic plane wave dataset,(b) the FEM (finite element modeling) dataset, and (c) the phantom dataset. Themiscalibration areas for each dataset are (a) 0.09, (b) 0.12, and (c) 0.17 respectively.

图5. 不确定性的校准曲线  （a）合成平面波数据集、（b）有限元模型（FEM）数据集、（c）体模数据集的不确定性校准曲线。各数据集的校准误差面积分别为：（a）0.09、（b）0.12、（c）0.17。

Fig. 6. Comparison of SWS (shear wave speed) maps of the abdomen of a healthy volunteer produced by k-MDEV, LFE, TWENN, and ElastoNet. The magnitude image (left) showsthe segmentations of the regions of interest: the liver outlined in blue, and the spleen outlined in orange. The corresponding uncertainty map produced by ElastoNet is displayeon the right. A mask is applied to the images to suppress the air-filled regions for visualization

图6. 健康志愿者腹部的剪切波速（SWS）图对比**   展示了k-MDEV、LFE、TWENN和ElastoNet生成的健康志愿者腹部剪切波速图。左侧的幅度图像显示了感兴趣区域的分割结果：蓝色轮廓标注的肝脏和橙色轮廓标注的脾脏。右侧为ElastoNet生成的相应不确定性图。为便于可视化，图像已施加掩码以屏蔽含气区域。

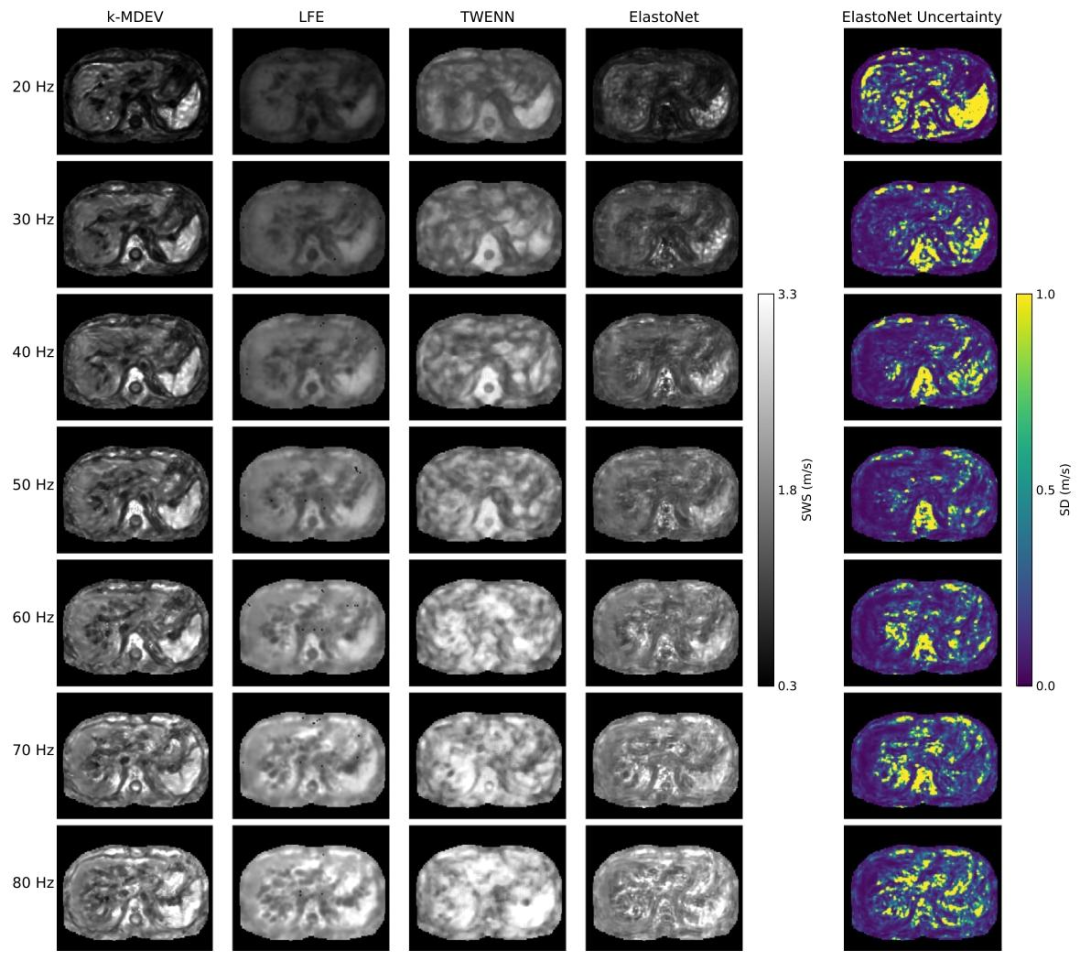
Fig. 7. Comparison of frequency-resolved SWS (shear wave speed) maps of the abdomen of a healthy volunteer produced by k-MDEV, LFE, TWENN, and ElastoNet over a frequencyrange of 20 to 80 Hz. The corresponding frequency-resolved uncertainty maps produced by ElastoNet are displayed on the right. A mask is applied to the images to suppress theair-filled regions for visualization.

图7. 健康志愿者腹部的频率分辨剪切波速（SWS）图对比   展示了k-MDEV、LFE、TWENN和ElastoNet在20至80 Hz频率范围内生成的健康志愿者腹部频率分辨剪切波速图。右侧为ElastoNet生成的相应频率分辨不确定性图。为便于可视化，图像已施加掩码以屏蔽含气区域。

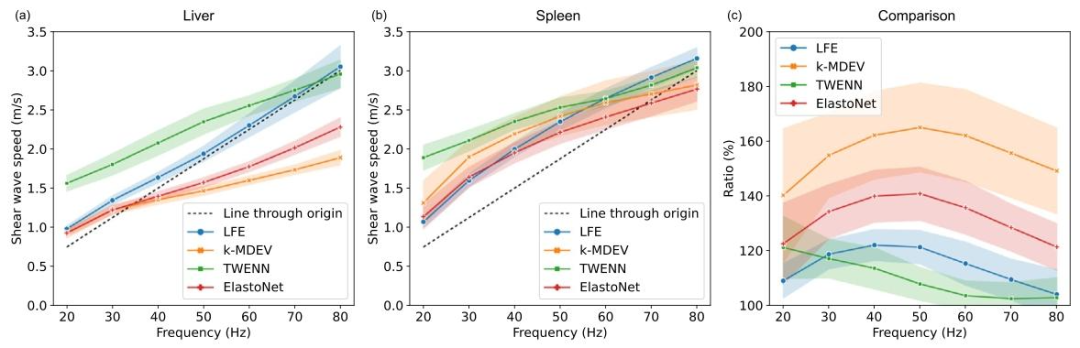
Fig. 8. Dispersion curves of (a) the liver, (b) the spleen, and (c) the ratio between the SWS (shear wave speed) of the spleen and the liver for LFE (blue), k-MDEV (orange),TWENN (green), and ElastoNet (red) including the mean and the standard deviation at each frequency for the abdominal imaging dataset acquired in 14 healthy volunteers. Thedashed line in (a) and (b) indicates a constant proportionality of SWS and frequency, which is only the case if the predicted wavelength does not change with frequency as anartifact of geometry

图8. 色散曲线   （a）肝脏、（b）脾脏的色散曲线，以及（c）14名健康志愿者腹部成像数据集中，LFE（蓝色）、k-MDEV（橙色）、TWENN（绿色）和ElastoNet（红色）所测脾脏与肝脏剪切波速（SWS）的比值曲线，包含各频率下的均值和标准差。   （a）和（b）中的虚线表示剪切波速与频率呈恒定比例关系，这种情况仅当预测波长不随频率变化（属于几何伪影）时出现。   （注：色散曲线用于描述剪切波速随频率的变化关系，可反映组织的粘弹性特性；不同方法的曲线差异体现了各自对频率依赖性的捕捉能力。）

Table

表

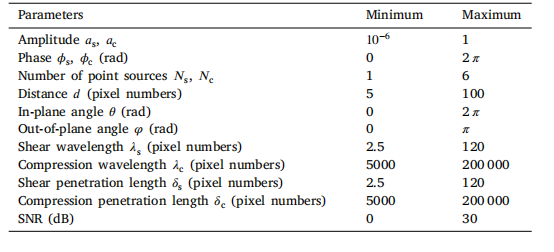
Table 1Parameters of the model used to generate the training wave displacement images

表1   用于生成训练波位移图像的模型参数

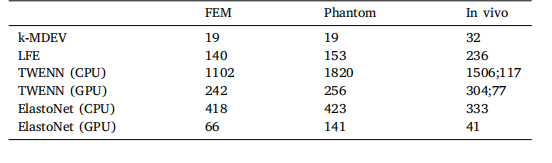
Table 2Reconstruction times in seconds for k-MDEV, LFE, TWENN and ElastoNet for the FEM(finite element modeling), phantom, and in vivo datasets. For the in vivo dataset, theresults are reported per dataset. For TWENN we report for the in vivo dataset the timenecessary for the first dataset and for every subsequent case

表2   k-MDEV、LFE、TWENN和ElastoNet在有限元模型（FEM）、体模和在体数据集上的重建时间（以秒为单位）。对于在体数据集，结果按每个数据集单独报告。对于TWENN，在体数据集的重建时间分别报告了第一个数据集的耗时以及后续每个案例的耗时。

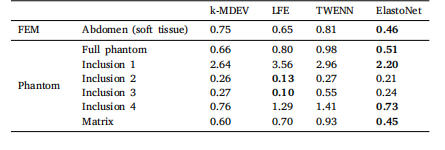
Table 3Root mean square error (m/s) of the SWS (shear wave speed) maps produced byElastoNet, LFE, TWENN, and k-MDEV relative to the ground truth for the FEM (finiteelement modeling) and phantom datasets in the following regions of interest: the fullabdomen excluding bone structures in the FEM abdomen dataset, the full phantom andeach of the four inclusions of varying SWS and the matrix in the phantom dataset.

表3   ElastoNet、LFE、TWENN和k-MDEV生成的剪切波速（SWS）图相对于真实值的均方根误差（单位：m/s），评估对象包括有限元模型（FEM）数据集和体模数据集的以下感兴趣区域：   - 有限元腹部数据集中，排除骨骼结构的整个腹部区域；   - 体模数据集中，整个体模、四个不同剪切波速的内含物以及基质。