当前位置：首页 > news >正文

【数据结构与算法】数据结构初阶：详解二叉树（六）——二叉树应用：二叉树选择题

news 2025/7/26 5:10:09

🔥个人主页：艾莉丝努力练剑

❄专栏传送门：《C语言》、《数据结构与算法》、C语言刷题12天IO强训、LeetCode代码强化刷题

🍉学习方向：C/C++方向

⭐️人生格言：为天地立心，为生民立命，为往圣继绝学，为万世开太平

重要提醒：为什么我们要学那么多的数据结构？这是因为没有一种数据结构能够去应对所有场景。我们在不同的场景需要选择不同的数据结构，所以数据结构没有谁好谁坏之分，而评估数据结构的好坏要针对场景，如果在一种场景下我们需要频繁地对头部进行插入删除操作，那么这个时候我们用链表；但是如果对尾部进行插入删除操作比较频繁，那我们用顺序表比较好。

因此，不同的场景我们选择不同的数据结构。

前言：本篇文章，我们继续来看二叉树，来刷一刷选择题，其实也是对前面学过的知识的一个回顾与练习，毕竟笔试面试已经越来越看重程序员的算法能力，把选择题作为一个对已学知识的一个快速回顾——比如说加深对数据结构某个重要性质的记忆、降低记忆成本——还是很值得去做的。我们做这些选择题正有此意：一来加深了对二叉树性质的理解；二来通过做几道代表性的选择题我们将知识点迅速运用了起来，让知识顺利扎根在大脑；三来也是对自己学习二叉树学习情况的一个小测验。

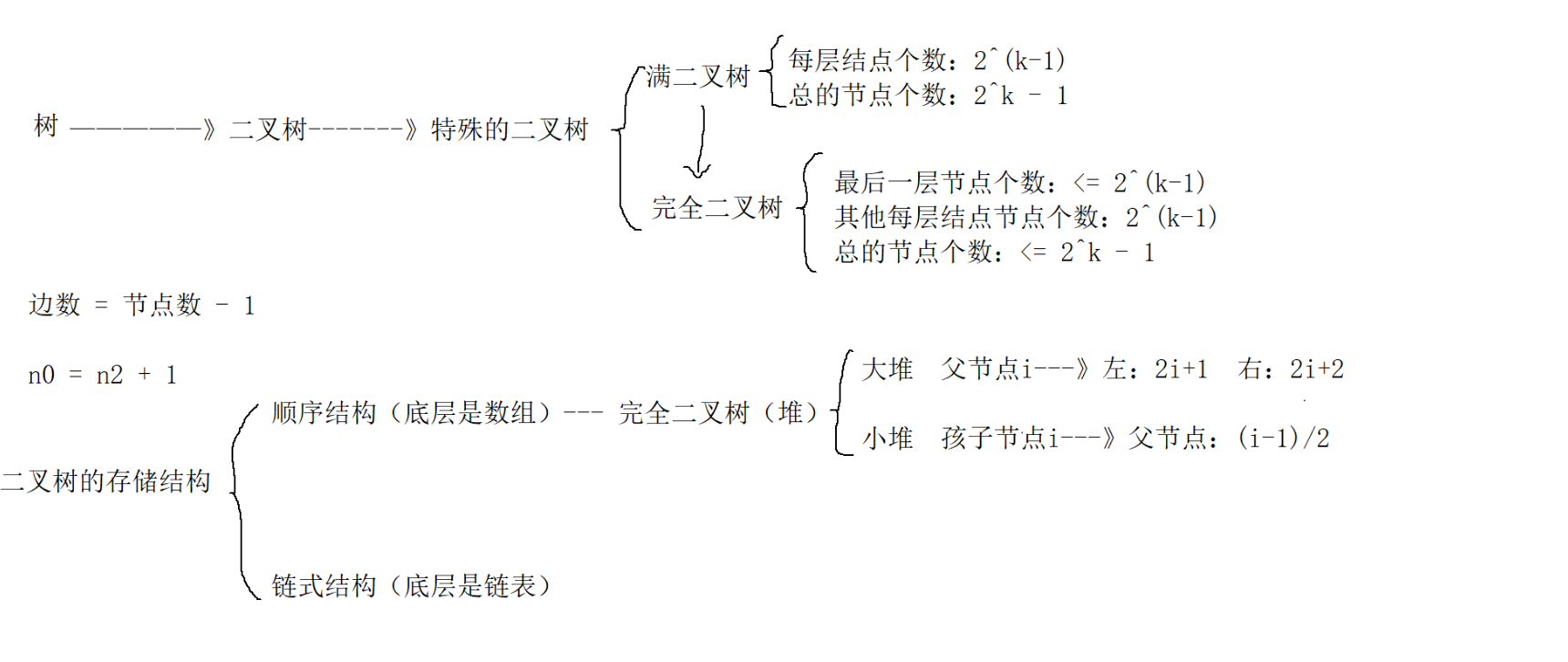
正文

一、二叉树性质相关选择题

（一）性质

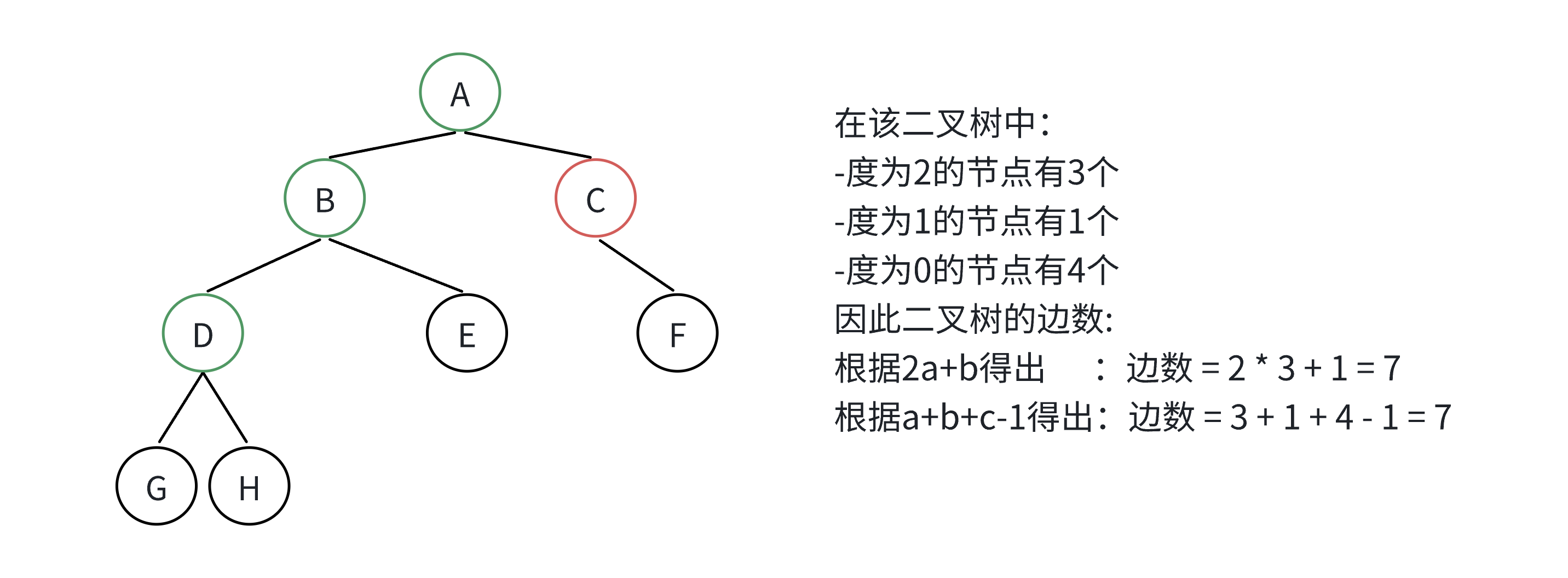
证明：

假设一个二叉树有 a 个度为2的节点，b 个度为1的节点，c 个叶节点，则这个二叉树的边数是 2a+b，另一方面，由于共有 a+b+c 个节点，所以边数等于 a+b+c-1。

2a + b = a + b + c - 1 ，即： a = c-1。

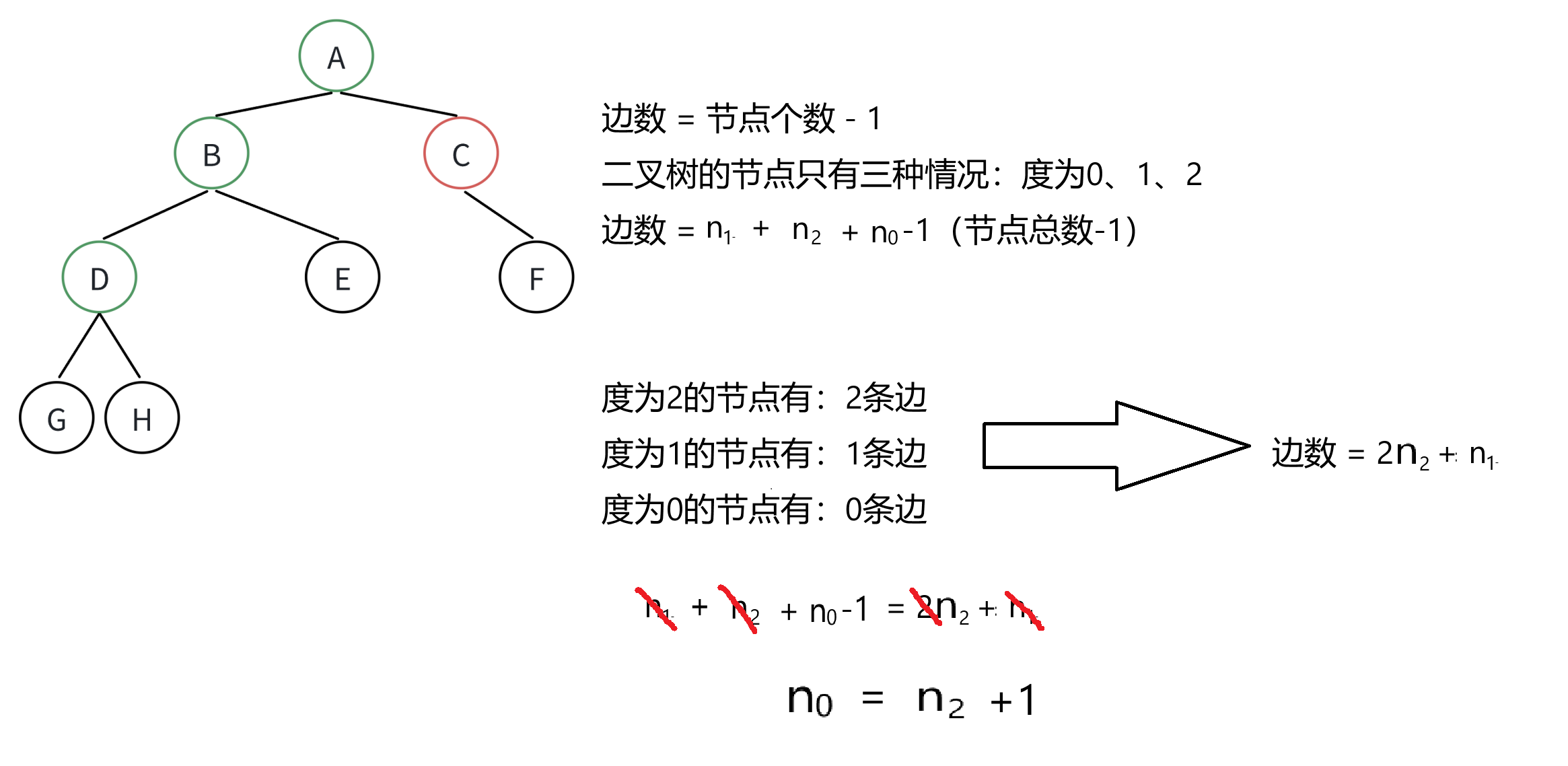
（二）题目

1、题目1

1、某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（）

A 不存在这样的二叉树

B 200

C 198

D 199

解析：

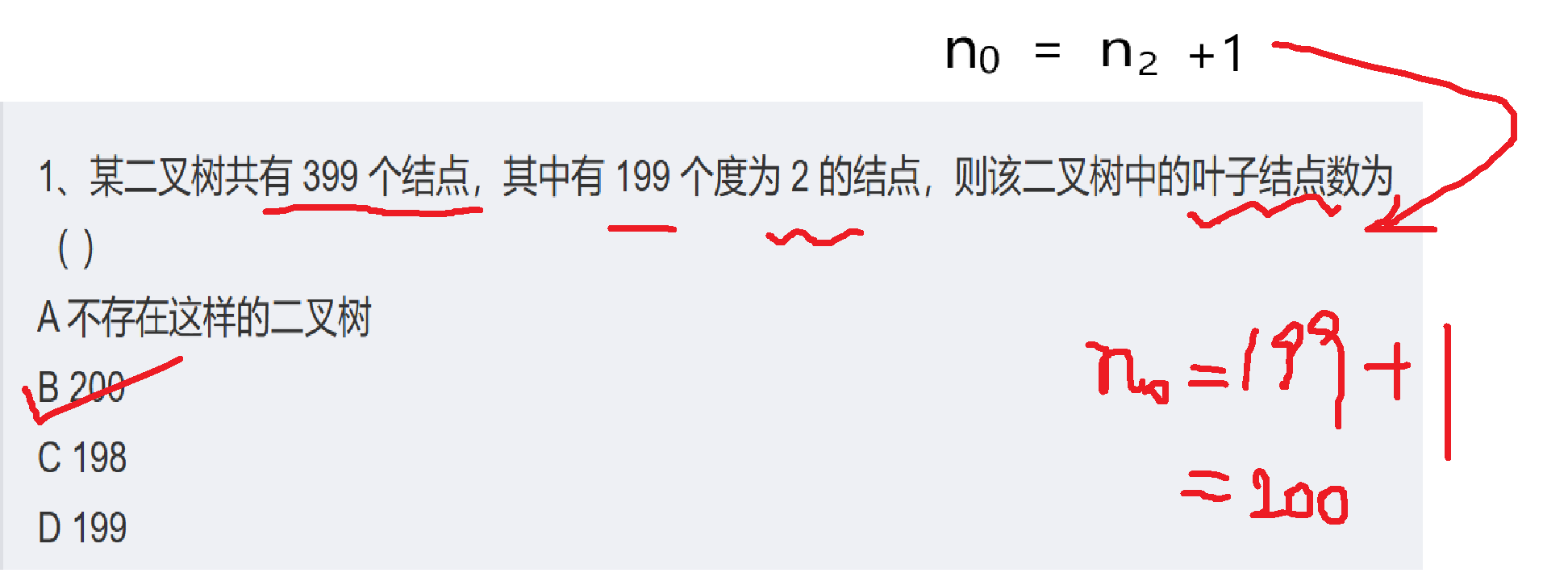
2、题目2

2、在具有 2n 个结点的完全二叉树中，叶子结点个数为（）

A n

B n+1

C n-1

D n / 2

解析：

在完全二叉树，有多少度为1的节点个数

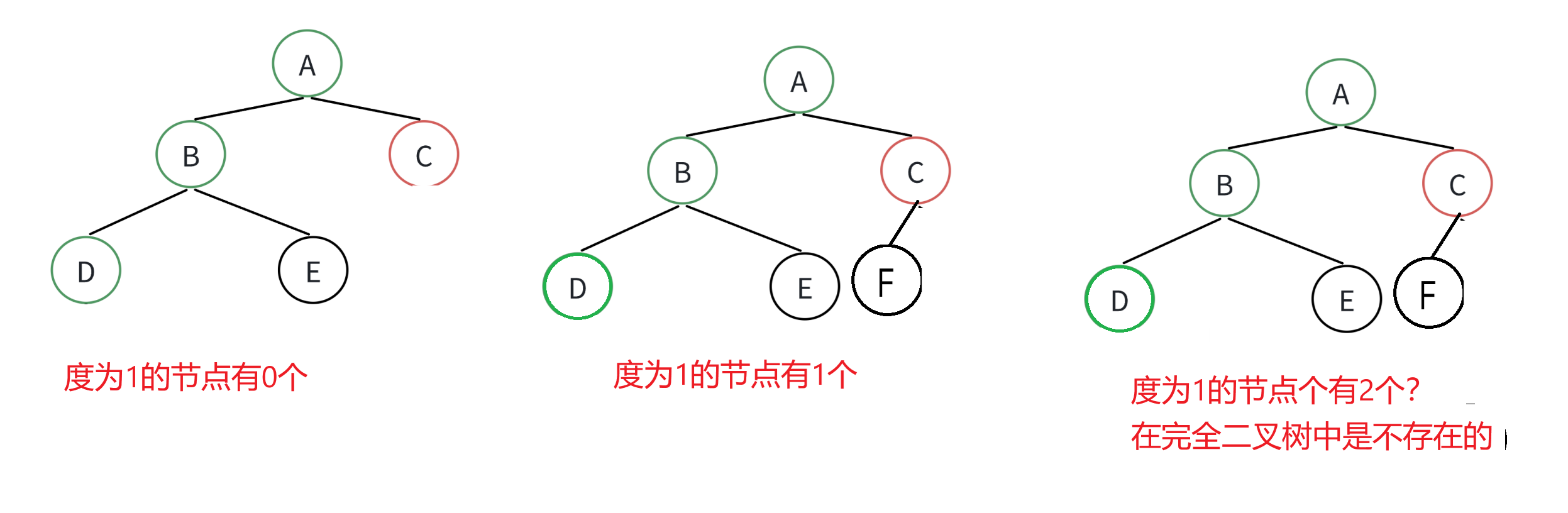
3、题目3

3、一棵完全二叉树的结点数位为531个，那么这棵树的高度为（）

A 11

B 10

C 8

D 12

解析：

4、题目4

4、一个具有767个结点的完全二叉树，其叶子结点个数为（）

A 383

B 384

C 385

D 386

解析：

二叉树性质相关选择题答案：

1、B

2、A

3、B

4、B

二、链式二叉树遍历相关选择题

1、题目1

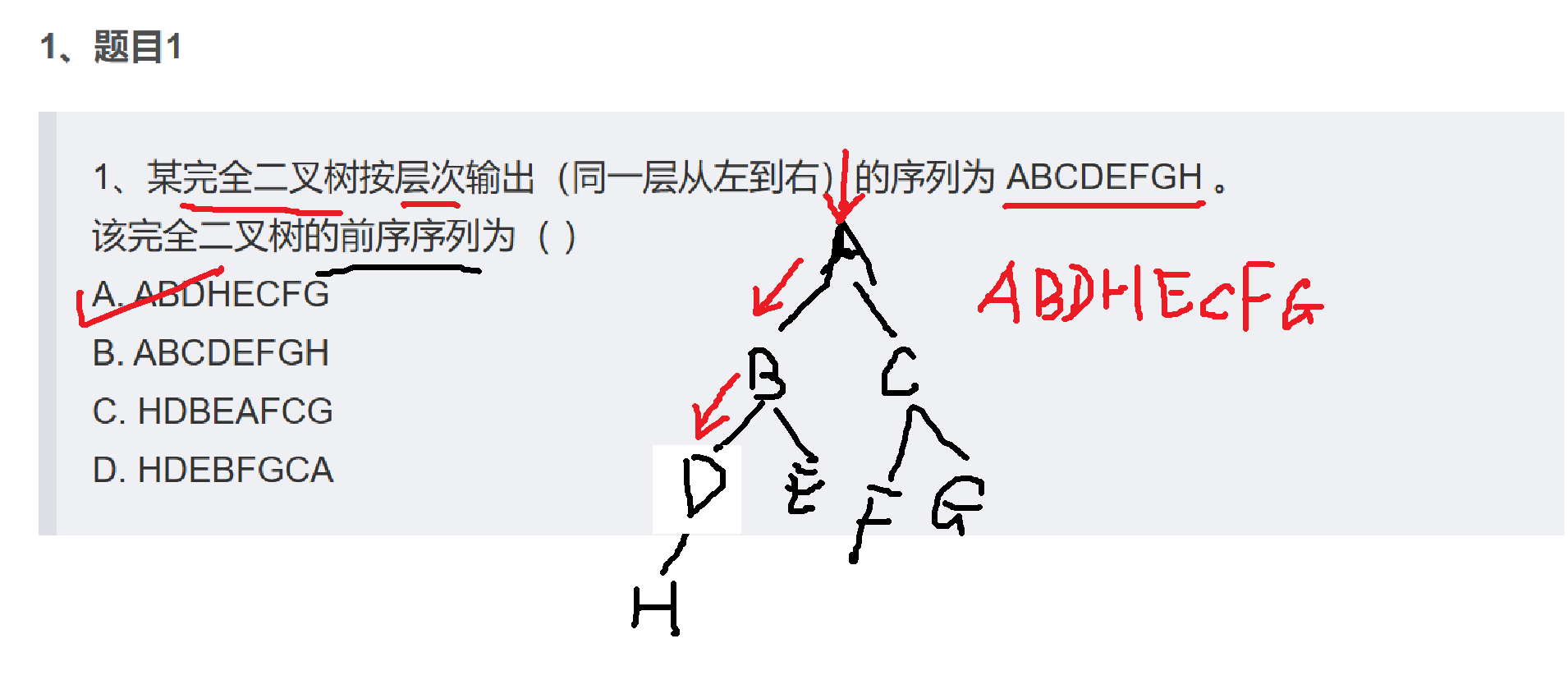
1、某完全二叉树按层次输出（同一层从左到右）的序列为 ABCDEFGH 。

该完全二叉树的前序序列为（）

A. ABDHECFG

B. ABCDEFGH

C. HDBEAFCG

D. HDEBFGCA

解析：

2、题目2

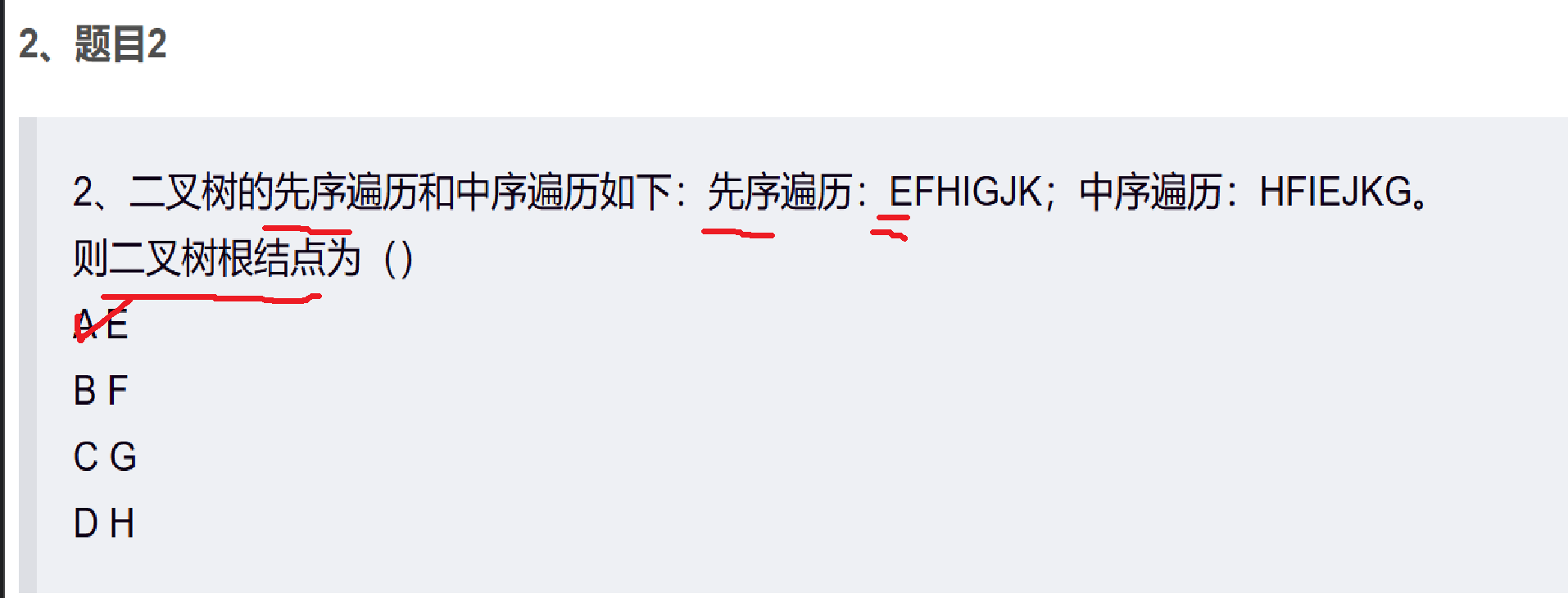
2、二叉树的先序遍历和中序遍历如下：先序遍历：EFHIGJK；中序遍历：HFIEJKG。

则二叉树根结点为（）

A E

B F

C G

D H

解析：先序遍历打印的一个是就是根节点，知道了先序遍历，根节点就找到了。

3、题目3

3、设一课二叉树的中序遍历序列：badce，后序遍历序列：bdeca，

则二叉树前序遍历序列为____。

A adbce

B decab

C debac

D abcde

解析：

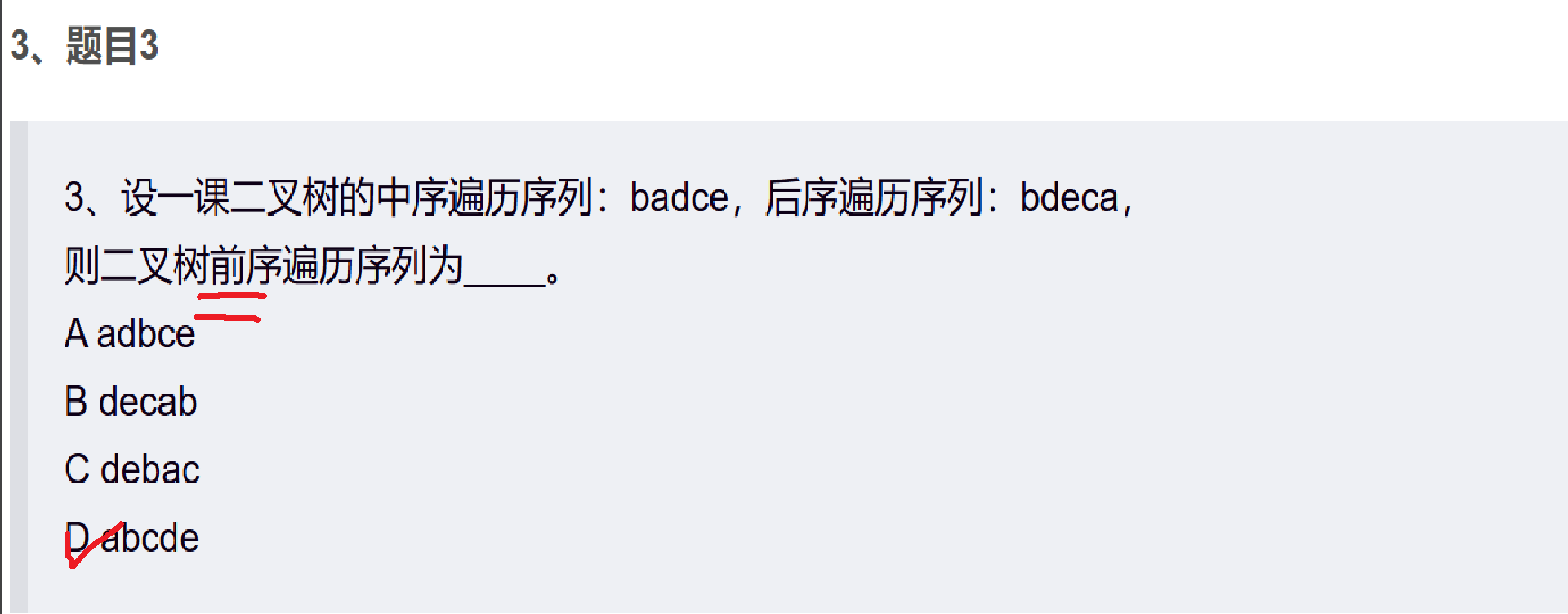
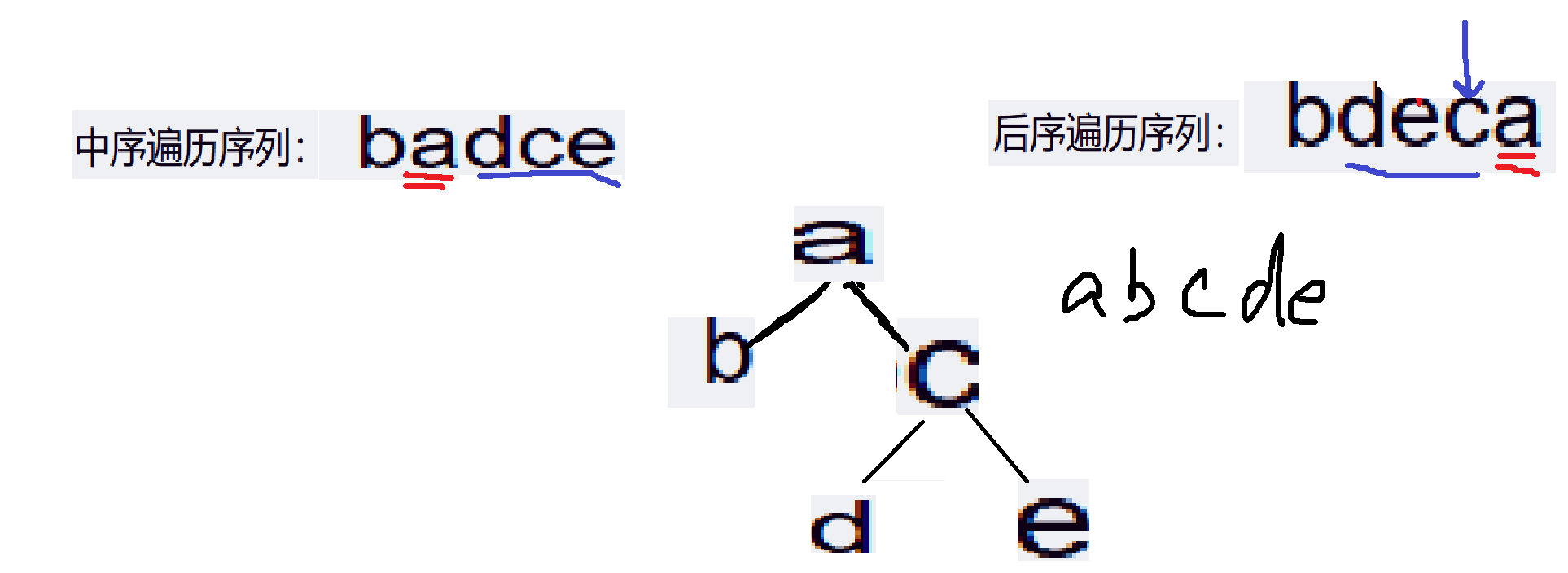
方法： 确定一个删掉一个，也就是说：已知任意两个求第三个。

根据后序遍历找到根节点，中序遍历看左右孩子。如下图：

1、根据后序遍历我们确定根节点就是a：

2、确定了，我们就把它删掉，以免对我们产生干扰：

3、确定了a是根节点，我们看一下中序遍历，a的左子树是b，确定的就删掉：

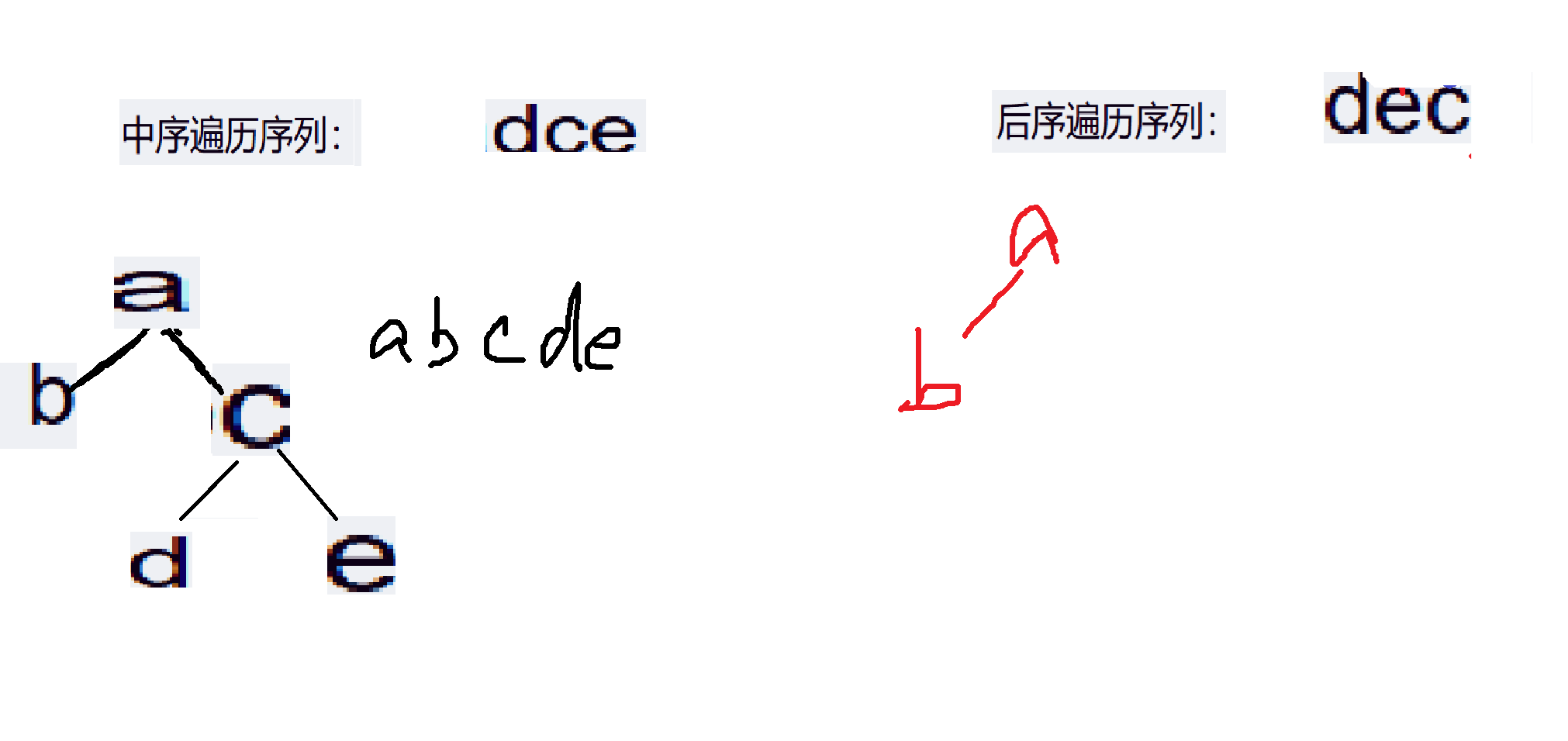
4、我们看：a的右子树，中序遍历的结果是dce，后序遍历的结果是dec，ab我们都删掉了，没有干扰项。dec，根节点是c，既然根节点是c，我们再回到中序遍历，c的左子树是d，c的右子树是e。后面大家做这种题目就可以采用这种方法。

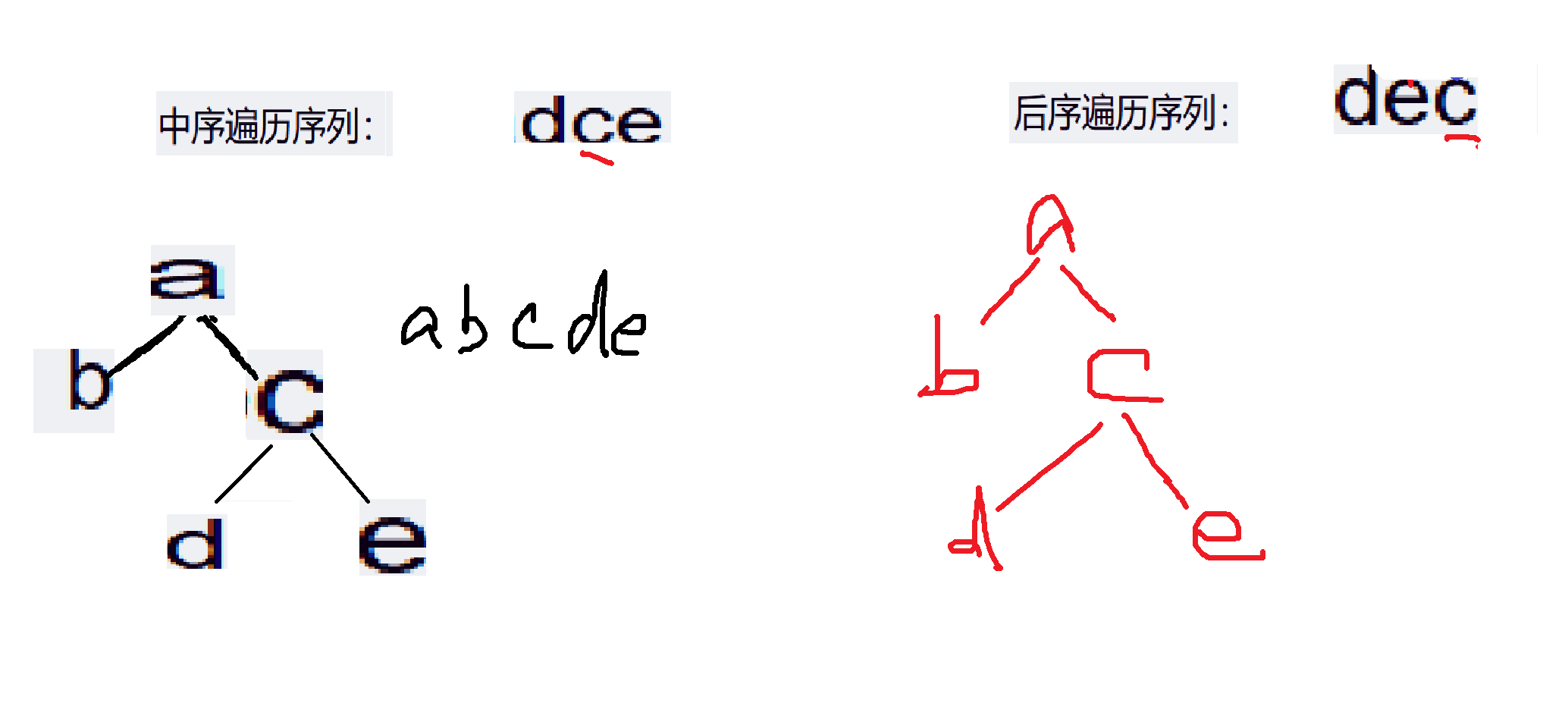
4、题目4

4、某二叉树的后序遍历序列与中序遍历序列相同，均为 ABCDEF，则按层次输出（同一层从左到右）的序列为（）

A FEDCBA

B CBAFED

C DEFCBA

D ABCDEF

解析：

只有左子树，没有右子树。

5、加餐1：题目5

5、已知某二叉树的中序遍历序列为JGDHKBAELIMCF，后序遍历序列为JGKHDBLMIEFCA，则其前序遍历序列为（）

A.ABDGHJKCEFILM

B.ABDGJHKCEILMF

C.ABDHKGJCEILMF

D.ABDGJHKCEIMLF

解析：

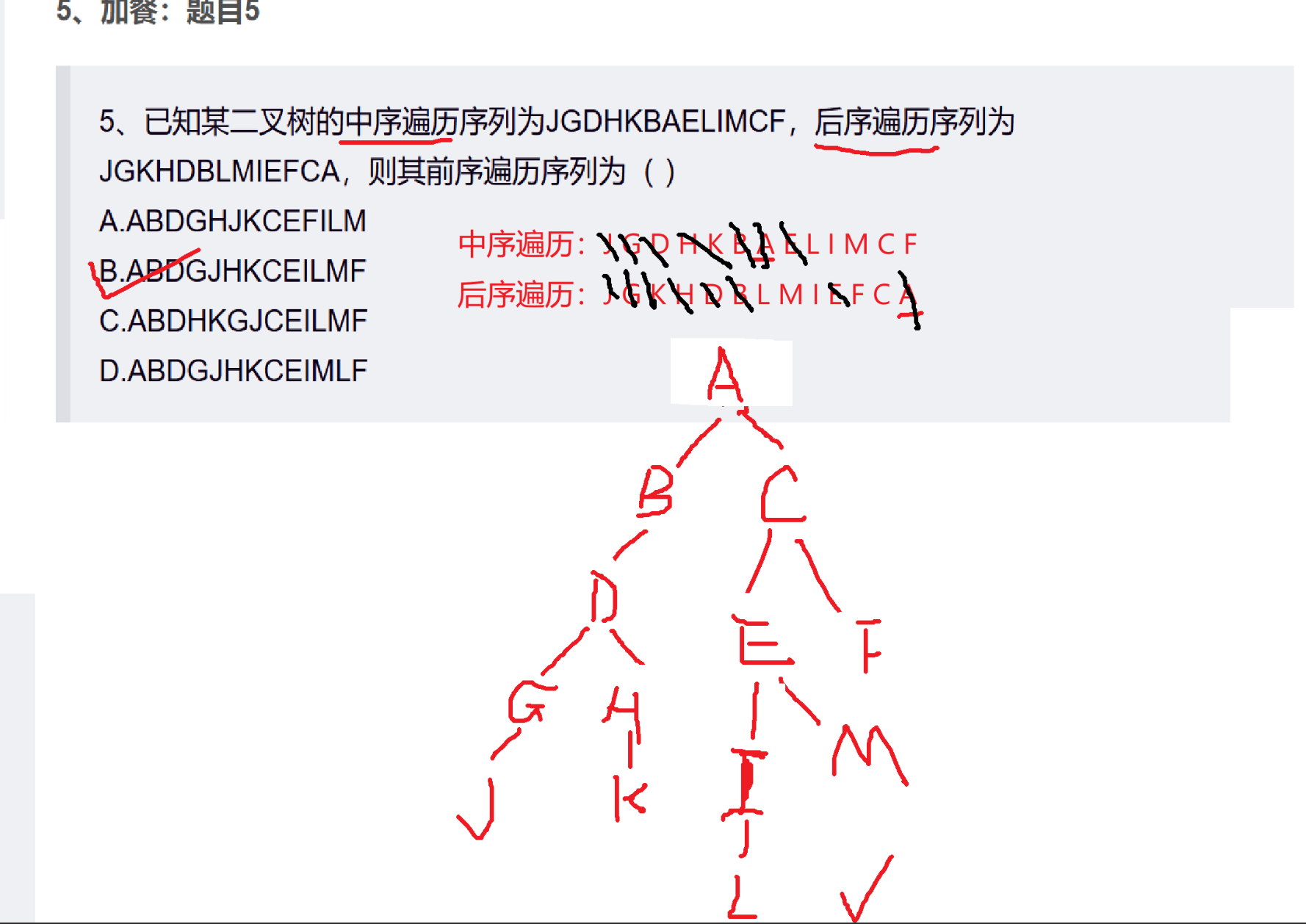
由后序遍历确定子树的根，后序遍历从后向前看，最后一个元素为根，和前序遍历刚好相反，从后向前看后序遍历，应该是根，右，左，根据中序遍历确定子树的左右区间。

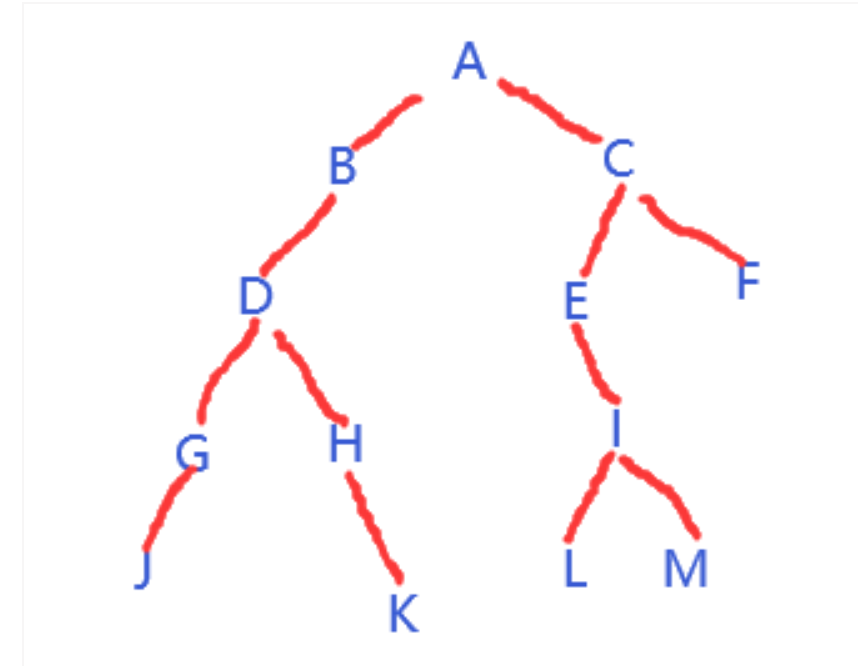
详解：

我们根据后序遍历可知，A是根节点——

A的左子树：JGDHKB，A的右子树：ELIMCF；

A的左子树的根：B，A的右子树的根：C；

B的左子树：JGDHK，B的右子树：空，C的左子树：ELIM，C的右子树：F；

B的左子树的根：D，C的左子树根：E；

D的左子树的根：G，D的右子树的根：H，E的右子树的根：I。

6、加餐2：题目6

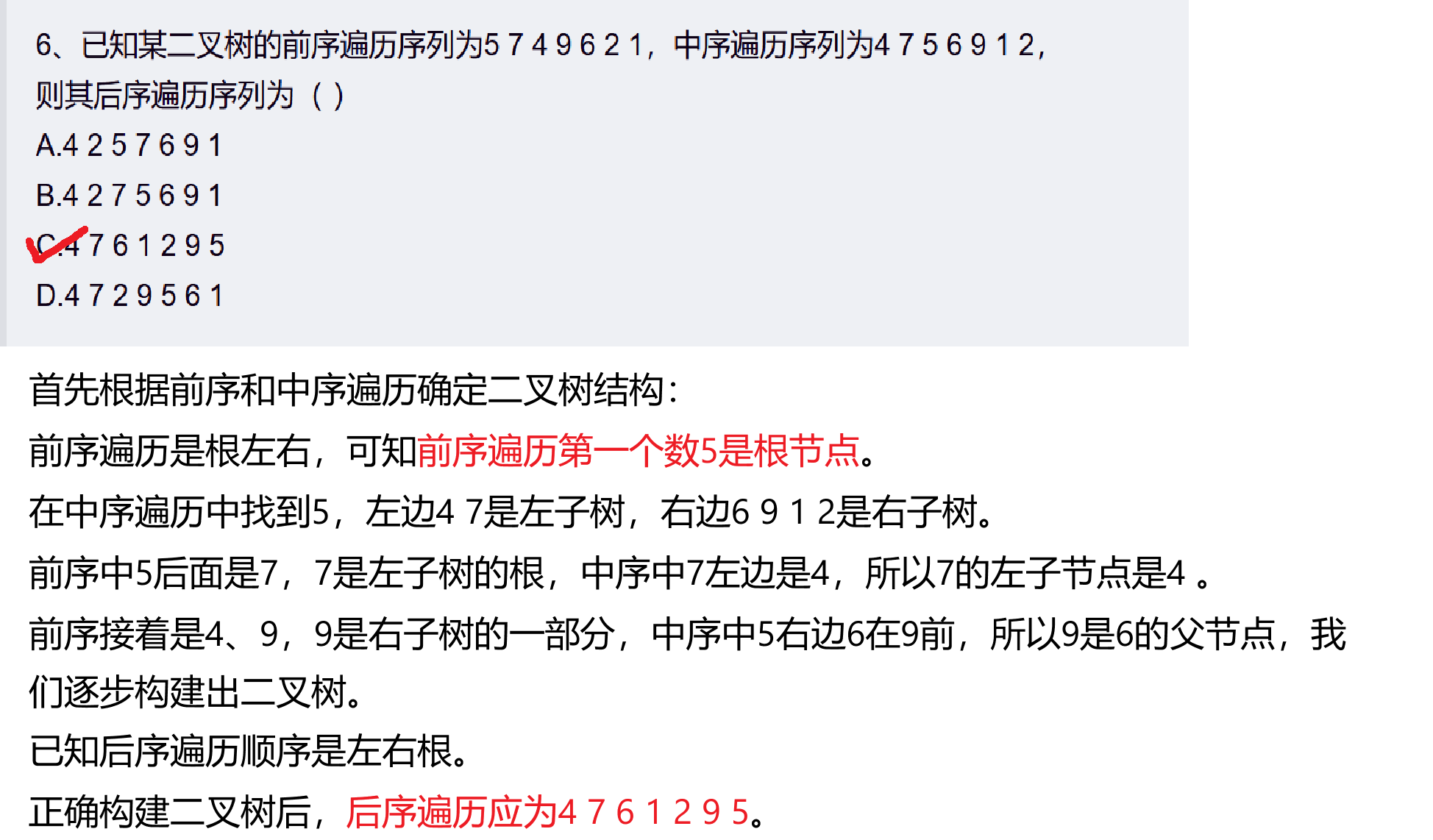
6、已知某二叉树的前序遍历序列为5 7 4 9 6 2 1，中序遍历序列为4 7 5 6 9 1 2，

则其后序遍历序列为（）

A.4 2 5 7 6 9 1

B.4 2 7 5 6 9 1

C.4 7 6 1 2 9 5

D.4 7 2 9 5 6 1

解析：

首先根据前序和中序遍历确定二叉树结构：
前序遍历是根左右，可知前序遍历第一个数5是根节点。
在中序遍历中找到5，左边4 7是左子树，右边6 9 1 2是右子树。
前序中5后面是7，7是左子树的根，中序中7左边是4，所以7的左子节点是4 。
前序接着是4、9，9是右子树的一部分，中序中5右边6在9前，所以9是6的父节点，我们逐步构建出二叉树。
已知后序遍历顺序是左右根。
正确构建二叉树后，后序遍历应为4 7 6 1 2 9 5。

链式二叉树遍历相关选择题答案：

1、A

2、A

3、D

4、A

5、B

6、C

三、二叉树树度相关选择题

1、题目1

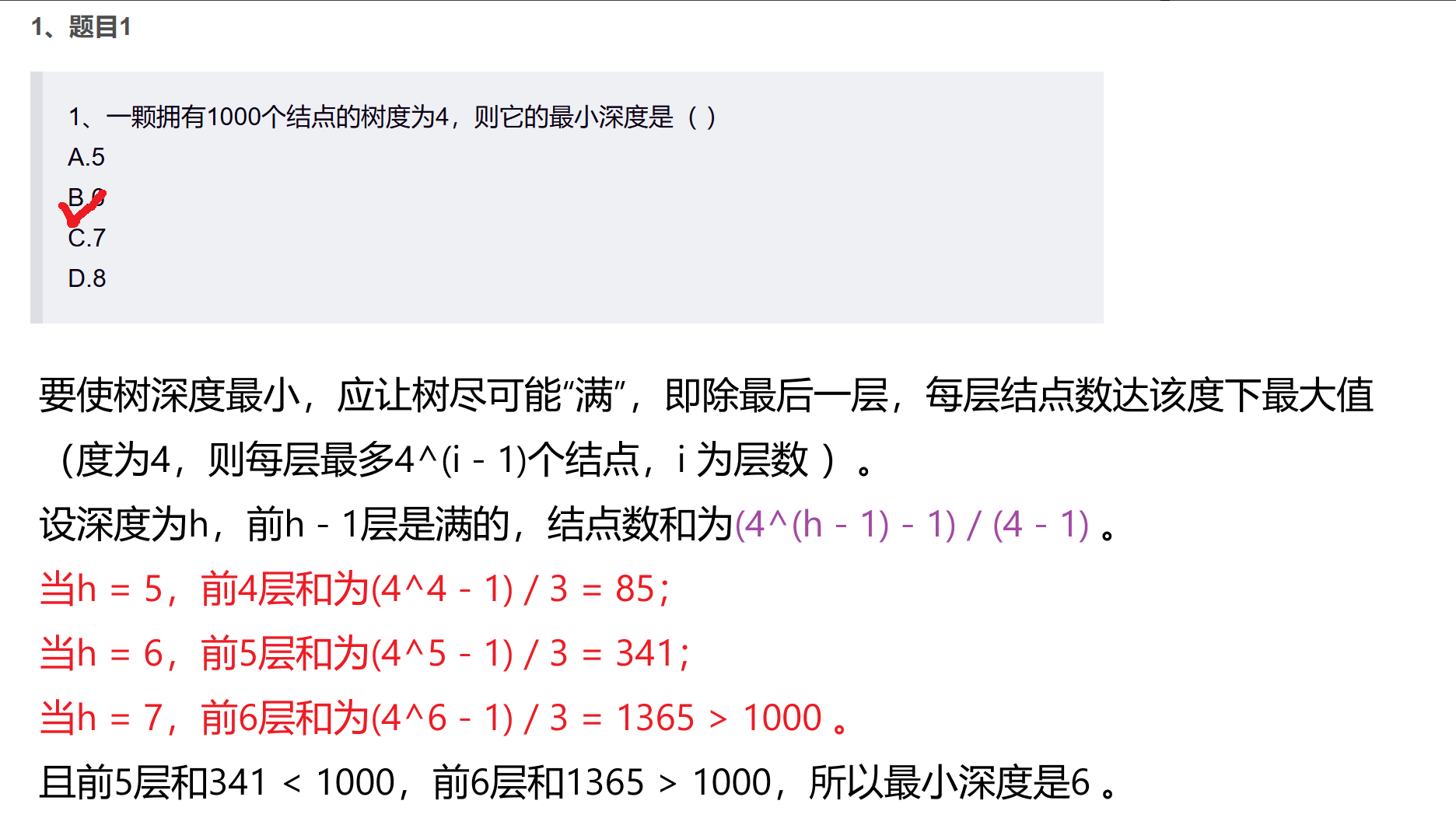
1、一颗拥有1000个结点的树度为4，则它的最小深度是（）

A.5

B.6

C.7

D.8

解析·：

要使树深度最小，应让树尽可能“满”，即除最后一层，每层结点数达该度下最大值

（度为4，则每层最多4^(i - 1)个结点，i 为层数）。
设深度为h，前h - 1层是满的，结点数和为(4^(h - 1) - 1) / (4 - 1) 。
当h = 5，前4层和为(4^4 - 1) / 3 = 85；

当h = 6，前5层和为(4^5 - 1) / 3 = 341；

当h = 7，前6层和为(4^6 - 1) / 3 = 1365 > 1000 。
且前5层和341 < 1000，前6层和1365 > 1000，所以最小深度是6 。