【初识数据结构】CS61B 中的归并排序和选择排序
本教程介绍 归并排序和插入排序
归并排序
设想
首先我们设想一个情景,如果我们有两个已排序的数组,现在我们要把这两个数组进行合并成一个有序的大数组,应该需要多少的时间复杂度?
答案是O(N)O(N)O(N)!
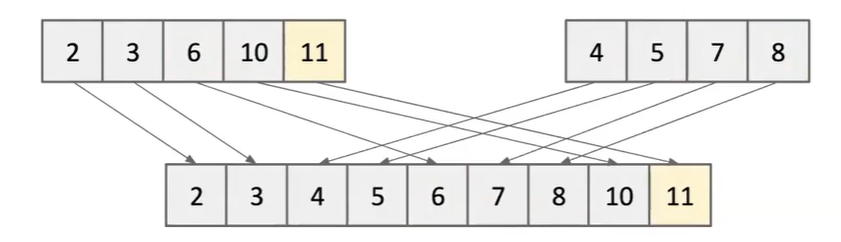
我们每次取两数组中最小的那个进行比较,然后把较小者放入合并后的数组即可
分析
我们知道选择排序的时间复杂度为 O(N2)O(N^2)O(N2) ,我们现在以 N=64N=64N=64 的数组进行分析,如果我们直接对它进行选择排序,那我们消耗的时间为:642=409664^2=4096642=4096
那我们如果对他进行一次归并呢,也就是把他化为两个小数组,分别排序再合并
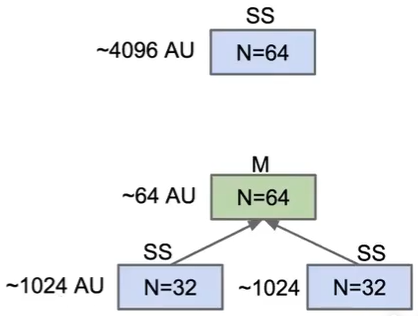
我们会发现,原本 N2N^2N2 的时间,变为了 N+2∗(N/2)2=N+N2/2N+2*(N/2)^2=N+N^2/2N+2∗(N/2)2=N+N2/2
虽然这看起来仍然是平方的时间复杂度,但是因为 N+N2/2<N2N+N^2/2<N^2N+N2/2<N2,所以我们的时间还是变快了
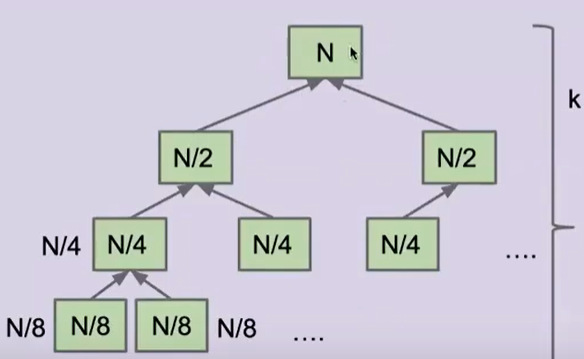
不断地归并
现在我们通过初步的分析知道,通过归并可以让时间变短,那如果我就这样贪婪地不断进行归并呢?
我们对原本的数组不断进行归并,直到无法再归并了,也就是基本情况,现在我们再来分析一下所需的时间是多少
我们会发现除了最后一层以外,上面的每一层都只需要进行线性操作即可,也就是对两个已经排序的数组进行合并
而最后一层呢?只有一个元素! 也就是不需要进行排序
所以其实我们只需要进行这些合并的线性操作即可!
时间复杂度分析
接下来我们可以看到,第一层为 1∗N1*N1∗N,第二层为 2∗N/22 * N/22∗N/2 ,第三层为 4∗N/44*N/44∗N/4……,我们可以发现每一层的时间都是 NNN
那么一共有多少层呢,这实际上是一个完全二叉树,也就是 logNlogNlogN 层
所以我们可以得出时间复杂度为: θ(NlogN)\theta(NlogN)θ(NlogN)
空间复杂度为 θ(N)\theta(N)θ(N) ,因为我们需要一个额外的N数组,来储存合并后的结果
btw
归并排序是一种非常讲究组织的排序,他会将一个大数组不断地进行分割,再不断进行合并,可能它会具有比较好的并行性能
插入排序
插入排序其实很像我们在构造堆中的“上浮”和“下沉”操作,我们往下看
算法核心
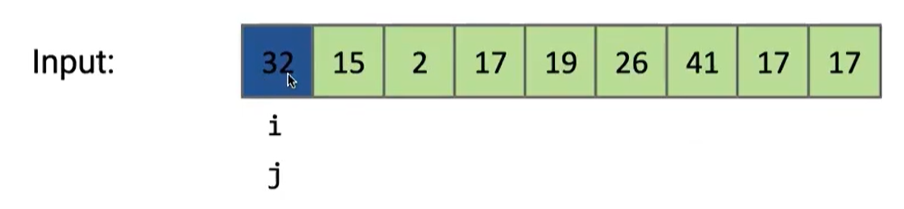
我们以这个插入排序为例,对于未排序的首个元素,这个元素向左看,是否小于该元素:
- 是,则交换
- 否,则放置在这里,然后考虑下一个未排序的元素
算法流程
在这里,第一个元素为32,它左边没有可比较的元素,那他就放在这里
然后考虑15,和 32 比较,小于32?是的,进行交换;左边没有可以比较的,就放在这里
考虑2,小于32?是的,交换;小于15?是的,交换;左边没有元素,放在这里
考虑17,小于32?是的,交换;小于15?否,放在这,考虑下一个
…
类比
插入排序每次取出的元素不像选择排序那样,每次都需要取出最值元素,每次取出的元素没有限制,取出元素后,直接进入已排序的区域然后发生“下沉”,如果发现无法下沉了,这里就一定是他该待的位置了
时间复杂度分析
最好的情况是,我们每次取出一个元素,发现都无需发生“下沉”,也就是每个元素都已经在它该在的位置了,这里时间复杂度为 Ω(N)\Omega(N)Ω(N)
最坏的情况是,每次取出一个元素,都要下沉到底,尽可能地做交换,第一次是0,最后一次是 N-1,这里时间复杂度为 O(N2)O(N^2)O(N2)
优势
插入排序的优势在于,在我的整个数组已经大部分都已排序的情况下,它的表现比其他的算法更好
比如我的整个已排序的数组中有一个数据被篡改了,现在我要重新排序,插入排序的性能表现相较于归并排序或者插入排序就非常棒了