【数据结构】——时间与空间复杂度深度解析

在编程过程中，算法性能是决定程序效率的核心因素。无论是处理海量数据的服务器程序，还是对实时性要求极高的嵌入式系统，时间复杂度和空间复杂度都是衡量算法优劣的关键指标。本篇文章将从基础概念入手，并结合C语言代码示例。

为什么需要复杂度分析？

我们如何衡量一个算法的好坏，在代码运行时需要消耗时间资源和空间资源，所有衡量一个算法的好坏一般是从时间和空间两个维度来衡量的，即时间复杂度和空间复杂度。

---

一. 时间复杂度

• 时间复杂度的定义

时间复杂度衡量算法执行时间随输入规模的增长趋势，用大O符号表示。

• 大O表示法

用 O(f(n)) 描述算法的最坏时间复杂度，其中 f(n) 是算法运行时间的上界。

常见时间复杂度

复杂度	示例算法	增长趋势	适用场景
O(1)	数组索引访问	恒定(常数时间)	快速查找、简单操作
O(log n)	二分查找	缓慢增长(对数时间)	有序数据搜索
O(n)	线性遍历	线性增长(线性时间)	简单遍历、统计
O(n log n)	快速排序、归并排序	亚线性增长(线性对数时间)	高效排序
O(n2)	冒泡排序、选择排序	平方增长(平方时间)	小规模数据排序
O(2n)	递归斐波那契	指数爆炸(指数时间)	避免使用（除非输入极小）

---

---

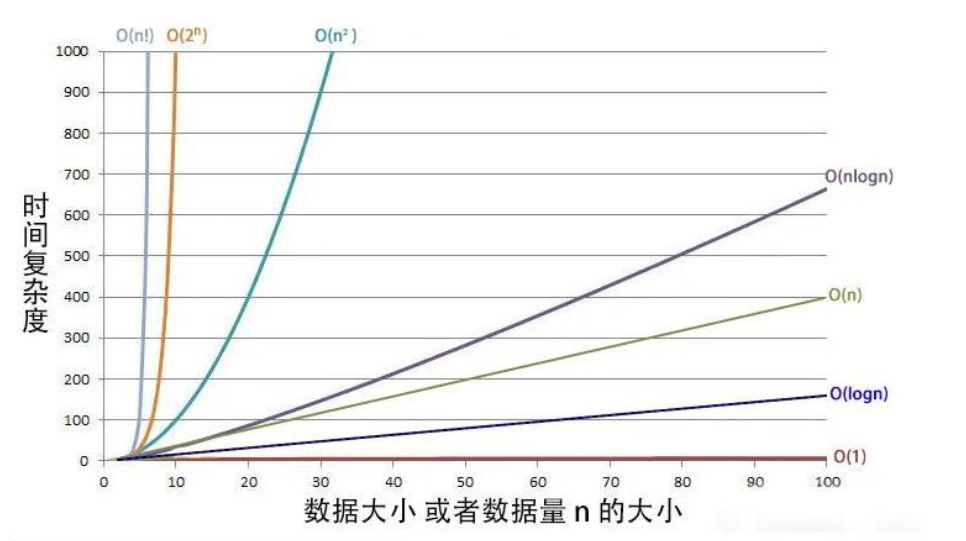
在计算过程中忽略常数系数O(2n) 简化为 O(n)。保留最高阶项O(n² + n) 简化为 (O(n²)。时间复杂度不等于实际运行时间，它仅描述增长趋势。

时间复杂度为：O(1)

void Fun()
{int count = 0;for (int k = 0; k < 100; k++)//N为常数{++count;}printf("%d\n", count);
}

---

时间复杂度为：O(log n)

int binarySearch(int arr[], int left, int right, int target) 
{while (left <= right){int mid = left + (right - left) / 2; // 防止溢出，等同于 (left + right)/2if (arr[mid] == target) return mid; // 找到目标，返回索引else if (arr[mid] < target) left = mid + 1; // 目标在右半部分else right = mid - 1; // 目标在左半部分}return -1; // 未找到
}

---

时间复杂度为：O(n)

// 字符串查找函数
const char* strchr(const char* str, int ch) 
{while(*str) {                  // 最坏情况：遍历整个字符串if(*str == ch) return str;str++;}return NULL;
}
// 时间复杂度：O(n)（最坏情况）

---

时间复杂度为：O(n²)

void fun(int n)
{int count = 0; for(int i = 0;i < n; i++){for(int j = 0;j < n; j++){count++;}}
}

---

时间复杂度为：O(2ⁿ)

long long fib(int n)
{if(n<3)return 1;return Fib(n-1)+Fib(n-2);
}

---

如何优化时间复杂度

• 选择更优的算法
• 减少重复的计算
• 避免多层循环
• 利用时间换取空间

---

二. 空间复杂度

空间复杂度用于衡量算法在运行过程中临时占用存储空间的大小，通常关注的是额外空间（即除输入数据本身外占用的空间）。空间复杂度与时间复杂度类似，用大O符号表示，描述空间需求随输入规模 n 的增长趋势。

常见空间复杂度

复杂度	名称	示例算法/操作
O(1)	常数空间	迭代计算、原地排序（如冒泡排序）
O(n)	线性空间	动态数组、哈希表、递归栈（未优化）
O(log n)	对数空间	二分查找（递归实现）
O(n2)	平方空间	二维数组、动态规划表（未优化）

---

空间复杂度为：O(1)

void example(int n) 
{int a = 0;      // 局部变量，固定空间int b[100];     // 固定大小的数组//常数空间
}

---

空间复杂度为：O(n)

void example(int n) 
{int arr[n];     // 变长数组（VLA），空间随n线性增长// 或int *arr = malloc(n * sizeof(int)); // 动态分配n个intfree(arr);}

---

空间复杂度为：O(log n)

int binarySearch(int arr[], int l, int r, int target) 
{if (l <= r) {int mid = l + (r - l) / 2; // 每次递归只使用常数空间if (arr[mid] == target) return mid;if (arr[mid] < target) return binarySearch(arr, mid + 1, r, target);else return binarySearch(arr, l, mid - 1, target);}return -1;
}

---

空间复杂度为：O(n²)

void example(int n) 
{int matrix[n][n]; // n×n 的二维数组
}

如何优化空间复杂度

• 减少不必要的临时变量
• 直接修改输入数据
• 使用循环代替递归

---

三. 总结

时间复杂度和空间复杂度是评估算法性能的核心指标。时间复杂度衡量算法执行所需操作次数随输入规模 n 的增长趋势，反映执行效率，分析时聚焦最坏情况，忽略常数和低阶项。

空间复杂度则关注算法运行中额外占用的存储空间（如临时变量、递归栈、动态内存），反映内存消耗。

两者常需权衡：例如递归可能降低时间复杂度但增加空间开销，动态规划可能用空间换时间。优化时需结合实际场景，掌握复杂度分析能帮助开发者快速筛选高效算法，避免低效设计，是编程与算法设计的基础能力。

---

往期回顾

C语言—文件操作
C语言—动态内存管理

---

本篇文章到这里就结束了，通过示例代码介绍了时间空间复杂度，如何降低时间空间复杂度的常见问题。文章是博主自己总结后写的，如果哪里有不对的地方，大家可以尽管指出来，博主也会积极改正。最后也感谢大家的评论，点赞，收藏和关注。