线段树学习笔记 - 练习题（1）

1. 前言

线段树系列文章：线段树学习笔记。前一篇学习了线段树，这篇文章就来看下一些线段树题目，还是一样，学习视频：算法讲解111【扩展】线段树专题2-线段树的离散化、二分搜索、特别修改，题目都是左神视频上的，思路也可以看这个视频。

2. LeetCode 699. 掉落的方块

题目链接：699. 掉落的方块。

在二维平面上的 x 轴上，放置着一些方块。

给你一个二维整数数组 positions ，其中 positions[i] = [lefti, sideLengthi] 表示：第 i 个方块边长为 sideLengthi ，其左侧边与 x 轴上坐标点 lefti 对齐。

每个方块都从一个比目前所有的落地方块更高的高度掉落而下。方块沿 y 轴负方向下落，直到着陆到 另一个正方形的顶边 或者是 x 轴上 。一个方块仅仅是擦过另一个方块的左侧边或右侧边不算着陆。一旦着陆，它就会固定在原地，无法移动。

在每个方块掉落后，你必须记录目前所有已经落稳的 方块堆叠的最高高度 。

返回一个整数数组 ans ，其中 ans[i] 表示在第 i 块方块掉落后堆叠的最高高度。

示例 1：

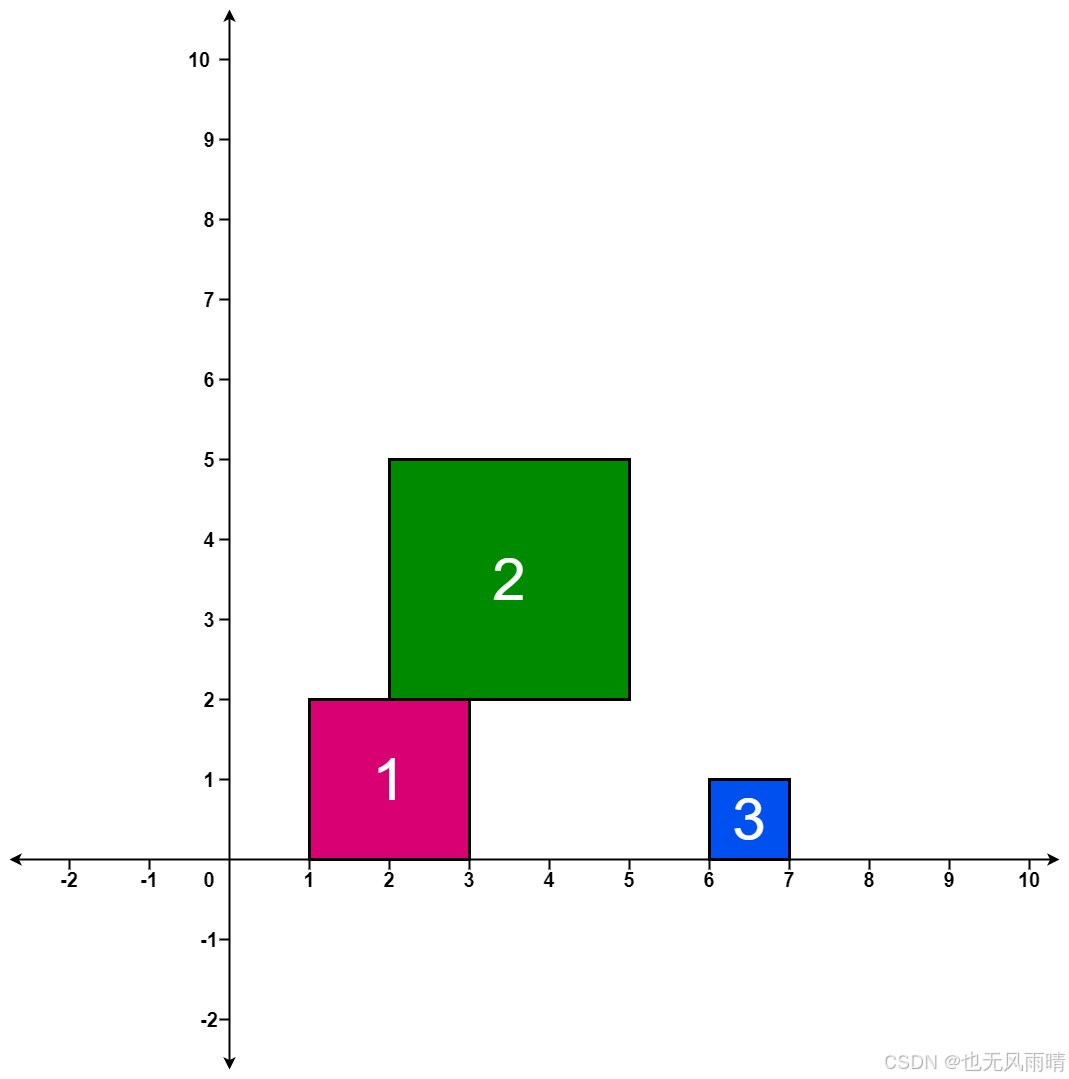
输入：positions = [[1,2],[2,3],[6,1]]
输出：[2,5,5]
解释：

• 第 1 个方块掉落后，最高的堆叠由方块 1 组成，堆叠的最高高度为 2 。
• 第 2 个方块掉落后，最高的堆叠由方块 1 和 2 组成，堆叠的最高高度为 5 。
• 第 3 个方块掉落后，最高的堆叠仍然由方块 1 和 2 组成，堆叠的最高高度为 5 。
  因此，返回 [2, 5, 5] 作为答案。

提示：

• 1 <= positions.length <= 1000
• 1 <= lefti <= $10^8$
• 1 <= sideLengthi <= $10^6$

思路：由于 各个方块是堆在一起的，比如上面图中的 1-3 范围，当处理方块 2 的时候，首先查询出 2-5 的最大值，也就是范围查询最大值，这时候查出来的是 2，然后更新 2-5 的最大值为 2+3 = 5，也就是范围更新，这种涉及到范围查询和范围更新的就直接使用线段树来维护。

数据范围是 $10^8$ 次方，因此如果线段是空间开 $10^8$ 次方，肯定会超出空间限制的，由于 positions 数组的长度是 1000，也就是说假设这 1000 个方块左右端点都不同，因此这种情况下可以使用离散化将每一个点映射成下标，比如上面的 [[1,2],[2,3],[6,1]]，但是在映射之前注意下下面这种情况。

上面两个方块的边界分别是 [1, 2]，[2, 3]，如果我们处理第一个方块的时候把 [1，2] 更新为 1，那么当处理第二个方块的时候查出来 [2，3] 范围最大值就是 1 了，这种情况下假设第二个方块高度为 2，那么 [2，3] 范围就会被更新为 3，这样就有问题了。出现这个问题就是因为没有考虑边界重合，所以我们更新的时候需要重新修改下，更新范围的时候是更新 [l, r - 1]，比如上面 [1，2] 更新的时候会更新 [1，1] 为 1，然后更新 [2，3] 的时候就是更新 [2，2]，这样就不会有问题了，下面看 code。

class Solution {static int MAXN = 10001;static int[] max = new int[MAXN];static int[] update = new int[MAXN];static boolean[] change = new boolean[MAXN];static int[] arr = new int[2001];public void build(int l, int r, int i) {if (l < r) {int mid = l + ((r - l) >> 1);build(l, mid, i << 1);build(mid + 1, r, i << 1 | 1);}max[i] = 0;update[i] = 0;change[i] = false;}public void buildMax(int i) {max[i] = Math.max(max[i << 1], max[i << 1 | 1]);}public void down(int i) {if (change[i]) {lazy(i << 1, update[i]);lazy(i << 1 | 1, update[i]);change[i] = false;}}public void update(int jobl, int jobr, int jobv, int l, int r, int i) {if (jobl <= l && r <= jobr) {lazy(i, jobv);} else {down(i);int mid = l + ((r - l) >> 1);if (jobl <= mid) {update(jobl, jobr, jobv, l, mid, i << 1);}if (jobr > mid) {update(jobl, jobr, jobv, mid + 1, r, i << 1 | 1);}buildMax(i);}}public int query(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return max[i];} else {down(i);int mid = l + ((r - l) >> 1);int max = Integer.MIN_VALUE;if (jobl <= mid) {max = Math.max(max, query(jobl, jobr, l, mid, i << 1));}if (jobr > mid) {max = Math.max(max, query(jobl, jobr, mid + 1, r, i << 1 | 1));}return max;}}public void lazy(int i, int v) {max[i] = v;update[i] = v;change[i] = true;}public List<Integer> fallingSquares(int[][] positions) {List<Integer> res = new ArrayList<>();HashMap<Integer, Integer> map = new HashMap<>();// 离散化int size = 1;for (int[] position : positions) {arr[size++] = position[0];arr[size++] = position[0] + position[1] - 1;}// 用 HashMap 存储数字和下标的映射, O(1) 时间查找Arrays.sort(arr, 1, size);int cnt = 1;for (int i = 1; i < size; i++) {if (!map.containsKey(arr[i])) {map.put(arr[i], cnt++);}}build(1, map.size(), 1);int max = 0;for (int[] position : positions) {// 左int l = map.get(position[0]);// 右边界, 注意要 -1int r = map.get(position[0] + position[1] - 1);// 更新的值为这个范围的最大值加上方块高度int v = query(l, r, 1, map.size(), 1) + position[1];// 求最大值max = Math.max(max, v);res.add(max);update(l, r, v, 1, map.size(), 1);}return res;}
}

3. 洛谷 P4145 上帝造题的七分钟 2 / 花神游历各国

P4145 上帝造题的七分钟 2 / 花神游历各国。

题目背景

XLk 觉得《上帝造题的七分钟》不太过瘾，于是有了第二部。

题目描述

"第一分钟，X 说，要有数列，于是便给定了一个正整数数列。

第二分钟，L 说，要能修改，于是便有了对一段数中每个数都开平方(下取整)的操作。

第三分钟，k 说，要能查询，于是便有了求一段数的和的操作。

第四分钟，彩虹喵说，要是 noip 难度，于是便有了数据范围。

第五分钟，诗人说，要有韵律，于是便有了时间限制和内存限制。

第六分钟，和雪说，要省点事，于是便有了保证运算过程中及最终结果均不超过 $64$ 位有符号整数类型的表示范围的限制。

第七分钟，这道题终于造完了，然而，造题的神牛们再也不想写这道题的程序了。"

——《上帝造题的七分钟·第二部》

所以这个神圣的任务就交给你了。

输入格式

第一行一个整数 $n$，代表数列中数的个数。

第二行 $n$ 个正整数，表示初始状态下数列中的数。

第三行一个整数 $m$，表示有 $m$ 次操作。

接下来 $m$ 行每行三个整数 k l r。

• $k=0$ 表示给 $[l,r]$ 中的每个数开平方（下取整）。

• $k=1$ 表示询问 $[l,r]$ 中各个数的和。

数据中有可能 $l>r$，所以遇到这种情况请交换 $l$ 和 $r$。

输出格式

对于询问操作，每行输出一个回答。

输入输出样例 #1

输入 #1

10
1 2 3 4 5 6 7 8 9 10
5
0 1 10
1 1 10
1 1 5
0 5 8
1 4 8

输出 #1

19
7
6

说明/提示

对于 $30\%$ 的数据，$1\le n,m\le 10^3$，数列中的数不超过 $32767$。

对于 $100\%$ 的数据，$1\le n,m\le 10^5$，$1\le l,r\le n$，数列中的数大于 $0$，且不超过 $10^{12}$。

思路：

首先对于开平方这件事，sum 数组是不能在常数时间内更新完的，因此更新就不能用懒更新，所以我们得评估下如果每一次更新都到最底部的叶子节点上面去更新，那么整体时间复杂度会是多少。

首先我们会维护一个范围最大值，由于每一次范围开平方都会导致这个范围内的所有数字变小，而这些数字只要开方次数够多，最终都会变成 1，因为 1 开平方还是 1，这种情况下我们维护一个范围最大值，如果发现这个范围内的最大值 <= 1，就不再往下发了。

基于上面这点，可以来分析下，由于数据不超过 $10^{12}$，假设这个数组上每一个都是 $10^{12}$，那么最多经过 6 次，这个值就会变成 1。

• $sqrt(10^{12})=10^6$
• $sqrt(10^6)=10^3$
• $sqrt(10^3)=31$
• $sqrt(31)=5$
• $sqrt(5)=2$
• $sqrt(2)=1$

可以看到，最后最多通过 6 次开平方就能变成 1，以后再遇到这个值就不会修改了。由于线段树的树高大概是 ${\log }_{2}n$，而假设每一次范围更新长度都是 n，那么意味着这 n 个数字都需要经过树高来到最底层修改，而每一个数字最多开平方 6 次，因此通过势能分析可以得知最终更新的整体时间复杂度不会超过 $O(6\ast n\ast lo{g}_{2}n)$，所以时间复杂度应该是够用的。

import java.io.*;public class Main {public static int MAXN = 100001;public static long[] arr = new long[MAXN];public static long[] sum = new long[MAXN << 2];// 1.维护最后一层节点的开平方// 2.剪枝public static long[] max = new long[MAXN << 2];public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));StreamTokenizer in = new StreamTokenizer(br);PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));in.nextToken();int n = (int) in.nval;for (int i = 1; i <= n; i++) {in.nextToken();arr[i] = (long) in.nval;}build(1, n, 1);in.nextToken();int m = (int) in.nval;for (int i = 1, op, jobl, jobr, tmp; i <= m; i++) {in.nextToken();op = (int) in.nval;in.nextToken();jobl = (int) in.nval;in.nextToken();jobr = (int) in.nval;if (jobl > jobr) {tmp = jobl;jobl = jobr;jobr = tmp;}if (op == 0) {sqrt(jobl, jobr, 1, n, 1);} else {out.println(query(jobl, jobr, 1, n, 1));}}out.flush();out.close();br.close();}private static long query(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return sum[i];}int mid = l + ((r - l) >> 1);long ans = 0;if (jobl <= mid) {ans += query(jobl, jobr, l, mid, i << 1);}if (jobr > mid) {ans += query(jobl, jobr, mid + 1, r, i << 1 | 1);}return ans;}// 不懒更新了private static void sqrt(int jobl, int jobr, int l, int r, int i) {if (l == r) {// 直接到叶子节点去更新long sqrt = (long) Math.sqrt(max[i]);max[i] = sqrt;sum[i] = sqrt;} else {int mid = l + ((r - l) >> 1);// 不对 1 开平方, 剪枝, 因为着一个数字最多 6 次之后就不会下发了if (jobl <= mid && max[i << 1] > 1) {sqrt(jobl, jobr, l, mid, i << 1);}if (jobr > mid && max[i << 1 | 1] > 1) {sqrt(jobl, jobr, mid + 1, r, i << 1 | 1);}up(i);}}private static void up(int i) {sum[i] = sum[i << 1] + sum[i << 1 | 1];max[i] = Math.max(max[i << 1], max[i << 1 | 1]);}private static void build(int l, int r, int i) {if (l == r) {sum[i] = arr[l];max[i] = arr[l];} else {int mid = l + ((r - l) >> 1);build(l, mid, i << 1);build(mid + 1, r, i << 1 | 1);up(i);}}
}

4. CF438D The Child and Sequence

题目链接：CF438D The Child and Sequence。

题目描述

有一个长度为 $n$ 的数列 {an}\{a_n\}{an​} 和 $m$ 次操作，操作内容如下：

1. 格式为 1 l r，表示求 $\sum _{i=l}^r{a}_i$ 的值并输出。
2. 格式为 2 l r x，表示对区间 $[l,r]$ 内每个数取模，模数为 $x$。
3. 格式为 3 k x，表示将 $a_k$ 修改为 $x$。

$1\le n,m\le 10^5$，$1\le l,r,k\le n$，$1\le x\le 10^9$。

输入格式

第一行两个正整数 $n,m$，分别表示数列长度和操作次数。

第二行给出长为 $n$ 的数列 {an}\{a_n\}{an​}。

接下来 $m$ 行，每行表示一次操作。

输出格式

对于每个操作 $1$，输出答案，每行一个整数。答案可能大于 $2^{31}-1$。

输入输出样例 #1

输入 #1

5 5
1 2 3 4 5
2 3 5 4
3 3 5
1 2 5
2 1 3 3
1 1 3

输出 #1

8
5

输入输出样例 #2

输入 #2

10 10
6 9 6 7 6 1 10 10 9 5
1 3 9
2 7 10 9
2 5 10 8
1 4 7
3 3 7
2 7 9 9
1 2 4
1 6 6
1 5 9
3 1 10

输出 #2

49
15
23
1
9

思路：

可以看到这里也是要维护范围取模以及范围累加和，由于取模这个操作我们不能用 O(1) 的时间完成，所以需要像上面第三节一样分析势能，看看范围取模这个操作整体时间复杂度是多少。

首先我们要看下一个数字如果对 x 取模，最大能变成多少，假设这个数字是 10，那么 10 对 10 以内的数字取模最大会剩下 4，也就是 10%6 = 4，还是一样假设这个数字是 20，那么这个数字对 20 以内的数字取模最大会剩下 9，也就是 20 % 11 = 9，所以我们可以来推测以下就是如果一个数字 n 对这个数字范围内的数字取模，最终最大都不会超过 n/2，也就是每一次取模都会减半，所以需要经过 $lo{g}_{2}n$ 次会减到 1。

所以如果整体时间复杂度可以算到 $O(n\ast lo{g}_{2}n\ast lo{g}_{2}x)$，我们也可以算下，由于 x 范围是 $1\le x\le 10^9$，所以换算下来大概就是 $O(32\ast n\ast lo{g}_{2}n)$，然后关键是这道题里面最后一个操作是单个修改，比如说我们现在有一个数字修改成 1 之后就不需要再访问了，但是如果是范围修改有可能经过 $O(n\ast lo{g}_{2}n\ast lo{g}_{2}x)$ 的时间全部修改成 1 之后又全部一个范围修改都改回 $10^9$，这种情况下时间复杂度就比较高了，但是由于是单点修改，最多每一次修改都只会需要增加 $O(lo{g}_{2}m)$ 这么多的时间复杂度，所以整体往大了估算下就是 $O(n\ast lo{g}_{2}n\ast lo{g}_{2}x+k\ast lo{g}_{2}x)$，k 是 $1\le k\le 10^5$，因此我们可以直接单点修改。

import java.io.*;public class Main {public static int MAXN = 100001;public static long[] arr = new long[MAXN];public static long[] sum = new long[MAXN << 2];public static long[] max = new long[MAXN << 2];public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));StreamTokenizer in = new StreamTokenizer(br);PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));in.nextToken();int n = (int) in.nval;in.nextToken();int m = (int) in.nval;for (int i = 1; i <= n; i++) {in.nextToken();arr[i] = (int) in.nval;}build(1, n, 1);for (int i = 1, op; i <= m; i++) {in.nextToken();op = (int) in.nval;if (op == 1) {in.nextToken();int jobl = (int) in.nval;in.nextToken();int jobr = (int) in.nval;out.println(query(jobl, jobr, 1, n, 1));} else if (op == 2) {in.nextToken();int jobl = (int) in.nval;in.nextToken();int jobr = (int) in.nval;in.nextToken();int jobv = (int) in.nval;mod(jobl, jobr, jobv, 1, n, 1);} else {in.nextToken();int jobi = (int) in.nval;in.nextToken();int jobv = (int) in.nval;update(jobi, jobv, 1, n, 1);}}out.flush();out.close();br.close();}private static void update(int jobi, int jobv, int l, int r, int i) {if (l == r) {sum[i] = max[i] = jobv;} else {int mid = l + ((r - l) >> 1);if (jobi <= mid) {update(jobi, jobv, l, mid, i << 1);} else {update(jobi, jobv, mid + 1, r, i << 1 | 1);}up(i);}}private static void mod(int jobl, int jobr, int jobv, int l, int r, int i) {if (jobv > max[i]) {return;}if (l == r) {sum[i] %= jobv;max[i] %= jobv;} else {int mid = l + ((r - l) >> 1);if (jobl <= mid) {mod(jobl, jobr, jobv, l, mid, i << 1);}if (jobr > mid) {mod(jobl, jobr, jobv, mid + 1, r, i << 1 | 1);}up(i);}}private static long query(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return sum[i];}int mid = l + ((r - l) >> 1);long ans = 0;if (jobl <= mid) {ans += query(jobl, jobr, l, mid, i << 1);}if (jobr > mid) {ans += query(jobl, jobr, mid + 1, r, i << 1 | 1);}return ans;}private static void up(int i) {sum[i] = sum[i << 1] + sum[i << 1 | 1];max[i] = Math.max(max[i << 1], max[i << 1 | 1]);}private static void build(int l, int r, int i) {if (l == r) {sum[i] = arr[l];max[i] = arr[l];} else {int mid = l + ((r - l) >> 1);build(l, mid, i << 1);build(mid + 1, r, i << 1 | 1);up(i);}}}

5. 洛谷 P3740 [HAOI2014] 贴海报

P3740 [HAOI2014] 贴海报。

题目描述

Bytetown 城市要进行市长竞选，所有的选民可以畅所欲言地对竞选市长的候选人发表言论。为了统一管理，城市委员会为选民准备了一个张贴海报的 electoral 墙。

张贴规则如下：

1. electoral 墙是一个长度为 $N$ 个单位的长方形，每个单位记为一个格子；

2. 所有张贴的海报的高度必须与 electoral 墙的高度一致的；

3. 每张海报以 A B 表示，即从第 $A$ 个格子到第 $B$ 个格子张贴海报；

4. 后贴的海报可以覆盖前面已贴的海报或部分海报。

现在请你判断，张贴完所有海报后，在 electoral 墙上还可以看见多少张海报。

输入格式

第一行，两个正整数 $N,M$，分别表示 electoral 墙的长度和海报个数。

接下来 $M$ 行，每行两个正整数 $A_i,B_i$，表示每张海报张贴的位置。

输出格式

输出贴完所有海报后，在 electoral 墙上还可以看见的海报数。

输入输出样例 #1

输入 #1

100 5
1 4
2 6
8 10
3 4
7 10

输出 #1

4

说明/提示

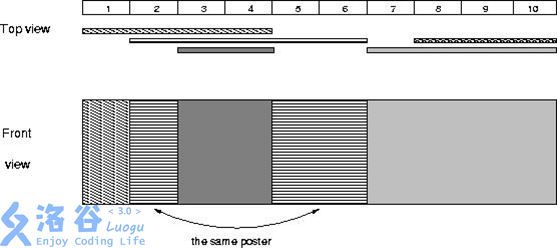
约束条件

$10\le N\le 10000000,1\le M\le 1000,1\le A_i\le B_i\le 10000000$

所有的数据都是正整数，数据之间有一个空格。

思路：

首先由于贴海报这个事就是范围更新，这道题比较特殊就是不需要支持在线范围查询，因此只需要在过程中维护好懒更新的逻辑，最终再汇总一次查询就行，那这样我们直接用一个数组 poster 来表示懒更新的数组，这个数组下标值 poster[i] != 0 就代表这个范围的海报被统一了，如果等于 0 就代表还没有贴海报。

为什么可以用是不是 0 表示呢？上面由于海报的范围是 $1\le A_i\le B_i\le 10000000$，所以如果我们创建出 10000001 长度的数组肯定是超出空间的，所以需要进行离散化，也就是将海报的左右两个点离散成下标值，比如下面图示。

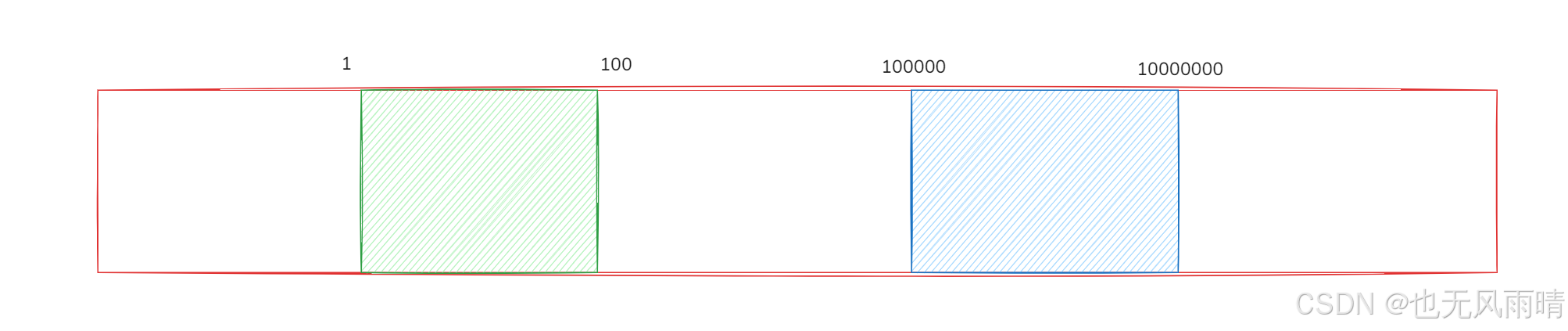
上面有两个海报，左右两个海报 [1，100]，[100000，10000000]，可以把这两个海报的左右端点映射成新的下标值。

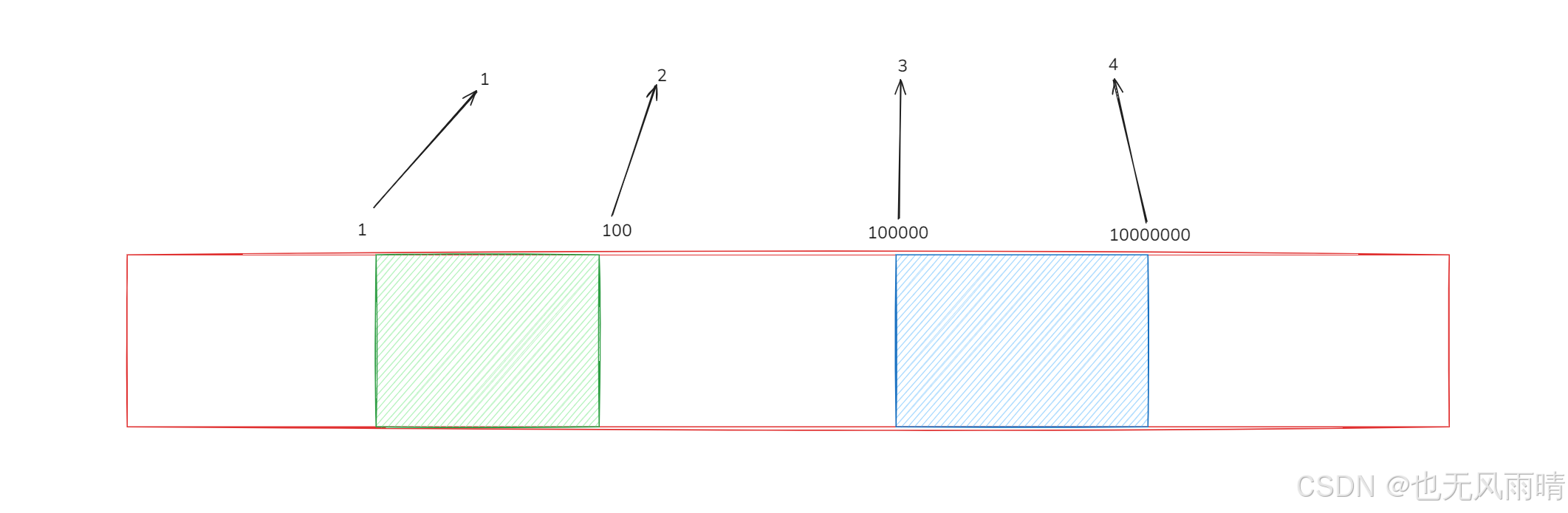
这样我们只需要创建两个长度为 1001 的数 pl 和 pr 来表示海报的左右端点即可，但是有一个问题，比如下面有三张海报。

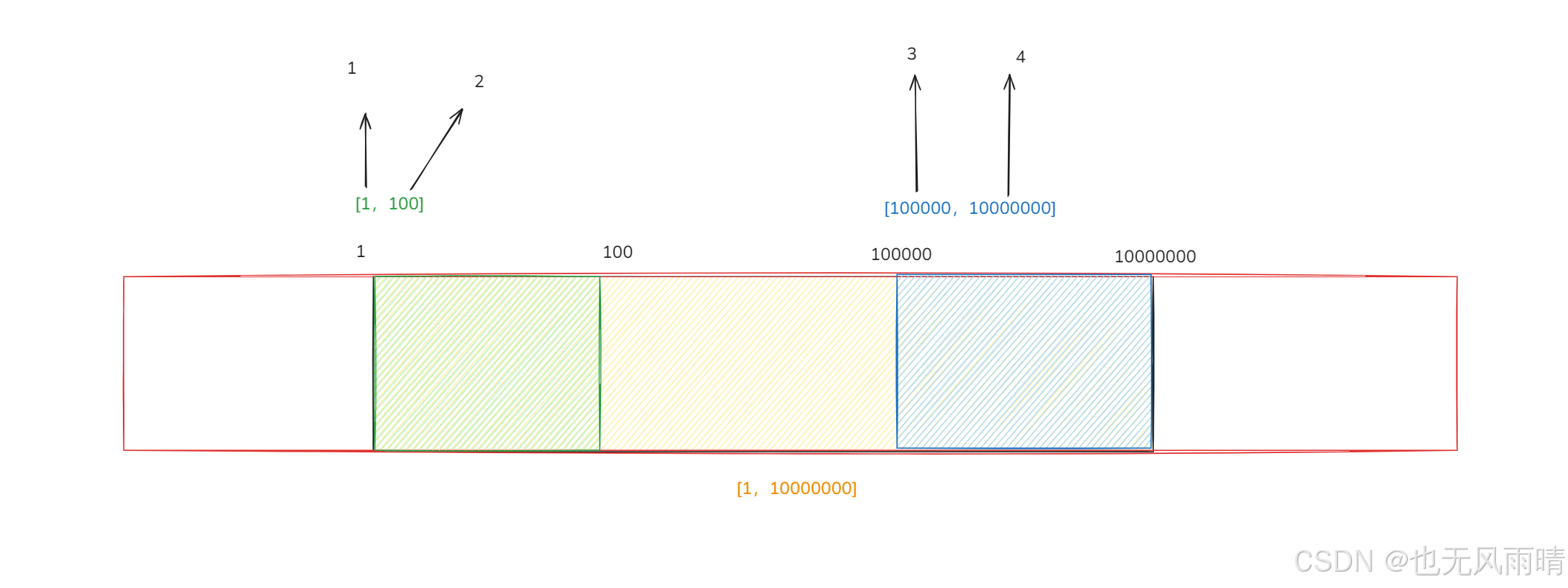
三张海报范围分别是：绿色 [1，100]，蓝色 [100000，10000000]，黄色 [1，1000000]，然后这几个值分别离散化映射为 1、2、3、4，正常来说如果先贴黄色海报，再贴绿色海报和蓝色海报，最终整个范围内是可以看到三张海报的。但是如果离散化之后黄色海报就看不到了。

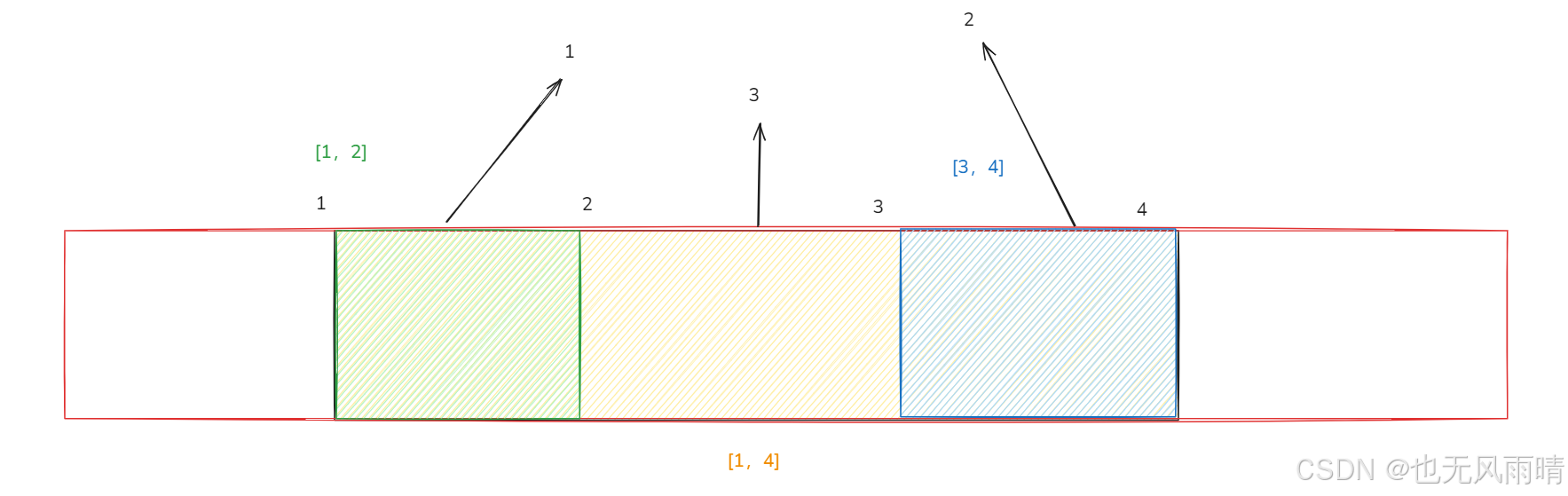
上面离散化之后，绿色 [1，2]，黄色 [1，4]，蓝色 [3，4]，然后先贴黄色海报会把 [1，4] 更新为 3，然后贴绿色海报会把 [1，2] 更新为 1，然后贴蓝色海报会把 [3，4] 更新为 2，这时候再查询 [1，4] 范围上面的海报会发现找不到 3 了。出现这个问题就是因为离散化把一些不该去掉的点都去掉，就像上面的，如果按照原来的范围，那么中间的一个点如 5000 的海报还是 3，但是离散化之后中间点都没有了，于是 3 就丢失了，所以离散化的时候需要判断下，如果两个海报不是贴在一起的，那么需要把中间的一个点也加进去。

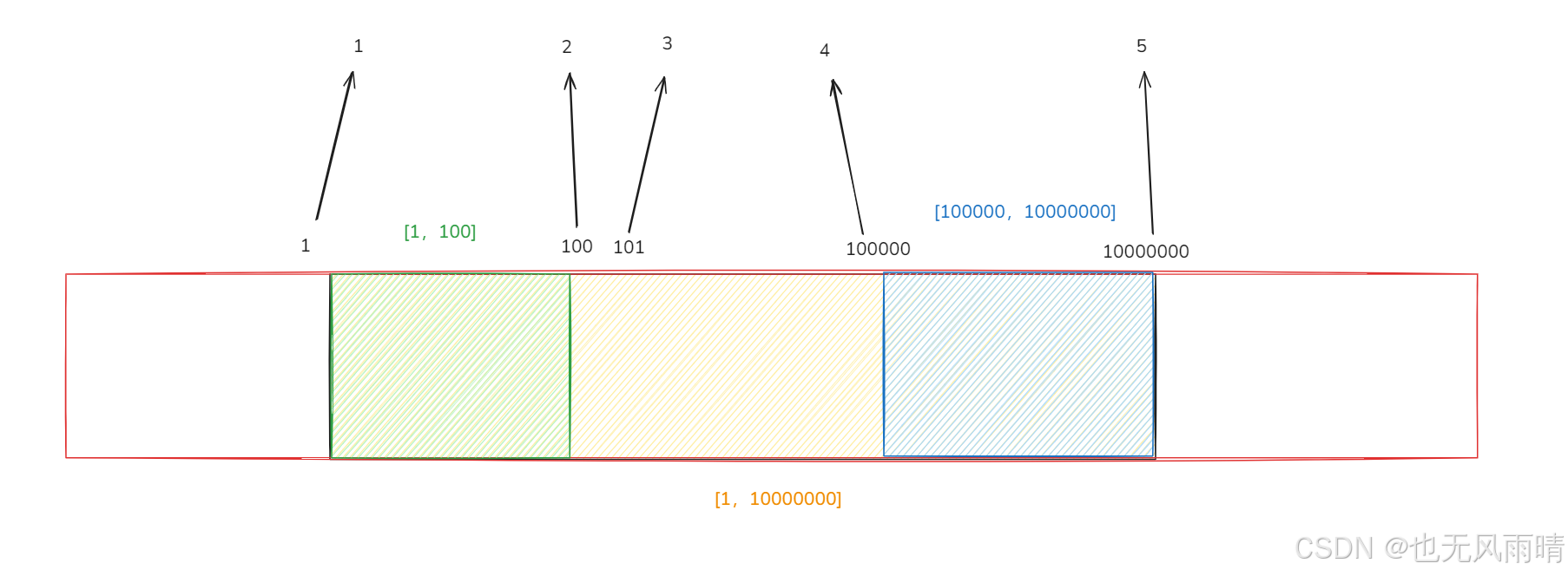
比如 101 这个点就是绿色海报和蓝色海报中间的一个点，把这个点也进行离散化处理，这样最终查询就没问题了，先贴黄色海报会把 [1，5] 更新为 3，然后贴绿色海报会把 [1，2] 更新为 1，然后贴蓝色海报会把 [4，5] 更新为 2，这样最后查询 [1，5] 的颜色就可以查出 3 种了，最终看下 code。

import java.io.*;
import java.util.Arrays;public class Main {public static int MAXN = 1001;// 海报的左右端点public static int[] pl = new int[MAXN];public static int[] pr = new int[MAXN];// 节点public static int[] num = new int[MAXN << 2];public static int[] update = new int[MAXN << 4];public static boolean[] visited = new boolean[MAXN << 2];public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));StreamTokenizer in = new StreamTokenizer(br);PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));in.nextToken();int n = (int) in.nval;int size = 0;// 先把墙的长度加上，离散化别忘了加上墙的长度num[++size] = n;in.nextToken();int m = (int) in.nval;for (int i = 1; i <= m; i++) {in.nextToken();pl[i] = (int) in.nval;in.nextToken();pr[i] = (int) in.nval;num[++size] = pl[i];num[++size] = pr[i];}// 离散化size = discrete(size);build(1, size, 1);// 从 jobl 到 jobr 范围的海报改成 i, 只需要变量标记每一个海报的不同, 因此直接用 i 即可for (int i = 1, jobl, jobr; i <= m; i++) {jobl = search(1, size, pl[i]);jobr = search(1, size, pr[i]);update(jobl, jobr, i, 1, size, 1);}out.println(query(1, search(1, size, n), 1, size, 1));out.flush();out.close();br.close();}private static int query(int jobl, int jobr, int l, int r, int i) {if (l == r) {if (update[i] != 0 && !visited[update[i]]) {visited[update[i]] = true;return 1;}return 0;}down(i);int mid = l + ((r - l) >> 1);int res = 0;if (jobl <= mid) {res += query(jobl, jobr, l, mid, i << 1);}if (jobr > mid) {res += query(jobl, jobr, mid + 1, r, i << 1 | 1);}return res;}public static void down(int i) {if (update[i] != 0) {update[i << 1] = update[i];update[i << 1 | 1] = update[i];update[i] = 0;}}public static void update(int jobl, int jobr, int jobv, int l, int r, int i) {if (jobl <= l && r <= jobr) {update[i] = jobv;} else {down(i);int mid = l + ((r - l) >> 1);if (jobl <= mid) {update(jobl, jobr, jobv, l, mid, i << 1);}if (jobr > mid) {update(jobl, jobr, jobv, mid + 1, r, i << 1 | 1);}}}public static void build(int l, int r, int i) {if (l == r) {update[i] = 0;} else {int mid = l + ((r - l) >> 1);build(l, mid, i << 1);build(mid + 1, r, i << 1 | 1);}}public static int discrete(int size) {// 先排序Arrays.sort(num, 1, size + 1);int p = 1;for (int i = 2; i <= size; i++) {// 离散化if (num[i] != num[p]) {num[++p] = num[i];}}// 如果两个数字差了不止 1int cnt = p;for (int i = 2; i <= p; i++) {if (num[i - 1] + 1 < num[i]) {// 把中间数字也加上num[++cnt] = num[i - 1] + 1;}}// 再次排序Arrays.sort(num, 1, cnt + 1);return cnt;}public static int search(int l, int r, int target) {while (l <= r) {int mid = l + ((r - l) >> 1);if (num[mid] == target) {return mid;} else if (num[mid] > target) {r = mid - 1;} else {l = mid + 1;}}return -1;}}

注意上面离散化 discrete，先排序离散化之后再次判断两个点之间如果相差超过 1，就说明不是贴着的，这时候把中间的一个点也加上，还有一个测试链接：贴海报，数据加强版。

上面洛谷的定义了墙的长度，这里 poj 的墙的长度是无限的，不过代码都是一样的，需要把墙的长度去掉，然后把 MAXN 修改成 10001，最后 query 的时候直接传入 size，洛谷最后 query 还需要找到 size 的下标是因为假设墙的长度是 5000，假设海报范围超过了 5000，那么最后 query 查询的时候也只需要查询 [1，5000] 以内的海报数，那些在墙外的不需要看了。但是这里 poj 的由于没有定义墙的长度，就将离散化之后的最大值 m 传进去来 search。

而 visited 数组是用来防止重复查询的，比如 [2，4] 的海报是 3，那么在遍历到 2 的时候收集了海报，这时候把 visited[3] 设置为 true，下一次遍历到 4 的时候由于 visited[3] = true，就不会重复收集了。

如有错误，欢迎指出！！！