当前位置：首页 > news >正文

河南萌新联赛2025第二场-河南农业大学

news 2025/7/25 20:41:33

一周时间过的这么快，马上第二场的萌新联赛就结束了，对比上一场，这次罚坐的时间更长了，感觉平时学的知识在比赛中根本开不到算法题，这次的A题是一个数论中的整除分块的问题，卡了我好久好久，后来才知道是自己见识短浅了（其实就是一个模板题），卡的我没心态去开其他题了。

打瓦

能想出来这种题目的也是很时髦了，废话不多说，题目来源于：K-打瓦

这是一道签到题，读完题之后就会发现不管输入的是啥，最后都让你输出同一个字符串，那就直接输出即可。

// Problem: 打瓦
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/114408/K
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se secondvoid pre_handle()
{string s;cin>>s;cout<<"gugugaga"<<endl;
} void solve()
{}signed main()
{IOSint T=1;pre_handle();
//	cin>>T;while(T--) solve(); return 0;
}

猜数游戏（esay）

题目链接：I-猜数游戏

这道题很明显最优解就是不断的用二分来取中间值，所以直接用函数log2计算即可，不过要注意如果log之后有剩余的话就还需要加一（向上取整）。因为x是随机的，要想让他采取的次数最多，就要让x等于2（不唯一，相对于1来说2他需要多猜一次）的时候可以让他多猜一次（因为交互机只会告诉他当前猜的数是否大于x，而不会告诉他等于x，当x=2的时候他只知道交互机给出的结果为false，所以他会猜1，结果还是false，那么这时候他才就知道x等于2了）。

// Problem: 猜数游戏(easy)
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/114408/I
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se secondvoid pre_handle()
{} void solve()
{int n;cin>>n;int ans = log2(n);if(pow(2,ans) != n) ans++;cout<<ans<<endl;
}signed main()
{IOSint T=1;pre_handle();
//	cin>>T;while(T--) solve(); return 0;
}

米娅逃离断头台

题目链接：米娅逃离断头台

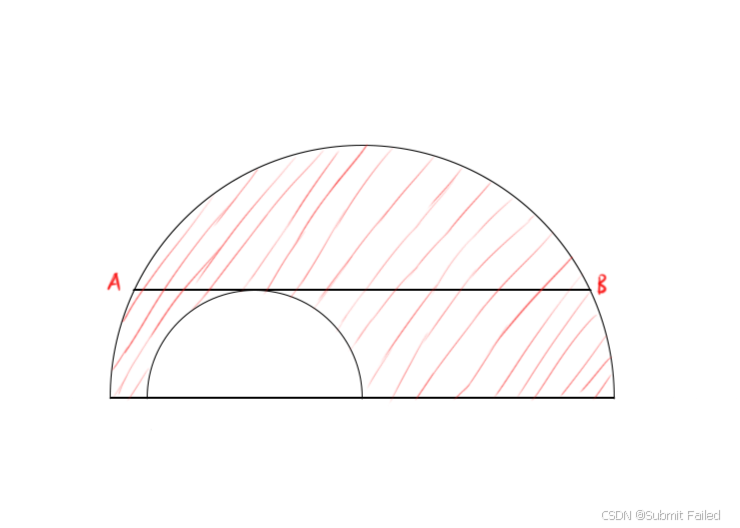
这道题感觉出的挺好的，完全就是数学逻辑，只不过题目中给出的示意图会迷惑你，其实你只要把小半圆移到中间就能发现规律。

要想求阴影部分的面积，就要求出大的半圆的面积减去小的半圆的面积即可，实际上就是只需要知道两个半径就行了，但其实半径具体是多少求不出来，但是可以根据公式来整体替换

ans = 0.5 * π * (R² - r²) 这个就是阴影部分面积的计算公式，那么我们如果将小半圆移到中间再连接OA的时候，就可以发现构成了直角三角形，那么此时就可以根据勾股定理得到如下半径的关系：r² + (x / 2)² = R² 移过来就是 R² - r² = (x / 2)²，而(x / 2)²我们是知道的，因为题目中给出了x的值，所以这道题也就引刃而解了！

// Problem: 米娅逃离断头台
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/114408/M
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
double pi = 3.1415926535;void pre_handle()
{} void solve()
{int x;cin>>x;double r ,R;double xx = x/2.0;//用double精度即可通过 用long doble的话就需要输出llf了xx *= xx;printf("%.2lf\n",0.5 * xx * pi);
}signed main()
{IOSint T=1;pre_handle();
//	cin>>T;while(T--) solve(); return 0;
}

约数个数和

题目链接：约数个数和

这道题要着重讲一下了，因为这道题涉及到了我不会的数论中的整除分块的解法

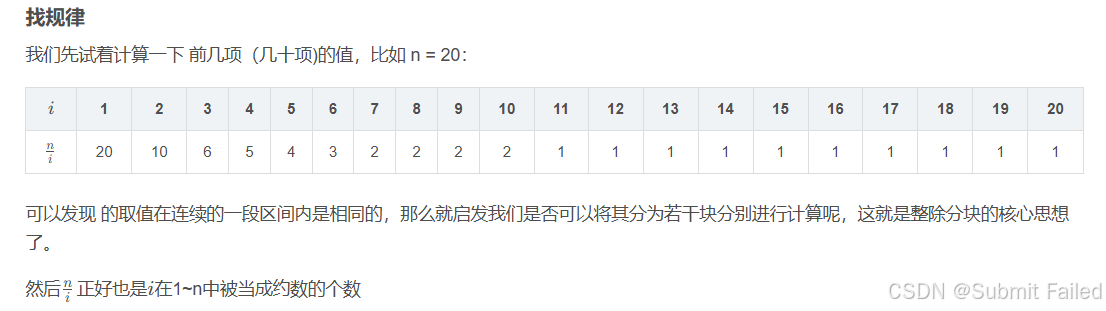整除分块算法（又称数论分块、除法分块）是一种通过分组优化整除计算的技巧，主要用于快速求解包含除法或取整运算的和式。其核心思想是将相同的整除结果分组计算。

在遍历因子的过程中，n/i 代表了从1到n中有多少个i的倍数，然后再通过n/k[n/i]就能算出全为k的区间的右端点，然后由左端点就是上一个右端点+1计算出区间的长度，最后通过求乘积一下子将这个区间内的所有的数都给计算出来，达到跳着遍历的优化实现。详解代码如下：

// Problem: 约数个数和
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/114408/A
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
int n;
void pre_handle()
{//找因子 ——》 找倍数
} void solve()
{cin>>n;int ans=0;int l=1,r=1,k;for(int i=1;i<=n;i++)//枚举所有的因子{k = n/i;//从1到n里面有几个i的倍数r = n/k;//通过整除分块来确定右边界ans += k*(r-l+1);//这个区间内的所有因子在1到n中都有k个该因子的倍数（即他们都作为k个数的因子）l = r+1;//更新完答案之后更新左边界i = r;//直接跳过这段区间 省去大量时间！}cout<<ans<<endl;
}signed main()
{IOSint T=1;pre_handle();
//	cin>>T;while(T--) solve(); return 0;
}

开罗尔网络的备用连接方案

题目链接：开罗尔网络的备用连接方案

这道题就是一个简单的树的应用，用双向无向边将两个点连接起来建树最后遍历将每个点的答案更新即可。

// Problem: 开罗尔网络的备用连接方案
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/114408/D
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define int long long 
#define endl '\n'
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define pii pair<int,int>
#define fi first
#define se second
const int N = 1e5+10;
vector<int> e[N];
vector<int> res(N,0),a(N,0);
int n,q;
void dfs(int x,int w,int f)//因为是无向边 所以用一个参数用来表示这个点的父节点 防止倒着遍历上去了 用以保证正常的树的搜索方式
{int k = a[x]&w;bitset<40> b(k);//位运算之后用bitset来转为二进制 便于统计1的个数res[b.count()]++;//这个点的类型（二进制和点权进行按位与后的1的个数）++for(auto i : e[x])//遍历这个节点的所有子节点（因为是无向边 所以要加一个if防止往上递归）{if(i==f) continue;dfs(i,k,x);//进行正常的数的遍历 i就是子节点 k就是当前的按位与w的状态 x表示在递归这几个子节点的过程中的父节点 因为e[x]中会存他的父节点}
}
void solve()
{cin>>n>>q;for(int i=1;i<=n;i++) cin>>a[i];//每个点的点权for(int i=1;i<n;i++){int u,v;cin>>u>>v;e[u].push_back(v);e[v].push_back(u);}dfs(1,-1,0);//因为要进行与操作所以用-1（二进制全为1）作为dfs的初值while(q--){int x;cin>>x;cout<<res[x]<<endl;}
}signed main()
{IOSint T=1;
//	cin>>T;while(T--) solve(); return 0;
}

沉淀沉淀！！！之后的题目还会在本文更新！

查看全文

http://www.lryc.cn/news/597220.html