一文速通《线性方程组》

目录

一、解题必记知识点

二、解题必备技巧 

三、非齐次线性方程组求解

四、齐次线性方程组求解

★五、解析题目信息，获取暗含条件

---

一、解题必记知识点

(1)

(2)基础解系线性无关，基础解系 = 解空间的一个基，基 = 一组线性无关的、能够生成整个空间的向量。

(3)

(4)

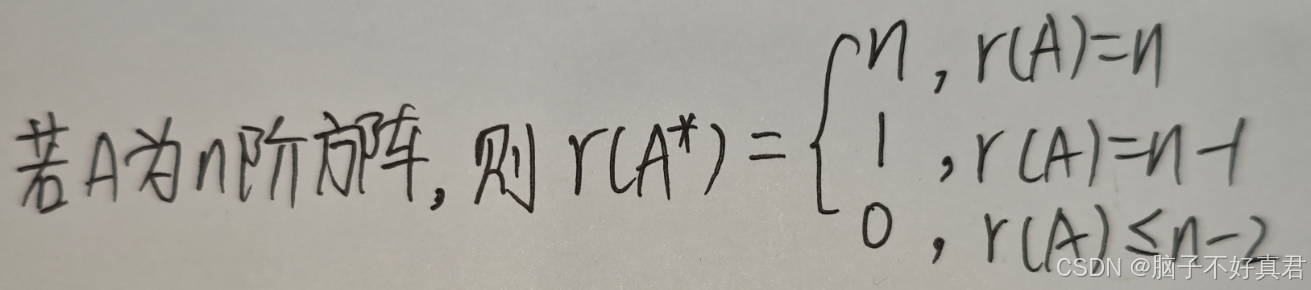
(5)

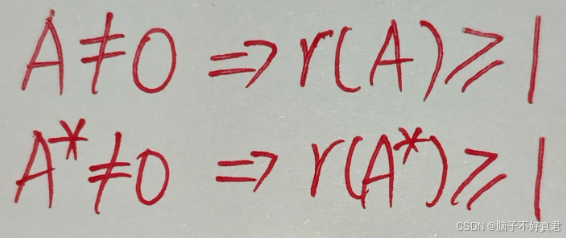
(6)

(7)齐次线性方程组 Ax=0 有非零解的条件是 |A| = 0.

(8)若矩阵B的每个列向量都是方程组 Ax=0 的解 ⟹ AB=0 ⟹ r(A)+r(B)≤n.

二、解题必备技巧 

(1)

(2)

(3) 

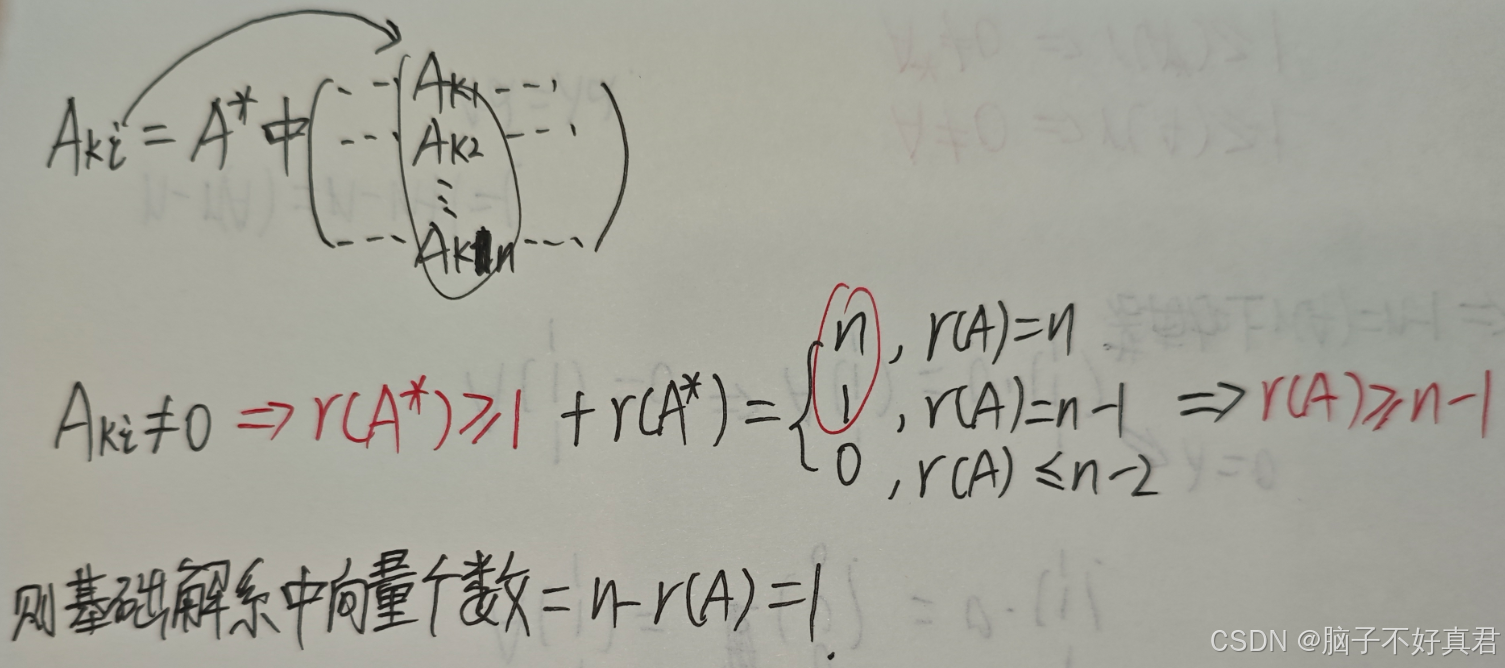
三、非齐次线性方程组求解

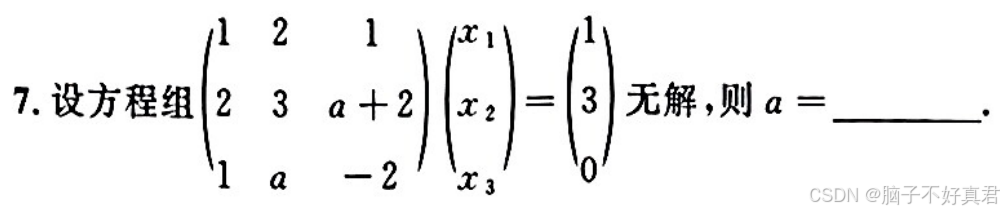
四、齐次线性方程组求解

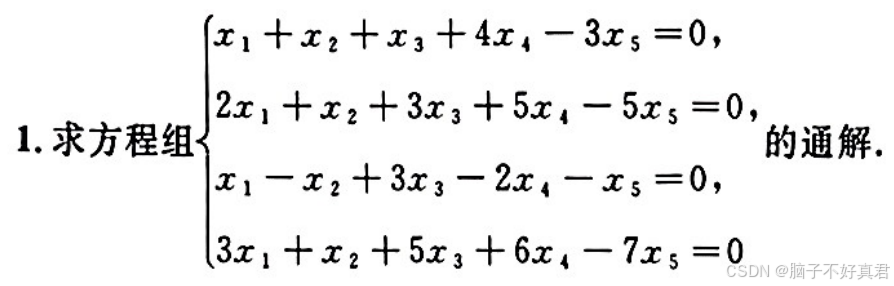
★五、解析题目信息，获取暗含条件

解析题目所给条件，得到题目暗含的信息：

(1) 矩阵的秩，再使用 n-r(A) 就可以得到基础解系中线性无关的向量的个数.

(2) A"▭"=0 ⟹ r(A)+r(▭)≤n.
如下题：

(3) 基础解系中线性无关的向量的个数 ⟹ r(A).

(4) A≠0 ⟹ r(A)≥1.