DFS习题篇【上】

P2089 烤鸡

P2089 烤鸡

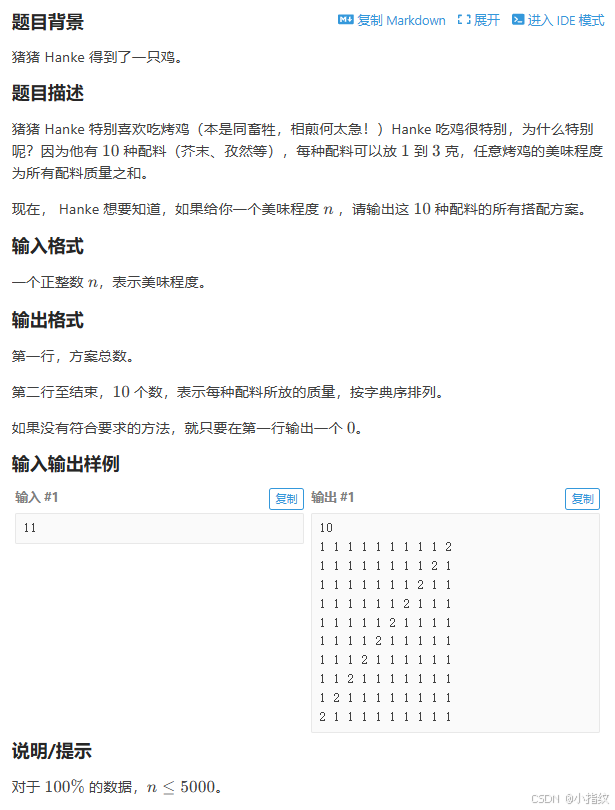
类型：指数型枚举

读题后发现，我们要放十种配料，每种配料可放1~3克，一共的总种类就有10 ~ 30克，我们可以分每个位置讨论，每个位置放1，2，3克（放几克），然后可以将翻案总数求出。。
然后一共是有10种调料，每种调料有三种选择的话，那总的方案数最多有3的10次方种。

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=5005;
int n,a[15],ans=0,m[6000][15];
void dfs(int x,int s)
{if(s>n) return ;//剪枝if(x>10){if(s==n) //当s等于n且满足10种调料时 {ans++;//记录调料的数量 for(int i=1;i<=10;i++)m[ans][i]=a[i];	//将第几种调料存进方便先输出数量再输出每种调料 }return ;}for(int i=1;i<=3;i++){a[x]=i;dfs(x+1,s+i);//传入位置和当前克数 a[x]=0;}
}
void solve()
{cin>>n;dfs(1,0);cout<<ans<<endl;for(int i=1;i<=ans;i++){for(int j=1;j<=10;j++)cout<<m[i][j]<<" ";cout<<endl;} 
}
signed main()
{IOS;int _=1;
//	cin>>_;while(_--)solve();return 0;
}

P1088 火星人

P1088 [NOIP 2004 普及组] 火星人

全排列做法

其实不难看出，比原序列大m其实就是将原序列进行全排列m次，得到的新序列就是。

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=1e4+6;
int n,m,a[N]; 
void solve()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=m;i++)//字典序后的第m就是全排列m次 next_permutation(a+1,a+1+n);for(int i=1;i<=n;i++)cout<<a[i]<<" "; 
}
signed main()
{IOS;int _=1;
//	cin>>_;while(_--)solve();return 0;
}

dfs做法

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=1e4+6;
int n,m,a[N],st[N],ans=0,b[N],f=0; void dfs(int x)
{if(x>n){ans++;if(ans==m+1)//当找到第m {for(int i=1;i<=n;i++){cout<<b[i]<<" ";//输出 }f=1;//输出后就不用往后找了； }return ;}if(!f)//当没有找到时 {for(int i=1;i<=n;i++){if(!ans)i=a[x];if(!st[i]){st[i]=1;b[x]=i;dfs(x+1);b[x]=0;st[i]=0;} }	}}
void solve()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>a[i];dfs(1);  
}
signed main()
{IOS;int _=1;
//	cin>>_;while(_--)solve();return 0;
}

P1149 火柴棒等式

P1149 [NOIP 2008 提高组] 火柴棒等式

需要满足的条件：
A+B=C
A+B+C=n -4
我们用位置选数的方法，一共有三个位置，将每种位置能填的数的情况记录下能满足条件 的情况。

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=1e4+6;
int n,ans;
int a[N];
int s[N]={6,2,5,5,4,5,6,3,7,6};
void dfs(int x,int sum)//位置和当前总和 
{if(sum>n)return ;//剪枝 if(x>3){if(sum==n&&a[1]+a[2]==a[3])//符合条件记录 ans++;return ;}for(int i=0;i<=1000;i++){a[x]=i;dfs(x+1,sum+s[a[x]]);a[x]=0;}
}
void solve()
{cin>>n;n-=4;for(int i=10;i<=1000;i++)//计算出每个数字需要的火柴数 s[i]=s[i%10]+s[i/10]; //通过递归 dfs(1,0);cout<<ans;
}
signed main()
{IOS;int _=1;
//	cin>>_;while(_--)solve();return 0;
}

P2036 PERKET

P2036 [COCI 2008/2009 #2] PERKET

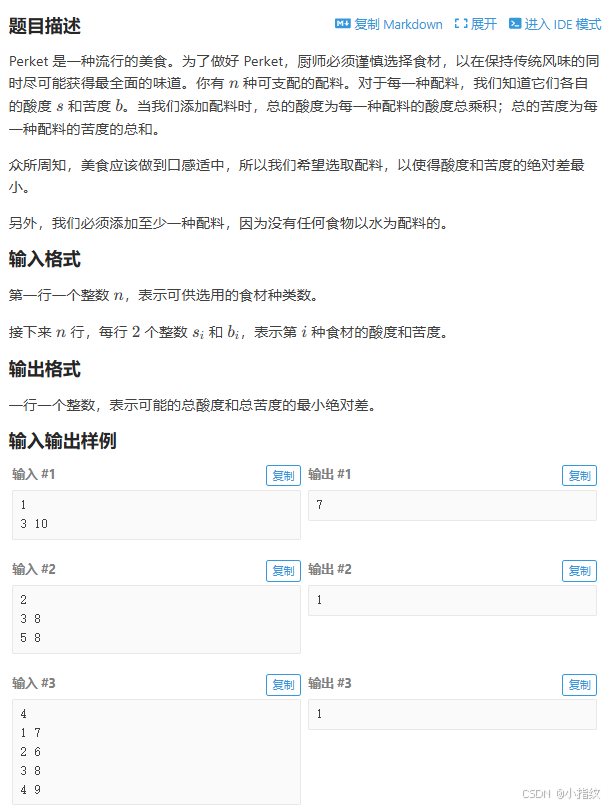
我们可以通过枚举每个位置调料放还是不放，再根据题目计算要求，求出最小的那个。

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=25;
int n;
int a[N];//储存方案
int s[N],k[N];//酸度和苦度
int ans=INT_MAX;//存答案
int st[N];//存每种调料选或不选 
//0表示没考虑到，1选2不选 void dfs(int x)
{if(x>n){bool t1=false;int sum1=1;//存酸度之积int sum2=0;//苦度之和for(int i=1;i<=n;i++){if(st[i]==1){t1=true;sum1*=s[i];sum2+=k[i];	}} if(t1)ans=min(ans,abs(sum1-sum2));return ;}//选st[x]=1;dfs(x+1);st[x]=0; //不选	st[x]=2;dfs(x+1);st[x]=0;
} void solve()
{cin>>n;for(int i=1;i<=n;i++)cin>>s[i]>>k[i];dfs(1);cout<<ans; 
}
signed main()
{IOS;int _=1;
//	cin>>_;while(_--)solve();return 0;
}

P1135 奇怪的电梯

P1135 奇怪的电梯


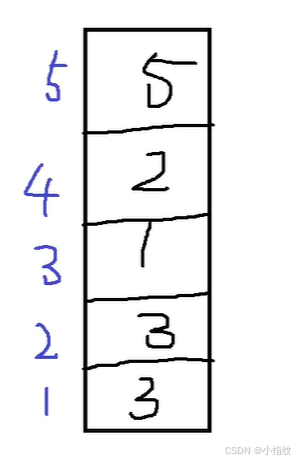
注意这里给出的3是上了三层，而不是上到三楼。
每层楼最多走一次的方案一定比重复走某层楼的方案要更优，因为步数会更少。可以利用全排列的思想枚举

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define int long long
#define PII pair<int,int>
#define fi first
#define se second
#define endl '\n'
const int N=1e4+6;
int n,a,b;
int e[N];
int ans=1e9;
bool st[N];//存每层楼走没走过 
void dfs(int x,int cnt)//当前在x楼，目前按了cnt次按钮 
{if(x<0||x>n)return ;if(cnt>=ans)return ;if(x==b){ans=min(ans,cnt);return ;} 
//	 st[x]=true;//上if(x+e[x]<=n&&!st[x+e[x]]){st[x+e[x]]=true;dfs(x+e[x],cnt+1);st[x+e[x]]=false;}//下if(x-e[x]>0&&!st[x-e[x]]){st[x-e[x]]=true;dfs(x-e[x],cnt+1);st[x-e[x]]=false;}} 
void solve()
{scanf("%lld %lld %lld",&n,&a,&b);for(int i=1;i<=n;i++)scanf("%lld",&e[i]);dfs(a,0);if(ans!=1e9)printf("%lld",ans);elseprintf("-1");
}
signed main()
{IOS;int _=1;
//	cin>>_;while(_--)solve();return 0;
}