当前位置：首页 > news >正文

【每日算法】专题四_前缀和

news 2025/7/22 10:48:58

1. 算法思想

前缀和（Prefix Sum）是一种预处理技术，用于高效解决区间求和、范围查询等问题。其核心思想是通过预先计算数组的累积和，将单次区间查询的时间复杂度从 O (n) 优化到 O (1)。

一维前缀和

核心思想

给定数组 arr = [a₁, a₂, ..., aₙ]，构建前缀和数组 prefix，其中 prefix[i] 表示原数组前 i 个元素的和：

prefix[0] = 0（边界条件，方便处理）
prefix[i] = prefix[i-1] + arr[i-1]（i ≥ 1）

通过前缀和数组，原数组任意区间 [l, r]（闭区间）的和可表示为：

sum(l, r) = prefix[r+1] - prefix[l]

二维前缀和（矩阵区域和）

核心思想

对于二维矩阵 matrix，构建二维前缀和数组 prefix[i][j]，表示从矩阵左上角 (0, 0) 到右下角 (i-1, j-1) 所围成的矩形区域的元素和：

prefix[i][j] = prefix[i-1][j] + prefix[i][j-1] - prefix[i-1][j-1] + matrix[i-1][j-1]

通过二维前缀和数组，任意子矩阵 (x₁, y₁) 到 (x₂, y₂) 的和可表示为：

sum(x₁, y₁, x₂, y₂) = prefix[x₂+1][y₂+1] - prefix[x₁][y₂+1] - prefix[x₂+1][y₁] + prefix[x₁][y₁]

前缀和的应用场景

快速区间求和：如多次查询数组任意子区间的和。
子数组和问题：例如，统计和为 K 的子数组个数（结合哈希表优化）。
滑动窗口变种：优化固定长度窗口的和查询。
二维区域查询：如多次查询矩阵中任意子矩阵的和。

总结

前缀和是一种简单而强大的预处理技术，通过牺牲 O (n) 或 O (n*m) 的空间复杂度，将区间查询的时间复杂度优化到 O (1)。适用于需要频繁查询区间和的场景，尤其在处理静态数据（数据不动态更新）时效果显著。

2. 例题

2.1 一维前缀和

【模板】前缀和_牛客题霸_牛客网

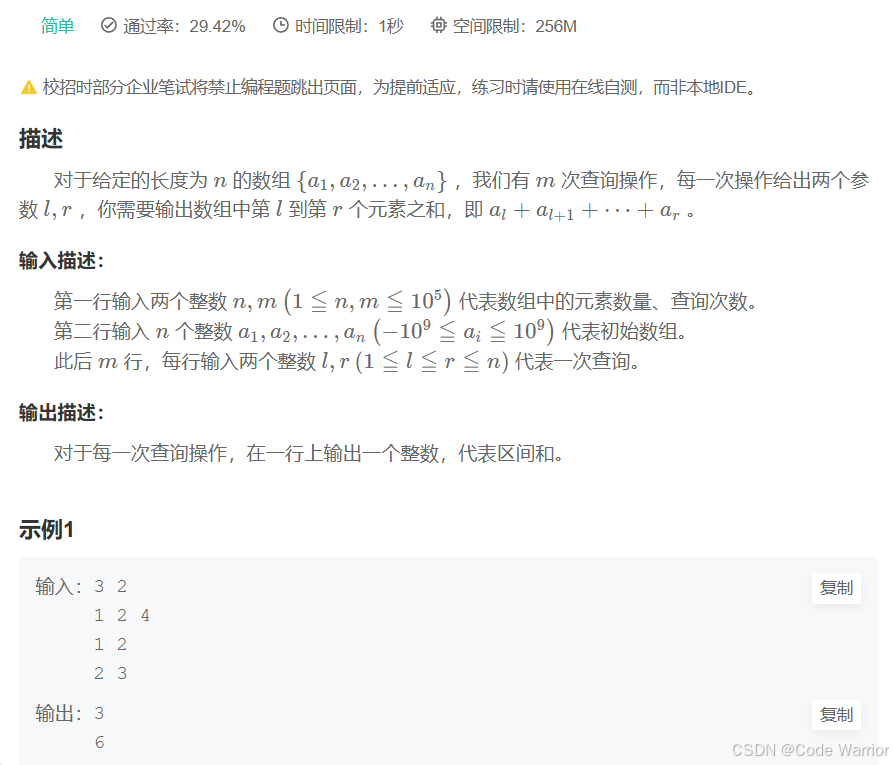
核心思想是利用前缀和数组快速计算区间和，将每次查询的时间复杂度优化为 O (1)。

核心思路

输入处理：读取数组长度 n 和查询次数 m。
前缀和数组构建：
- 遍历数组，计算从首元素到当前位置的累积和，存储在 dp 数组中。
- dp[i] 表示原数组前 i 个元素的和（下标从 1 开始）。
区间查询：
- 对于每个查询 [l, r]，直接通过 dp[r] - dp[l-1] 计算区间和。
- 利用前缀和数组的特性，将单次查询的时间复杂度从 O (n) 降至 O (1)。

int main() {int n = 0, m = 0;cin >> n >> m;vector<long long> arr(n + 1, 0);// 前缀和数组vector<long long> dp(n + 1, 0);for(int i = 1; i < n + 1; ++i){cin >> arr[i];dp[i] = arr[i] + dp[i - 1];}for(int i = 0; i < m; ++i){int l = 0, r = 0;cin >> l >> r;printf("%lld\n", dp[r] - dp[l - 1]);}
}

2.2 二维前缀和

【模板】二维前缀和_牛客题霸_牛客网

核心思想是利用一维前缀和数组快速计算二维矩阵中任意子矩阵的和，将每次查询的时间复杂度优化为 O (n)（n 为子矩阵的行数）。

核心思路

输入处理：读取矩阵的行数 n、列数 m 和查询次数 q。
前缀和数组构建：
- 按行计算前缀和：dp[i][j] 表示矩阵第 i 行前 j 个元素的和。
- 递推公式：dp[i][j] = arr[i][j] + dp[i][j-1]。
子矩阵查询：
- 对于每个查询 (x1, y1, x2, y2)，遍历行区间 [x1, x2]。
- 每行的区间和通过 dp[j][y2] - dp[j][y1-1] 快速计算，累加所有行的和得到子矩阵总和。

关键点

按行预处理：通过预处理每行的前缀和，将二维问题转化为多次一维区间查询。
时间优化：单次查询需遍历子矩阵的所有行，时间复杂度为 O (x2-x1+1)，适用于行数较少的场景。
空间开销：O (n*m) 的额外空间存储前缀和数组。

#include <iostream>
#include <vector>
using namespace std;int main() {int n = 0, m = 0, q = 0;cin >> n >> m >> q;vector<vector<int>> arr(n + 1, vector<int>(m + 1, 0));vector<vector<long long>> dp(n + 1, vector<long long>(m + 1, 0));for(int i = 1; i <= n; ++i){for(int j = 1; j <= m; ++j){cin >> arr[i][j];dp[i][j] = arr[i][j] + dp[i][j - 1];}}for(int i = 0; i < q; ++i){int x1, y1, x2, y2;cin >> x1 >> y1 >> x2 >> y2;long long sum = 0;for(int j = x1; j <= x2; ++j){sum += dp[j][y2] - dp[j][y1 - 1];}cout << sum << endl;}}
// 64 位输出请用 printf("%lld")

2.3 寻找数组的中心下标

724. 寻找数组的中心下标 - 力扣（LeetCode）

核心思想是利用前缀和数组快速找到数组的中心索引，即该索引左侧所有元素的和等于右侧所有元素的和。

核心思路

前缀和数组构建：
- 创建长度为 n+2 的前缀和数组 dp，其中 dp[i+1] 表示原数组前 i 个元素的和（nums[0] 到 nums[i-1]）。
- 递推公式：dp[i+1] = dp[i] + nums[i]。
中心索引判断：
- 遍历每个可能的中心索引 i（对应原数组下标 i-1）。
- 左侧和为 dp[i-1]，右侧和为 dp[n] - dp[i]（即总和减去左侧和与当前元素）。
- 若两侧和相等，则返回当前索引 i-1。
边界处理：
- 当 i=1 时，左侧和为 0（对应原数组下标 0 左侧无元素）。
- 当 i=n 时，右侧和为 0（对应原数组下标 n-1 右侧无元素）。

关键点

前缀和优化：通过预处理前缀和数组，将每次判断的时间复杂度从 O (n) 降至 O (1)。
索引转换：前缀和数组 dp 的索引比原数组 nums 多 1，需注意转换关系（如 dp[i+1] 对应 nums[i]）。
空间开销：O (n) 的额外空间存储前缀和数组。

class Solution {
public:int pivotIndex(vector<int>& nums) {int n = nums.size();// 前缀和数组vector<int> dp(n + 2, 0);for(int i = 0; i < n; ++i)dp[i + 1] = dp[i] + nums[i];for(int i = 1; i <= n; ++i){if(dp[i - 1] == dp[n] - dp[i]){return i - 1;}}return -1;}
};

2.4 除自身以外数组的乘积

238. 除自身以外数组的乘积 - 力扣（LeetCode）

核心思想是利用前缀乘积和后缀乘积数组，在不使用除法的情况下，线性时间内计算每个元素除自身外的乘积。

核心思路

前缀乘积数组 prefix：
- prefix[i+1] 存储原数组前 i 个元素的乘积（即 nums[0] 到 nums[i-1] 的累积乘积）。
- 初始化 prefix[0] = 1，递推公式：prefix[i+1] = prefix[i] * nums[i]。
后缀乘积数组 suffix：
- suffix[i] 存储原数组从第 i 个元素到末尾的乘积（即 nums[i] 到 nums[n-1] 的累积乘积）。
- 初始化 suffix[n] = 1，递推公式：suffix[i] = suffix[i+1] * nums[i]。
结果数组计算：
- 对于每个位置 i，其结果为 prefix[i] * suffix[i+1]，即：
  - 左侧所有元素的乘积（不包含 nums[i]） × 右侧所有元素的乘积（不包含 nums[i]）。

关键点

空间换时间：通过预处理前缀和后缀乘积数组，将单次查询的时间复杂度从 O (n) 优化到 O (1)。
索引对应：prefix 和 suffix 的索引需与原数组 nums 正确对应，避免越界。
边界处理：
- prefix[0] = 1：表示左侧无元素时的乘积为 1。
- suffix[n] = 1：表示右侧无元素时的乘积为 1。

复杂度分析

时间复杂度：O (n)，三次线性遍历。
空间复杂度：O (n)，存储前缀和后缀数组。

class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> prefix(n + 1, 1);vector<int> suffix(n + 1, 1);vector<int> ans(n);// 计算前缀乘积for (int i = 0; i < n; ++i) {prefix[i + 1] = prefix[i] * nums[i];}// 计算后缀乘积for (int i = n - 1; i >= 0; --i) {suffix[i] = suffix[i + 1] * nums[i];}// 计算结果for (int i = 0; i < n; ++i) {ans[i] = prefix[i] * suffix[i + 1];}return ans;}
};

2.5 和为 K 的子数组

560. 和为 K 的子数组 - 力扣（LeetCode）

核心思想是利用哈希表优化前缀和查询，在线性时间内统计数组中和为 k 的连续子数组个数。

核心思路

前缀和转化问题：
- 对于数组 nums，若存在子数组 [j+1, i] 的和为 k，则其前缀和满足：
  prefix[i] - prefix[j] = k ⇒ prefix[j] = prefix[i] - k。
- 因此，问题转化为：遍历到位置 i 时，统计之前有多少个前缀和等于 prefix[i] - k。
哈希表加速查询：
- 使用哈希表 hash 记录每个前缀和出现的次数。
- 遍历数组时，累加当前元素到 sum，检查 sum - k 是否存在于哈希表中，若存在则将对应次数累加到结果 count 中。
- 更新哈希表，记录当前前缀和 sum 的出现次数。
初始条件处理：
- 初始化 hash[0] = 1，处理子数组从下标 0 开始的情况（即 prefix[i] = k 的情况）。

关键点

哈希表的作用：快速统计历史前缀和中等于 sum - k 的次数，将时间复杂度从 O (n²) 优化到 O (n)。
前缀和差值的意义：若 sum - k 曾出现过，则说明从该位置到当前位置的子数组和为 k。
边界处理：hash[0] = 1 确保当 sum 恰好等于 k 时能正确统计。

复杂度分析

时间复杂度：O (n)，单次遍历数组。
空间复杂度：O (n)，哈希表存储前缀和及其次数。

class Solution {
public:int subarraySum(vector<int>& nums, int k) {// 要想求该数组中和为 k 的子数组的个数，可转化为求i遍历// 该数组时，在区间[0, i - 1]中前缀和为nums[i] - k的个数的总和unordered_map<int,int> hash;hash[0] = 1;//当nums[i] - k等于0的情况int count = 0, sum = 0;for(auto x : nums){sum += x;if(hash.count(sum - k))count += hash[sum - k];++hash[sum];}return count;}
};

2.6 和可被 K 整除的子数组

974. 和可被 K 整除的子数组 - 力扣（LeetCode）

核心思想是利用同余定理和哈希表，在线性时间内统计数组中和能被 k 整除的连续子数组个数。

核心思路

同余定理应用：
- 若子数组 [j+1, i] 的和能被 k 整除，则其前缀和满足：
  (prefix[i] - prefix[j]) % k == 0 ⇒ prefix[i] ≡ prefix[j] (mod k)。
- 因此，问题转化为：遍历到位置 i 时，统计之前有多少个前缀和与 prefix[i] 模 k 同余。
哈希表记录余数频次：
- 使用哈希表 hash 记录每个余数 r = prefix[i] % k 出现的次数。
- 遍历数组时，累加当前元素到 sum，计算 sum % k（处理负数取模），检查该余数是否存在于哈希表中，若存在则将对应次数累加到结果 count 中。
- 更新哈希表，记录当前余数的出现次数。
初始条件处理：
- 初始化 hash[0] = 1，处理前缀和本身就能被 k 整除的情况（即子数组从下标 0 开始）。

关键点

负数取模处理：
由于 C++ 中负数取模结果可能为负（如 -5 % 3 = -2），需通过 (sum % k + k) % k 确保余数为正（如 -2 + 3 = 1）。
同余定理的优化：
若两个前缀和模 k 同余，则它们的差必为 k 的倍数，因此可用哈希表快速统计符合条件的子数组个数。

复杂度分析

时间复杂度：O (n)，单次遍历数组。
空间复杂度：O (k)，哈希表最多存储 k 种不同的余数。

class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {// 同余定理，即(a - b) % k = 0 -> a % k = b % kunordered_map<int, int> hash;// 哈希表存的是前缀和模k后的值++hash[0 % k];// sum当好等能被k整除的情况int sum = 0, count = 0;for(auto x : nums){sum += x;// 当前位置的前缀和int r = (sum % k + k) % k;if(hash.count(r)) count += hash[r];++hash[r];}return count;}
};

2.7 连续数组

525. 连续数组 - 力扣（LeetCode）

核心思想是通过将 0 转换为 - 1，利用前缀和与哈希表在线性时间内找到最长的连续子数组，使其 0 和 1 的数量相等。

核心思路

数值转换：
- 将数组中的所有 0 替换为 -1，使得子数组和为 0 等价于该子数组中 0 和 1 的数量相等。
前缀和与哈希表：
- 使用哈希表 hash 记录每个前缀和首次出现的下标。
- 遍历数组时，累加当前元素到 sum：
  - 若 sum 已在哈希表中，说明从首次出现位置到当前位置的子数组和为 0，更新最大长度。
  - 否则，记录 sum 的首次出现位置。
初始条件处理：
- 初始化 hash[0] = -1，处理前缀和本身为 0 的情况（即子数组从下标 0 开始）。

关键点

0→-1 转换的意义：
将问题转化为 “和为 0 的最长子数组”，利用前缀和的性质快速求解。
哈希表的作用：
记录前缀和的首次出现位置，确保每次找到的子数组是最长的。若当前 sum 已存在，说明中间段的和为 0。

复杂度分析

时间复杂度：O (n)，单次遍历数组。
空间复杂度：O (n)，哈希表最多存储 n 个不同的前缀和。

class Solution {
public:int findMaxLength(vector<int>& nums) {// 将所有的零变成-1这样的话数组内元素相加等于0就说明数组内具有相同数量的0和1int n = nums.size();for(int i = 0; i < n; ++i)if(nums[i] == 0) nums[i] = -1;// <前缀和, 下标>unordered_map<int, int> hash;hash[0] = -1; //sum等于0的情况// x = sum;int len = 0, sum = 0;for(int i = 0; i < n; ++i){sum += nums[i];if(hash.count(sum)) len = max(len, i - hash[sum]);else hash[sum] = i;}return len;}
};

2.8 矩阵区域和

1314. 矩阵区域和 - 力扣（LeetCode）

核心思想是利用二维前缀和快速计算矩阵中每个元素周围指定范围内的子矩阵和，将每次查询的时间复杂度优化为 O (1)。

核心思路

二维前缀和预处理
- 构建前缀和数组 dp，其中 dp[i][j] 表示原矩阵左上角 (0,0) 到 (i-1,j-1) 围成的矩形区域的元素和。
- 递推公式：dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + mat[i-1][j-1]（容斥原理，避免重复计算）。
子矩阵范围确定
- 对于每个元素 (i,j)，其周围 k 范围内的子矩阵边界为：
  - 左上角 (x1,y1)：x1 = max(0, i-k)，y1 = max(0, j-k)（防止越界）。
  - 右下角 (x2,y2)：x2 = min(m-1, i+k)，y2 = min(n-1, j+k)（防止越界）。
子矩阵和计算
- 利用前缀和公式计算上述子矩阵的和：
  ret[i][j] = dp[x2+1][y2+1] + dp[x1][y1] - dp[x1][y2+1] - dp[x2+1][y1]。

关键点

二维前缀和的作用：通过预处理将任意子矩阵和的计算从 O (mn) 降至 O (1)，大幅提升效率。
边界处理：使用 max 和 min 确保子矩阵范围不超出原矩阵边界。
索引转换：前缀和数组 dp 比原矩阵多一行一列（从 1 开始），需注意坐标对应关系。

class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m = mat.size(), n = mat[0].size();// 二维数组前缀和vector<vector<int>> dp(m + 1, vector<int>(n + 1));for(int i = 1; i <= m; ++i){for(int j = 1; j <= n; ++j)dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];}vector<vector<int>> ret(m, vector<int>(n));for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){int x1 = max(0, i - k) + 1, y1 = max(0, j - k) + 1;int x2 = min(m - 1, i + k) + 1, y2 = min(n - 1, j + k) + 1;ret[i][j] = dp[x2][y2] + dp[x1 - 1][y1 - 1] - dp[x1 - 1][y2] - dp[x2][y1 - 1];}}return ret;}
};

查看全文

http://www.lryc.cn/news/595223.html