数据结构自学Days10 -- 二叉树的常用实现

✅ 一、为什么要学习二叉树？

1. 📦 组织数据的高效方式

• 二叉树可以快速插入、删除、查找数据，尤其在平衡时，时间复杂度为 $O(\log n)$。

• 适合表示分层结构（如组织结构、文件系统、语法树）。

2. 💡 各种高级结构的基础

很多更复杂的数据结构都以二叉树为基础，例如：

• 堆（Heap）：用于实现优先队列

• 平衡树（如 AVL、红黑树）：用于快速搜索和动态数据更新

• 线段树、区间树、树状数组：用于范围查询

• 表达式树、Huffman 树：用于编译器、压缩算法等

3. 🧠 算法题中的常客

• 很多算法竞赛、笔试题会考查二叉树的构造、遍历、查找、平衡、路径计算等问题。

• 是程序员面试中的高频知识点

4、二叉树的常用功能

功能	说明
✅ 遍历	先序、中序、后序、层序遍历
🔍 搜索	二叉搜索树（BST）可高效查找
📁 分层结构表示	文件系统、组织架构树、语法树
🧮 表达式处理	表达式树支持中缀转后缀、求值
🧠 平衡维护	AVL、红黑树保证查找平衡性
🔧 范围查询	线段树、区间树等支持快速区间操作
🔗 哈夫曼编码	构造最优前缀编码
🔄 结构转换	镜像、翻转、扁平化等结构操作

二叉树是一种既基础又强大的数据结构，学习它不仅是算法的入门，也是迈向更高阶算法和工程应用的必经之路。

下面我们总结一下对于二叉树言的常用接口包括：

二、二叉树的常用实现

1、如何创建二叉树。2、销毁创建的二叉树释放内存。3、计算二叉树的节点个数。4、计算二叉树叶节点的个数。5、计算二叉树第k层的节点个数。6、找到二叉树中指定的节点。7、二叉树的前序，后序，中序。8、层序遍历（利用队列实现）。9、判断是否为完全二叉树。

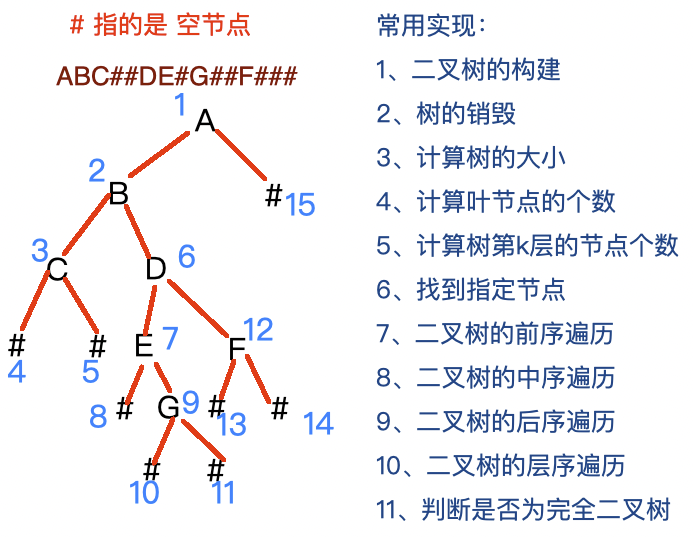
1、如何创建二叉树

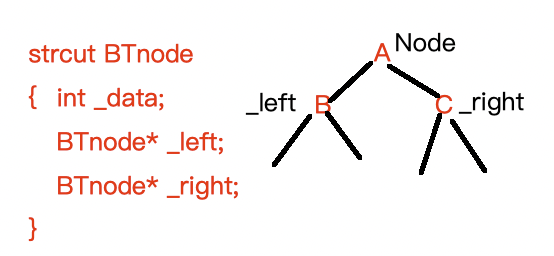
代码实现：

typedef char BTreeDataType;typedef struct BTreeNode
{BTreeDataType _data;struct BTreeNode* _left;struct BTreeNode* _right;
}BTreeNode;BTreeNode* CreateTree(BTreeDataType* str,int* pi){if(*str == '\0'){return NULL;}if(str[*pi] == '#'){(*pi)++;return NULL;}BTreeNode* root = (BTreeNode*)malloc(sizeof(BTreeNode));root->_data = str[*pi];(*pi)++;root->_left = CreateTree(str,pi);root->_right = CreateTree(str,pi);return root;
}

测试函数：

int main(){char str[100] = {0};scanf("%s",str);int i = 0;BTreeNode* root = CreateTree(str,&i);}

输入：ABC##DE#G##F###，注意这里我们构建二叉树是通过“前序遍历的思想”

2、销毁创建的二叉树释放内存

void BTree_Destroy(BTreeNode* root){if(!root){return;}BTree_Destroy(root->_left);BTree_Destroy(root->_right);free(root);root = NULL;
}

3、计算二叉树的节点个数

        利用前序遍历的思想进行二叉树的遍历，统计非空子树即可，可参考二叉树的前序遍历。

int BTreeSize(BTreeNode* root){if(!root){return 0;}return 1+ BTreeSize(root->_left)+BTreeSize(root->_right);
}

4、计算二叉树叶节点的个数

        同样你可以利用前序遍历的思想，但是统计叶节点，需满足左右子树为空才统计

int BTreeLeafSize(BTreeNode* root){if(!root){return 0;}if(!(root->_left) && !(root->_right)){return 1;}return (BTreeLeafSize(root->_left)+BTreeLeafSize(root->_right));
}

5、计算二叉树第k层的节点个数。

        这里我们需要输入k这个参数，首先我们需要找到第k层，当遍历二叉树时，遍历至当前节点的左右子树，则k--，知道k==0时，就是我们的第k层，然后在统计节点个数就行。        

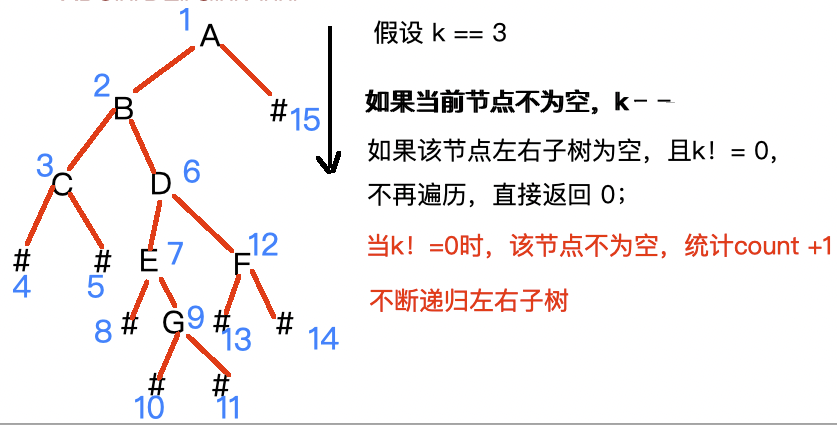
代码实现:

int BTreeLevelKSize(BTreeNode* root,int k){if(!root){return 0;}k--;if(k == 0){return 1;}return (BTreeLevelKSize(root->_left,k)+BTreeLevelKSize(root->_right,k));
}

6、找到二叉树中指定的节点

        只需判断节点值是否为指定值，是就直接返回当前节点，否则继续遍历。

代码实现：

BTreeNode* BTreeFind(BTreeNode* root,int _val){if(!root){return NULL;}if(root->_data == _val){return root;}BTreeNode* node = BTreeFind(root->_left,_val);if(node){return node;}node = BTreeFind(root->_right,_val);if(node){return node;}return NULL;
}

7、二叉树的前序，后序，中序

        这部分内容我们已经实现过很多次了，这里直接给出源码

代码实现：

//前序
void PreOrder(BTreeNode* root){if(!root){printf("NULL");return;}printf("%c ",root->_data);PreOrder(root->_left);PreOrder(root->_right);return;
}
//中序
void InOrder(BTreeNode* root){if(!root){printf("NULL");return;}InOrder(root->_left);printf("%c ",root->_data);InOrder(root->_right);return;
}
//后序
void PostOrder(BTreeNode* root){if(!root){printf("NULL");return;}PostOrder(root->_left);PostOrder(root->_right);printf("%c ",root->_data);return;
}

8、层序遍历（利用队列实现）

        这里我们需要使用到队列的思想，“先进先出”，当前节点不为空，我们把当前节点放入队列中，然后再输出该节点，然后将该节点的左右子节点放入队列，然后再删除左节点，再把左节点的左右子节点再放入，当节点为空时不再放入，当队列为空时不在放出，不断重复放入放出。就是层序遍历。

思维导图：

代码实现：

//队列的声明
typedef struct Queue
{QueueDataType btnode;struct Queue* next;}Queue;typedef struct my_Queue{Queue* _head;Queue* _tail;
}my_Queue;//队列初始化
my_Queue* Queue_Init(){my_Queue* pq = (my_Queue*)malloc(sizeof(my_Queue));pq->_head = pq->_tail = NULL;return pq;
}
//队列的摧毁
void QueueDestroy(my_Queue* pq){assert(pq);Queue* Cur = pq->_head;while (Cur){Queue* Del = Cur;Cur = Cur->next;free(Del);}pq->_head = pq->_tail = NULL;return;
}
//插入元素
void QueuePush(my_Queue* pq,QueueDataType _val){assert(pq);Queue* NewNode = (Queue*)malloc(sizeof(Queue));NewNode->btnode = _val;NewNode->next = NULL;if(pq->_head == NULL){pq->_tail = NewNode;pq->_head = NewNode;  }else{pq->_tail->next = NewNode;pq->_tail = NewNode;}
}
// 删除元素
void QueuePop(my_Queue* pq){assert(pq);if(pq->_head == NULL){return;}else{Queue* Cur = pq->_head;pq->_head = (pq->_head)->next;free(Cur);}if(pq->_head == NULL){pq->_tail = NULL;}return;
}// 返回队列开头元素
QueueDataType QueueFront(my_Queue* pq){assert(pq);if(pq->_head){return pq->_head->btnode;}return NULL;
}//判断队列是否为空
bool IsQueueEmpty(my_Queue* pq){assert(pq);return !pq->_head;
}

队列的构建以及常用函数的实现：参考栈与队列的实现

//层序遍历
void BTree_LevelOrder(BTreeNode* root){if(!root){printf("NULL");return;}my_Queue* BTqueue = Queue_Init();QueuePush(BTqueue,root);while (!IsQueueEmpty(BTqueue)){QueueDataType Front = QueueFront(BTqueue);printf("%c ",Front->_data);QueuePop(BTqueue);if(Front->_left){QueuePush(BTqueue,Front->_left);};if(Front->_right){QueuePush(BTqueue,Front->_right);}}QueueDestroy(BTqueue);BTqueue = NULL;return;
}

9、判断是否为完全二叉树。

        完全二叉树的概念是 除最后一层外，其他层都是满的，且最后一层从左到右连续填满。

这里我们需要利用层序遍历的思想去判断是否为完全二叉树。

思维导图：

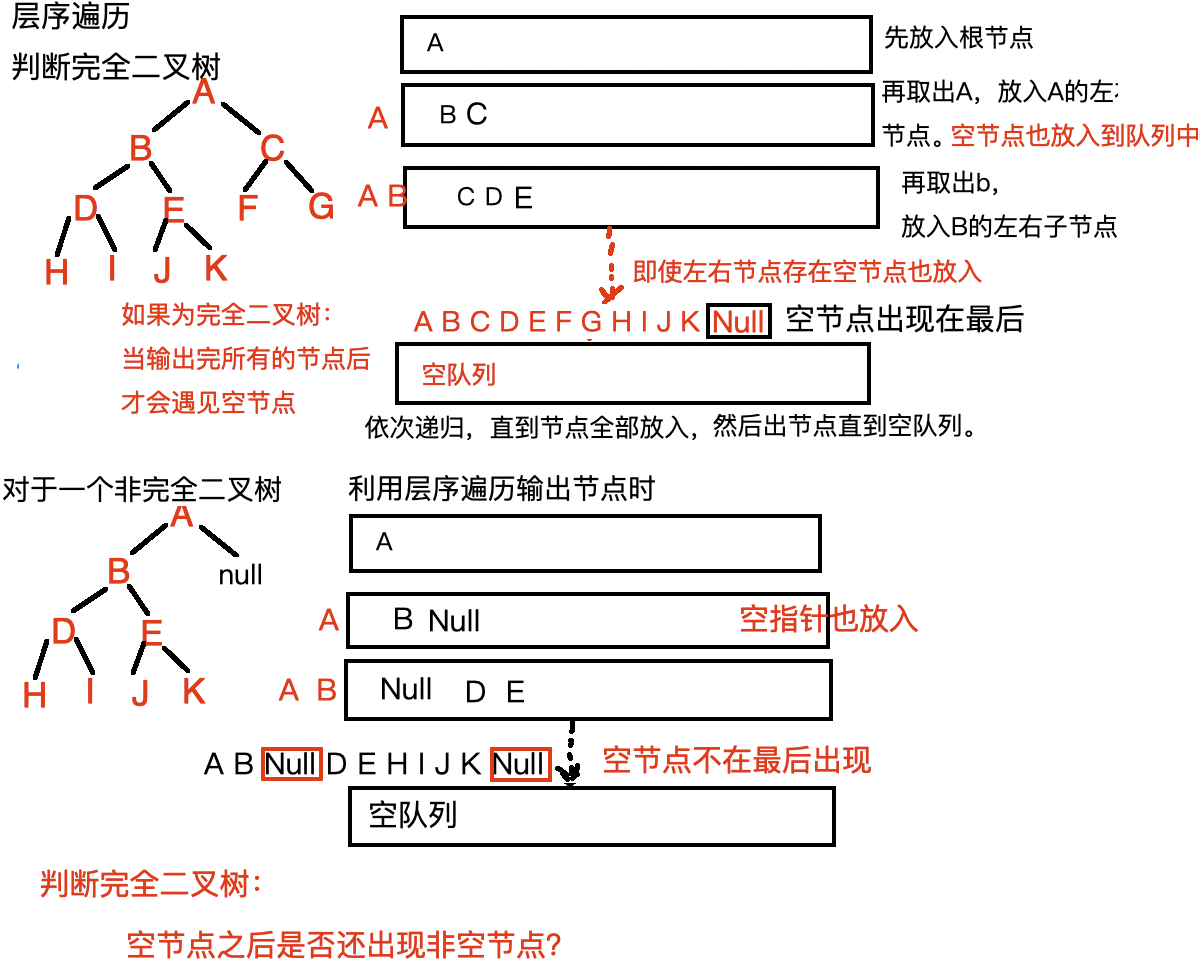
代码实现：

bool IsCompleteTree(BTreeNode* root){if(!root){return true;}my_Queue* BTqueue = Queue_Init();QueuePush(BTqueue,root);bool null_seen = false;while (!IsQueueEmpty(BTqueue)){QueueDataType Front = QueueFront(BTqueue);QueuePop(BTqueue);if(Front == NULL){null_seen = true;}else{if(null_seen){QueueDestroy(BTqueue);BTqueue = NULL;return false;}QueuePush(BTqueue,Front->_left);QueuePush(BTqueue,Front->_right); }}QueueDestroy(BTqueue);BTqueue = NULL;return true;
}

10、测试函数如下：

//测试函数
int main(){char str[100] = {0};scanf("%s",str);int i = 0;BTreeNode* root = CreateTree(str,&i);PreOrder(root);printf("\n");printf("%d ",BTreeSize(root));printf("%d ",BTreeLeafSize(root));printf("%d ",BTreeLevelKSize(root,3));BTreeNode* target = BTreeFind(root,'D');printf("%c ",target->_data);BTree_LevelOrder(root);if(IsCompleteTree(root)){printf("yes\n");}else{printf("No\n");}
}

好了，关于二叉树的c语言相关的内容就分享到这了，后续有关二叉树的内容我们利用c++实现。

谢谢大家的点赞和收藏！👍