传染病监测(六):随机模型 —— 为什么小规模疫情像掷骰子?
开场白:“平均数” 为何会欺瞒?
还记得我们上一篇博客中那个 “每天新增<1 人” 的天花乱坠式预测吗?
倘若你把 100000 人的大城镇换成 10 人的病房,电脑依旧会给出 “平均每天新增 0.8 个人” 的结果 —— 这听起来精确无比,实际却毫无用处:
-
0.8 个人?究竟是 0 个还是 1 个呢?
-
会不会出现今天突然新增 3 个,明天又一个都没有的情况?
-
如果 3 个病人同时接触到同一个小护士,她只会被其中 1 个传染,模型该如何计算这种情况?
这正是 “确定性模型” 的局限所在:它只呈现 “平均剧本”,却忽略了人生中无处不在的意外。
因此,我们今天要请出的嘉宾 ——随机(stochastic)模型,也就是 “看概率的模拟器”。
一、随机模型的 “随机” 之处究竟在哪?
简而言之:把 “人” 真正当作人来看待,而不是当作 “小数”。
它认可三件事:
-
人是整数存在的—— 不存在 0.37 个病人。
-
人生如同抽奖—— 即便传染概率为 20%,也可能一次就被感染,也可能十次都不会被感染。
-
细节影响全局—— 在小群体中,谁和谁一起活动、谁先出现症状,都可能改变整个传染病的传播态势。
二、三种 “概率抽取” 方式,总有一款适用
| 方法 | 昵称 | 核心思想 | 适合场景 | 对电脑要求 |
|---|---|---|---|---|
| 1. Individual-based | “每人一个骰子” | 聚焦每一个个体,逐个通过掷骰子的方式决定其当天是否被感染 | 人数<1000 的小群体,如医院、养老院 | 内存消耗大 |
| 2. Discrete-time compartmental | “一群人的骰子” | 不再关注个体,只关注 “当天会新增几例”—— 一次性抽取一个随机数 | 人数在 1000–10000 人之间 | 中等 |
| 3. Continuous-time (Gillespie) | “等待下一件大事” | 不关注 “今天”,而是关注 “下一分钟还是下一秒会出现新病例” | 任何规模,适合编写代码时使用 | 速度不确定 |
如果你习惯使用 Excel,方法 1 和方法 2 都可以通过拖拽公式来实现;
如果你会使用 R/Python,方法 3 就如同给模型装上了涡轮加速器。
三、实操演示:10 人病房中的流感传播
我们采用方法 1来模拟一次,看看充满 “概率” 的世界是怎样的。
模拟规则
-
病房共有 10 个易感者(Susceptible)。
-
第 0 天加入 1 个传染者(Infectious)。
-
每个人每天只做两件事:要么传染他人,要么第二天获得免疫。
-
传染概率$ p = R_0 / N = 2 / 10 = 0.2 $(即 20%)。
第 1 天:首次 “掷骰子”
给 10 个人各生成一个 0–1 之间的随机数:
| 床位 | 随机数 | 结果 |
|---|---|---|
| 2 号 | 0.0067 | <0.2→被感染,成为传染者 |
| 其余 | >0.2 | 未被感染 |
新增病例:1 例。
病房状态:1 人免疫,1 人发病,8 人处于易感状态。
第 2 天:第二次 “掷骰子”
现在有 1 个传染者,继续对 8 个易感者各进行一次 “掷骰子”—— 结果有 3 个人 “运气不佳”,被感染。
累计病例:1 + 3 = 4 例。
第 3 天:第三次 “掷骰子”
传染者增加到 3 人,被感染的概率飙升至$ 1-(1-0.2)^3 \approx 48.8% $。又新增 4 例。此时病房里只剩 1 个未被感染的人。
第 4 天:模拟结束
最后一个易感者幸运地躲过了 48.8% 的感染概率,模拟结束。总感染人数:1 + 3 + 4 = 8 人。
你在 Excel 中按一下 F9 重新计算,会发现每次的模拟结果都不一样 —— 有时所有人都会被感染,有时只感染 2 人。这就是随机模型的核心:
概率分布比单一结果更能反映真实情况。
四、Reed-Frost 公式:计算小群体传染概率的 “实用工具”
上面提到的$ 1-(1-p)^I $就是著名的Reed-Frost 方程。
它比 “$ \beta \times I $” 更贴合实际:
-
当$ I=1 $时,两者结果相近;
-
当$ I=5 时,时,时, \beta \times I $会错误地显示传染风险为 100%,而 Reed-Frost 方程则表明 “只有 67%,因为一个人不会同时被 5 个人传染 5 次”。
五、模拟多少次才有效?—— 别被 “单次模拟” 误导
随机模型最忌讳 “以偏概全”。
一个实验:针对同一个 10 人病房,分别模拟 20 次、50 次、500 次、2000 次,将最终感染人数绘制成直方图:
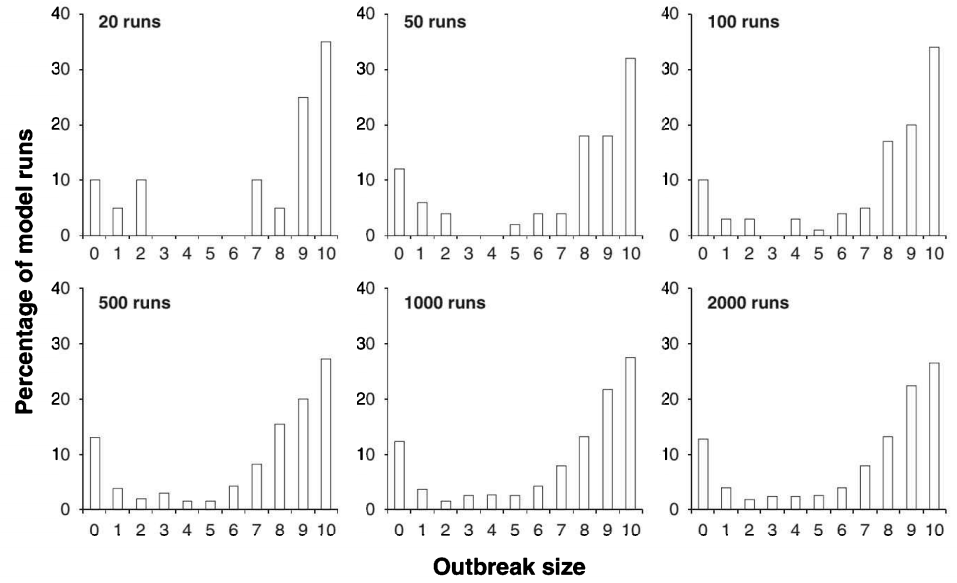
-
模拟 20 次:图形偏差极大,无法得出有效结论。
-
模拟 500 次:图形形状基本稳定,95% 的区间具有可信度。
-
模拟 2000 次:图形几乎没有变化,说明模拟次数足够。
结论:不要用一次模拟的结果去向上级汇报。
日常撰写报告时,至少模拟 500 次;发表 SCI 论文时,模拟 2000 次起步。当然,一个for循环就可以搞定
六、随机模型到底有何用途?三个典型应用场景
-
从疫情暴发倒推
英国在 1995-1998 年记录了 14 起 3–4 人的麻疹暴发、4 起 5–9 人的麻疹暴发、2 起 10–24 人的麻疹暴发以及 1 起≥100 人的麻疹暴发。将这些数据代入公式,反推出净再生数$ R_n \approx 0.5-0.6 $,由此判断 “疫情不会持续传播”,避免了不必要的疫苗恐慌。
-
小岛麻疹的消失与临界人口规模
实际数据显示,人口<25 万的岛屿,麻疹会 “销声匿迹” 几个月,直到有外部输入病例。随机模型计算得出 “临界社区规模” 约为 25–30 万人,与实际观察结果几乎完全一致。
-
医院中的 “手卫生” 影响
某 ICU 通过随机模型模拟 365 天发现,即使每天进行 14 次手卫生,仍有 30% 的模拟会出现 “全年零星感染”、10% 的模拟会出现 “疫情暴发”、60% 的模拟则无感染病例 —— 这告诉院长:不能因为一次无感染就放松警惕,也不能因为一次疫情暴发就撤换主任。
七、给 “想深入学习” 的你
-
想学习方法 1(个体模型)?先尝试使用 Excel 模板(Model6.2),再深入研究 AnyLogic。
-
想学习方法 2(分组建模)?R 语言的
EpiModel包用三行代码就能实现模拟。 -
想学习方法 3(连续时间模型)?
GillespieSSA包加上你的耐心,就能让你掌握这个强大的工具。
一句话总结
确定性模型就像天气预报告诉你 “明天平均降水量 3.7mm”
随机模型则补充说明 “有 20% 的可能下暴雨、10% 的可能无雨,出门既记得带伞也要带防晒”。
