如何在KL散度的意义下解释极大似然估计（二）

MLE和最小化KL散度的等价性

MLE的目标是找到一个参数化的分布 ，使得它在KL散度的意义下最接近真实分布P

step1：最大似然估计的目标函数：

step2：大样本下的期望形式：

step3：KL散度的引入：

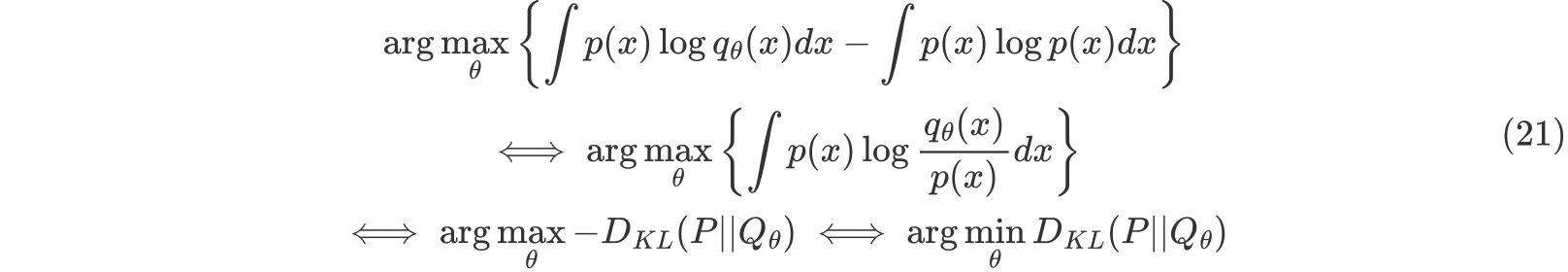
作为损失函数使用

•  分类问题：最小化KL散度等价于最小化交叉熵，因为H(P,Q)-H(P)中H(P)实际上是一个常数，逻辑回归为例

至于为什么逻辑回归不和线性回归一样使用平方损失，是因为sigmoid激活函数下，使用平方损失会导致函数非凸，即使使用梯度下降也很难得到全局最优解

• 通过算法对样本数据进行概率分布建模，那么通常都是使用相对熵KL散度（GAN），因为我们需要明确的知道生成的分布和真实分布的差距，最好的KL散度值应该是0；而在判别模型中，仅仅只需要评估损失函数的下降值即可，交叉熵可以满足要求，其计算量比KL散度小

 为什么二分类问题使用交叉熵损失而不是均方误差损失？

• 统计意义上，最小化交叉熵等价于最大化似然函数，适合概率建模
• MSE在Sigmoid函数下容易导致梯度消失，交叉熵损失可以很好的避免
• MSE做分类任务时会导致 分类错误时 梯度也不更新
• CE求导后，梯度是线性关系，容易计算，适合大规模优化