2025测绘程序设计国赛实战 | 泰森多边形算法C#实现

前言

        本片是针对泰森多边形算法，从基本思路到C#实现，向大家介绍本赛题的解法。有几点需要声明：

1.  数据是简单的二维平面点（比赛的时候如果要上难度，或许就会给你一个经纬度点集，需要先转换到平面）。
2. 无论使用什么语言，比赛时禁用第三方库，请注意。
3. 绘图部分，比赛时不做要求。
4. 本篇无废话，直接上思路和实现代码，比起前面几篇可能稍显粗糙，家人们如有疑问可以私信或评论，我看到会回。

一、数据集＆算法

（一）数据介绍

• 二维平面点集：
  • 每一个点，都是一个种子点。

（二）Bowyer-Watson 算法

//本部分只介绍了这个算法设计的核心过程，当然我们在处理三角网边界、处理邻接关系、处理共线情况···都需要实现对应的方法。

• def：一种构建Delaunay 三角网(把点连接成三角形，每个三角形的外接圆不包含其他点)的方法。
• 步骤：

  • 先画一个超级大的三角形（把所有点先包含进去，程序代码如下）

Point superP1 = new Point("左下", -1e5, -1e5);
Point superP2 = new Point("右下", 1e5, -1e5);
Point superP3 = new Point("上", 0, 1e5);
Triangle superTriangle = new Triangle(superP1, superP2, superP3);

•  一个一个地 "扔" 点进去。

• 找到 "坏三角形"：每次扔一个点后，检查哪些三角形的外接圆包含了这个新点。这些三角形就是 "坏三角形"，因为它们不符合 Delaunay 三角网的规则。

foreach (var p in points)
{// 找出所有外接圆包含p的三角形（坏三角形）List<Triangle> triangles_bad = triangles.FindAll(tr => judge_inCircle(tr, p));// ...
}

• 拆掉坏三角形，形成一个 "洞"：把所有坏三角形都删掉，这样就会在原来的三角网中形成一个 "洞"。这个洞的边界是由一些线段组成的，这些线段叫做凸包边。

•  用新点和凸包边形成新的三角形：现在，你要把这个新点和凸包边的每个线段连起来，形成新的三角形。这样就把 "洞" 补上了，而且新的三角形满足 Delaunay 条件。

// 用凸包边和新点形成新的三角形
foreach (var edge in polygon)
{triangles.Add(new Triangle(edge.Item1, edge.Item2, p));
}

• 最后，把超级三角形相关的三角形删掉：这是最后一步，把最开始画的超级大三角形以及和它相连的三角形都删掉，因为它们不属于我们真正的点集。这样就得到了只由输入点构成的 Delaunay 三角网。

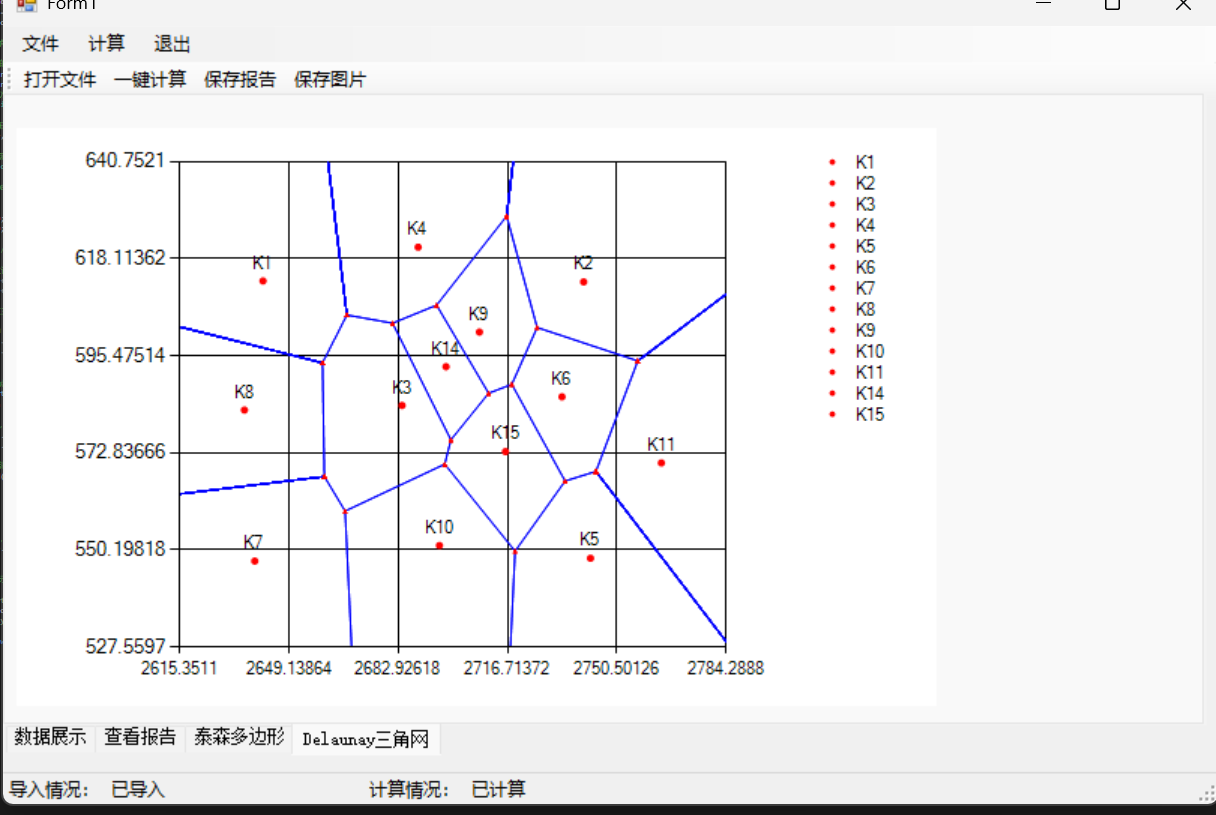
（三）泰森多边形构建

• def：泰森和Delaunay三角网，就是一种双生关系（AI说是对偶关系）。泰森多边形也叫Voronoi 图，简单说就是把平面划分成多个区域，每个区域包含一个点，并且区域内任意位置到这个点的距离都比到其他点的距离近。
• 步骤：
  • 在Delaunay三角网构建完毕的基础上，先找到每个三角形的外心。（这个直接在定义数据结构的时候，就为三角形结构体附上外心属性。写程序，知道数据是怎么流动的，真的很重要。）

  • 连接相邻三角形的外心：如果两个三角形共享一条边，那么它们就是相邻的。把相邻三角形的外心连起来，就形成了泰森多边形的边。

  • 处理边缘三角形：边缘的三角形只有一个相邻三角形，它们的泰森多边形边界是一条射线，指向无穷远。在程序中，我们用一条足够长的线段来表示这条射线。

（四）总体思路

1. 窗体设计
2. 数据读取（这个很常规了，基本操作）
3. 建立数据结构（点、三角形）
4. 算法实现
   1. 先通过 Bowyer-Watson 算法构建 Delaunay 三角网
   2. 再从三角网的外心生成泰森多边形。
5. 可视化（不必须，比赛不要求画图）

二、C#实现

（一）窗体设计

//哈哈，小编说了会沿用地图图幅计算和GNSS的界面风格，属实是说到做到了哈哈

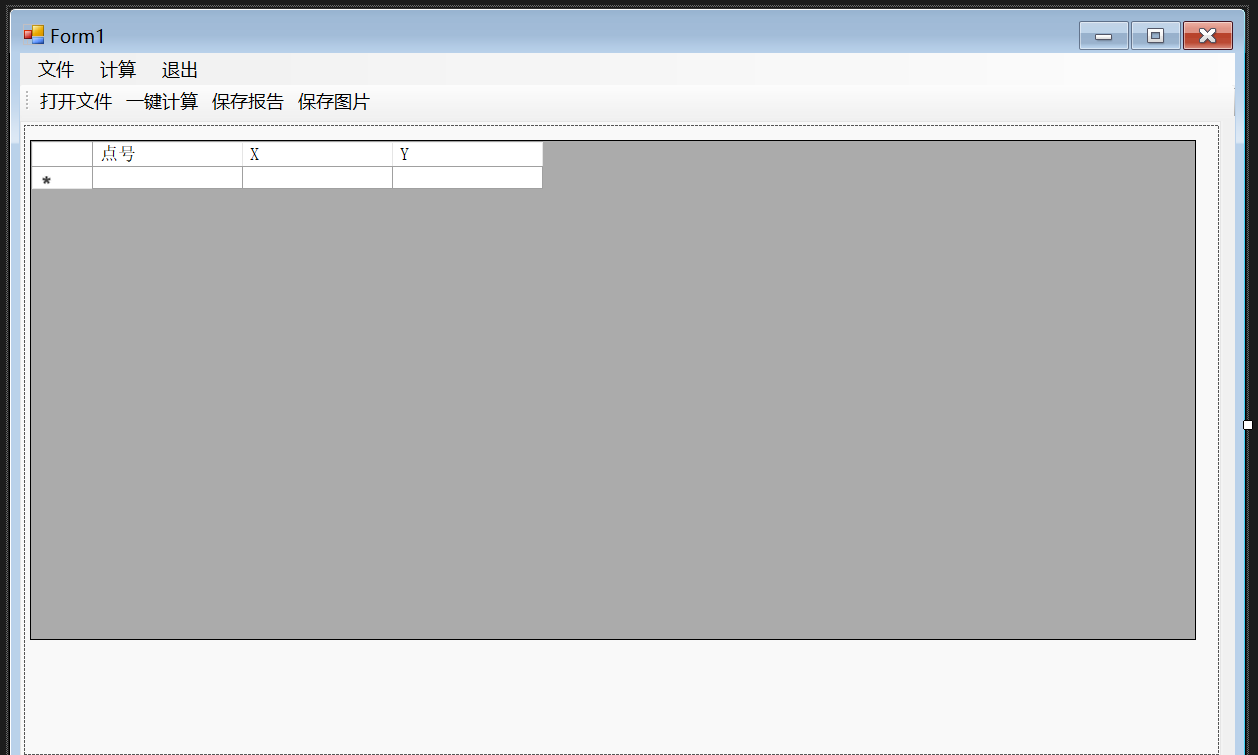
（二）数据结构

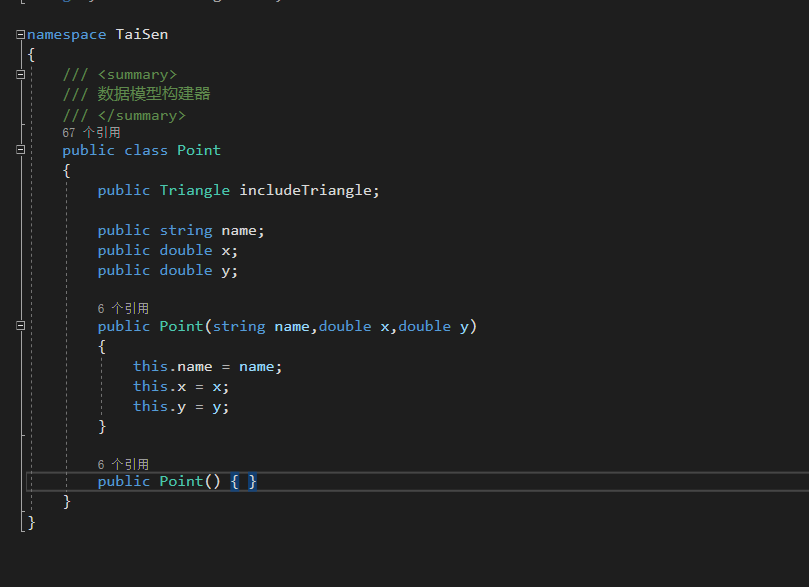
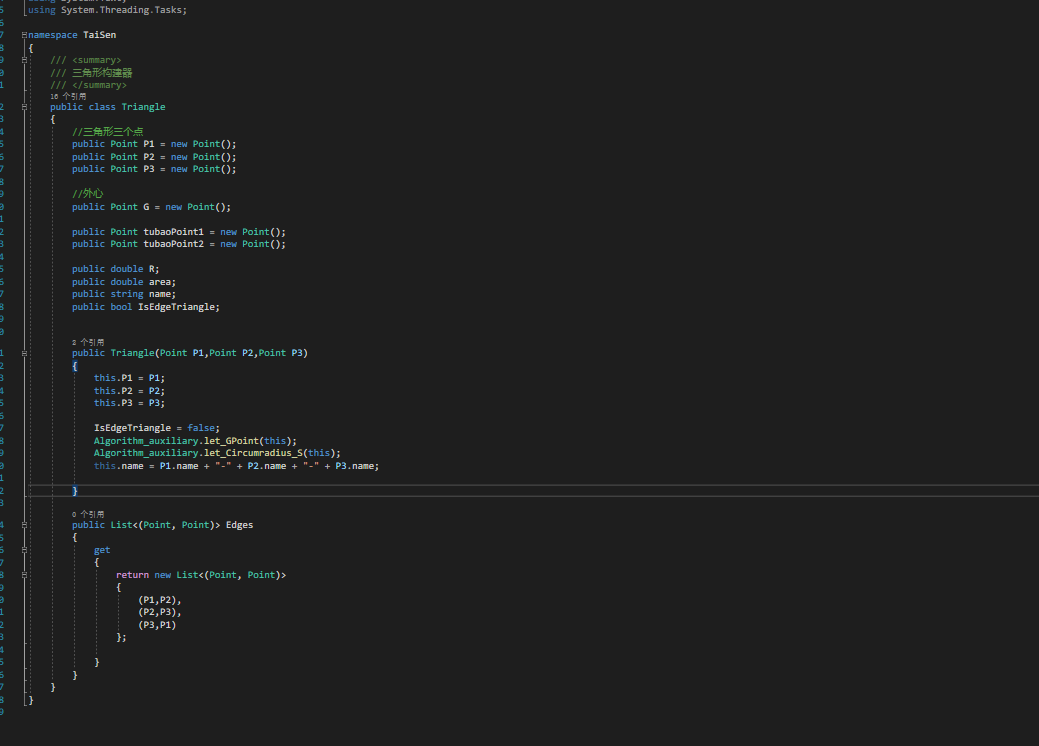
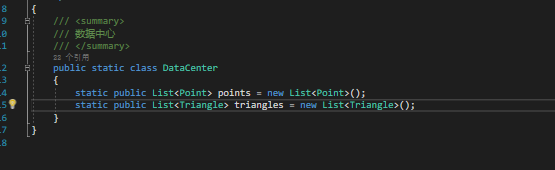（这招也是学习得得来的）

（三）文件管理

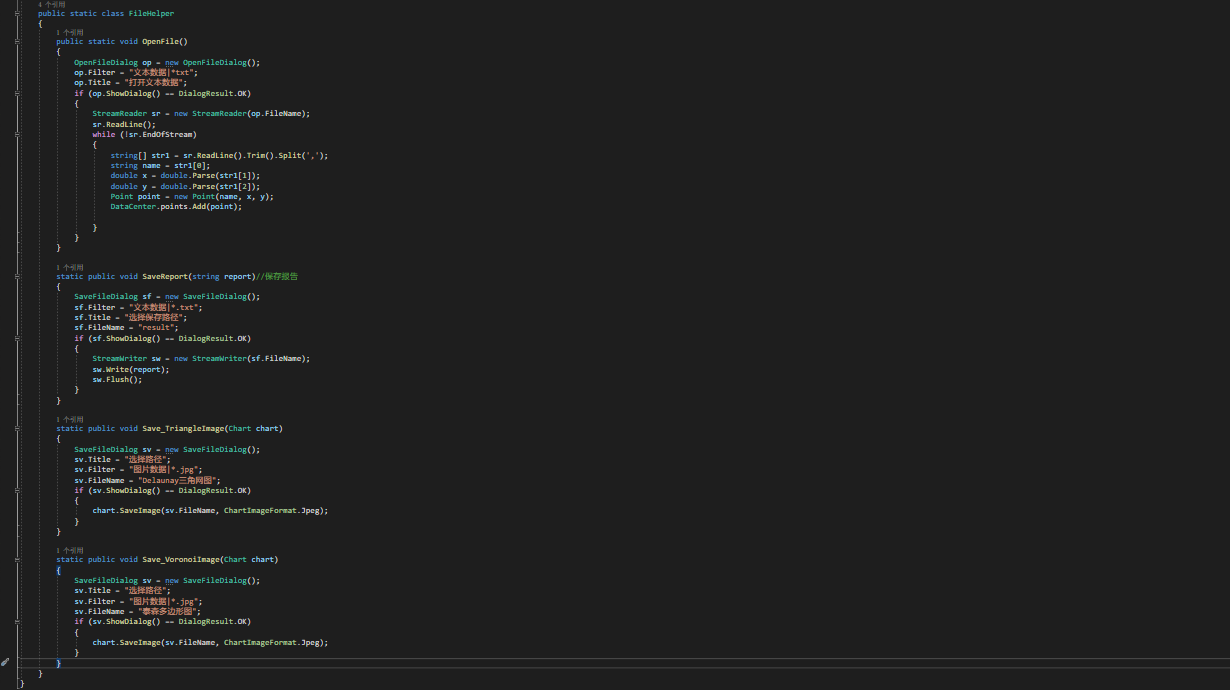
（四）核心算法

//分了两个类，一个放辅助，一个具体实现

• 辅助

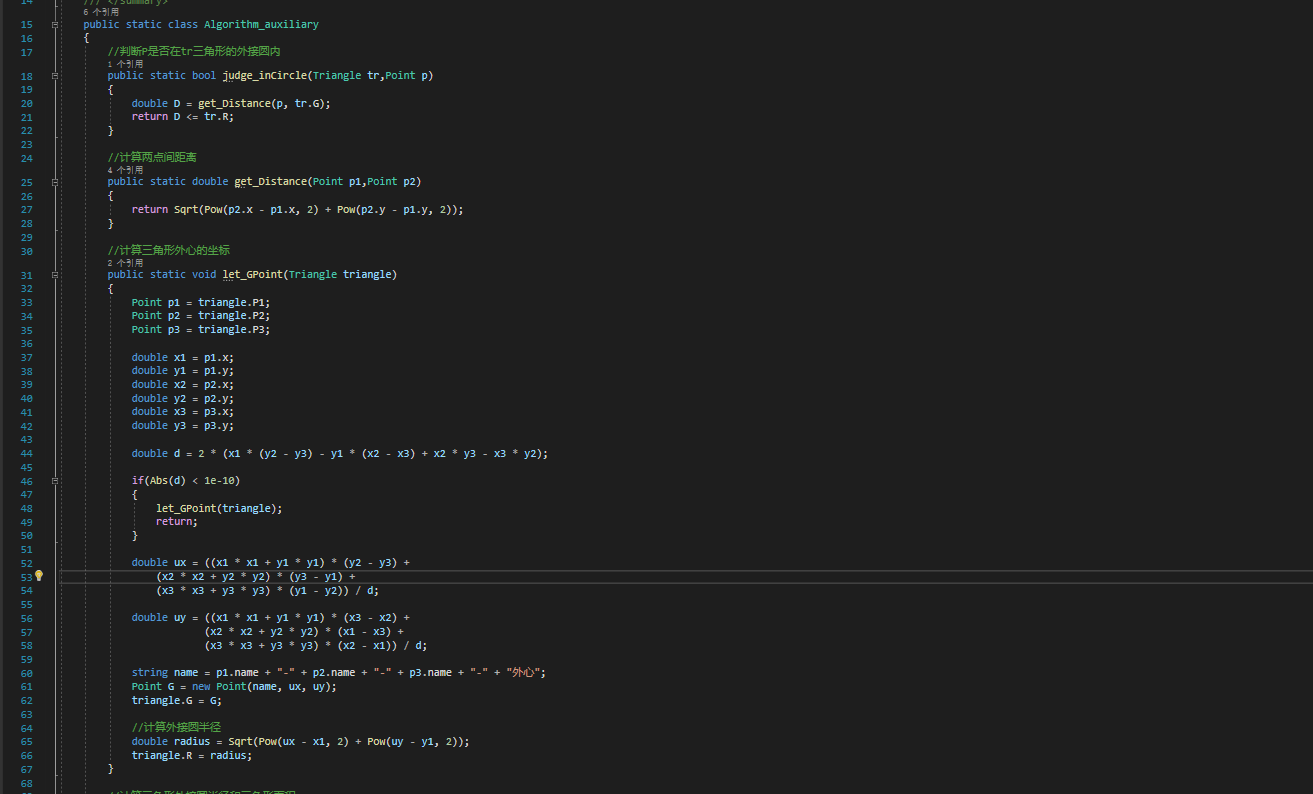
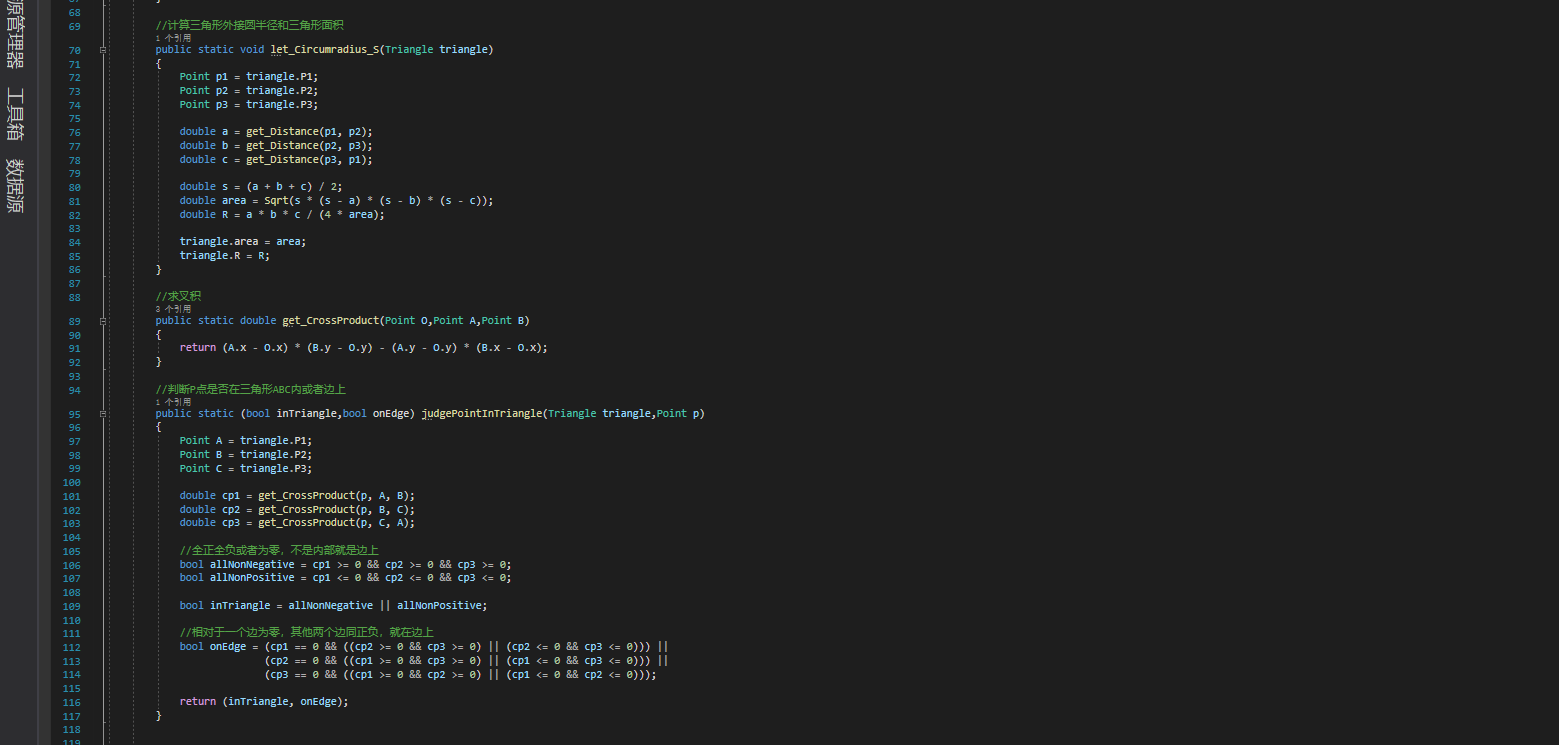
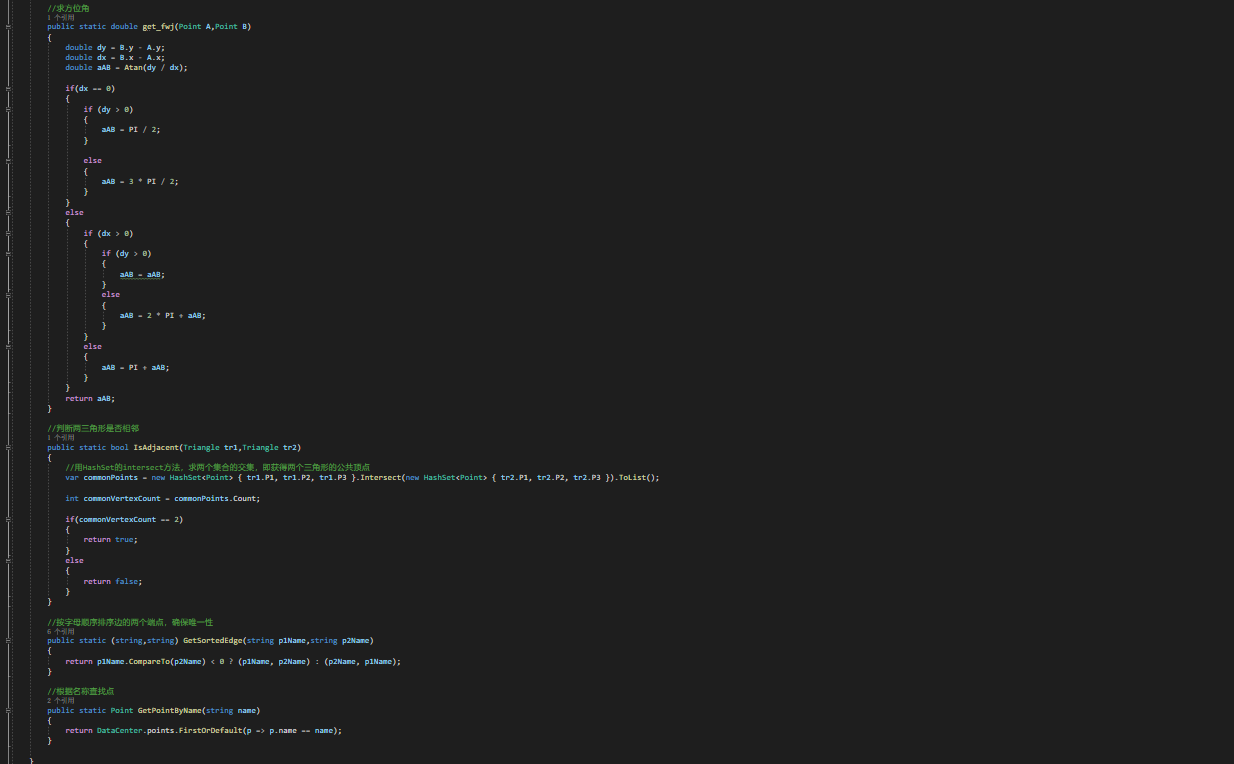
• 核心

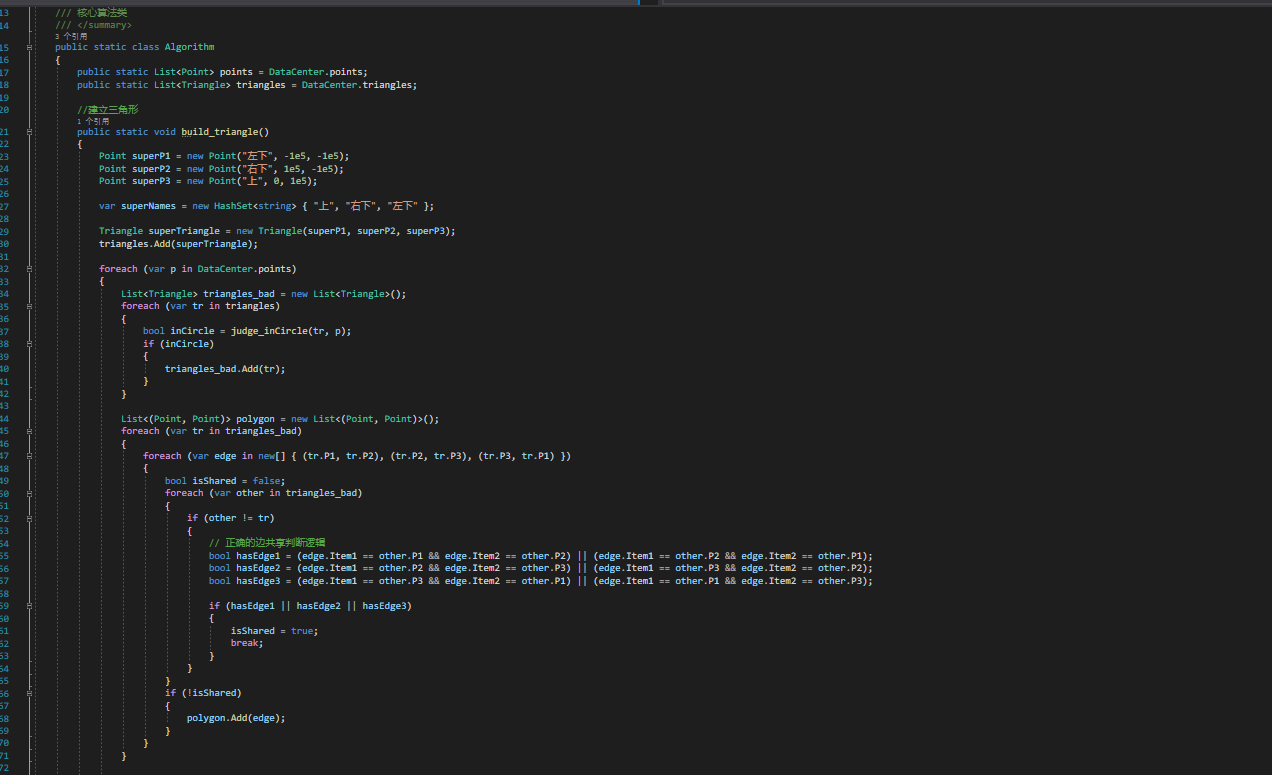
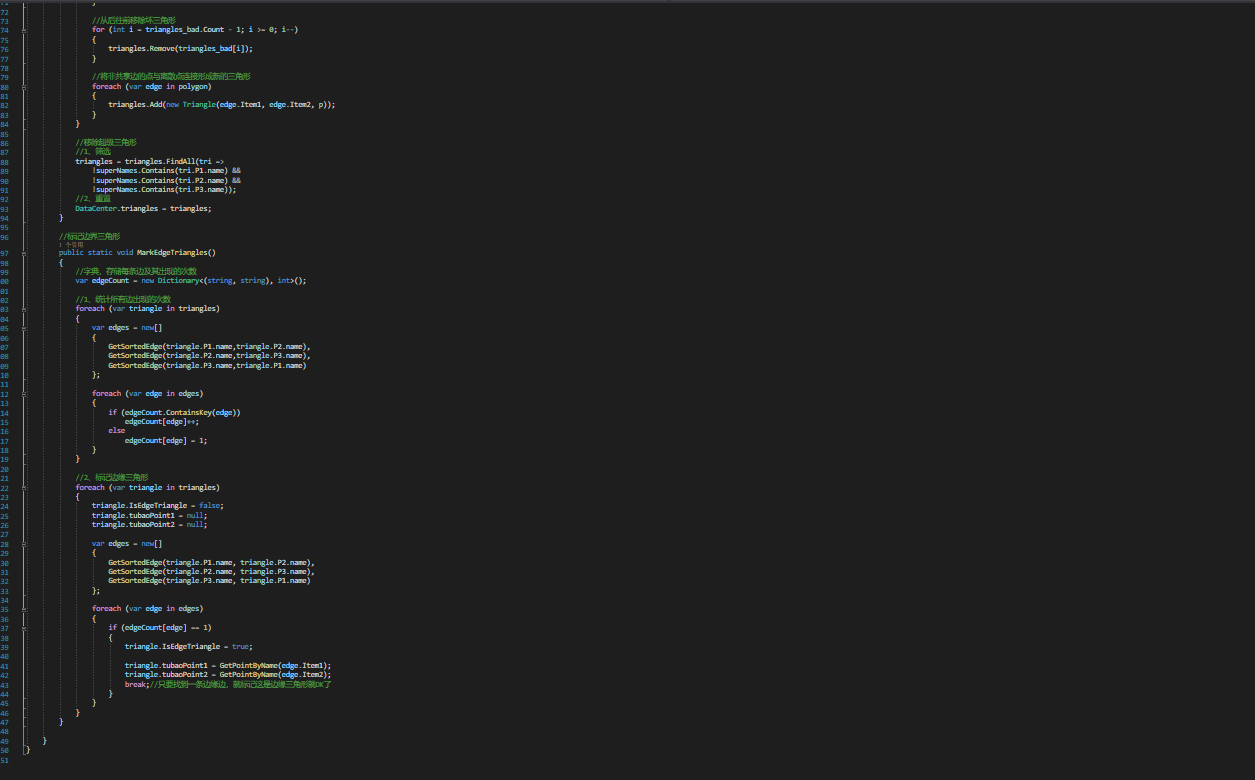
（五）可视化Draw

//比赛可视化，就纯是我们附赠产品。

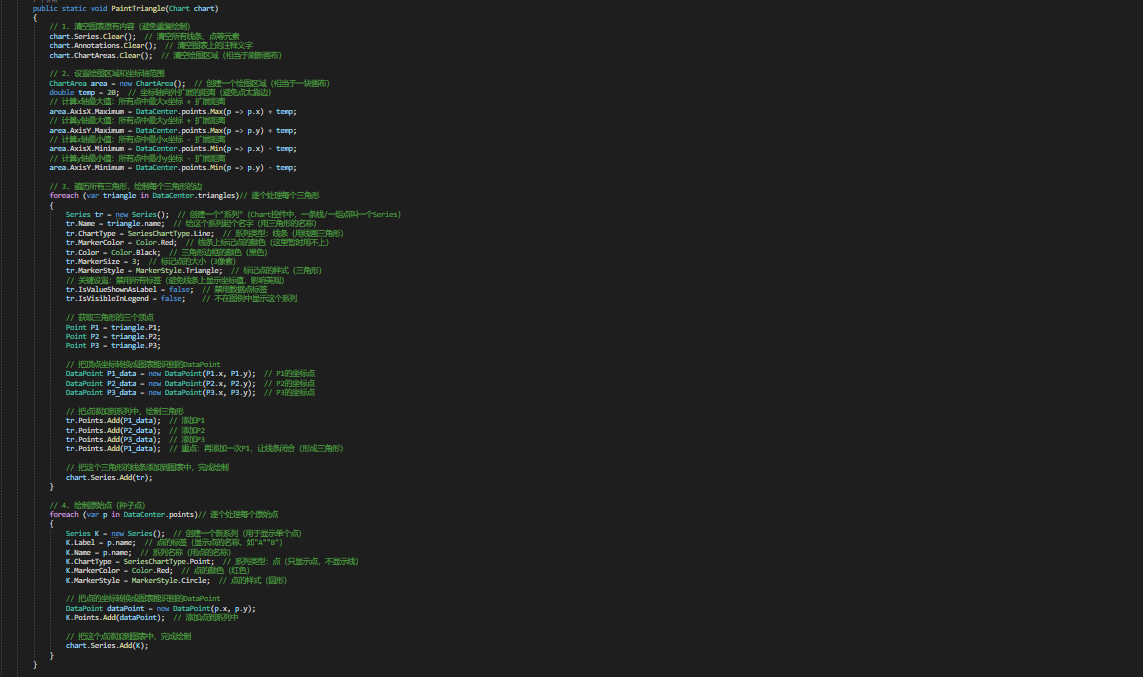
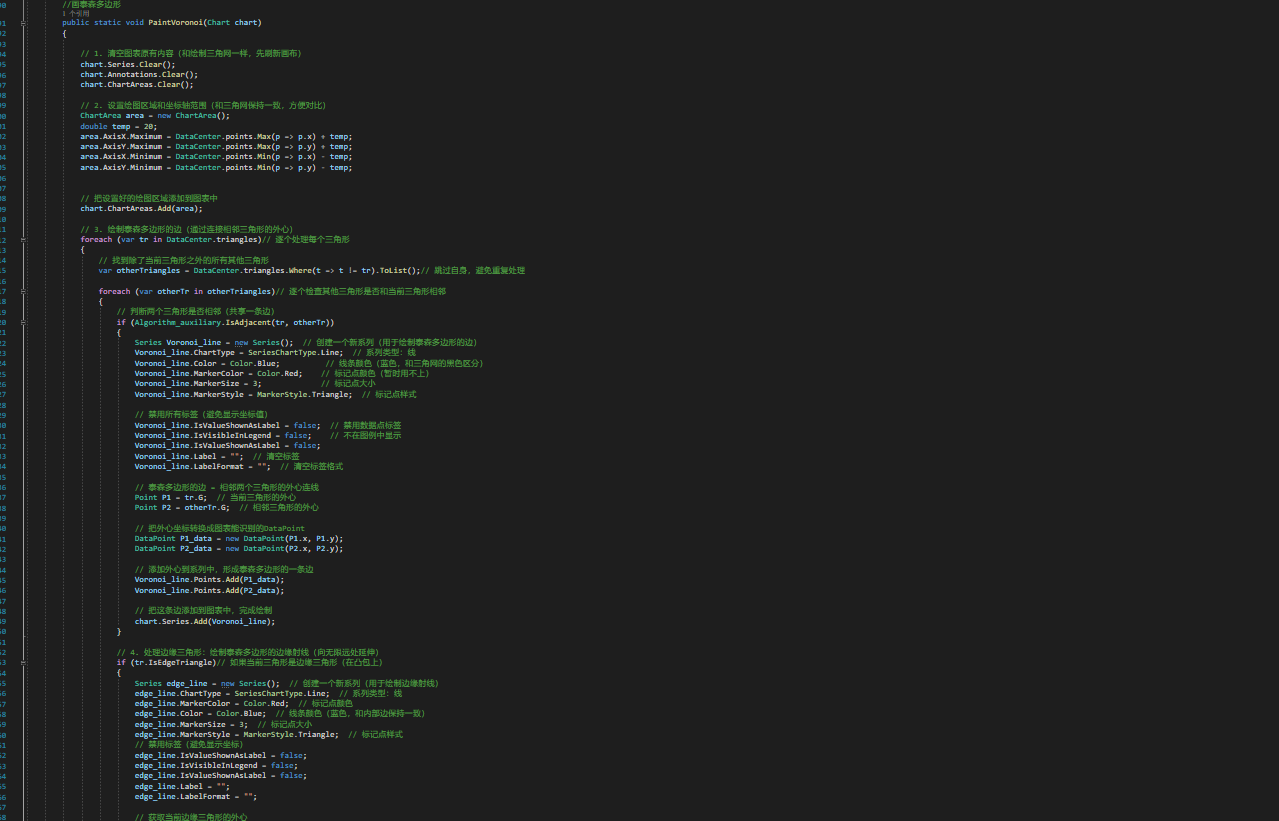
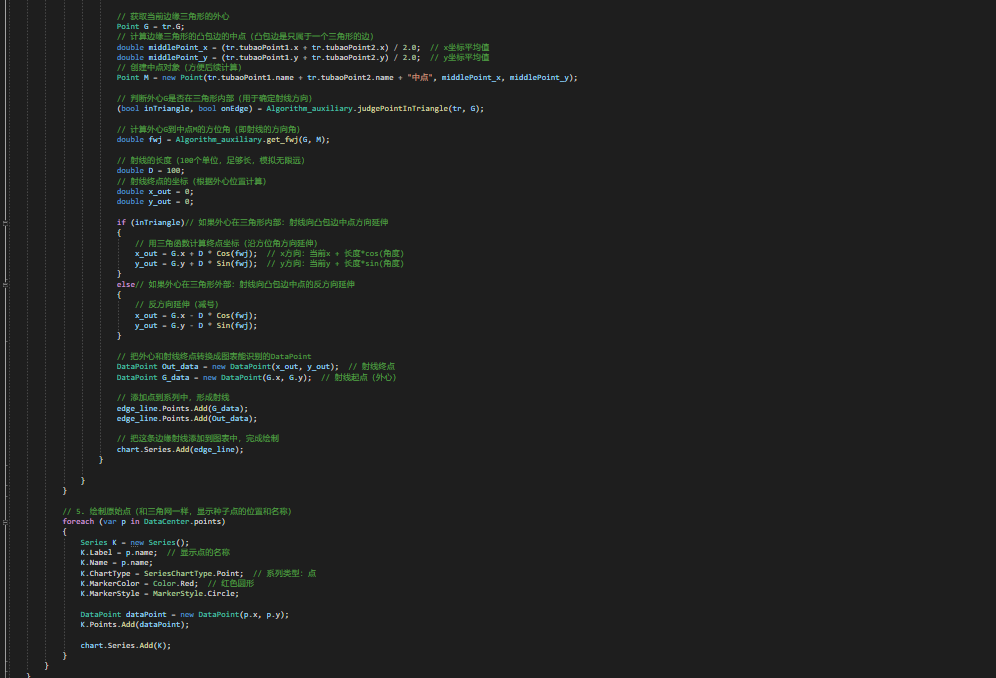
三、结果