魔术公式轮胎simulink模型建立及参数拟合
一、魔术公式说明(详情见参考文献文件夹内资料)
1.1魔术公式概述
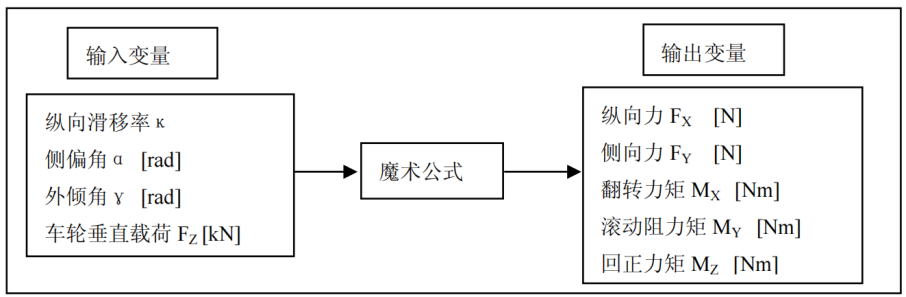
魔术公式是⽤三⻆函数的组合公式拟合轮胎试验数据,⽤⼀套形式相同的公式就可以完整地表达轮胎的纵向⼒Fx、侧向⼒Fy、回正⼒矩Mz、翻转⼒矩Mx、阻⼒矩My以及纵向⼒、侧向⼒的联合作⽤⼯况,故称为“魔术公式”。魔术公式的一般表达式:
![]()
式中y(x)可以是侧向力,也可以是回正力矩或者纵向力,自变量x可以在不同的情况下分别表示轮胎的侧偏角或纵向滑移率,式中的系数B、C、D依次由轮胎的垂直载荷和外倾角来确定。应用“魔术公式”的一般表达式可以建立轮胎的纵向力、侧向力和回正力矩的数学模型,完整地表达轮胎的力学特性。
1.2轮胎纵向力计算公式
纯滑移工况下(即纯制动或纯驱动且无转弯的工况)纵向力计算公式:

1.3轮胎侧向力计算公式
纯侧偏工况下(即纯转弯)侧向力计算公式:

1.4联合工况下轮胎力计算
在联合工况下轮胎纵向力Fx与侧偏力Fy分别与轮胎侧偏角α、纵向滑移率λ和垂直载荷Fz之间的关系为:
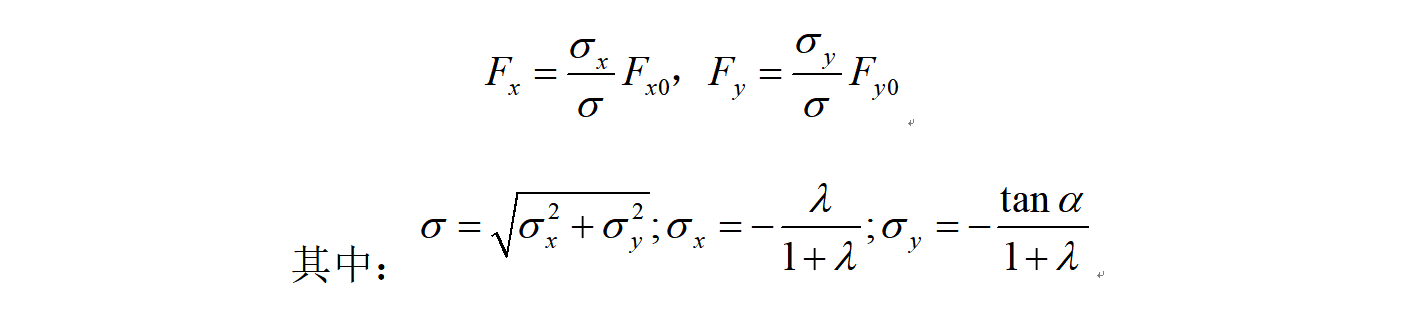
二、使用Curve Fitting拟合魔术公式参数
在知道魔术公式轮胎模型的数学表达式之后便可以通过轮胎数据拟合出A0,A1...A10,B1,B2...B10等参数。
轮胎数据获取:打开carsim的轮胎页面后,点击Excel会弹出轮胎数据的Excel文件,将文件另存一份作为拟合的数据
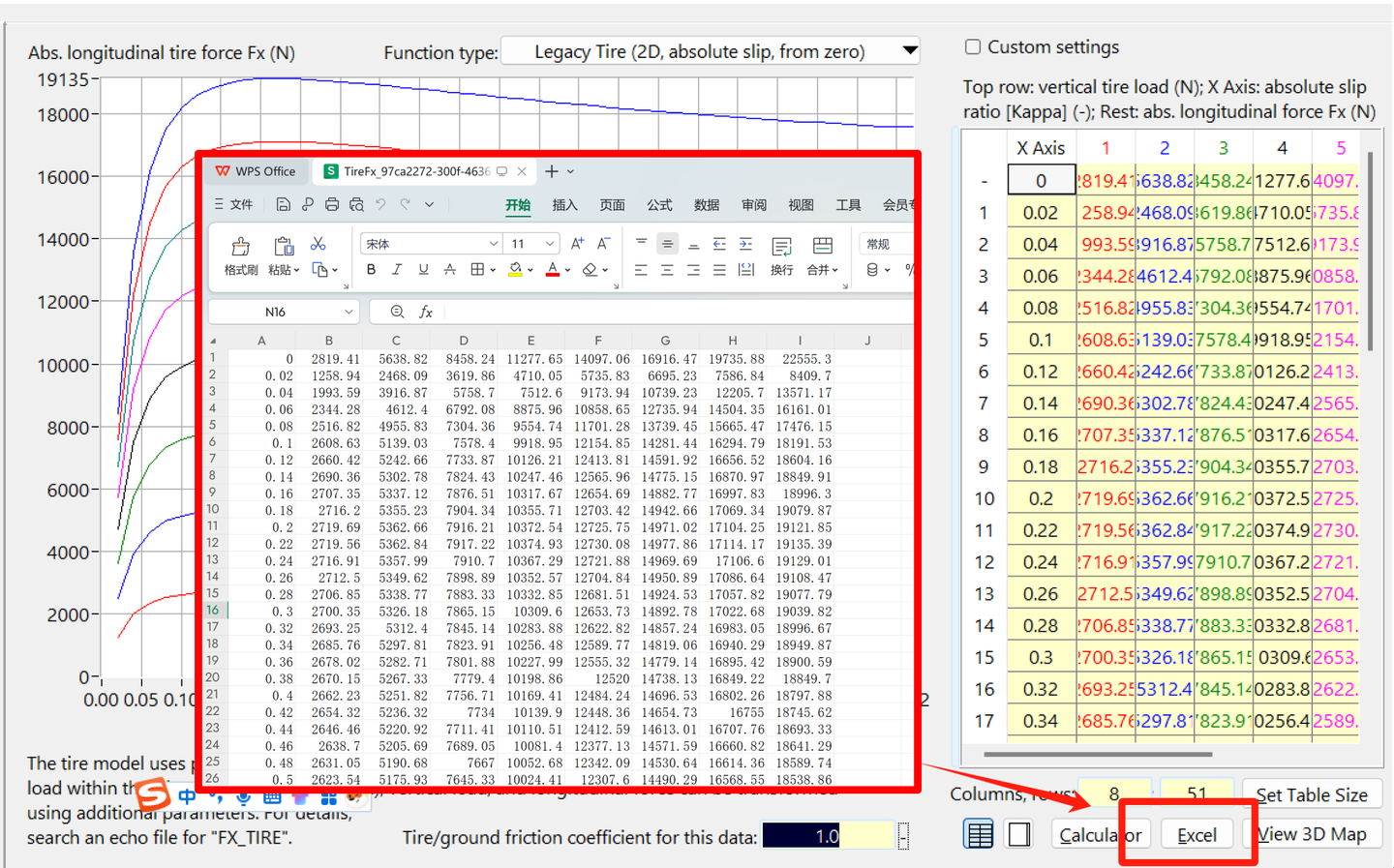
注意这里需要对另存后的文件进行修改,确保曲线经过(0,0)原点
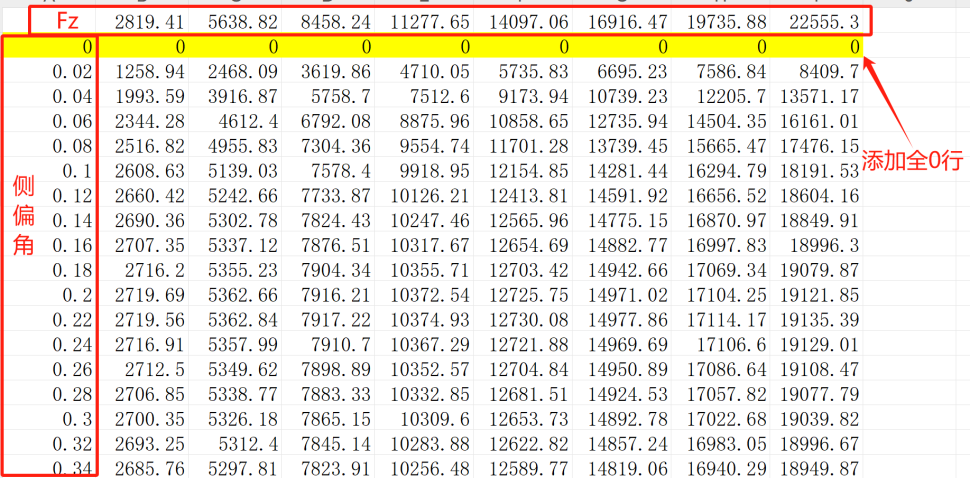
数据导入:打开Matlab将保存的轮胎数据导入至Matlab工作区中以备拟合使用,使用xlsread函数可以将Excel内数据以矩阵形式赋于定义的变量。并创建轮胎里Fx,Fy,Fz,滑移率lamda和侧偏角alpha等变量
%% 将事先准备好的carsim轮胎excel数据导入
[x]=xlsread('C:\Users\16565\Desktop\流浪麦当劳\车辆知识分享\simulink模型分享\魔术公式轮胎(模型+参数拟合)\235_55_R18轮胎数据(纵向).xlsx');
[y]=xlsread('C:\Users\16565\Desktop\流浪麦当劳\车辆知识分享\simulink模型分享\魔术公式轮胎(模型+参数拟合)\235_55_R18轮胎数据(侧向).xlsx');
Fz=x(1,2:end);%垂直载荷
lamda=x(2:end,1);%滑移率
Fx=x(2:end,2:end);%纵向力
alpha=y(2:end,1);%侧偏角
Fy=y(2:end,2:end);%侧向力导入好的数据如下图所示:
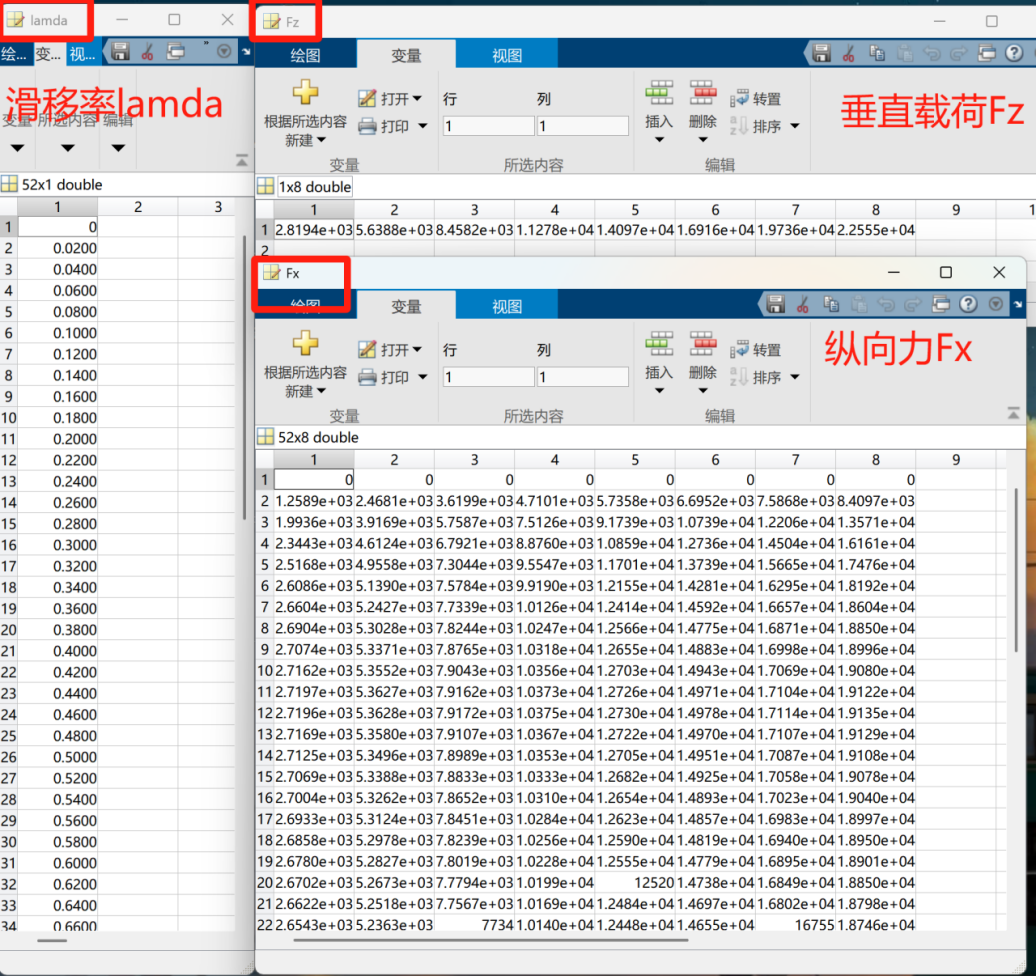
数据拟合:Matlab的曲线拟合工具箱可以根据的数据拟合出输入和输出的关系曲线,同时支持用户自定义拟合关系式进行拟合,故我们用可以Curve Fitting+轮胎数据+魔术公式表达式拟合相关参数。打开曲线拟合工具箱,并配置X,Y,Z,其中X和Y作为输入,Z为输出,故令X为滑移率lamda或侧偏角alpha
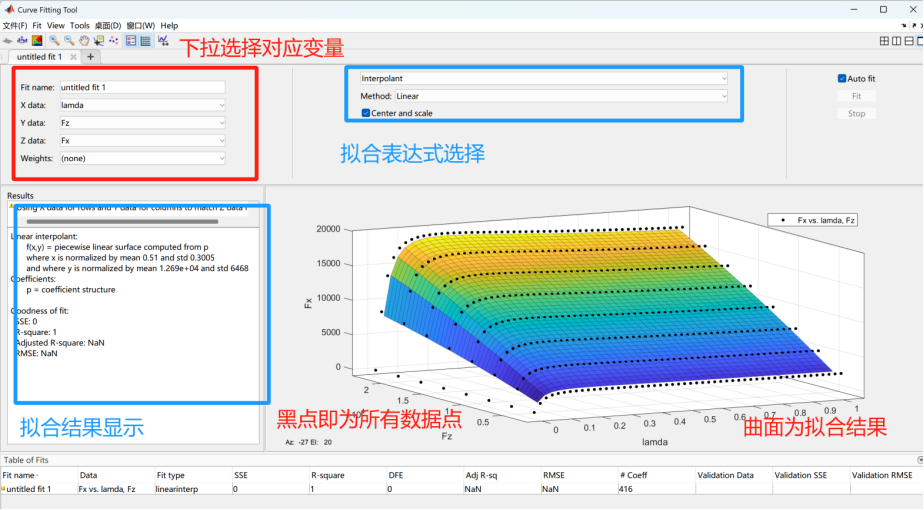
选择用户自定义方程,并输出魔术公式表达式:
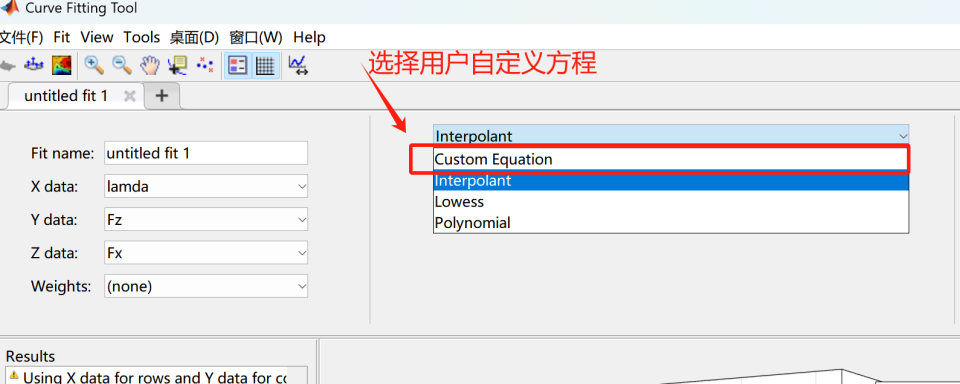
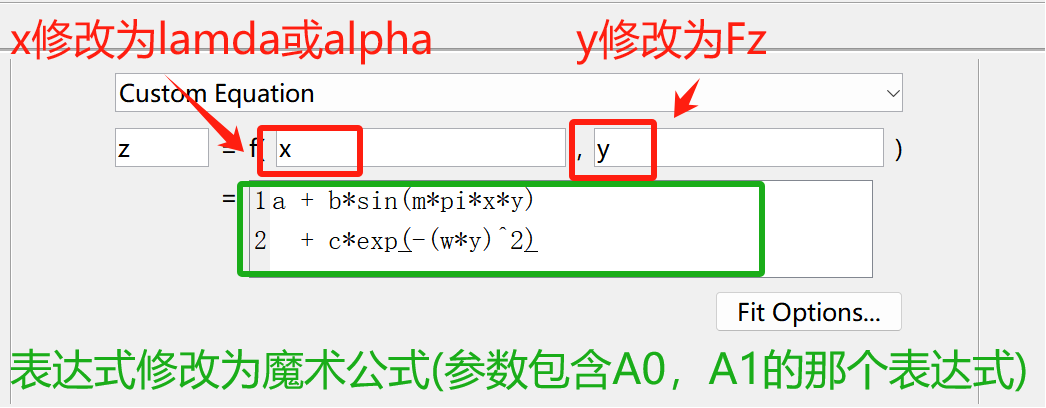
魔术公式的完整表达式如下,可直接复制进去即可:
Fx_fit=((a1.*Fz.^2+a2.*Fz)).*sin(a0.*atan((((a3.*Fz.^2+a4.*Fz).*exp(-a5.*Fz))./(a0.*(a1.*Fz.^2+a2.*Fz))).*(lamda) - (a6.*Fz.^2+a7.*Fz+a8).*((((a3.*Fz.^2+a4.*Fz).*exp(-a5.*Fz))./(a0.*(a1.*Fz.^2+a2.*Fz))).*(lamda) - atan((((a3.*Fz.^2+a4.*Fz).*exp(-a5.*Fz))./(a0.*(a1.*Fz.^2+a2.*Fz))).*(lamda)))));Fy_fit = (b1.*Fz.^2+b2.*Fz).*sin((b0).*atan(((b3.*sin(2.*atan(Fz./b4)).*(1-b5.*camber))./(b0.*(b1.*Fz.^2+b2.*Fz))).*alpha-(b6.*Fz+b7).*(((b3.*sin(2.*atan(Fz./b4)).*(1-b5.*camber))./(b0.*(b1.*Fz.^2+b2.*Fz))).*alpha-atan(((b3.*sin(2.*atan(Fz./b4)).*(1-b5.*camber))./(b0.*(b1.*Fz.^2+b2.*Fz))).*alpha))));
如果顺利没有报错的话,第一次拟合出的结果有可能出现类似图中的结果,拟合结果很差
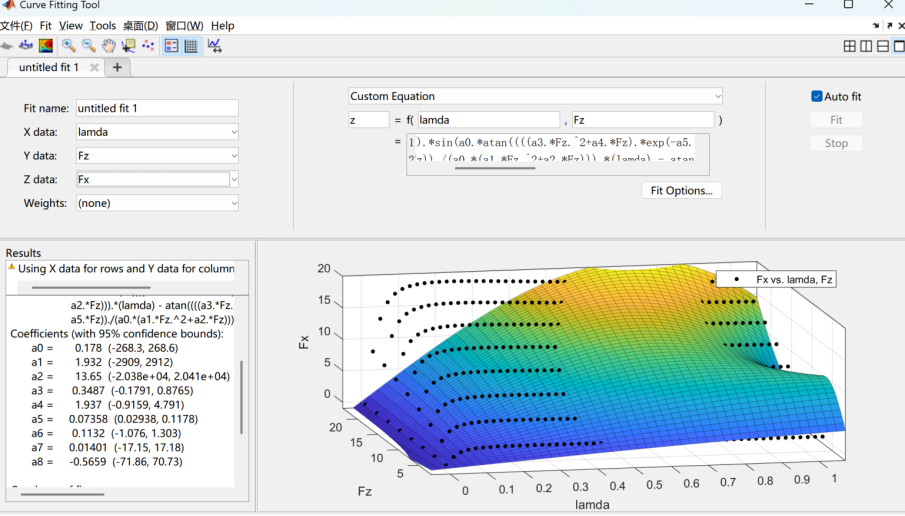
这里我怀疑过是公式打错了,或者是数据单位的问题但最后发现这两个都没有问题,在经过一个晚上的试错,最后发现在数据和拟合表达式完全相同的情况下,每次的拟合结果都不一样(这里可以自己尝试一下,点击XYZ data重新选择一遍,拟合曲面会刷新一遍并得到新的拟合结果,视频为证:视频链接),之所以每次捏合结果不同是因为我们没有为拟合参数的初始值赋值,所以每次拟合的参数是从一个随机的起点开始拟合。
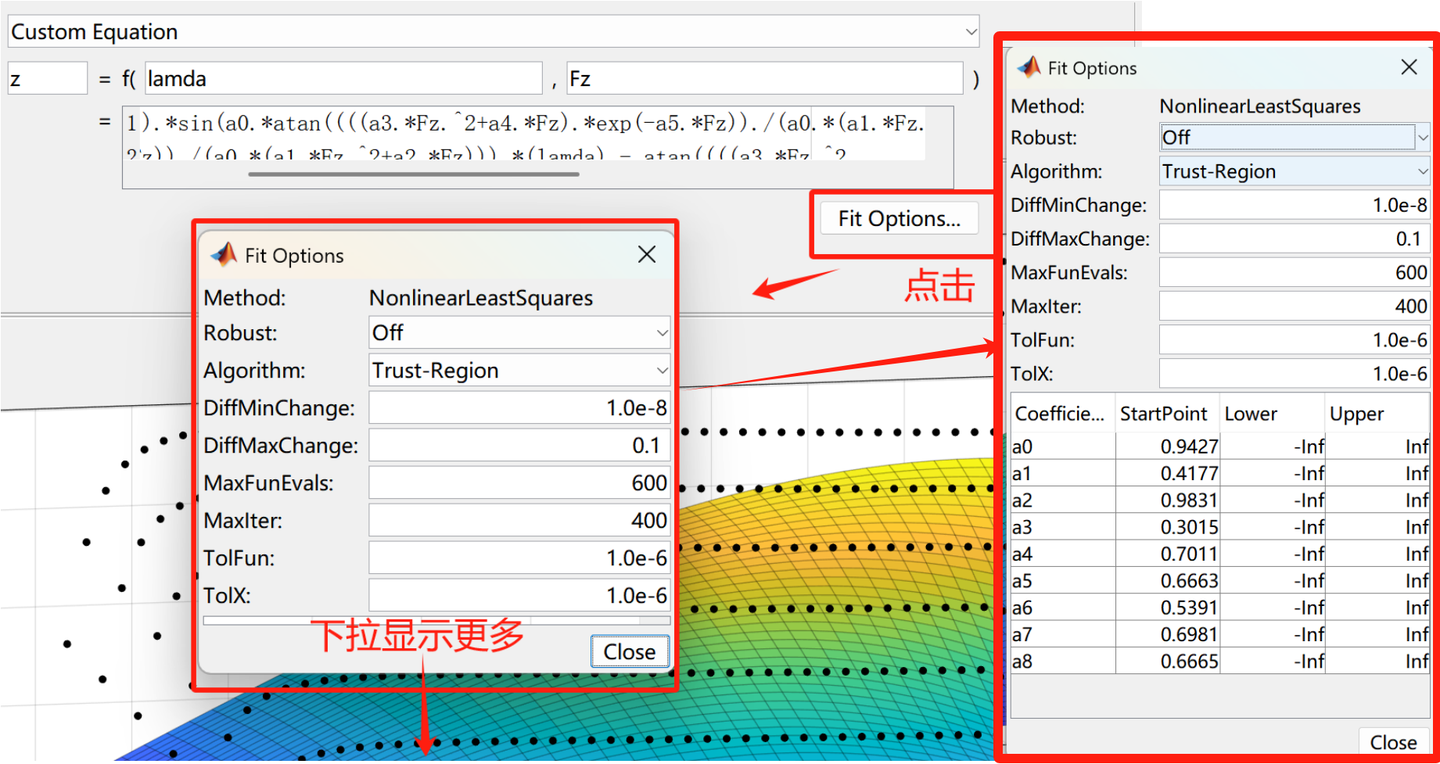
个人理解,最优的拟合结果对应着一套最优的拟合参数,而每次拟合的过程就是参数从起始点的值向最优参数值逼近的过程,不过这个逼近的迭代次数再一次拟合过程中是有限的,初始值越接近最优点拟合的结果越好。
那么在不知道最优点的情况下如何设置起始地呢?我这里采用的方法是将每一次拟合的参数结果作为下一次拟合的起始点,这样就可以一点点向着最优拟合参数逼近。(这里建议将上一次拟合的参数截图然后将a0~a1的起始点一起更改,因为改变一个参数的初始点会重新拟合,这样参数的起始点又乱掉了)
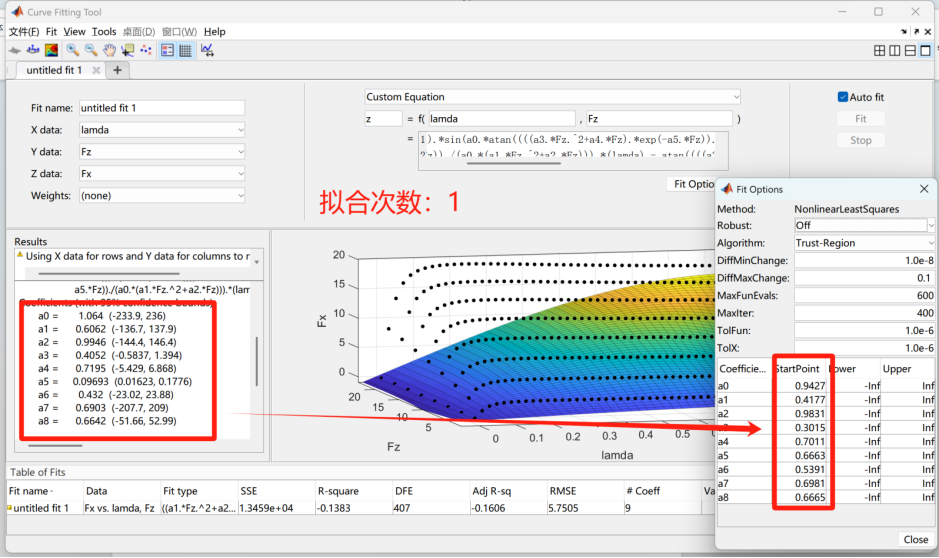
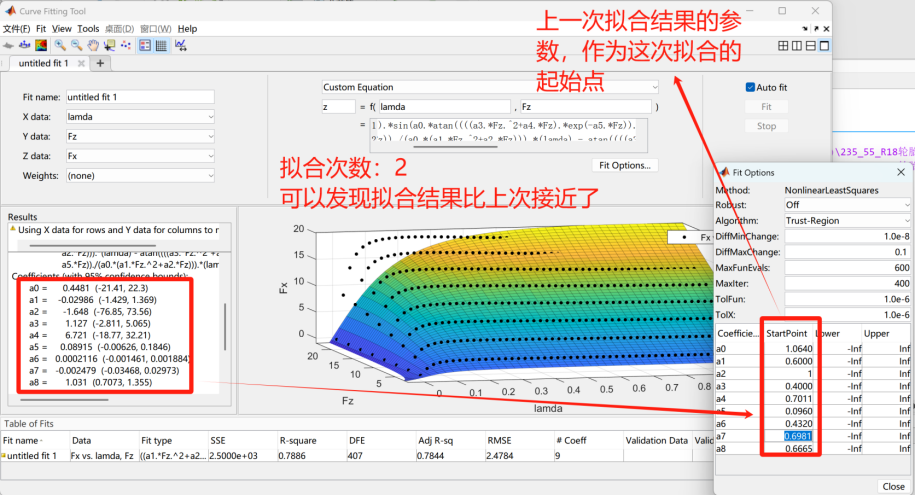
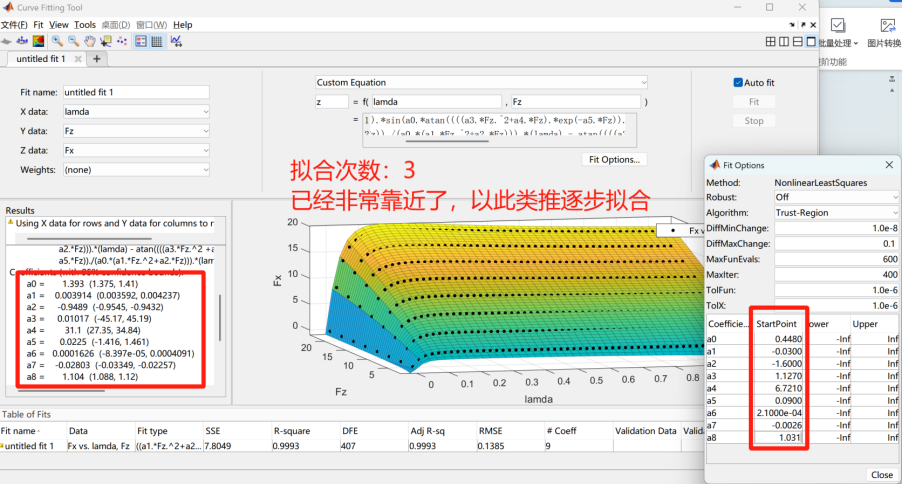
通过多次逐步逼近的拟合,最终得到一组拟合参数可以作为魔术公式的参数来计算轮胎力。最后通过matlab的plot绘图将carsim的轮胎力和魔术公式计算的轮胎力进行比较,代码实现如下:
%%
%%拟合得到的参数如下
%纵向轮胎力特性
a0=1.399;
a1=-0.006249;
a2=0.9901;
a3=-0.4101;
a4=24.68;
a5=-0.01204;
a6=-0.0002904;
a7=0.009179;
a8=0.6324;
Fx_fit=((a1.*Fz.^2+a2.*Fz)).*sin(a0.*atan((((a3.*Fz.^2+a4.*Fz).*exp(-a5.*Fz))./(a0.*(a1.*Fz.^2+a2.*Fz))).*(lamda) - (a6.*Fz.^2+a7.*Fz+a8).*((((a3.*Fz.^2+a4.*Fz).*exp(-a5.*Fz))./(a0.*(a1.*Fz.^2+a2.*Fz))).*(lamda) - atan((((a3.*Fz.^2+a4.*Fz).*exp(-a5.*Fz))./(a0.*(a1.*Fz.^2+a2.*Fz))).*(lamda)))));
%作图对比,按照拟合参数计算得到的Fx_fith和carsim轮胎的Fx进行对比
figure(1)
s1=plot(lamda,Fx,'color','red','LineStyle','-','linewidth',1.5);
hold on
s2=plot(lamda,Fx_fit,'color','blue','LineStyle','-.','linewidth',1.5);
legend([s1(1),s2(1)],'Carsim','fit',Orientation='horizontal')
set(gca,'FontSize',10,'FontWeight','bold', 'FontName','Times','XTick',(0:0.1:1),'YTick',(0:2:30),'xlim',[0,1],'ylim',[0,22]);
xlabel('\fontname{宋体}滑移率');
ylabel('\fontname{宋体}Fx\fontname{Times new roman}(kN)');
title('\fontname{宋体}MF纵向力拟合对比图');对比结果如图所示:
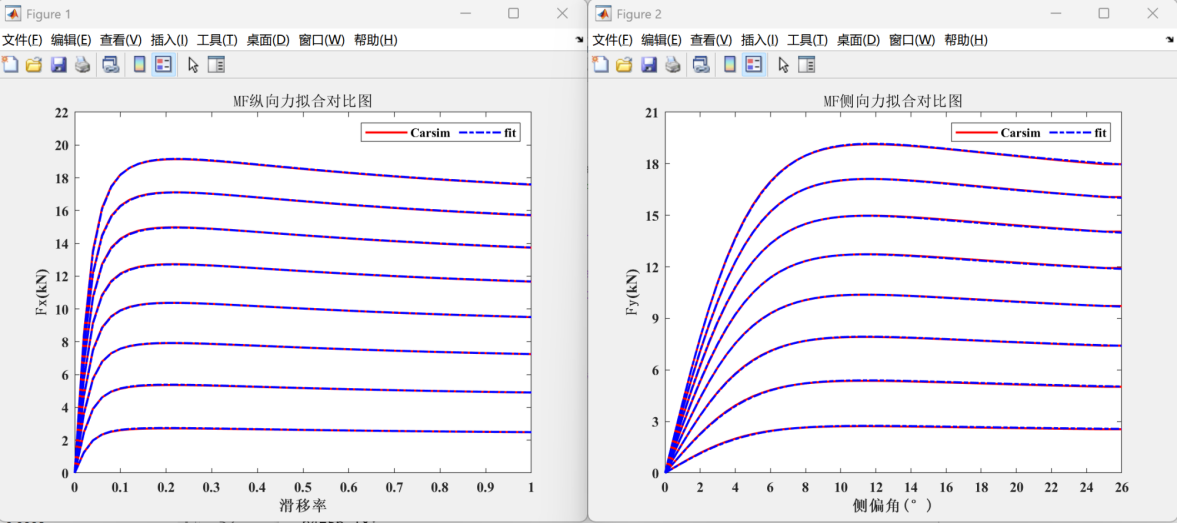
可以看出拟合的非常成功。^_^
