Codeforces Round 1016 (Div. 3) A-F

A. Ideal Generator

题目大意

一个数字k是理想的生成器，如果对于任意一个数字n(n $\ge k)$,都存在数组和为n的回文数组，且这个数组的和的长度刚好为k

思路

对于一个回文数组，如果是k是偶数的情况，那么他的回文数组和一定是偶数，那么当n是奇数的时候就不满足
反观k是奇数的情况，无论n是多少，我们可以让除了最中间的一个元素之外的所有元素都为1，中间的元素大小为n-k+1,一定满足条件

//Author: zengyz
//2025-07-17 13:53#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{int n;cin>>n;if(n%2==0)cout<<"NO"<<endl;else cout<<"YES"<<endl;return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while(_T --) {solve();}return 0;
}

B. Expensive Number

题目大意

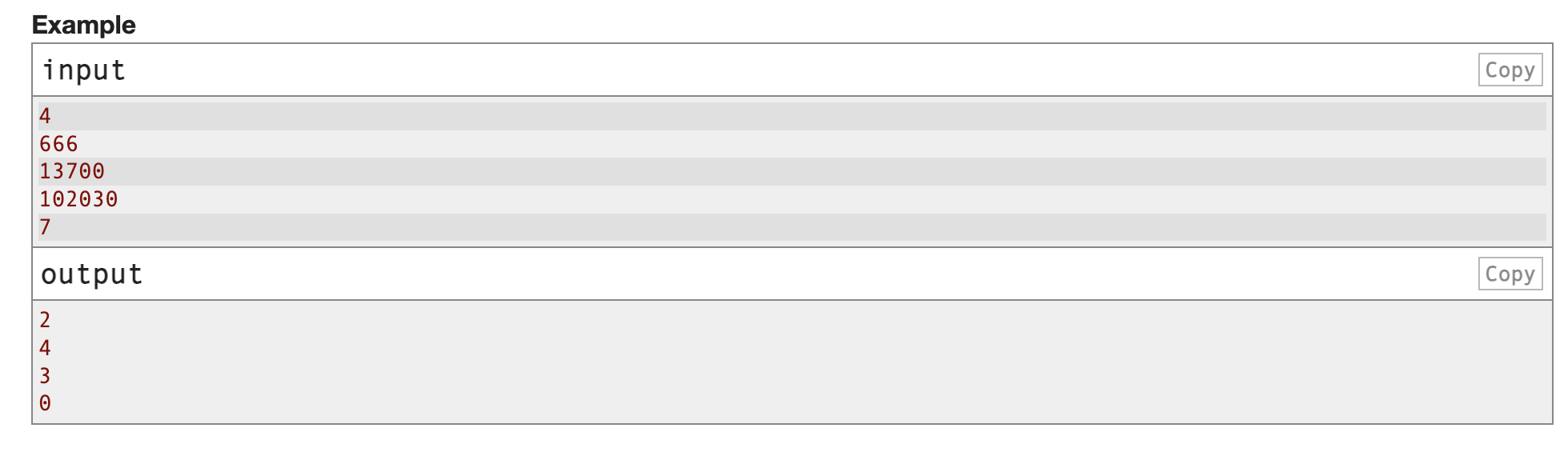
给你一个数字，定义它的代价为这个数除它每个十进制位上的数加起来
问最少去掉多少个数能够使得代价最小

思路

最小的代价一定是剩下一位，那么1/1=1
题目说删除出现的前导0可忽略，那么我们从前往后标记最后一位 非零位，删去之前所有的非零位，删除之后所有的0，就是答案

// Author: zengyz
// 2025-07-17 13:55#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{string s;cin >> s;int idx = -1;for (int i = 0; i < s.size(); i++){if (s[i] != '0')idx = i;}int cnt2 = 0;for (int i = 0; i < idx; i++){if (s[i] != '0')cnt2++;}for (int i = idx + 1; i < s.size(); i++){if (s[i] == '0')cnt2++;}cout << cnt2 << endl;return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}

C. Simple Repetition

题目大意

给你x,k,y等于x重复k次
问y是否为素数

思路

如果一个数为素数且k=1那么他还是素数，当k大于1时，y会存在x这个公因数导致变为合数
需要额外考虑11,即x=1,k=2的情况

// Author: zengyz
// 2025-07-17 14:00#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{int x, k;cin >> x >> k;if (x == 1){if (k == 2)cout << "YES" << endl;elsecout << "NO" << endl;return;}if (k != 1){cout << "NO" << endl;}else{for (int i = 2; i * i <= x; i++){if (x % i == 0){cout << "NO" << endl;return;}}cout << "YES" << endl;}return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}

D. Skibidi Table

题目大意

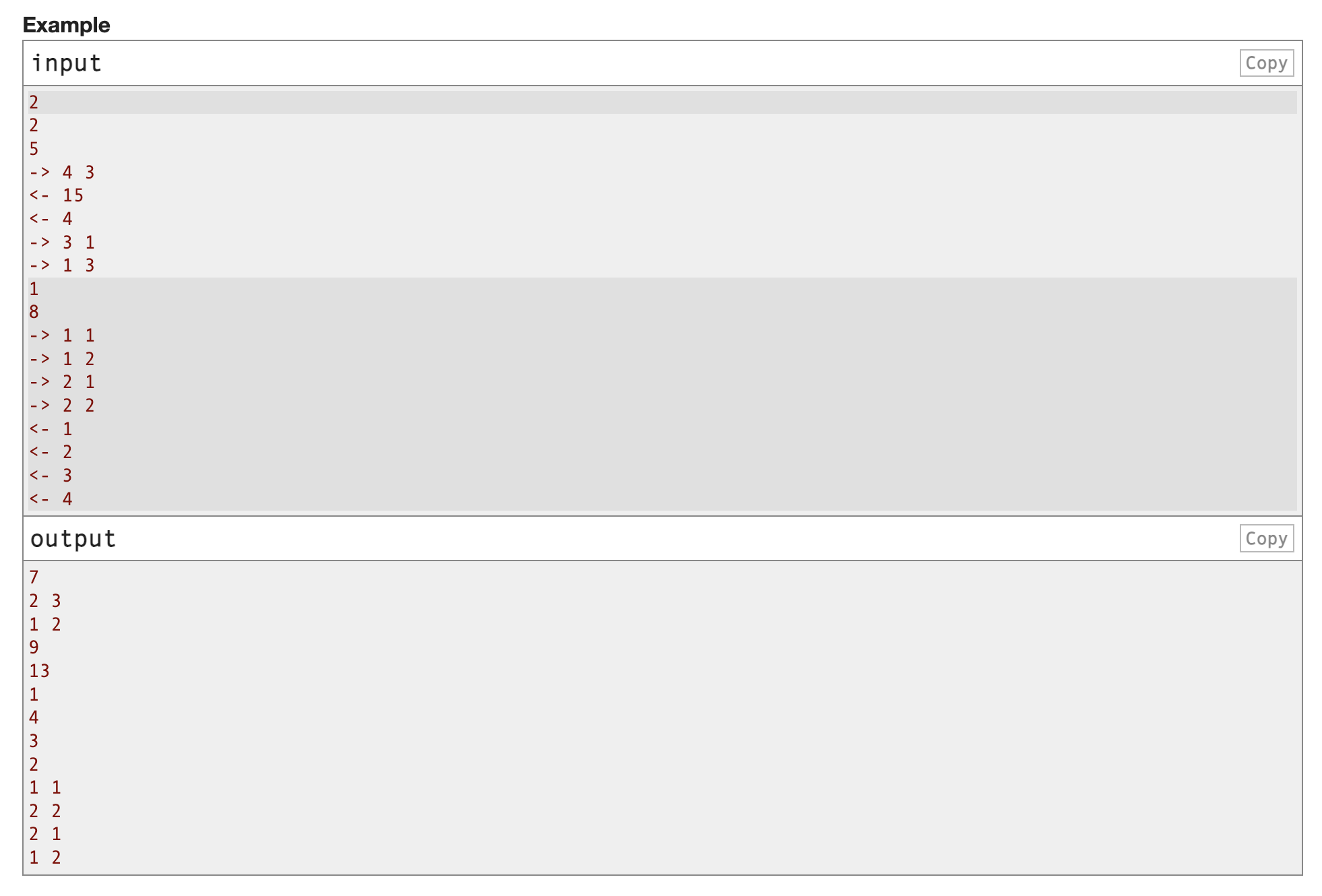
给你一个$2^n\ast 2^n$的矩阵，它会从2*2的小矩阵开始填，依次填左上、右下、左下、右上四个部分
，题目会询问q次，要么给你一个数问你它的位置，要么给你一个位置问它是多大

思路

不断递归
对于寻找一个位置(x,y)的值：
对于$2^n\ast 2^n$的矩阵来说
它的分界线是$2^{n-1}$,根据这个值判断是在四个部分中的哪一个
然后对(x,y)来说，将其模上分界线的长度$2^{n-1}$进入下一个小矩阵继续判断
每递归一次
总大小变为原来的四分之一
分界线变为原来的二分之一

对于寻找一个值的位置，我们反过来递归
定义minx,miny,maxx,maxy为可能的取值范围
这里我们计算分界线midx,midy
对于$2^n\ast 2^n$的矩阵来说
每一个小矩阵的大小为$2^{n-1}\ast 2^{n-1}$
用x/一个小矩阵的大小，看它是在哪一块
并不断缩小minx,miny,maxx,maxy
同时x需要模上小矩阵的大小$2^{n-1}\ast 2^{n-1}$以便递归进入小矩阵

每递归一次
总大小变为原来的四分之一

// Author: zengyz
// 2025-07-17 14:12#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{int n;cin >> n;int q;cin >> q;while (q--){string s;cin >> s;if (s[1] == '>'){ll x, y;cin >> x >> y;ll ans = 1;ll res = pow(2, 2 * n);ll tmp = pow(2, n);while (res && tmp >= 2){tmp /= 2;res /= 4;// cout << x << " " << y << " " << tmp << endl;if (x > tmp && y > tmp)ans += res;else if (x > tmp && y <= tmp)ans += res * 2;else if (x <= tmp && y > tmp)ans += res * 3;x = (x - 1) % tmp + 1;y = (y - 1) % tmp + 1;}cout << ans << endl;}else{ll x;cin >> x;x--;ll minx = 1, miny = 1, maxx = pow(2, n), maxy = pow(2, n);ll res = pow(2, 2 * n);while (x && res >= 4){res /= 4;ll midx = (minx + maxx) / 2;ll midy = (miny + maxy) / 2;int mod = x / res;x %= res;// cout << mod << endl;if (mod == 0){maxx = midx;maxy = midy;}else if (mod == 1){minx = midx + 1;miny = midy + 1;}else if (mod == 2){minx = midx + 1;maxy = midy;}else{maxx = midx;miny = midy + 1;}// cout << minx << " " << maxx << " " << miny << " " << maxy << endl;}cout << minx << " " << miny << endl;}}return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}

E. Min Max MEX

题目大意

给你n,k,让你将长度为n的数组分割成k个不同的数组，问这k个数组之中最小mex的最大值是多少

思路

二分mex，然后计算这样的情况是否合理
不能用set或map,容易超时，用unordered_map和unordered_set

// Author: zengyz
// 2025-07-17 15:33#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{int n, k;cin >> n >> k;vector<int> a(n);int maxx = -1;for (int i = 0; i < n; i++){cin >> a[i];maxx = max(maxx, a[i]);}maxx++;auto check = [&](int now) -> bool{int cnt = 0;int count = 0;unordered_set<int> st;for (int i = 0; i < n; i++){if (a[i] < now && !st.count(a[i])){count++;st.insert(a[i]);}if (count == now){cnt++;count = 0;st.clear();}if (cnt >= k)return true;}return false;};int l = 0, r = maxx;while (l < r){int mid = (l + r + 1) / 2;if (check(mid))l = mid;elser = mid - 1;// cout << l << " " << r << endl;}cout << l << endl;return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}

F. Hackers and Neural Networks

题目大意

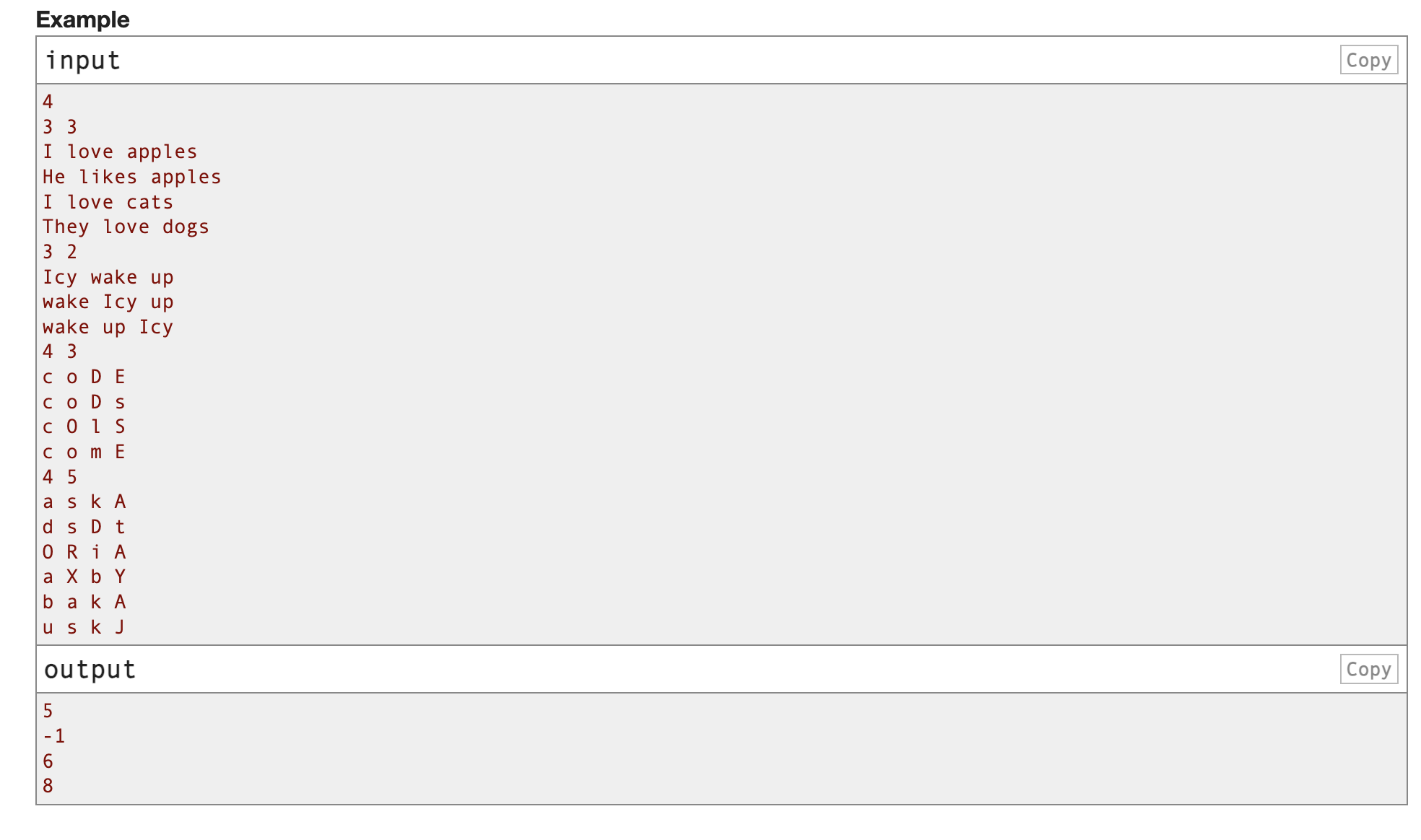
给你n,m
n为需要的目标串a的长度
然后会给你m个长度为n的串

给你一个空白串c，你可以进行如下操作：
选择m中的一个串，它会选择串c中任意一个空白位置，并将对应自己位置的元素赋值上去
删除c串中任意一个非空位置上的元素，让它变成空白位置

问你最多进行多少次操作，可以让c串变为a串

思路

首先我们记录一下对于串a上的每个元素，是否都存在m个串中相同位置有匹配的情况，只要在1~n上有一个位置在m中找不到相同位置有匹配，那么就肯定构造不出来

然后我们记录一下m个串在相同位置和a匹配的最多元素个数maxx
那么我们就让这个串操作m次，将c填满变成这个串的样子，然后删一个不符合的位置，再找m中匹配这个位置的一个串操作，由于只有这个位置是空白的，它一定会赋值这个匹配的值，这样的总操作次数是n+2*(n-maxx)次

// Author: zengyz
// 2025-07-17 15:54#include <bits/stdc++.h>using namespace std;
typedef long long ll;void solve()
{int n, m;cin >> n >> m;vector<string> a(n);vector<vector<string>> b(m, vector<string>(n));for (int i = 0; i < n; i++)cin >> a[i];vector<int> idx(m);map<int, int> mp;int maxx=0;for (int i = 0; i < m; i++){int count = 0;for (int j = 0; j < n; j++){cin >> b[i][j];bool flag = true;if (b[i][j] == a[j]){count++;mp[j] = 1;}}maxx=max(maxx,count);}for (int i = 0; i < n; i++){if (mp[i] == 0){cout << -1 << endl;return;}}ll ans = n + 2 * (n - maxx);cout << ans << endl;return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int _T = 1;cin >> _T;while (_T--){solve();}return 0;
}