当前位置：首页 > news >正文

热点综述│高效泛化求解新范式：神经算子综述

news 2025/7/17 9:49:12

近年来，得益于计算硬件的突破性发展，深度学习技术已在多个学科领域得到了广泛应用。相关研究表明，深度神经网络在解决数学问题特别是偏微分方程的求解方面表现出了巨大的潜力，神经算子以其卓越的计算效率与出色的泛化性能，成为了传统数值求解器的有效替代，构造了科学计算新范式。中南大学刘圣军老师SGICL课题组与西安交大的孟德宇老师合作，在《Neurocomputing》期刊上就神经算子的发展与前景问题发表了综述论文《Architectures, variants, and performance of neural operators: A comparative review》。该文章梳理了近两百篇文献，对神经算子的各个变体和扩展进行了归纳与讨论，并通过数值实验对其特性进行了全面的分析与总结。基于这些讨论与分析，该文针对不同神经算子所面临的挑战和潜在改进提出了展望与建议，为神经算子的实际应用和未来发展提供了有价值的指导。该论文的基本信息见图1。

图1 论文基本信息

文章引用：Shengjun Liu, YuYu, Ting Zhang, Hanchao Liu, Xinru Liu, Deyu Meng. Architectures, Variants, and Performance of Neural Operators: A Comparative Review [J]. Neurocomputing, 2025: 130518. https://doi.org/10.1016/j.neucom.2025.130518.

论文链接：https://authors.elsevier.com/a/1lGG23INukW7x3

代码链接：https://github.com/YuYu8900/Neural-Operators

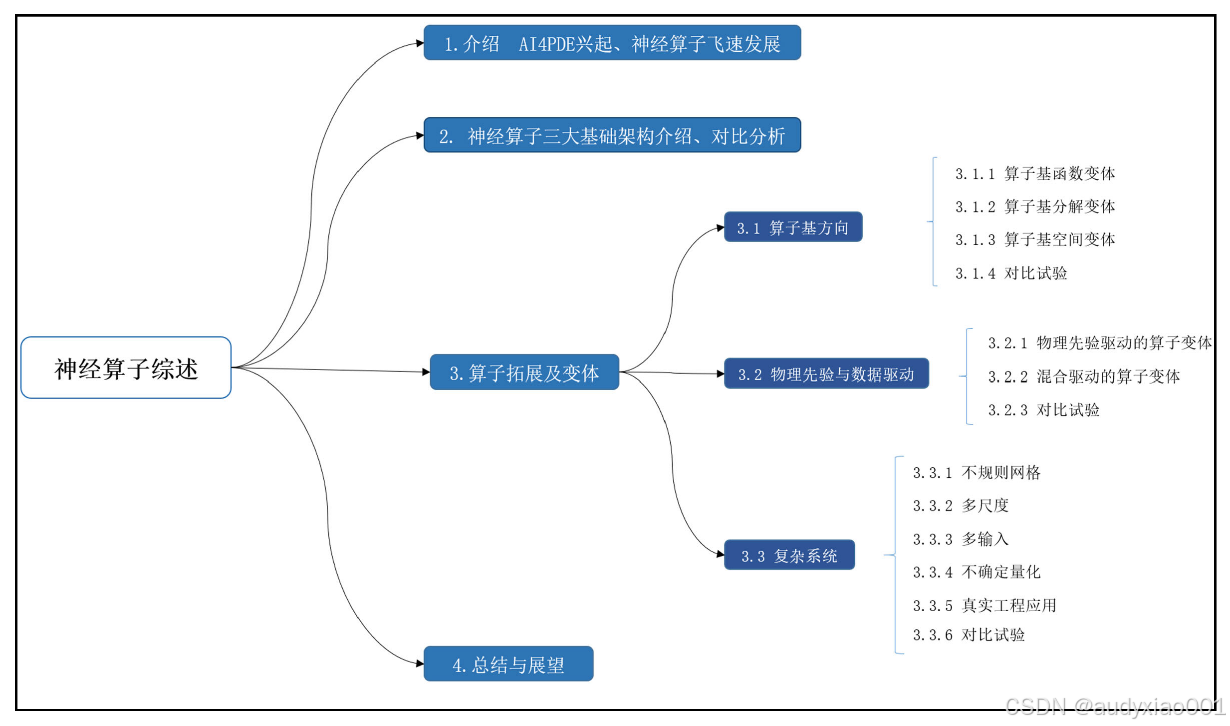
图2 论文的组织架构

近年来，神经算子（Neural Operators）逐渐成为传统数值求解方法的有力替代方案，凭借其高效的计算能力、出色的泛化性能和优秀的求解精度，受到了广泛关注。论文围绕神经算子的研究进展进行了系统综述与深入分析，论文的组织架构如图2所示。根据网络结构的不同，可以将神经算子划分为三大类：

1. 深度算子网络（Deep Operator Networks, DeepONets）

2. 积分核类神经算子（如图神经算子GNO、傅里叶神经算子FNO）

3. 基于Transformer的神经算子（如Galerkin Transformer、通用神经算子Transformer GNOT）

在此基础上，文章进一步从以下三个方向出发，对各类神经算子的变体与扩展方法进行了梳理与归纳：

a) 基于算子基的神经算子变体；

b) 融合物理先验的神经算子拓展；

c) 面向复杂系统建模的神经算子应用。

此外，文章还通过数值实验对不同算子方法的特性与性能进行了对比分析。在综述与分析的基础上，文章最后针对当前神经算子在理论、方法和应用中的挑战与不足，提出了未来的研究方向与改进建议，力求为神经算子的实际应用与持续发展提供系统性、可操作的参考。

本推文作者为刘汉超、余煜，审核为刘圣军、孟德宇。本推文由论文的原作者撰写并发布，为原创文章，所有材料具有原始版权。

一、神经算子的重要性

偏微分方程（PDE）在物理、化学、生物和工程等多个领域中扮演着至关重要的角色，被广泛用于复杂自然过程的模拟。用于求解PDE的传统数值方法（如有限差分法和有限元法）高度依赖求解域的网格离散，尤其在处理高维PDE时，需要大量的网格节点，导致计算成本极高。同时，一旦方程的各种初始边界条件和相关参数发生变化，这些传统方法往往需要重新计算，缺乏灵活性，严重限制了其实用性。

近年来，随着神经网络技术的发展，其强大的函数逼近能力引起了研究者的关注。相比传统方法，神经网络具备学习能力和自适应性，能够高效逼近高度非线性的函数，因此被视为一种有前景的PDE求解替代方案。其中，一种较早受到关注的方法是物理信息神经网络（Physics-Informed Neural Networks, PINNs）。这类方法通过将已知的物理规律融入神经网络结构和损失函数，使模型能够在部分未知或高度不确定的场景中进行数据与物理模型的融合，成功应用于高维PDE的求解问题，突破了“维度灾难”的限制。然而，PINNs仍存在局限：它们通常只能解决一个特定的PDE问题，一旦方程参数发生变化，就需要重新训练网络；同时，对于一些自然过程，物理规律本身可能并不明确或过于复杂难以融入神经网络的结构和损失函数，这进一步限制了PINNs的适用性；而且，在低维问题中，PINNs的计算速度和精度往往不如传统方法。

为突破这些限制，深度算子网络（DeepONet）被提出，由此开启了“神经算子”这一新方向。神经算子可以学习函数空间到函数空间的映射关系，从而实现“一次训练，解决一类PDE”的目标。这意味着，在处理具有多个参数或不同边界条件的PDE类时，只需进行一次的模型训练即可泛化到一类的PDE的求解。更重要的是，神经算子能够适配复杂的边界条件和不规则几何结构，具备更强的通用性。

目前，多种不同的神经算子架构被提出，包括DeepONet、积分核型神经算子，以及基于Transformer的神经算子等。这些方法在高效求解复杂系统中的PDE方面具有出色的表现，并已在多个实际应用中取得了不错的结果。当然，神经算子也存在挑战，例如，在处理复杂问题时往往需要大量的训练数据，这成为其大规模推广的主要障碍。但尽管如此，神经算子凭借其强泛化能力和在复杂问题建模中的潜力，依然是当前科研领域的研究热点，相关研究不断涌现。更值得一提的是，神经算子本质上是函数空间之间的映射模型，因此在PDE求解之外，在其他科学领域也展现出极大的应用前景。例如：在自然灾害模拟中，研究者提出了一种基于神经算子的扩散模型采样方法，用于加速森林火灾等复杂系统的模拟；在生成模型方向，有研究提出通过神经算子实现概率分布到其得分函数之间的映射，具备对未见分布的泛化能力；在计算机视觉领域，神经算子也被用于任意尺度的图像超分辨重建和移动设备上的轻量部署；此外，在神经常微分方程、图像生成、时间序列建模、隐式神经表示等多个前沿领域，均可见其身影。

目前已有的关于神经算子的综述文章大多只关注某一类的算子架构（例如只关注积分核算子的分析与讨论），或仅对DeepONet和FNO进行对比分析，缺乏对神经算子整体框架的全面而系统的梳理和评估。因此，论文尝试从底层架构演进的角度出发，系统总结神经算子的研究进展，挖掘不同架构之间的共性与差异，梳理关键发展路径。论文重点关注以下几个方面：

(1) 首先介绍神经算子的代表性架构，包括DeepONet、积分核型神经算子以及基于Transformer的神经算子，并分析其各自的优势与局限；

(2) 其次，从三个方向出发，探讨神经算子在架构上的多样化演化路径，包括基于算子基的变体、融合物理先验的变体、以及面向复杂系统建模的应用；

(3) 最后，总结神经算子的演化趋势、当前挑战与未来潜力，为该领域的持续研究和实际应用提供参考。

二、神经算子的定义及分类

2.1 神经算子的定义

神经算子（Neural Operator）是一类用于学习函数到函数映射（function-to-function mapping）的深度学习模型，适用于偏微分方程（PDE）求解、物理建模、科学计算等问题。与传统神经网络关注“输入到输出”之间的数值映射不同，神经算子的目标是直接近似一个用于描述函数空间之间映射的算子——即输入为函数，输出仍然是函数。各种类型的神经算子均以端到端的形式学习逼近输入函数到输出函数两个函数空间之间的映射关系。如图3所示，以达西方程为例，神经算子可以直接学习参数函数到解函数的映射，在训练完成后，给定任意的参数条件，神经算子都可以直接预测对应的解函数。

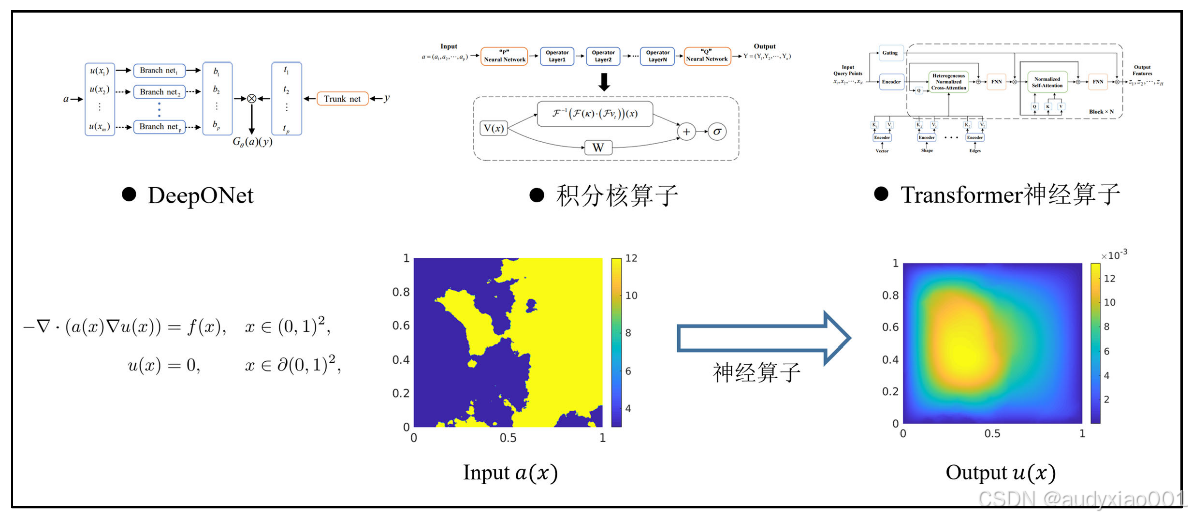
图3 神经算子示例

2.2 神经算子的发展历程

如图4所示，自从2019年DeepONet出现以来，神经算子方法飞速发展，涌现出了大量成果。与PINNs方法的思路类似，受神经网络的算子通用逼近定理启发，Lu等人设计了DeepONet网络架构，从数据集中学习无限维函数空间之间的映射。后续Li等人引入了一种称为积分核算子的通用架构，通过对算子层的积分核进行不同的设计，GNO、FNO等方法被提出。在这两类算子基础上，DeepONet类方法通过引入多尺度分支、物理信息融合（如PDE残差约束）等手段，显著提升了对不同任务和几何形状的适应能力；积分核算子类方法则依靠可学习的图卷积核、频域全局卷积（FNO及其变种）以及低秩或稀疏核分解，在保持高精度的同时大幅降低了计算和存储开销；而在Transformer神经算子方面，Cao 等人在GK‑Transformer中率先将自注意力机制引入算子学习，用来捕捉非结构化网格上的全局依赖；其后各种关于Transformer架构的神经算子方法相继问世，它们通过注意力机制对几何、边界条件与场量等多源输入进行全局建模，进一步提升了对复杂非线性耦合和跨尺度依赖的表征能力，为工程级CFD和多物理场仿真中的高效、可扩展神经算子落地打下了坚实基础。

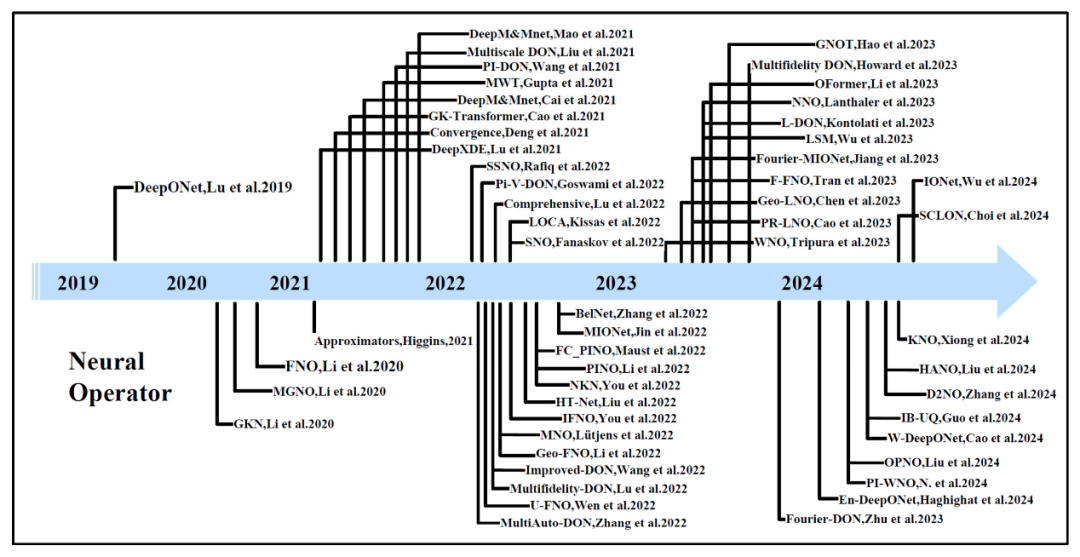
图4 神经算子发展历程

2.3 神经算子三大基础架构分类

根据模型结构，神经算子可分为三类主流架构：（1）基于通用逼近定理的DeepONet；（2）基于网格或图结构的积分核型神经算子；（3）基于Transformer的神经算子。目前，大多数新提出的神经算子模型基本上都是在这三类架构的基础上进行的修改或扩展。下面是对三类神经算子基础架构的详细介绍。

2.3.1 DeepONet神经算子

Lu等人提出的DeepONet，是提出最早，也是最基础的一类神经算子，其基本思想是基于通用的函数逼近定理，用神经网络来学习算子映射。换句话说，它学习的是一个“函数到函数”的映射过程：输入是可以控制PDE变化的函数（如源项、边界条件等），输出则是PDE的解函数。DeepONet的结构如图5所示，主要由两部分组成：Branch网络：负责接收初始/边界函数、源项等函数信息；Trunk网络：负责接收空间坐标等“查询点”作为输入。这种设计非常灵活，可以根据不同任务选择不同的网络结构。例如，Branch和Trunk网络可以是普通前馈神经网络（FNN），也可以是卷积网络（CNN）等。

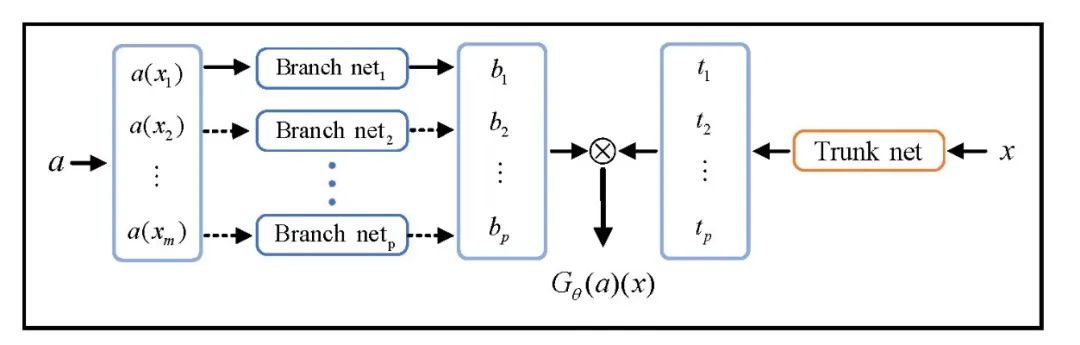
图5 DeepONet架构

DeepONet的优势：

1) 通用性强：基于神经网络强大的逼近能力，DeepONet能够学习复杂的非线性映射。

2) 不依赖网格：与传统数值方法不同，它不需要事先构建网格，因此适用于不规则几何或复杂边界条件。

3) 解决算子问题：一次训练可适配一整类PDE方程，而非单个实例。

DeepONet的局限性：尽管结构简洁，能力强大，DeepONet仍然存在一些实际挑战：

1) 对训练数据依赖大：作为数据驱动方法，效果高度依赖数据质量和样本数量。

2) 离散化误差问题：Branch网络的输入需要在有限维度空间内进行离散表示（也就是“传感器点”）。在处理高维或复杂问题时，这种离散化可能会带来性能下降。

3) 结构和超参数选择困难：网络结构和参数的选择对结果影响较大，缺乏统一的设计准则。

2.3.2 积分核型神经算子（Integral Kernel Operator）

Li等人最早提出了图神经算子（Graph Neural Operator，GNO），将图神经网络与Nyström近似理论结合应用于算子学习。随后，他们又引入了一种更通用的结构——积分核型神经算子（Integral Kernel Operator）。该类架构的研究重点是：如何在神经网络的线性算子层中设计积分核，从而提升模型的表达能力。积分核神经算子通过组合线性积分算子与逐点非线性激活函数，从而逼近复杂的非线性映射。这种结构本质上是定义在函数空间上的“深层网络”，输入和输出都是函数，不依赖特定的离散化方式。其中，典型的代表性模型为傅里叶神经算子（Fourier Neural Operator、FNO）。

FNO是目前最成功、应用最广泛的神经算子之一。如图6所示，它的核心思想是：将积分操作通过傅里叶变换在频域中实现，利用快速傅里叶变换（Fast Fourier Transformation，FFT）进行高效计算，从而提高计算速度和准确率。

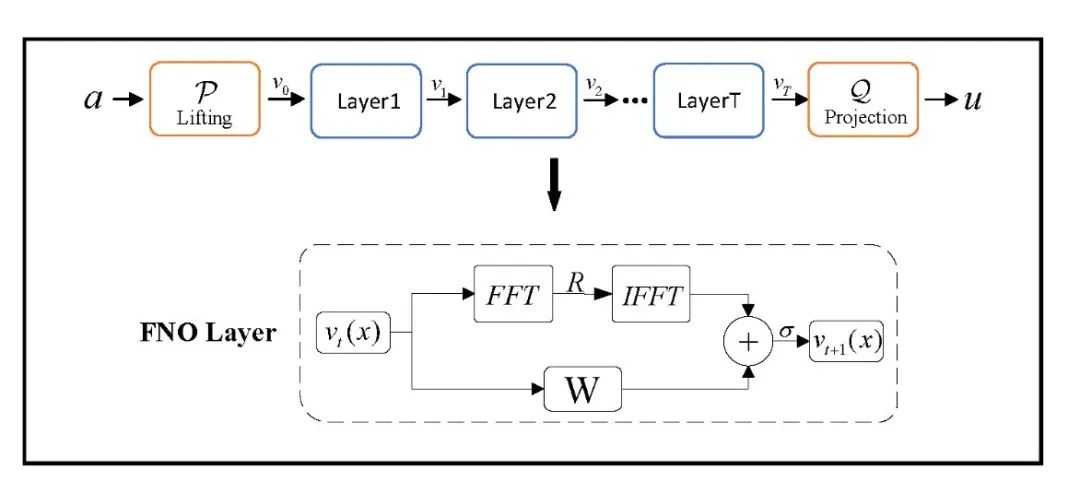
图6 傅里叶神经算子

其优势包括：

a) 快速计算：FNO基于FFT，具有准线性时间复杂度；

b) 精度高：频域处理可以提取函数的全局特征；

c) 广泛适用：FNO已在气候预测、湍流建模、超分辨率等多个方向中成功应用。

不过，FNO的一个限制是：它依赖于规则网格（uniform grid），因此不能直接处理非结构化数据。同样的，它也受限于维度灾难（curse of dimensionality）。

总体来说，积分核型神经算子架构相比于DeepONet更加强大和灵活，其核心优势是：

a) 具备建模非局部依赖关系的能力；

b) 在函数空间中直接建模，无需特定网格；

c) 可通过不同参数化方式适应不同任务，如图结构（GNO）、频域（FNO）分别处理不规则和规则数据等。

这类神经算子也为后续更多样化的架构（如基于Transformer的神经算子）提供了框架基础。

2.3.3 Transformer神经算子

注意力机制自2014年由Bahdanau等人首次提出以来，已在自然语言处理等多个领域获得了广泛应用。它通过从“全局聚合”转变为“重点关注”，极大地提升了模型的表达能力和泛化能力，成为许多机器学习任务中不可或缺的工具。

Cao等人在2021年首次将线性Transformer引入算子学习中，提出了GK-Transformer (Galerkin Transformer) 模型。他们发现，缩放点积注意力与傅里叶类核积分变换在数学形式上有着惊人的相似性，因此提出注意力机制可以看作是一种可学习的积分算子。与此同时，Kovachki等人也从理论角度证明了注意力机制其实是神经算子层的一种特殊形式。然而，GK-Transformer也存在一定的局限性：它要求输入和输出必须在相同的网格（mesh）上进行表示。这种限制在处理多输入、多尺度或不规则网格的问题时，显得不够灵活。

为了解决这一问题，研究者进一步提出了更具通用性的GNOT（General Neural Operator Transformer）架构。如图7所示，GNOT支持任意位置的输入和输出，可处理多个输入函数、不规则网格以及多尺度问题，极大地拓展了神经算子的应用范围。该模型通过交叉注意力、自注意力与门控前馈网络的组合，使得每一步更新都能兼顾输入函数的全局信息与查询点的局部特征，从而实现高效且灵活的算子学习。

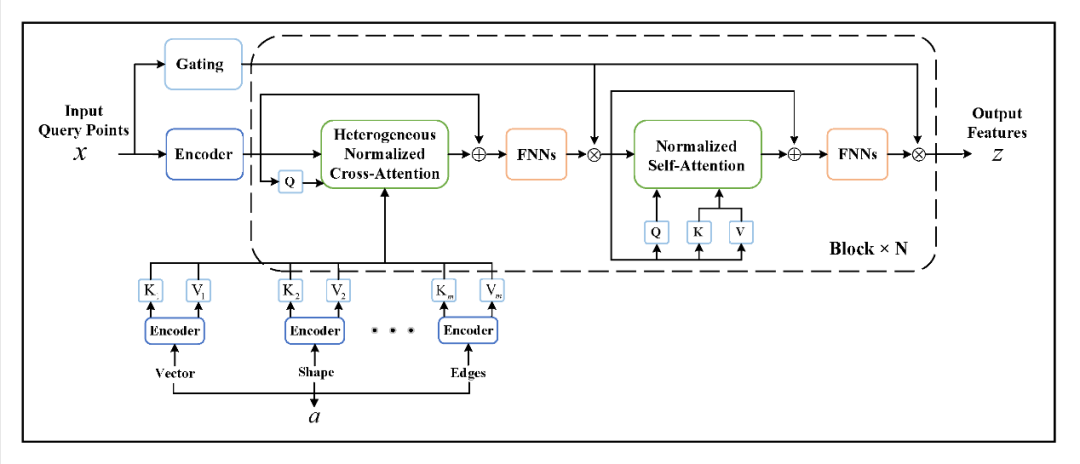
图7 GNOT的网络架构

在实际应用中，Transformer神经算子展现出极强的表达能力，不仅适用于物理建模领域，如流体力学、电磁场模拟等，还可以广泛应用于图像处理、医学重建等其他类型的算子学习任务。与最初用于求解偏微分方程（PDEs）的积分核算子和DeepONet不同，Transformer最初应用于自然语言处理（Natural Language Processing , NLP）任务，后因其高效特征捕捉能力被引入算子学习。尽管Transformer在求解简单PDE时不显著优于其他算子，但在复杂高维PDE问题中能提供更高准确度。它特别擅长处理大规模数据集，通过更大的模型容量来减少误差。然而，Transformer算子需要更多的时间和参数，相较其他方法其计算开销较大。

三、神经算子拓展及变体

基于三类神经算子的主流架构，研究者们从网络结构和应用场景两方面出发，先后提出了多种算子变体。为便于梳理其发展脉络并洞见未来趋势，论文从三个角度对算子变体进行了归纳总结，包括基于算子基的变体、融合物理先验的变体、以及面向复杂系统建模的应用。

3.1 基于算子基的变体

基于算子基的神经算子变体主要利用不同的函数基底、扩展基空间或分解技术来增强原有架构的稳定性、灵活性和表达能力。

3.1.1 基于不同基函数的变体

受傅里叶神经算子将傅里叶变换引入积分核算子架构中，在频域学习逼近算子映射的启发，众多研究者从基函数出发，拓展设计了新的算子模型。

小波神经算子（Wavelet Neural Operator , WNO）用时频双域的小波基替代FNO的全局傅里叶基，不仅保留了多尺度分析能力，还能在非规则网格和突变信号场景中保持鲁棒性。WNO在处理不连续或尖峰特征时，比传统傅里叶方法具有更好的局部捕捉能力。类似的，在DeepONet中引入小波变换催生了W-DeepONet (Wavelet DeepONet)，它分别对信号的小波近似系数和细节系数采用两组分支／主干网络进行学习，从而同时捕获系统的瞬态响应和稳态趋势，显著提升了算子对时间动态的建模精度。拉普拉斯神经算子（Laplace Neural Operator, LNO）用拉普拉斯变换代替傅里叶变换，并通过留数分解形式将瞬态（极点）和稳态（频率）响应分离建模。而同样结构设计的PR-LNO (Pole-residue Laplace Neural Operator) 能有效处理非周期信号、复杂几何以及不稳定系统，是对FNO在瞬态建模局限的有力补充。谱神经算子（Spectral Neural Operator, SNO）及其改进版OPNO(Orthogonal Polynomial Neural Operator)、SCLON(Spectral Coefficient Learning via Operator Network)以三角多项式、Chebyshev或Legendre多项式为基，对函数进行有限级的谱展开，让网络只需学习系数映射。SNO能实现高精度无损插值，但对光滑数据有依赖；OPNO引入了自动满足边界条件的紧致组合基；SCLON使用线性组合的Legendre基，在保证高效率的同时兼顾了谱方法的准确性。

3.1.2 基于算子基分解的扩展

分解式扩展方法通过对主算子进行维度或模态分解进一步优化其性能。F-FNO（Factorized Fourier Neural Operator）对每个空间维度进行独立傅里叶处理，大幅降低复杂度、提高深度网络稳定性；PODDeepONet先用POD(Proper Orthogonal Decomposition) 提取数据主模态，再让DeepONet学习这些基函数的系数，既实现了降维又强化了特征表达；SSNO (Spatio-Spectral Neural Operator) 在Fourier卷积层中注入输入混合器和低通滤波器，保证信息完整传递，进而提升精度；Koopman神经算子（Koopman neural operator , KNO）结合Hankel矩阵与Koopman不变子空间理论，通过延迟嵌入和频率分解有效预测高维PDE的长期动态。

这些基于不同算子基和分解策略的变体，极大地扩展了神经算子的适用范围，从非规则网格、非平稳信号到复杂几何、多模态系统，都能够获得更稳健、更高效的求解效果。

3.1.3 基于基函数空间的扩展

在基函数空间扩展方向上，研究者通过引入高维编码、潜在空间和新型算子结构来提升算子的表达能力。Improved‑DeepONet在分支和主干之间加入两个编码器，将输入映射到高维特征空间，并在网络各层通过点对点融合增强非线性表达；Latent Spectral Model（LSM）借助注意力机制将高维数据映射到低维潜在空间，并用三角＋正余弦基对潜在坐标编码，有效去除冗余、捕捉内在物理信息；L‑DeepONet则在DeepONet中嵌入无监督自编码器，在潜在空间中学习算子映射，显著提升时变PDE的预测精度和效率，但不适合空间外推；En‑DeepONet增加了加、减运算分支，除了原有的乘法，还对主干和分支输出做“相加”“相减”组合，从而能学习更广泛的算子尤其是移动解算子；NOMAD (Nonlinear Manifold Decoders) 用一个专门的非线性解码器来联合分支输出与坐标基特征，对数据的低维流形进行更贴合的非线性降维和重构；Waveformer则将小波多分辨率特征与Transformer长程依赖建模结合，既能捕捉复杂的空间振荡特征，又能有效模拟长期时序演化。

3.1.4 算子基实验

论文比较了不同基函数扩展的神经算子在多个PDE数据集上的表现，这些数据集在维度、连续性和规则性上各不相同，具体有关方程数据集的细节可以参照表1。所有实验均在单张RTX 4090 GPU上进行，参数设置见论文附录。论文采用相对误差来评估不同算子在各类问题上的精度和稳定性。

表1 算子基实验方程

表2 算子基实验对比结果

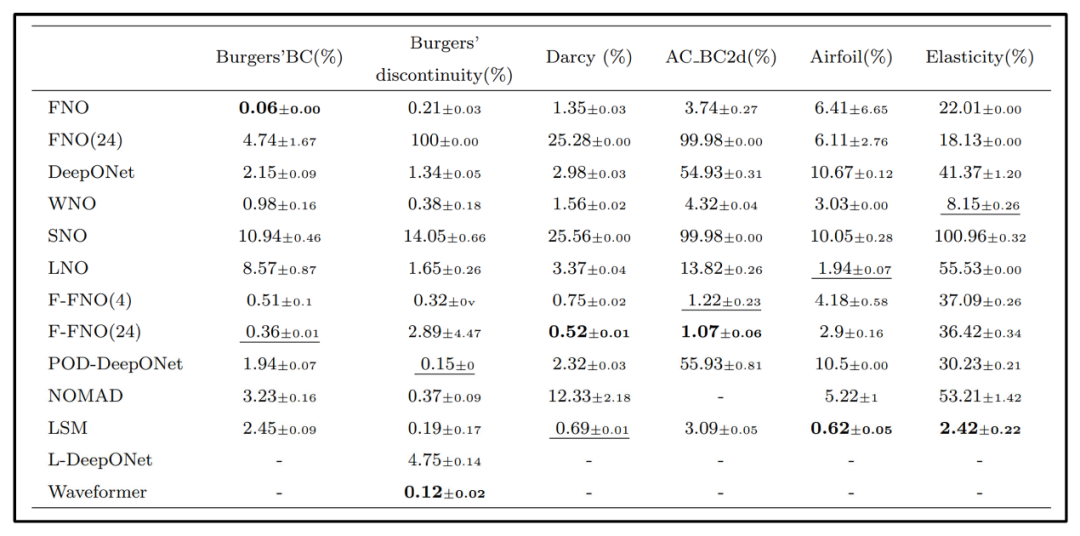
有关算子基各种变体的对比实验如表2所示。针对基分解的拓展，从稳定性测试来看，当网络深度从4层增至24层时，FNO在大多数基准上表现不稳定，尤其在非光滑问题（如对流方程、有间断的Burgers方程和Allen‑Cahn方程）上几乎无法收敛；而F‑FNO由于引入了傅里叶分解和改进的残差连接，减少了模型复杂度，能够稳定扩展到深度网络，并在这些问题上取得了最优或接近最优的结果。针对基函数的变种，WNO优秀地捕捉了空间局部特征，在大多数数据集上都能获得极高的精度，且在不规则网格数据上的表现优于FNO。由于Gibbs现象的限制，SNO仅适用于输入输出都很光滑的问题，对复杂或不连续场景无法很好地建模。LNO针对某些特定类型PDE（如带有瞬态成分或非周期信号）进行了优化，对Darcy流问题表现一般，但在处理带有间断特征的Burgers方程时效果显著。引入注意力机制的LSM在大多数基准上表现出最佳或接近最佳的性能，并通过三角基解决了FNO对规则网格的依赖。相比之下，原始DeepONet在带有明显瞬态响应的问题（如Allen‑Cahn）上效果较差；POD‑DeepONet利用先验的POD模式增强特征提取能力，在大部分基准上优于DeepONet。

总体来看，各算子的优势与所选基函数密切相关：WNO的局部小波基更善于处理间断与突变；F‑FNO、POD‑DeepONet等分解策略能够补充更多特征信息，提升稳健性和准确率；而注意力或潜在空间方法（LSM、Waveformer）则擅长从大规模高维数据中提取长程依赖和主要物理信息。基函数的选择与改进因此成为优化神经算子性能的关键切入点。

3.2 融合物理先验的神经算子

基于数据驱动的神经算子对数据质量的依赖度较高，需要大量高质量训练数据的支撑。实际问题中常见三种情形：一是物理信息完备但数据稀缺；二是数据与物理信息均部分可得；三是数据充裕但缺乏物理先验。其中第二种情况最为普遍，也催生了多种混合方法。如图8所示，通过将已知的物理信息（如方程、初始边界条件等）嵌入到损失中，将物理信息约束与数据驱动的神经算子相结合，可以缓解纯数据驱动方法对大量高质量训练数据的依赖。将神经算子的高效性与物理信息的可靠性结合，既能加速求解又能保证精度。

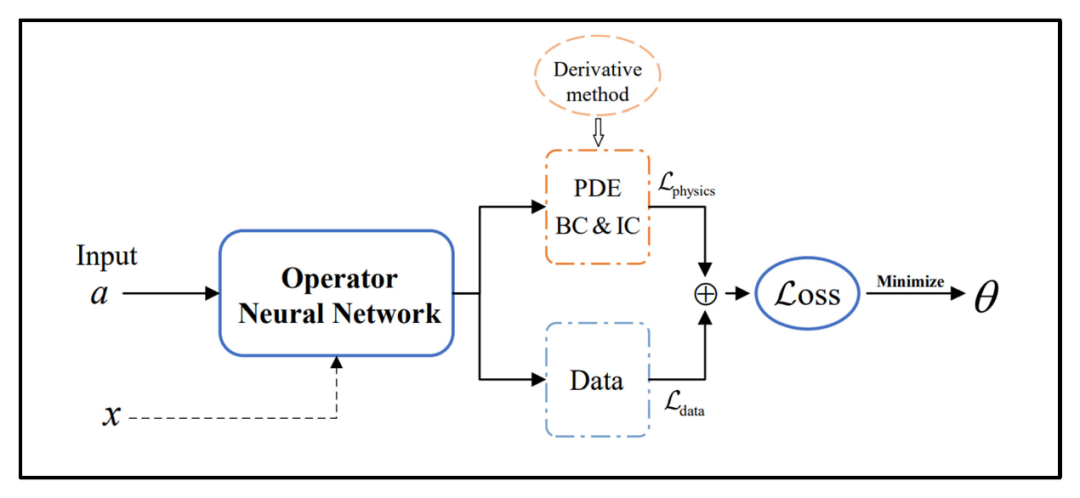
图8 融合物理先验的神经算子

3.2.1 物理信息驱动的神经算子

针对物理信息完备但数据稀缺的情况，一些纯物理信息驱动，无需训练数据的神经算子方法被提出。在DeepONet的基础上，物理信息神经算子（Physics-informed DeepONet PI‑DeepONet）将PDE作为约束项加入损失中进行训练，通过自动求导的方式计算网络输出对空间坐标的偏导，并在损失中同时考虑数据拟合和PDE残差。与纯数据驱动的版本相比，PI‑DeepONet在精度、收敛速度和泛化能力上均有明显提升。类似地，IONet (Physics-Informed Loss Interfaced Operator Network) 针对参数化椭圆型PDE，分别对不同的系数、源项和边界条件设定专门的分支并附加对应的物理损失，实现高精度求解。

在傅里叶神经算子框架下，PINO (Physics-Informed Neural Operator) 将粗分辨率数据与高分辨率PDE约束共同训练，不仅继承了FNO的离散不变性，还能在更高分辨率上准确预测。PINO在频域中利用傅里叶变换精确计算导数，但因Gibbs效应限制，需针对非周期问题引入改进的谱导数计算方法。基于WNO的PI‑WNO则通过随机投影梯度进一步提高了导数计算的准确性。

3.2.2 混合驱动的神经算子

针对数据与物理信息均部分可得的情况，一些混合驱动的神经算子方法被提出，物理信息和训练数据耦合作用，训练算子网络更加高效准确地逼近算子映射。

混合算子在多保真度学习中大显身手：高维问题的高保真数据成本高昂，可用低保真数据加物理约束进行校正，再辅以少量高保真样本，既可以节省计算资源，又获得了接近高保真水平的解。又如DeepM&Mnet可在新场景下用少量数据和物理损失对预训练算子进行微调，实现快速迁移并保持高精度；即使仅有部分变量观测，也能在物理先验约束下给出可靠预测。

此外，当需要对超出训练域的输入做外推时，纯数据驱动算子往往失效。物理信息神经算子可通过在预训练模型上加入PDE残差损失进行再训练，从而在外推情形下仍可保持合理准确的预测能力。总结来看，将物理信息融入神经算子，不仅提升了数据效率和模型稳定性，也扩展了算子在少样本、高保真、跨分辨率和外推问题中的应用潜力。

3.2.3 融合物理先验算子实验

为探讨物理先验对于神经算子结构的影响，论文选取了四个在维度和空间特性上各不相同的数据集，对比分析了FNO、WNO和DeepONet在三种训练方式下的表现：仅物理约束(w/o data)、仅数据驱动(only data)，以及物理＋数据混合式训练(with data)。在不同数据实例上，各算子的相对误差结果如表3所示。

表3 物理信息与数据驱动的神经算子对比试验结果

结果表明，仅依赖物理信息的FNO与WNO往往难以在Burgers方程等复杂边界的问题上得到准确求解。虽然PI‑WNO在Burgers方程上的纯物理训练效果不佳，但将物理约束与数据驱动相结合后其预测精度明显提升，在Burgers方程、扩散-反应方程及Allen‑Cahn方程上都可取得与纯数据训练同等或更好的结果。

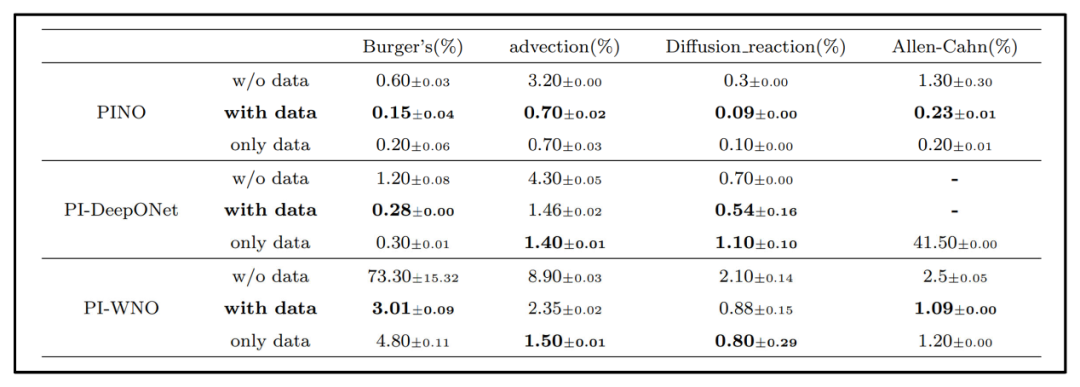
为了考察物理先验对模型在噪声干扰条件下的鲁棒性的影响，论文构造了加噪的训练和测试集来进行对比试验。噪声数据是在原始输入上叠加幅度为原函数最大值十分之一的高斯白噪声生成的。

表4 噪声鲁棒性实验结果

从表4中的实验结果可以看出，在Burgers方程数据上，向输入函数叠加10%振幅的高斯噪声后，纯物理或纯数据驱动下算子求解精度都有所下降，而混合模型在干净和有噪声数据上都能取得与纯数据驱动相当甚至更好的结果。

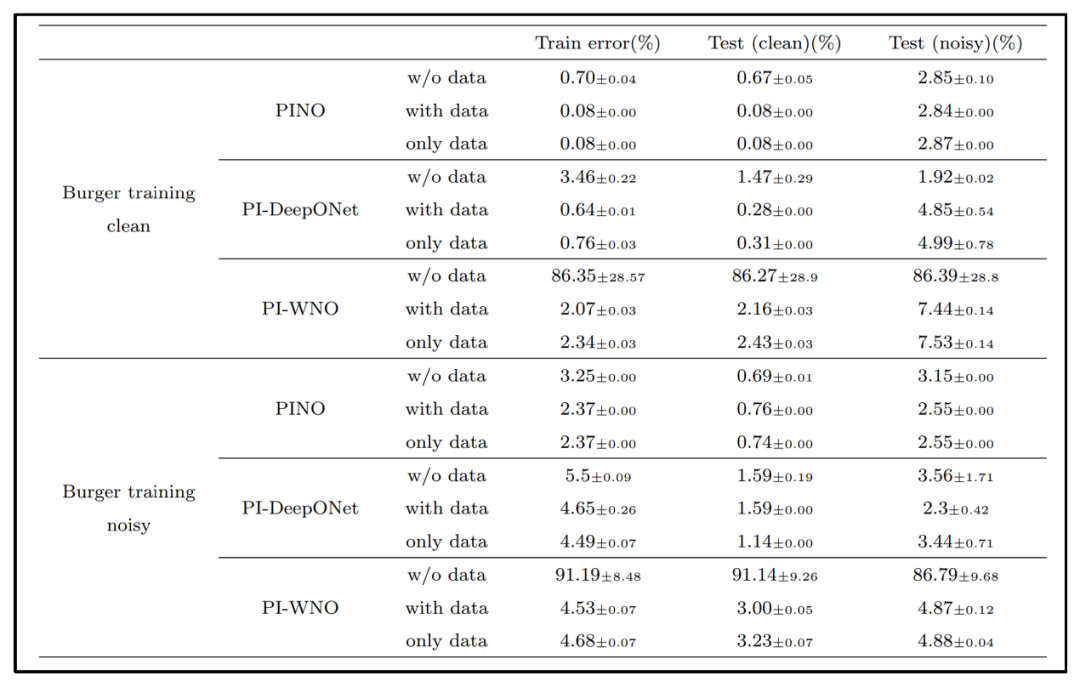
表5 跨分辨率实验结果

同样地，针对不同分辨率物理先验的影响论文也进行了相应的对比试验。在跨分辨率测试中，论文使用低分辨率数据训练PINO，并分别施加不同分辨率的PDE约束来评估其泛化能力。由于DeepONet缺乏离散不变性、WNO在调用小波包时对输入分辨率不具备自适应性，因此此部分实验仅对PINO进行。如表5所示，以PINO为例，仅用低分辨率训练数据和低分辨率PDE约束时，模型在高分辨率测试上的误差仍较大；加入高分辨率PDE约束后，误差显著下降，说明高精度PDE残差有助于算子在不同网格下保持性能。

表6 外推实验结果

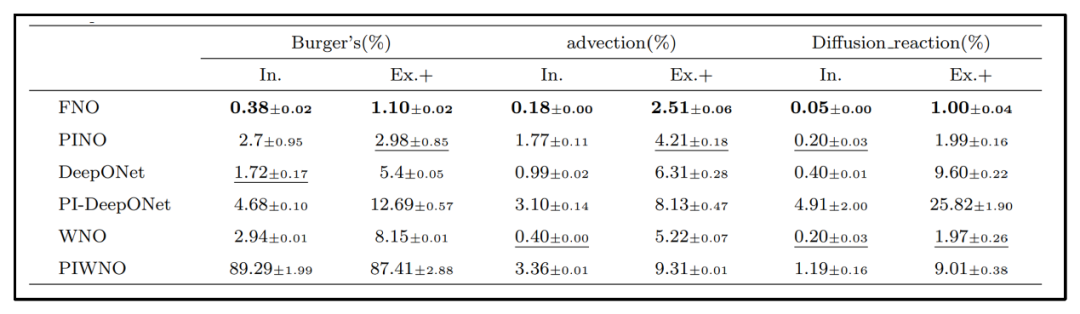
最后，为了检验插值与外推能力，论文在不同相关长度的高斯随机场进行训练与测试数据的采样，具体实验结果如表6所示。当训练与测试数据来源于不同相关长度的高斯随机场（即真正的分布外预测）时，纯数据驱动算子的求解误差明显上升，而混合物理约束可部分缓解这种误差的增长，展现出更强的外推鲁棒性。结果表明，混合式训练能够在一定程度上缓解外推时的性能下降，但对对流方程而言，不同损失项间的竞争反而可能使求解精度降低。

总体来看，物理约束与数据驱动的结合，在带噪声、跨分辨率以及外推场景下都展现出了更好的稳健性和求解精度。然而，混合式损失函数往往包含多个相互制约的项，这导致训练过程更加非凸且易陷入局部最优。要进一步提升性能，需要在实际应用中为PDE导数选择更合适的数值或谱方法，以减小导数的不同计算方式带来的误差干扰。

3.3 复杂系统建模

现有的工作中，大部分算子方法只是处理了一些简单偏微分方程系统，而复杂系统中的神经算子在实际应用时会面临不规则网格、多尺度和多输入等挑战，同时在不确定性量化、气候科学、工程和生物医药等领域有着广泛应用需求。因此许多算子研究关注这些复杂现实应用，设计了更加有效泛化的算子架构。

3.3.1 不规则网格

许多高性能神经算子要求输入输出在等距规则网格上进行离散，无法求解定义在不规则网格上的问题，极大的限制了其应用范围。例如，FNO因为依赖FFT而只能处理矩形均匀网格，尽管可以通过插值或将待解域嵌入更大矩形区来实现在不规则网格上的应用，但这种方式效率低且误差大。后来Li等人提出了Geo-FNO，将不规则网格映射到规则网格再进行处理；Geo-LNO则利用拉普拉斯算子的特性实现了在复杂几何上的离散不变性。DeepONet可在任意坐标点上预测，但缺乏离散不变性，于是BelNet(Basis Enhanced Learning Network) 融合了DeepONet的网格自由度和FNO的离散不变性，使其既能在不规则网格上使用，又能保持网格独立。OFormer(Operator Transformer) 则引入自注意力和交叉注意力机制，使得其能够灵活处理任意输入点和网格类型。

3.3.2 多尺度问题

多尺度系统中不同层级之间的耦合与振荡行为难以用单一尺度模型捕捉。多尺度DeepONet在分支和主干网络中都采用了多分辨率结构，对振荡算子进行了有效表示；同时，通过与传统数值求解器耦合，利用DeepONet替代高保真模型降低了多尺度模拟的代价。U-FNO在傅里叶层中嵌入了U-Net结构，可以更好地捕获多相流中的相互作用，但失去了离散不变性；IFNO(Implicit Fourier Neural Operator)以隐式映射方式提升了在多尺度问题中的稳定性；MNO(Multiscale Neural Operator)将神经算子与大尺度多尺度模型组合，利用算子学习传播误差，实现了高效的可微求解器；HT-Net(Hierarchical Transformer Network)和HANO(Hierarchical Attention Neural Operator) 分别基于层次化Transformer，自动分解多尺度结构，以线性或分层注意力捕获振荡特征，并保持了线性计算成本。

3.3.3 多输入算子

现实问题的输入往往是多种函数（如边界形状、全局参数向量等），原始的DeepONet等模型只能处理单一函数空间之间的映射。针对多输入场景，MIONet(Multi-input DeepONet) 使用多个独立分支网络分别编码每个函数，再与主干网络的输出结合，可分为高秩和低秩两种组合形式。Fourier-MIONet在多相流孔隙介质建模任务中显著降低了计算资源而无精度损失；D2NO(Distributed Deep Neural Operator) 采用分布式分支网络，进一步提高了效率。MultiAutoDeepONet将自动编码器与DeepONet结合，通过非线性降维和多分辨率处理，成功应对高维随机微分方程。

3.3.4 不确定性量化

在实际应用中，算子学习受到观测噪声（测量误差、传感器精度、缺失数据）和模型简化假设带来的不确定性影响，尤其在进行混沌系统的长期预测时误差会迅速放大。因此，量化预测置信度对构建可信算子至关重要。

一种常见方式是对网络参数做贝叶斯推断，以估计模型的不确定性。B‑DeepONet (Bayesian DeepONet) 通过复制交换Langevin扩散并行探索损失景观增强对噪声的鲁棒性，VB‑DeepONet (Variational Bayes DeepONet) 用变分推断近似后验分布，而集合卡尔曼反演（Ensemble Kalman Inversion, EKI）则无需计算导数即可在有限数据下高效估计不确定度。另一条思路是将神经算子与高斯过程（Gaussian Process, GP）结合，既可保留算子的表达能力，又能获得可解释的置信区间。NOGaP (Neural Operator-induced Gaussian Process) 直接将算子嵌入GP内核，设计诱导核并与GP超参数联合训练，实现了分辨率无关且可外推的高维PDE不确定性推断；还可通过最大似然或PDE残差同时进行数据驱动和物理驱动训练。第三类方法则是借鉴生成式与扩散模型，直接在训练中用评分规则或扩散采样生成函数空间的多模态分布。概率神经算子（Probabilistic Neural Operator , PNO）和扩散算子模型不仅能给出前向预测的不确定度，还可处理逆问题。

总体来看，贝叶斯训练、GP混合与生成式扩散三条主线共同推动了神经算子不确定性量化的发展，使其在高风险和数据稀缺场景下更加可靠。

3.3.5 真实应用

神经算子如今已发展为应对复杂物理系统的通用替代模型，在气候科学、工程仿真和生物医学领域带来了前所未有的速度与泛化能力提升。

气候领域中，将小波变换融入积分核的WNO能同时兼顾时间和空间的高分辨率；为克服地球球面几何造成的伪影，研究者在传统FNO基础上构建了球面卷积与多重网格架构，从SFNO(Spherical Fourier Neural Operator) 到更高效的SMgNO(Spherical Multigrid Neural Operator)，既保证了预报精度，又显著降低了计算开销；FourCastNet基于自适应FNO实现的全球中期天气预报，比传统数值模式推理速度快五个数量级，并可在无需重训练的前提下由粗糙模拟自动生成任意分辨率下的细节；DeepONet驱动的偏差校正模块和专门针对极端污染事件的CoNOAir (Complex Neural Operator for Air Quality) 模型，分别在气候模式矫正和城市空气质量实时预报中取得了超越传统方法的表现；在碳封存模拟方面，Nested FNO(Nested Fourier Neural Operator)、INO(Improved Neural Operator)、GFNO(Gabor-Filtered Fourier Neural Operator)等模型结合多保真度策略，实现了百万倍级的加速和超八成的数据需求削减，同时保持三维CO₂迁移预测的高精度；NMO (Neural Manifold Operator)等流形学习算子更通过捕捉环境系统的内在维度，为海洋动力学和大气层模拟提供了既精确又符合物理规律的新思路。

算子在工程领域的应用同样令人瞩目。DeepM&Mnet与SPI‑MIONet等框架能够在仅有稀疏观测数据情况下，快速完成电对流和液压压裂过程的多物理耦合仿真，并支持前后向算子循环以重建复杂边界层扰动；MFEAFNet(Multiscale Feature Extraction and Aggregation–Embedded FNO)、MIFNO(Multiple-Input FNO)、F‑FNO、B‑FNO等多种增强型FNO架构，通过集成多尺度特征提取、分解或边界元方法，在三维地震和弹性波场模拟中兼顾高保真与低内存需求；En‑DeepONet和FC‑DeepONet在地震震源定位和行波时差预测方面实现了四到五个数量级的精度提升；在固体力学与材料建模领域，IFNO(Implicit Fourier Neural Operator)、TherINO(Thermodynamically-informed Iterative Neural Operator)、PNO(Peridynamic Neural Operator) 以及基于ResUNet的深度DeepONet能直接从数字图像相关实验数据中学习非局部本构关系，并在脆性断裂、增材制造等场景下超过传统有限元方法；U‑FNO和注意力增强FNO将高雷诺数多相湍流仿真的训练数据量降至传统CNN的三分之一；Geom‑DeepONet、BAFNO(Boundary Assimilation FNO) 则进一步将几何参数化和边界条件自然融入网络，显著加快了飞行器、车体等复杂三维设计的优化迭代；新一代PI‑DeepONet (Physics-Informed DeepONet) 通过非线性解码和物理先验学习拓宽了航空航天设计空间的适用性。

在生物医学领域，神经算子为个性化医疗与实时成像带来新契机。基于有限元生长‑重塑模拟的DeepONet能对动脉瘤扩张和主动脉夹层进行风险预测，为临床决策提供实时支持；MAWNO(Multiscale Attention Wavelet Neural Operator) 将小波变换与自注意力结合，实现对突变式生化信号通路的精细刻画；无需预设本构模型的DeepONet本构学习方法直接从DIC(digital image correlation) 实验数据中获取组织应力‑应变关系，在肿瘤组织和心瓣膜等复杂生物材料模拟中具备更高可靠性；结合微观颗粒动力学的DeepONet血栓模拟可在亚百分比误差内再现血小板形变与应力累积；在医学成像方面，NBSO(Neural Born Series Operator)和小波算子分别加速了超声计算断层和弹性成像，实现近实时的肿瘤硬度映射；几何感知FNO在导管头部设计中指导结构优化，可有效减少临床细菌污染。

整体来看，神经算子通过端到端的算子学习，在气候预报、工程仿真与生物医学模拟等领域实现了前所未有的速度提升、精度突破与可扩展性增强。它们不仅加快了科学研究和工业设计的迭代速度，也为个性化医疗与实时监测等应用提供了可行路径。未来，随着更高效的网络结构和更丰富的物理先验的融入，神经算子有望在更多跨学科场景中发挥核心作用。

3.3.6 复杂系统实验

为了分析复杂系统中不同算子模型的性能，如表7所示，论文的实验选取了八个具有不同特征的PDE基准数据集，包含了不规则网格、多尺度、多输入等问题，在单张RTX 4090 GPU上对多种神经算子的相对误差进行了对比。

表7 复杂系统实验的PDE基准数据集

从表8的实验结果可以看出，针对规则网格问题（如Darcy流），FNO系列方法凭借极高的计算效率和良好的预测精度具有最佳性价比。虽然GK‑Transformer在性能上稍有优势，但其训练时间远超FNO，因此在多数场景下并不划算。对于高维湍流（Navier–Stokes方程）等复杂动力学问题，FNO同样能够取得最优或近似最优的结果，并且运行速度远快于Transformer架构。当处理不规则网格、多尺度或几何结构复杂的数据集（例如NACA翼型、二维Navier–Stokes变体以及复杂电感问题）时，GNOT的表现最为出色。得益于其交叉注意力机制，GNOT不仅能够同时捕捉异构输入之间的依赖关系，而且随着训练数据规模和模型容量的增加，其求解误差持续下降；当然，这也意味着它对训练时间和计算资源的需求更高。

表8 复杂系统实验对比结果

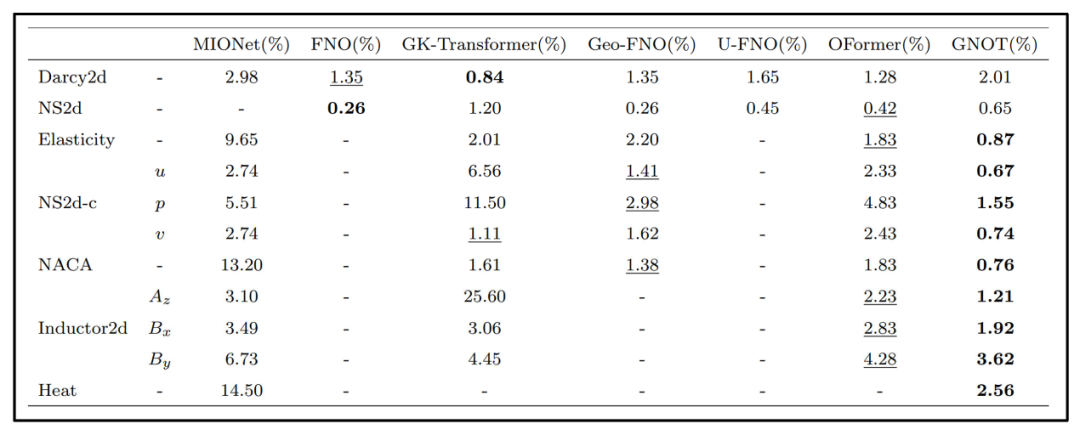
通过实验结果可知，针对常规问题（规则网格、低维PDE系统），考虑到速度与精度的优势，可优先选用FNO；针对复杂场景（非规则网格、多尺度、多输入），则建议使用GNOT等Transformer架构，以换取更高的精度，当然，前提是有充足的数据和算力支持。

四、总结与展望

尽管神经算子在求解PDE方面取得了诸多进展，但要让它们在更广泛的科学与工程应用中发挥作用，仍有若干关键方向值得深入：

算子基底的选择与改进。基底函数直接决定算子的表达能力——傅里叶基、小波基、拉普拉斯基等各有优势。未来可以探索更多类型的基底（如径向基函数、不同小波族），甚至针对特定PDE设计自适应混合基底，以提升对瞬态、局部不连续或多尺度行为的捕捉。

物理信息与数据驱动的深度融合。纯数据驱动需要海量高精度样本，纯物理驱动（PINN）常面临训练不收敛或超参数难以调试等问题。混合算子将物理残差、边界/初始条件与数据监督同时纳入损失，既提高了数据效率，也强化了物理一致性。但非凸损失、权重分配与优化器选择仍是瓶颈，需要专门针对混合框架的优化算法和高效PDE导数计算方法。

数据分布与采样策略。 目前大多数算子在高斯随机场等人工分布上训练，但真实场景的数据分布往往更复杂。研究不同数据分布对算子性能的影响、开发自适应采样或多物理预训练（MPP）方法，以及构建大规模通用的可迁移算子框架，都是亟待解决的课题。

跨领域模型与数值方法融合。将经典数值方法（有限元、多尺度迭代）与神经算子耦合，可兼顾物理精度与高效性；引入Transformer、扩散模型、Vision Transformer、状态空间模型等前沿架构，也有望增强算子的表达与建模能力。融合不同领域的技术，将催生更强大的通用算子。

软件工具与标准数据集。类似PINN代码库的DeepXDE/PINNacle的生态尚未在算子领域形成。亟需一套涵盖多学科、多类型PDE（线性/非线性、稳态/时变、高维/低维、光滑/粗糙解、规则/复杂几何）的标准数据集与基准库，以便不同算子架构的优势与适用范围的客观比较。