快速通关二叉树秘籍（下）

在前面我们讲了底层是数组的二叉树，今天讲以链表为底层的链式二叉树。

1. 链式二叉树基本结构

typedef int BTDataType;
typedef struct BinaryTreeNode
{int data;struct TreeNode* left;struct TreeNode* right;
}BTNode;

注意：由于链式二叉树的限制太少了，一般不进行数据的插入，因为在任意位置都能插入/删除数据，限制太少，意义小。 

2. 手动创建链式二叉树

BTNode* BuyNode(int data)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail!");exit(1);}node->data = data;node->left = node->right = NULL;return node;
}void test()
{BTNode BT;BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->left = node2;node1->right = node3;node2->left = node4;node3->left = node5;node3->right = node6;BTNode* root = node1;
}

3. 前中后序遍历

二叉树的数据查找离不开二叉树的遍历，二叉树的遍历方式有三种。

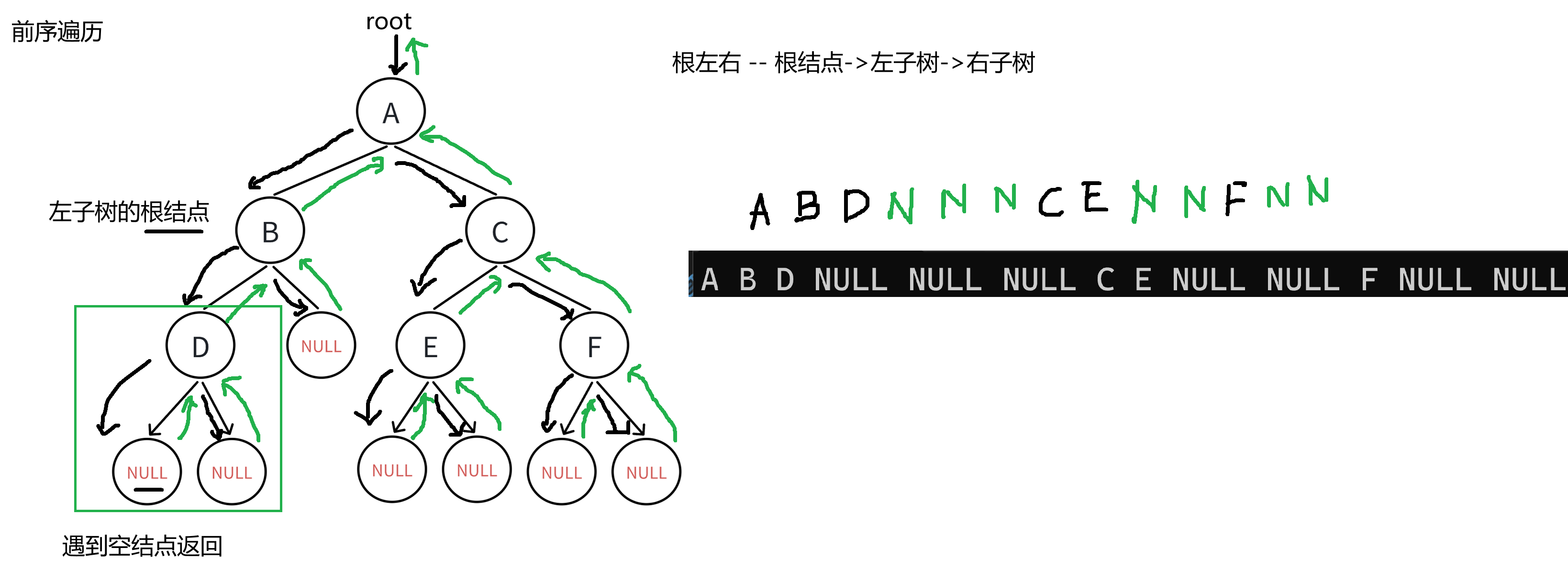
3.1 前序遍历

什么是前序遍历，前序遍历就是从根结点开始遍历，再遍历根结点的左子树，最后遍历根结点的右子树，即遍历顺序为根左右。

• 二叉树是由根结点，左子树和右子树构成，从根结点开始遍历，遍历到左子树，而左子树又是一棵二叉树，同理不断地递归，直到没有子树。
• 遍历二叉树的本质是递归。
• 这里前中后序遍历：主要是根结点的遍历的顺序。

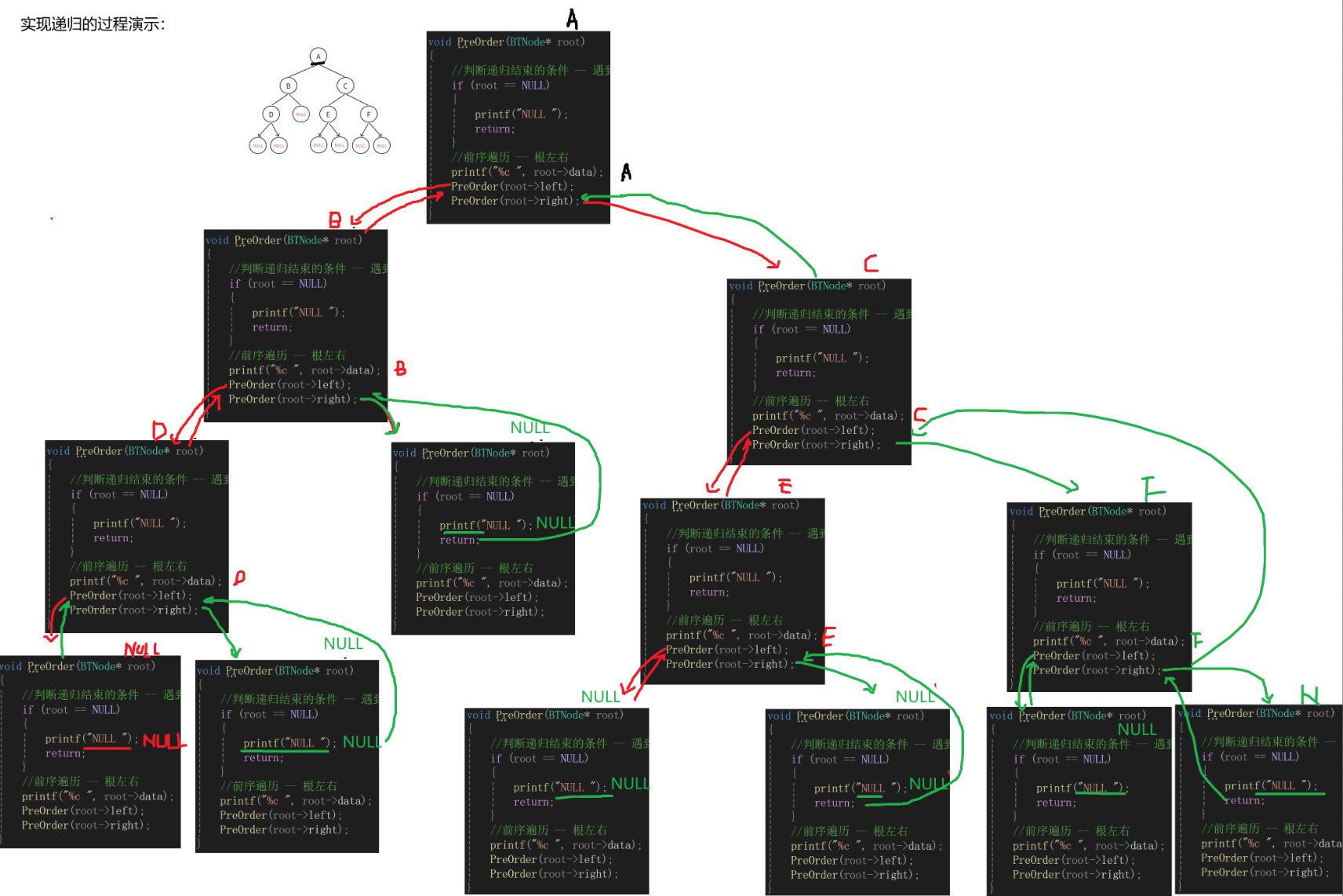
void PreOrder(BTNode* root)
{//判断递归结束的条件 -- 遇到空结点返回if (root == NULL){printf("NULL ");return;}//前序遍历 -- 根左右printf("%c ", root->data);PreOrder(root->left);PreOrder(root->right);
}

3.2 中序遍历 

中序遍历：即先遍历左子树，再遍历根结点，最后遍历右子树。

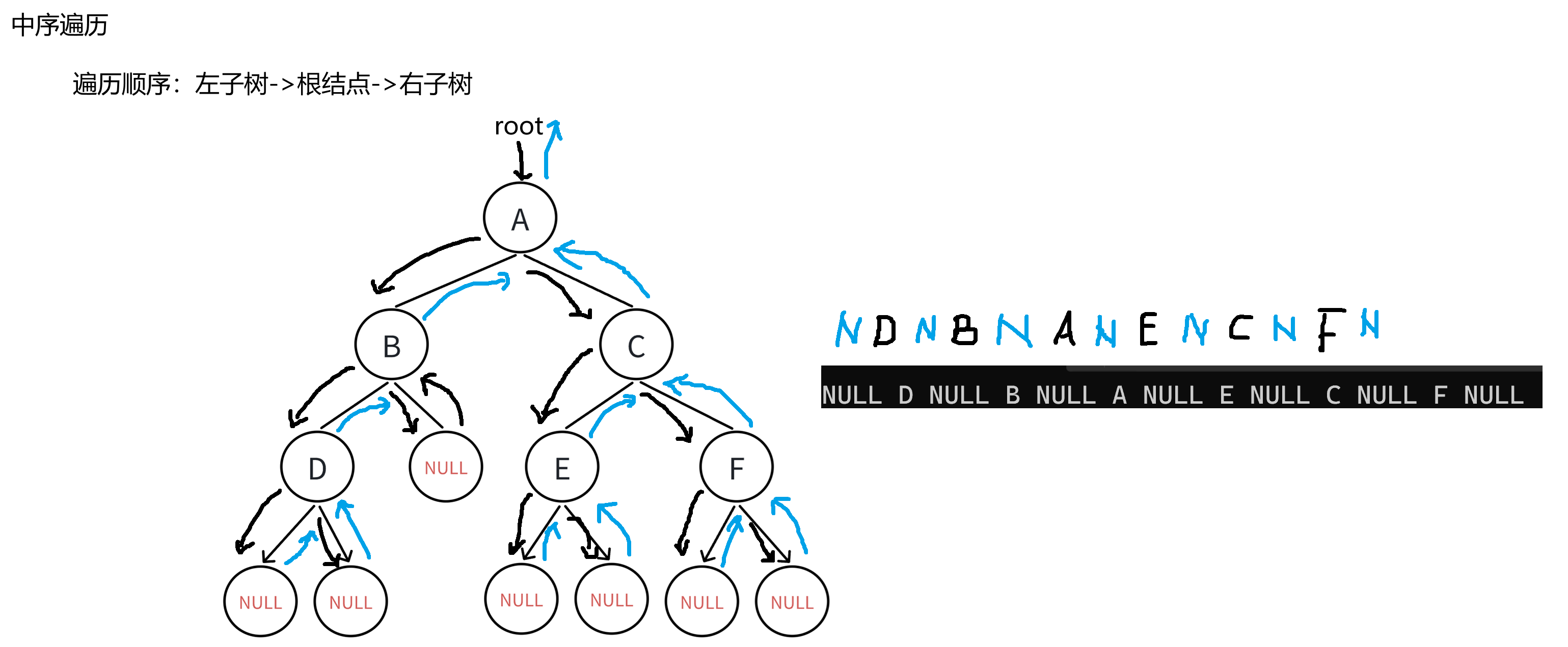
//中序遍历
void InOrder(BTNode* root)
{if(root== NULL){printf("NULL ");return;}//左子树->根结点->右子树InOrder(root->left);printf("%c ", root->data);InOrder(root->right);
}

3.3 后序遍历 

后序遍历：即先遍历左子树，再遍历右子树，最后遍历根结点。

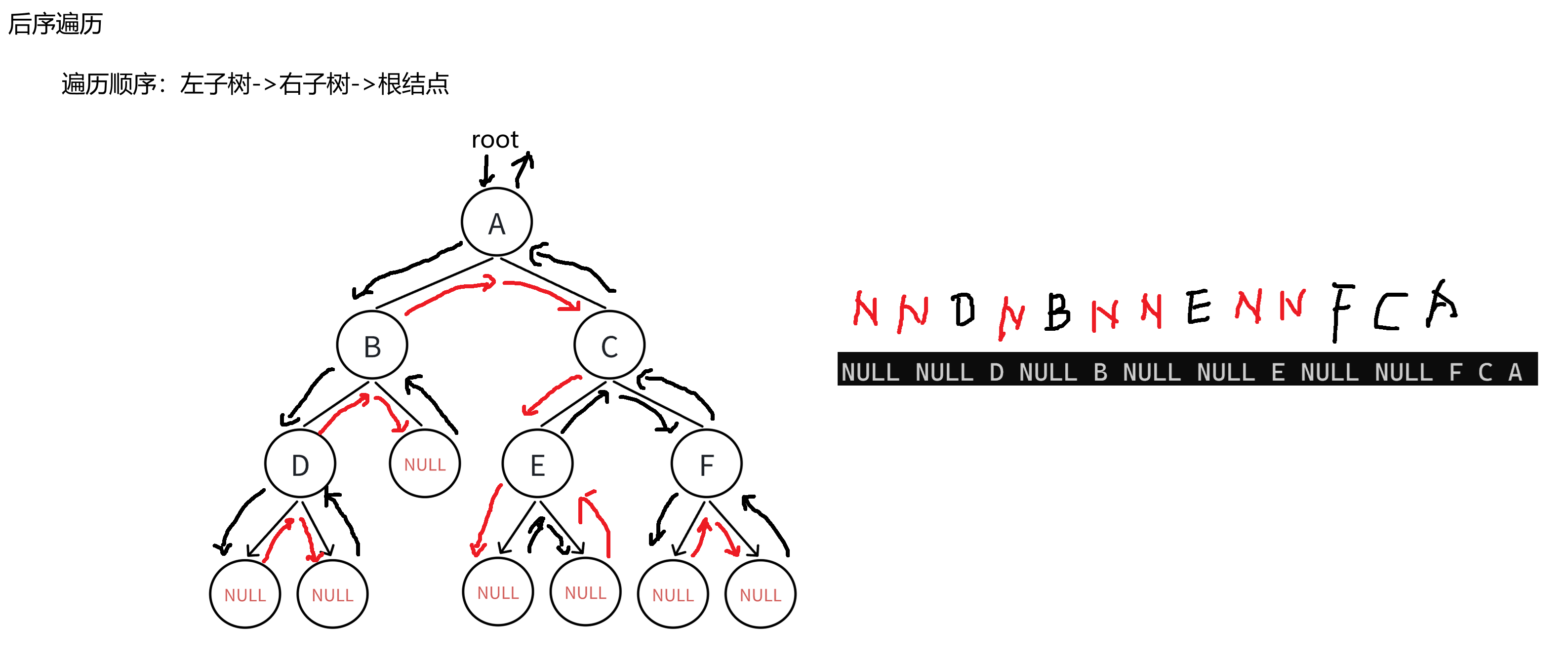
//后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}//左子树->右子树->根结点PostOrder(root->left);PostOrder(root->right);printf("%c ", root->data);
}

4. 结点个数以及高度

4.1 结点个数

已知：二叉树是由根结点，左子树和右子树组成。

那是否意味：我只要知道左子树的结点个数和右子树的结点个数？

而左子树又相当于一棵子树，又是由根结点，左子树和右子树构成！

这时你会发现一个规律：根结点+左子树结点个数+右子树结点个数=总结点个数

有了规律我们就可以使用递归来解决问题！

// ⼆叉树结点个数
int BinaryTreeSize(BTNode* root)
{if(root==NULL){return 0;}return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

有同学提出了另一种想法：我只要遍历的结点不为空结点，我就利用变量count++，最后返回count的值不就行了?

这个想法好像也对欸，我们试一试！

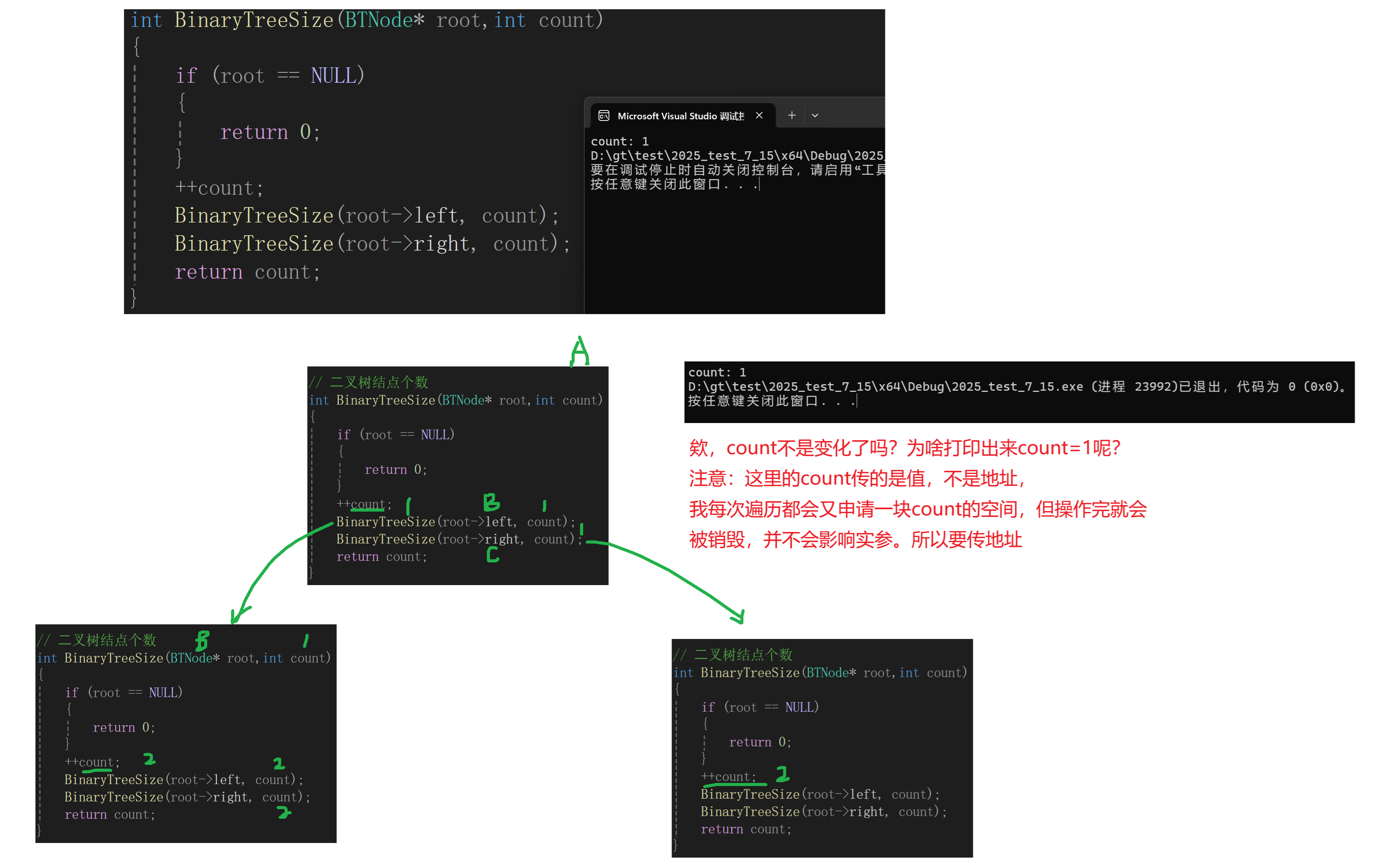
 改成传地址

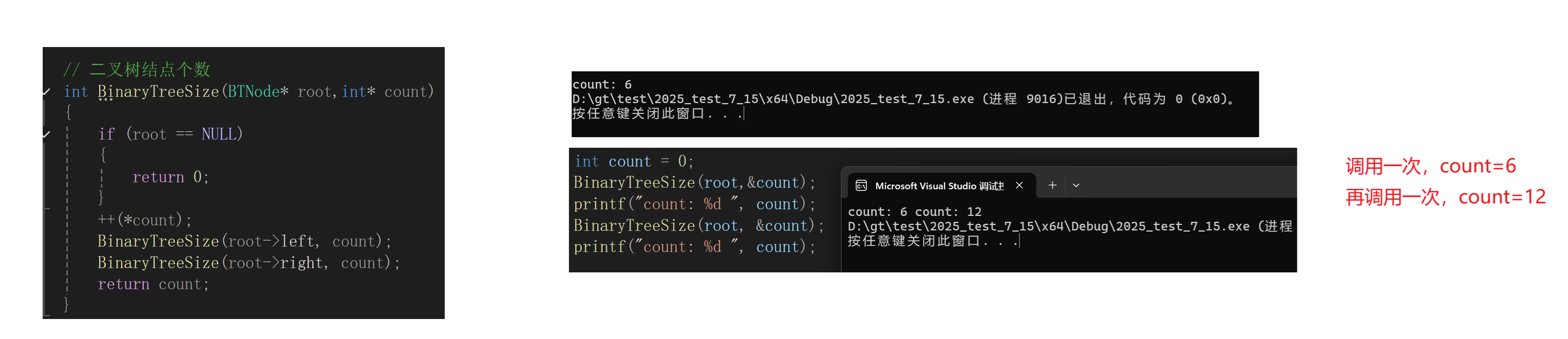
传地址最好是调用一次，如果多次调用，count会累加!

4.2 二叉树叶子节点个数

回顾上一节的叶子结点：即没有左右孩子（左右孩子=NULL）

那跟上面的思考是一样的：左子树叶子结点个数+右子树结点个数=总叶子结点个数。

// ⼆叉树叶⼦结点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if(root->left==NULL&&root->right==NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

4.3 二叉树第K层结点个数

既然要找第K层结点的个数，那么在传参的时候，就得知道K的值，那怎么找是不是第K层呢？

从第一层开始找，只要不是K=1，k--；只要K=1，就返回。

同理跟上面的思路一样：找左子树第K层结点个数+右子树第K层结点个数

不断地往下递归，直到K=1，返回1。

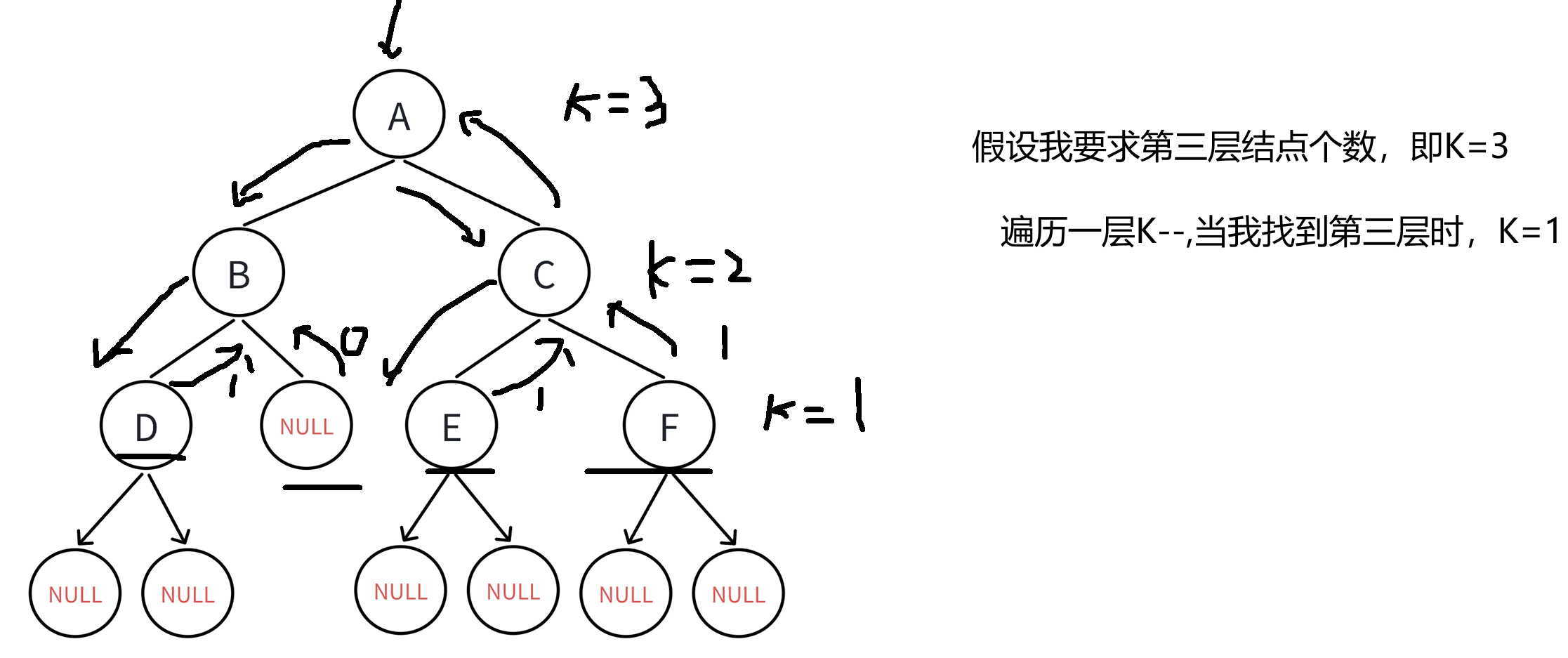
//⼆叉树第k层结点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

4.4 二叉树的深度/高度 

我们知道：二叉树的根结点为1层，再去遍历左右子树的层数

这里如果左右子树层数不一样，我们要得到他最大层数，所以遍历左右子树层数之后还需要比较。

即返回1+max(左，右子树层数）

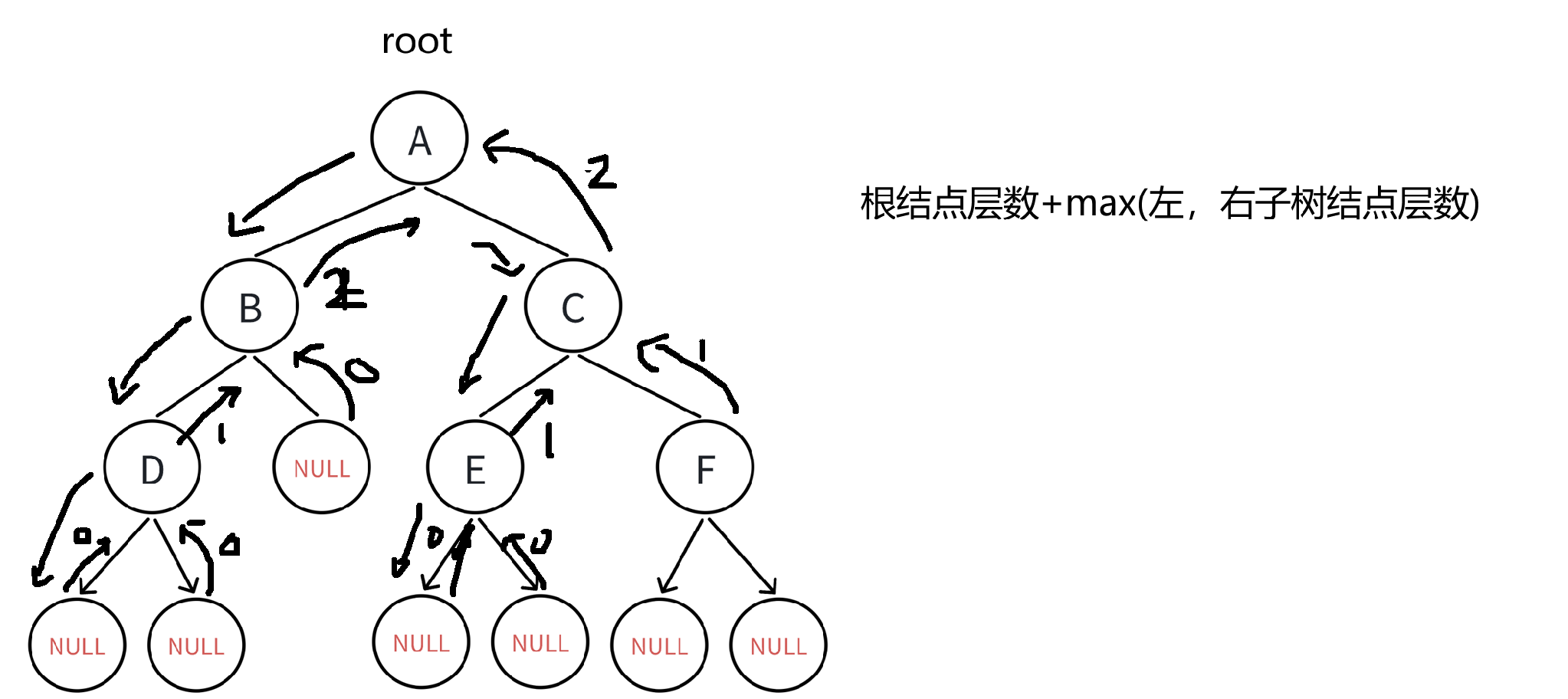
//⼆叉树的深度/⾼度
int BinaryTreeDepth(BTNode* root)
{if (root == NULL){return 0;}//左子树层数int left = BinaryTreeDepth(root->left);//右子树层数int right = BinaryTreeDepth(root->right);return 1 + (left > right ? left : right);
}

4.5 二叉树查找值为x的结点

遍历二叉树，在左子树查找值为x的结点，再到右子树查找值为x的结点，如果找到了，直接返回！

// ⼆叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if(root->data==x){return root;}int left = BinaryTreeFind(root->left, x);if (left){return left;}int right = BinaryTreeFind(root->right, x);if (right){return right;}//到这里说明没有找到return NULL;
}

4.6 二叉树销毁

这里销毁我们要从最后一个结点开始销毁，不能先销毁根结点

如果先销毁根结点，就无法找到后面的子树 ！！！这里就需要遍历二叉树销毁，就需要利用到前面的遍历方式，最好的就是后续遍历，最后销毁根结点。

//⼆叉树销毁
void BinaryTreeDestory(BTNode** root)//root发生改变
{if(*root==NULL){return;}BinaryTreeDestory(&((*root)->left));BinaryTreeDestory(&((*root)->right));free(*root);*root = NULL;
}

5. 层序遍历 

层序遍历是指首先访问第一层的树根结点，然后从左到右访问第2 层上的结点，接着是第三层的结点，以此类推，自上而下，自左至右逐层访问树的结点的过程。

层序遍历需要借助数据结构 -- 队列。

看定义我有点看不懂，来看图。

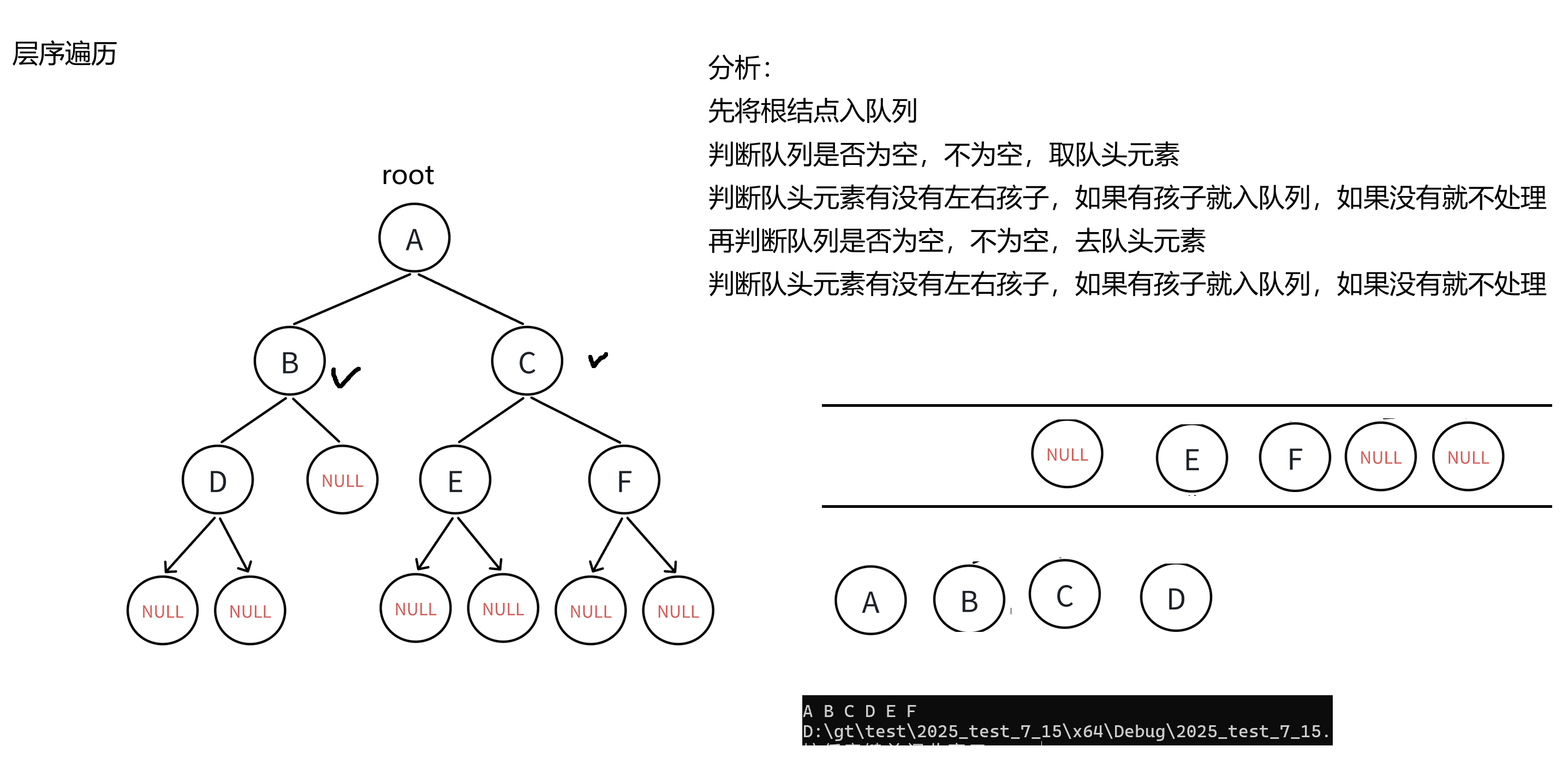
//层序遍历
void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);//将根结点入队列QueuePush(&q, root);while (!QueueEmpty(&q)){//取队头元素BTNode* top = QueueFront(&q);QueuePop(&q);printf("%c ", top->data);//入左右孩子if (top->left){QueuePush(&q, top->left);}if (top->right){QueuePush(&q, top->right);}}QueueDestory(&q);
}

链式二叉树到这里就结束了！下次分享一些关于二叉树的OJ题目！敬请期待~