约数之和其中数论的作用

AcWing

1.约数之和

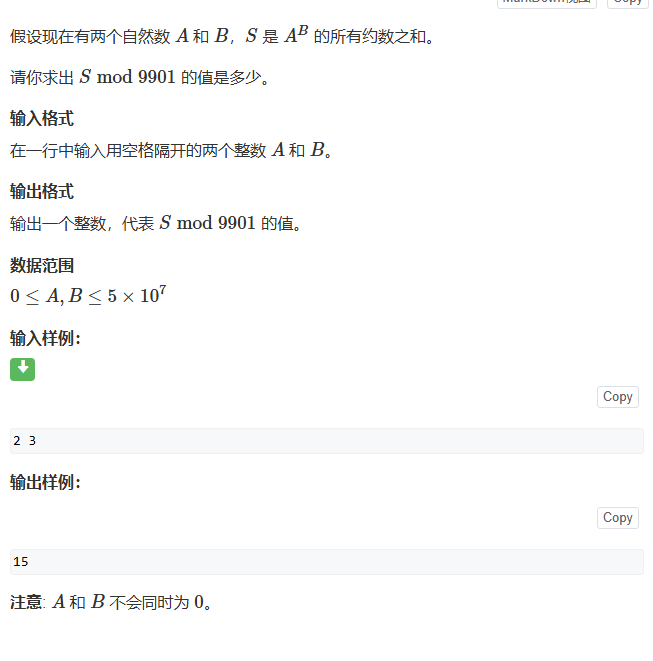
对于这一题，只能说不会，其中牵扯到了数论中的约数之和的问题

首先是对于该题的分解的过程与思路

快速幂模板

ll qmod(ll a, ll b) {ll sum = 1;while (b) {if (b & 1) sum = sum * a % mod; // 二进制位为1时，累乘结果a = a * a % mod; // 底数平方，准备下一位计算b >>= 1; // 右移一位，处理下一个二进制位}return sum;
}

质因数分解函数prime

void prime(ll x) {for (ll i = 2; i <= x / i; i++) { if (x % i == 0) { while (x % i == 0) { primes[i]++; // 统计质因数i的指数x /= i; }}}if (x > 1) primes[x]++; // 处理剩余大质数
}

等比数列求和函数sum

ll sum(ll p, ll k) {if (k == 1) return 1; // 递归边界：指数为1时，和为1（对应等比数列首项1）if (k % 2 == 0) { // 偶数项：1 + p + p² + ... + p^k = (1 + p^(k/2)) * (1 + p + ... + p^(k/2 - 1)) return (qmod(p, k / 2) + 1) * sum(p, k / 2) % mod; }// 奇数项：1 + p + ... + p^k = (1 + p^(k-1)) + (1 + p + ... + p^(k-2)) return (qmod(p, k - 1) + sum(p, k - 1)) % mod; 
}

推理过程：

主函数

void solve() {ll a, b;cin >> a >> b;prime(a); // 分解A的质因数ll ans = 1;for (auto i : primes) { ll p = i.first, k = i.second * b; // 质因数p，对应指数c*Bans = ans * sum(p, k + 1) % mod; // 累乘各质因数的等比数列和}if (a == 0) ans = 0; // 特殊情况：A=0时，0^B（B>0）无意义，结果为0cout << ans << endl;
}

完整代码

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0) // 加速输入输出
#define ll long long
#define endl '\n'const ll N=1e6+10;
const ll mod=9901;          // 结果取模 9901
unordered_map<ll,ll> primes; // 存储质因数分解结果// 快速幂：计算 a^b % mod
ll qmod(ll a, ll b) {ll res = 1;while(b) {if(b & 1) res = res * a % mod;a = a * a % mod;b >>= 1;}return res;
}// 质因数分解：将 x 分解为质因数及其指数
void prime(ll x) {for(ll i=2; i<=x/i; i++) {while(x % i == 0) {primes[i]++;x /= i;}}if(x > 1) primes[x]++; // 处理剩余的质因数
}// 等比数列求和：计算 1 + p + p^2 + ... + p^(k-1) % mod
ll sum(ll p, ll k) {if(k == 1) return 1;if(k % 2 == 0) {return (qmod(p, k/2) + 1) * sum(p, k/2) % mod;}return (qmod(p, k-1) + sum(p, k-1)) % mod;
}// 主函数：计算 A^B 的约数之和 % 9901
void solve() {ll a, b;cin >> a >> b;prime(a);       // 分解 A 的质因数ll ans = 1;for(auto [p, c] : primes) {ll k = c * b; // A^B 中质因数 p 的指数ans = ans * sum(p, k + 1) % mod; // 累乘每个质因数的等比数列和}if(a == 0) ans = 0; // 特殊处理 A=0 的情况cout << ans << endl;
}signed main() {IOS;solve();return 0;
}

知识补充(数论)

约数和公式

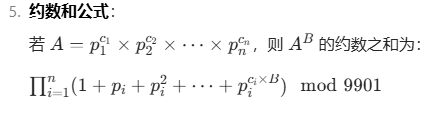
核心原理：

例子：