数据结构与算法:动态规划dp:背包问题:理论基础(状态压缩/滚动数组)和相关力扣题(416. 分割等和子集、1049.最后一块石头的重量Ⅱ、494.目标和)
背包问题
01背包理论基础
对于01背包问题,物品下标为0到i,对应的重量为weight[0]到weight[i],价值为value[0]到value[i],每个物品只可以取或不取,背包最大容量为j的场景。
常见的状态转移方程如下:
dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])
其中,dp[i][j]的含义是:对于下标0到i的物品,任意取放,满足背包剩余最大容量为j的情况下能获得的最大价值。
那么dp[i][j]可以划分为两种情况
- 取了下标为
i的物品,其获得的最大价值为dp[i-1][j-weight[i]]+value[i] - 没有取下标为
i的物品,其获得的最大价值为dp[i-1][j]
对于该数组的初始化,需要初始化i或j分别为0的边界情况:
i=0的情况:如果j >= weight[0],则我们可以取物品0,此时dp[0][j] = value[0]。否则,我们无法放入物品0,此时dp[0][j] = 0。j=0的情况:都为0,因为背包容量为0时,无法装入任何物品。
而对于i和j都非零时的情况,我们可以初始化成一个随意的值,因为根据状态转移方程来看,它的数组与它本身没有关系,所以在dp数组赋值时都会被覆盖掉。
接着我们思考它的遍历顺序。
对于这种dp数组为二维数组的情况,两层for循环是可以颠倒位置的。因为无论是先遍历背包,还是先遍历物品,都能保障遍历dp[i][j]时,已经给dp[i-1][j]以及dp[i-1][j-weight[i]赋值了正确的数值了。
注意,对于所有01背包问题,都可以使用回溯算法来解决,对于每个物品取或不取,一共n个物品,那么算法的复杂度就是2的n次方。所以一般回溯会超时。
状态压缩(滚动数组)
而关于刚刚的场景,实际上我们还可以用一维数组来做,也就是常说的状态压缩,或者说滚动数组。
此时状态转移方程为dp[j]=max(dp[j],dp[j-weight[i]]+value[i])。
其中,dp[j]的含义是:任意取放物品,满足背包 剩余最大容量为j 的情况下能获得的最大价值。
和二维的情况一样,dp[j]可以划分为两种情况
- 取了下标为
i的物品,其获得的最大价值为dp[j-weight[i]]+value[i] - 没有取下标为
i的物品,其获得的最大价值为dp[j]
首先我们思考一个问题,为什么可以状态压缩?
这是因为从二维数组的状态转移方程,我们可以知道,dp[i]的数据只依赖dp[i-1]层的数据,譬如在计算dp[3]的时候,我们就不再需要存储dp[1]的数据了。这种只依赖于有限的数据的情况,我们都可以状态压缩。在这我们压缩成两行数据,一行是dp[i-1],一行是dp[i]。
接着我们思考这个dp数组的初始化。
j为0,代表对于下标0到i的物品,任意取放,背包最大容量为0时能获得的最大价值,毫无疑问,肯定都初始化为0。j非零,此时因为状态转移方程中我们给dp[j]赋值时,会比较其自身。所以应该初始化为一个负值。
然后就是遍历顺序。
虽然数组只有1层了,但是因为状态转移方程里还是有i存在的,所以遍历赋值还是有两层for循环的,外层是遍历物品,内层是遍历背包容量。而且必须先遍历物品,再遍历背包容量,且背包容量需要倒序遍历。
为什么背包容量需要倒序遍历呢?
如果正序遍历,dp[j - weight[i]]可能在同一轮更新后再次被使用,导致相当于选择了同一个物品多次,这就变成了完全背包问题。倒序遍历可以确保每个物品只被使用一次。
416. 分割等和子集
在这道题虽然没有明说物品的价值,但实际上物品的价值就是等于它本身的重量。这样题目就转化为了,遍历下标从0到i的物品,任意拿取(物品只能拿取1次),满足重量为ans的情况?
为此我们想到了01背包,dp[j]表示遍历下标从0到i的物品,任意拿取,满足重量为j。当dp[j]==ans,也就是存在满足重量为ans的情况,那么返回True
代码1:最套板子的一集
class Solution:def canPartition(self, nums: List[int]) -> bool:n = len(nums)ans = 0for i in range(n):ans += nums[i]if ans%2:return Falseans=int(ans/2)dp = [0] * (ans+1) for i in range(n):for j in range(ans, nums[i]-1, -1):dp[j] = max(dp[j-nums[i]]+nums[i], dp[j])if dp[ans]==ans:return Trueelse:return False
最原始的一版,纯套板子。效率:2370ms,击败13.38%
代码2:优化外层for循环
根据上面的代码我们可以看到,其实我们不需要循环下标i,我们只需要拿到数本身就好了,所以直接用for num in nums
class Solution:def canPartition(self, nums: List[int]) -> bool:n = len(nums)ans = 0for i in range(n):ans += nums[i]if ans%2:return Falseans=int(ans/2)dp = [0] * (ans+1) for num in nums:for j in range(ans, num-1, -1):dp[j] = max(dp[j-num]+num, dp[j])if dp[ans]==ans:return Trueelse:return False
效率:2253ms,击败18.18%。
代码3:优化其他条件减少代码量
class Solution:def canPartition(self, nums: List[int]) -> bool:n = len(nums)ans = sum(nums) # 优化点1:用sum函数减少for循环if ans%2:return Falseans=ans//2 # 优化点2,用//替代int转化dp = [0] * (ans+1) for num in nums:for j in range(ans, num-1, -1):dp[j] = max(dp[j-num]+num, dp[j])if dp[ans]==ans:return Truereturn False
效率:2547ms,击败8.48%
可以看到其实效率没有说提升,但是代码量会少,看起来更简洁。
代码4:优化初始化条件(效率最高)
对于代码3,我们还可以再优化。因为我们其实并不关心dp[ans]的值具体是多少,也就是说我们并不在意最终能满足题意的方案数是多少,我们只关心能不能满足,那么初始化dp数组时就可以不用数值,而是用布尔值。注意这里,根据dp数组的含义,那么dp[0]的初始化就一定是True
class Solution:def canPartition(self, nums: List[int]) -> bool:n = len(nums)ans = sum(nums)if ans%2:return Falseans=ans//2dp = [False] * (ans+1) dp[0] = Truefor num in nums:for j in range(ans, num-1, -1):if dp[j - num]:dp[j] = Truereturn dp[ans]
效率:563ms,击败75.46%
1049.最后一块石头的重量Ⅱ
这道题转化一下思路,就可以变成和416. 分割等和子集一样的问题。
因为我们知道,如果两堆石头的重量越相近,那么相撞后可以留下的重量就越小。
也是求 任取其中的石块,看背包能装下的这堆石块的最大重量 是否能越靠近目标数(整体重量的一半)。
class Solution:def lastStoneWeightII(self, stones: List[int]) -> int:n = len(stones)all_sum = sum(stones)ans = all_sum//2dp = [0] * (ans+1)for stone in stones:for j in range(ans, stone-1, -1):dp[j] = max(dp[j], dp[j-stone]+stone)return abs((all_sum - dp[ans])-dp[ans])
效率:19ms,击败74.61%
494.目标和
这道题最难想的可能是不知道它和动态规划有什么关系。第一时间想的估计都是回溯去遍历每个元素取或不取。
但实际上,这道题可以将所有元素分为两类,一类是前面加+的,一类是前面加-的。那么就和1049.最后一块石头的重量Ⅱ非常类似。我们设正数集合的总和为pos,负数集合的总和为neg,那么存在以下逻辑:
pos+neg = sum
pos-neg = target
为此,推出pos = (target+sum)//2
也就是说,相当于我们要遍历所有物品,任意取放,找到满足背包容量为(target+sum)/2的情况数是多少。
所以,dp[j]的含义为,遍历前i个物品,任意取放,满足背包容量为j的情况数。
那么首先关于边界条件的判断,就有两种:
- pos不是整数。因为数组都是整数,所以
pos也一定是整数。 - pos小于0,根据
pos的定义,应该是正数集合的总和,那么不可能小于0。
代码如下:
n = len(nums)
all_sum = sum(nums)if (target+all_sum)%2: # pos不是整数return 0pos= (target+all_sum)//2if pos< 0:# pos小于0return 0
其次,关于状态转移方程,dp[j]=dp[0]+dp[1]+dp[2]+...dp[j-1],也就是:
或者说dp[j]=dpj]+dp[j-nums[i]]或者说dp[j]+=dp[j-num]
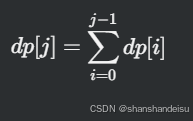
为什么是累加?
因为每个物品都可以选择取或不取,所以对于每个j,它的值是由所有可能的前一个状态转移而来的。具体来说,dp[j]的值是由dp[j-1]、dp[j-2]、…、dp[0]这些状态转移而来的,因为这些状态都可能在加入当前物品后达到j。
最后关于初始化,在这我们要求的dp是情况数,那么dp[0]应该是多少呢?
实际上,dp[0]应该是1。举个例子:
nums = [0],target = 0
那么pos应该为1,因为给0前面加上一个+是一种情况。
最后的代码如下:
class Solution:def findTargetSumWays(self, nums: List[int], target: int) -> int:n = len(nums)all_sum = sum(nums)if (target+all_sum)%2:return 0pos = (target+all_sum)//2if pos < 0:return 0dp = [0] * (pos+1)dp[0] = 1for num in nums:for j in range(pos, num-1, -1):dp[j] += dp[j-num]return dp[pos]效率:18ms,击败87.50%
总结
对于416. 分割等和子集,题目实际上为:给定一个重量为target的背包,是否能装满这个背包,转移方程为
dp[0] = True
for num in nums:for j in range(target, num-1, -1):if dp[j - num]:dp[j] = True
对于1049.最后一块石头的重量Ⅱ,题目实际上为:给定一个重量为target的背包,该背包能装的最大价值(价值就是重量)是多少? 转移方程为:
dp = [0] * (target+1)
for stone in stones:for j in range(target, stone-1, -1):dp[j] = max(dp[j], dp[j-stone]+stone)
对于494.目标和,题目实际上为:给定一个重量为target的背包,求装满这个背包的方案数是多少? 转移方程为:
dp = [0] * (target+1)
dp[0] = 1
for num in nums:for j in range(target, num-1, -1):dp[j] += dp[j-num]
