算法笔记—前缀和(动态规划)
【模板】前缀和_牛客题霸_牛客网 (nowcoder.com)
#include <initializer_list>
#include <iostream>
#include <vector>
using namespace std;int main() {//输入数据int n,q;cin>>n>>q;vector<int> arr;arr.resize(n+1);for(int i=1;i<n+1;i++){cin>>arr[i];}//构建前缀和vector<long long> dp;dp.resize(n+1);for(int i=1;i<n+1;i++){dp[i]=dp[i-1]+arr[i];}while(q--){int l,r;cin>>l>>r;cout<<dp[r]-dp[l-1]<<endl;}return 0;
}
// 64 位输出请用 printf("%lld")【模板】二维前缀和_牛客题霸_牛客网 (nowcoder.com)
#include <iostream>
#include <vector>
using namespace std;const int N=1001,M=1001;
int arrp[N][M]={0};
long long dp[N][M]={0};
int main(){int n,m,q;cin>>n>>m>>q;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>arrp[i][j];}}//前缀和for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){dp[i][j]=dp[i][j-1]+dp[i-1][j]-dp[i-1][j-1]+arrp[i][j];}}int x1,y1,x2,y2;while(q--){cin>>x1>>y1>>x2>>y2;cout<<dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]<<endl;}
}724. 寻找数组的中心下标 - 力扣(LeetCode)
class Solution {
public:int pivotIndex(vector<int>& nums) {const int n=nums.size();int dp1[n+1]; int dp2[n+1];dp1[0]=0;for(int i=1;i<n;i++){dp1[i]=dp1[i-1]+nums[i-1];}dp2[n-1]=0;for(int i=n-2;i>=0;i--){dp2[i]=dp2[i+1]+nums[i+1];}for(int i=0;i<n;i++){if(dp1[i]==dp2[i]){return i;}}return -1;}
};
238. 除自身以外数组的乘积 - 力扣(LeetCode)
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {int n=nums.size();vector<int> dp1(n);vector<int> dp2(n);dp1[0]=dp2[n-1]=1;for(int i=1;i<n;i++){dp1[i]=dp1[i-1]*nums[i-1];}for(int i=n-2;i>=0;i--){dp2[i]=dp2[i+1]*nums[i+1];}vector<int> ret(n);for(int i=0;i<n;i++){ret[i]=dp1[i]*dp2[i];}return ret;}
};560. 和为 K 的子数组 - 力扣(LeetCode)
class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int, int> hash;hash[0]=1;int sum = 0;int ret = 0;for (auto val : nums) {sum += val;if (hash.count(sum - k))ret += hash[sum - k];hash[sum]++;}return ret;}
};974. 和可被 K 整除的子数组 - 力扣(LeetCode)
同余定理:(a-b)%k==c………0 =》 a%k==b%k
暴力枚举:枚举每个以nums[i]结尾的数组,判断其中和为k的累加,最后返回结果
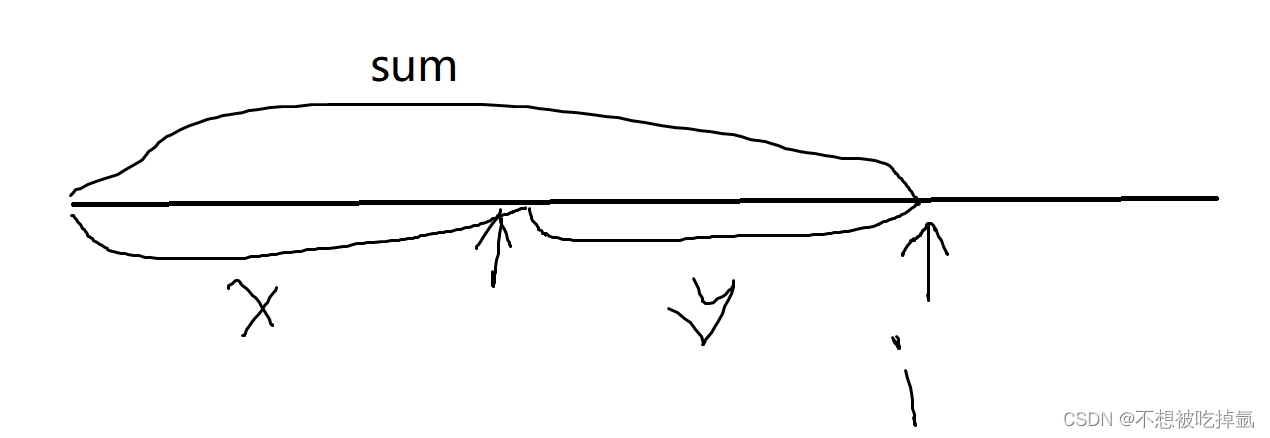
优化:前缀和+同余定理:首先,加以i结尾的子数组和为y,sum是i的前缀和,然后y%k==0表示子数组的和可以被整除。所以(sum-x)%k==0 => 同余定理: sum%k==x%k,其中x可以是i之前所有元素的前缀和,我们用hash统计好i之前所有元素的前缀和,就可以得出以i结尾的子数组和为k的个数。
细节:这里的sum和x可能为负数,所以%k取余可能是负数,所以用 sum%k==x%k,无法正确判断出一些特殊情况,例如sum=-3,x=2;所以修正取余:(sum%k+k)%k,这样所有余数都死正数。
class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {int ret=0;unordered_map<int,int> hash;int n=nums.size();hash[0]=1;int sum=0;for(int i=0;i<n;i++){sum+=nums[i];int r=(sum%k+k)%k;//根据同余定理,判断前缀和除以k所得余数r的个数if(hash.count(r)) ret+=hash[r];hash[r]++;}return ret;}
};. - 力扣(LeetCode)
class Solution {
public:int findMaxLength(vector<int>& nums) {int ret=-1;int n=nums.size();for(int i=0;i<n;i++){//0转换为-1。if(nums[i]==0)nums[i]=-1;}unordered_map<int,int> hash;//建立前缀和与下标的映射关系//我就是个大傻逼,前缀和都要有一个开始前缀hash[0]=-1;int sum=0;for(int i=0;i<n;i++){sum+=nums[i];if(hash.count(sum)) ret=max(ret,i-hash[sum]) ;//这里是sum-x,x是和为0的连续子数组的和.x=0hash[sum]=i;//建立下标和前缀和的映射}return ret;}
};. - 力扣(LeetCode)
//************************
class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m=mat.size(); int n=mat[0].size();vector<vector<int>> answer(m,vector<int>(n,0));vector<vector<int>> dp(m+1,vector<int>(n+1,0));for(int i=1;i<=m;i++){//构建前缀矩阵for(int j=1;j<=n;j++){dp[i][j]=dp[i][j-1]+dp[i-1][j]-dp[i-1][j-1]+mat[i-1][j-1];}}for(int i=0;i<m;i++){for(int j=0;j<n;j++){//Ⅰ用变量x1,y1存计算的区域,用条件判断太傻逼int x1= i-k>=0?i-k:0; int y1= j-k>=0? j-k:0;int x2= i+k<m? i+k:m-1; int y2= j+k<n ? j+k:n-1;x1++;y1++;x2++;y2++;//Ⅱ因为dp的位置坐标对于mat,+1answer[i][j]=dp[x2][y2]-dp[x2][y1-1]-dp[x1-1][y2]+dp[x1-1][y1-1];//Ⅲ 区间计算x1-1,y1-1}}return answer;}
};