线段数--算法
线段树是常用来维护 区间信息 的数据结构
线段树可以在 O(logN) 的时间复杂度内实现
- 单点修改
- 区间修改
- 区间查询
-
- 区间求和
- 求区间最大值
- 求区间最小值
简单介绍一下线段树
线段树是一个将区间内的数不断细分的一种数据结构,也就是一个完全二叉树,用每一个叶子节点代表一个区间内的值
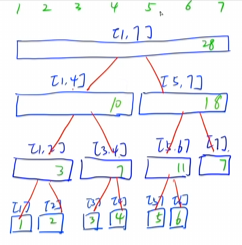
操作1:单点修改
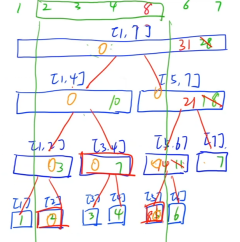
单点修改是找到要修改的那个点所在的每一层的区间,最后通过叶子节点,修改为相应的值,然后向上递归

操作2:区间查询
区间查询[l,r]是指在线段树内从上向下查询,如果子区间的左右端点都在[l,r]内则不用在向下递归,直到找到所有的点
常用操作函数
- pushup(int u):用子节点的信息更新当前节点
-
- 参数u是根节点
static void pushUp(int u){node[u].sum=node[u<<1].sum+node[u<<1|1].sum;
}- build(int u,int l,int r):在一段区间上初始化线段树
-
- 参数u是根节点,l是区间左端点,r是区间右端点
static void build(int u,int l,int r){if(l==r)node[u]=new Node(l,r,w[r]);else{node[u]=new Node(l,r,0);int mid=l+r>>1;build(u<<1,l,mid);build(u<<1|1,mid+1,r);pushUp(u);}
}- modify(int u,int x,int v):修改某一点的值
-
- 参数u是根节点,x是要修改的节点,v是要增加或减小的值
static void modify(int u,int x,int v){if(node[u].l==node[u].r)node[u].sum+=v;else{int mid=(node[u].l+node[u].r)>>1;if(x<=mid)modify(u<<1,x,v);else modify(u<<1|1,x,v);pushUp(u);}
}- query(int u,int l,int r):查询
-
- 参数u是根节点,l是区间左端点,r是区间右端点
static int query(int u,int l,int r){if(node[u].l>=l&&node[u].r<=r)return node[u].sum;int mid=node[u].l+node[u].r>>1;int sum=0;if(l<=mid)sum+=query(u<<1,l,r);if(r>mid)sum+=query(u<<1|1,l,r);return sum;
}节点表示
父节点:x/2 ==> x>>1
左儿子:2x ==> x<<1
右儿子:2x+1 ==> x>>1|1

动态求连续区间和
package 线段树;import java.io.BufferedReader;
import java.io.InputStreamReader;public class Main {static int N=1000010;static Node[] node=new Node[N];static int[] w=new int[N];static BufferedReader br=new BufferedReader(new InputStreamReader(System.in));static int n,m;static String[] $;static void pushUp(int u){node[u].sum=node[u<<1].sum+node[u<<1|1].sum;}static void build(int u,int l,int r){if(l==r)node[u]=new Node(l,r,w[r]);else{node[u]=new Node(l,r,0);int mid=l+r>>1;build(u<<1,l,mid);build(u<<1|1,mid+1,r);pushUp(u);}}static int query(int u,int l,int r){if(node[u].l>=l&&node[u].r<=r)return node[u].sum;int mid=node[u].l+node[u].r>>1;int sum=0;if(l<=mid)sum+=query(u<<1,l,r);if(r>mid)sum+=query(u<<1|1,l,r);return sum;}static void modify(int u,int x,int v){if(node[u].l==node[u].r)node[u].sum+=v;else{int mid=(node[u].l+node[u].r)>>1;if(x<=mid)modify(u<<1,x,v);else modify(u<<1|1,x,v);pushUp(u);}}public static void main(String[] args)throws Exception {$=br.readLine().split(" ");n=Integer.parseInt($[0]);m=Integer.parseInt($[1]);$=br.readLine().split(" ");for(int i=1;i<=n;i++)w[i]=Integer.parseInt($[i-1]);build(1,1,n);while (m-->0){$=br.readLine().split(" ");int k=Integer.parseInt($[0]);int a=Integer.parseInt($[1]);int b=Integer.parseInt($[2]);if(k==0)System.out.println(query(1,a,b));else modify(1,a,b);}}
}class Node{int l,r,sum;public Node(int l,int r,int sum){this.l=l;this.r=r;this.sum=sum;}
}