OPENCV判断图像中目标物位置及多目标物聚类
文章目录
在最近的项目中,又碰到一个有意思的问题需要通过图像算法来解决。就是显微拍摄的到的医疗图像中,有时候目标物比较偏,也就是在图像的比较偏的位置,需要通过移动样本,将目标物置于视野正中央,然后再次进行拍摄。
就类似于下面的图像:
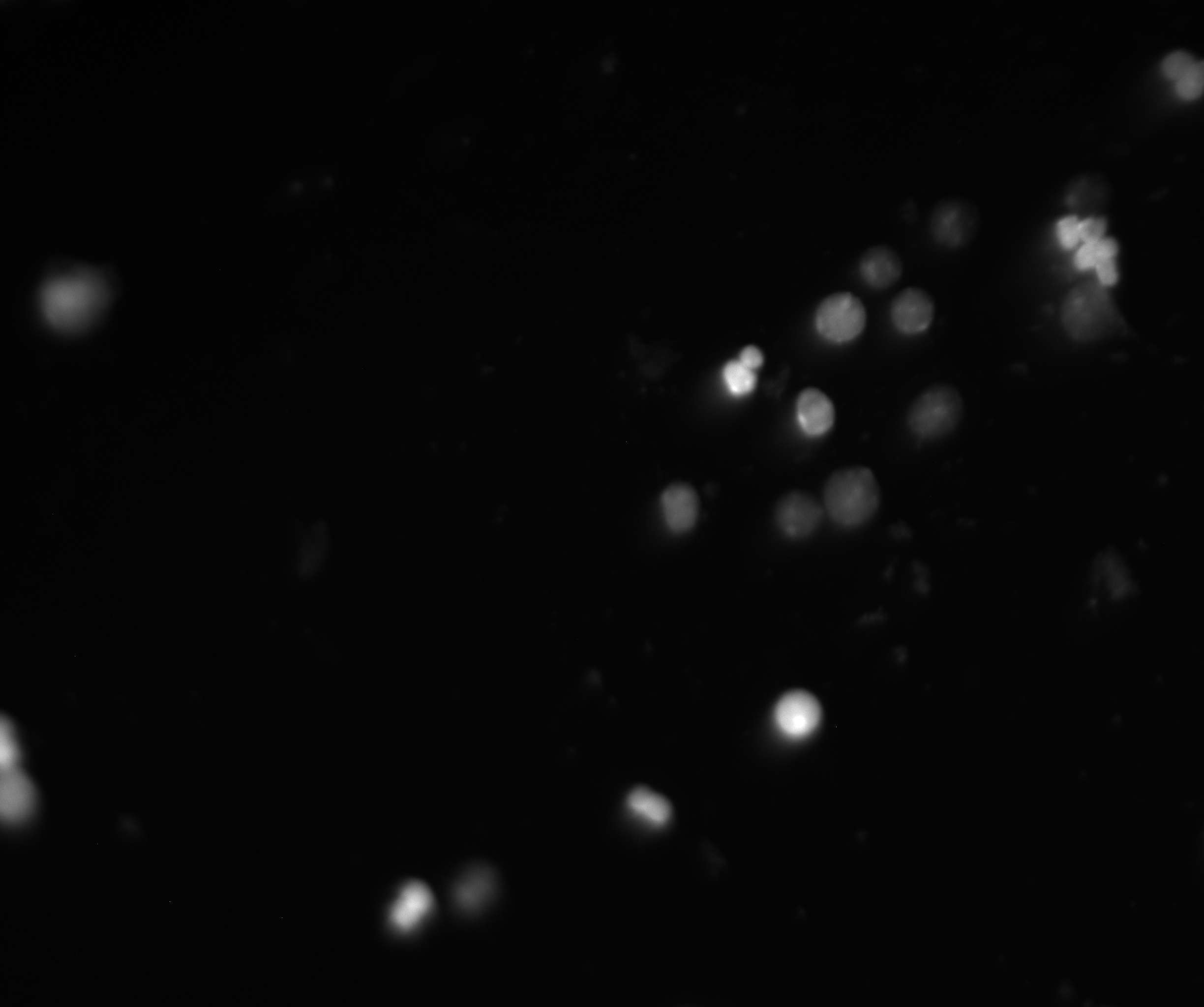
基于这个需求,在图像上就需要使用图像算法进行判断(没有必要使用深度网络的时候就不要用,太浪费资源了)。
对于上面的图像,基本的处理逻辑是:
- 因为目标物是细胞,也就是图中的一个一个的圈圈,需求就是要让尽可能多的细胞位于图像正中央。
- 目标物的粘连比较少,所以基于阈值分割的基本逻辑应该是可以将所需要的目标物提取出来(这一块在python的opencv操作记录11——阈值分割这一篇已经讲过了)。
- 分割完之后再通过opencv提取轮廓的方法将轮廓提取出来。
- 提取完轮廓之后,对每个轮廓求外接矩形。
- 利用业务特性对相应的轮廓做一些过滤操作。
- 将多个矩形做一个聚类,这里可以有多种聚类方案,可以先聚类再筛选,也可以根据某个逻辑确定一个质心,然后再根据这个质心再做聚类。
- 然后就是调参工作了。
我自己的代码为:
int getCenter(cv::Mat img, cv::Rect& resultRect)
{cv::cvtColor(img, img, cv::COLOR_RGB2GRAY);// 阈值分割cv::threshold(img, img, 50, 255, cv::THRESH_BINARY);// 提取轮廓std::vector<cv::Mat> contours;cv::findContours(img, contours, cv::RETR_LIST, cv::CHAIN_APPROX_NONE);// 逐步聚类的方法std::vector<float> xs, ys;// 初始化质心float centroid_x = 0.0f, centroid_y = 0.0f;// 找到第一个质心,我这里是使用面积最大的作为第一个质心,代码没有贴上来int maxIndex = 0;float maxSocre = 0.0f;// 迭代计算质心for (int i = 0; i < contours.size(); i++){score = cv::contourArea(contours[i]);// 判断是一个有效区域if (score > threshold_score){cv::Rect rect = cv::boundingRect(contours[i]);// 判断是否离中心比较远, 第一次不做判断if (abs(rect.x + (rect.width / 2) - centroid_x) > centroidThresholdX){continue;}if (abs(rect.y + (rect.height / 2) - centroid_y) > centroidThresholdY){continue;}// 纳入下一次的质心计算xs.push_back(rect.x + rect.width / 2);ys.push_back(rect.y + rect.height / 2);float tempCenterX = 0.0f;for (int x = 0; x < xs.size(); x++){tempCenterX += xs[x];}centroid_x = tempCenterX / xs.size();float tempCenterY = 0.0f;for (int y = 0; y < ys.size(); y++){tempCenterY += ys[y];}centroid_y = tempCenterY / ys.size();}}for(int z = 0; z < xs.size(); z++){ if (xs[z] < minX){minX = xs[z];}if (xs[z] > maxX){maxX = xs[z];}if (ys[z] < minY){minY = ys[z];}if (ys[z] > maxY){maxY = ys[z];}}std::cout << "maxX:" << maxX << "minX:" << minX << "maxY:" << maxY << "minY:" << minY << std::endl;resultRect.x = minX;resultRect.y = minY;resultRect.width = maxX - minX;resultRect.height = maxY - minY;return 0;
}
最后的结果是:
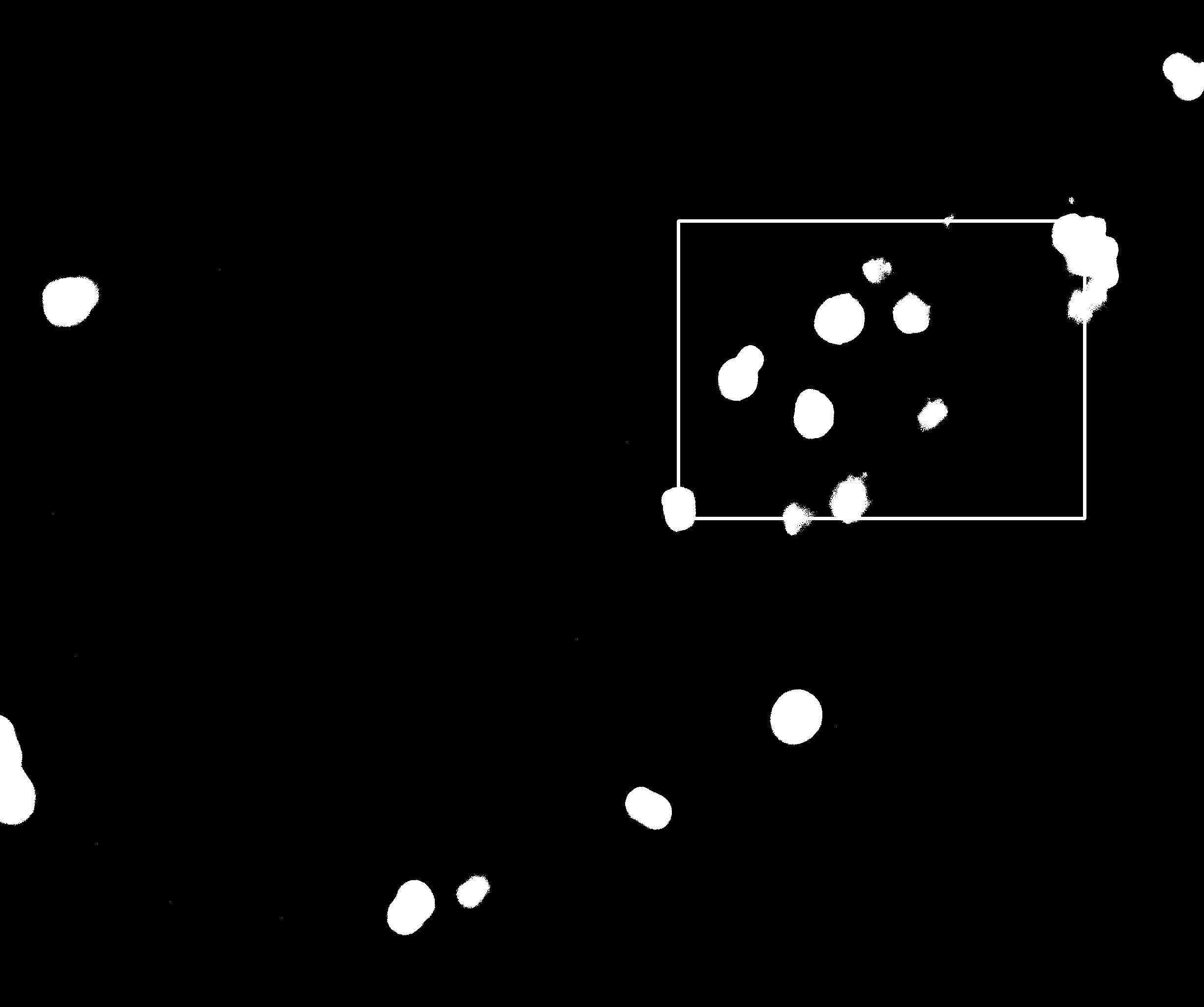
调整的距离就是这个矩形的中央到整个图像的中央坐标了。
