神经网络基础知识
神经网络基础知识
文章目录
- 神经网络基础知识
- 一、人工神经网络
- 1.激活函数
- sigmod函数
- Tanh函数
- Leaky Relu函数
- 分析
- 2.过拟合和欠拟合
- 二、学习与感知机
- 1.损失函数与代价函数
- 2. 线性回归和逻辑回归
- 3. 监督学习与无监督学习
- 三、优化
- 1.梯度下降法
- 2.随机梯度下降法(SGD)
- 3. 批量梯度下降法(BGD)
- 4.小批量梯度下降法(MBGD)
- 5.Momentum动量法
- 6.优化学习率/步长
- 7.反向传播算法
- 四、卷积神经网络
- 1.感受野
- 2.下采样(池化)
- 3.Flattening平整化
- 4.举例
- 五、循环神经网络
- 1. RNN的基本概念
- 2.LSTM长短期记忆网络
- 3.GRU
- 4.Attention注意力机制
- 5.Transformer模型
一、人工神经网络
1.激活函数
sigmod函数
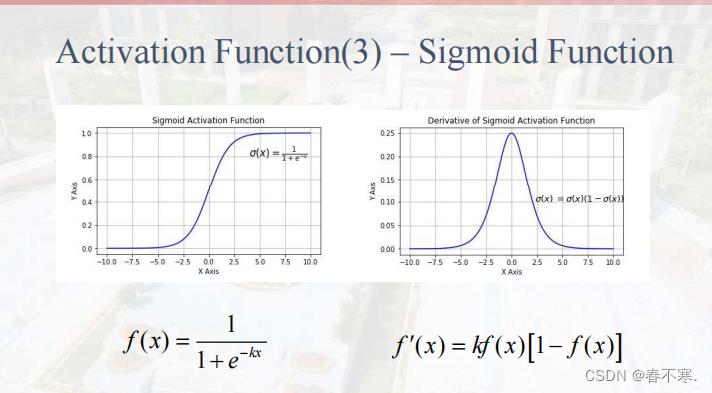
Tanh函数
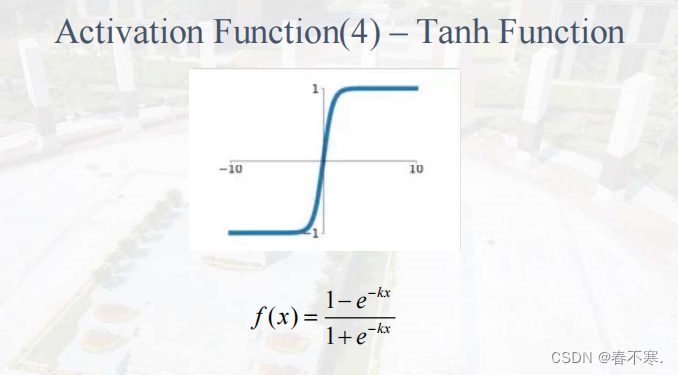
Leaky Relu函数
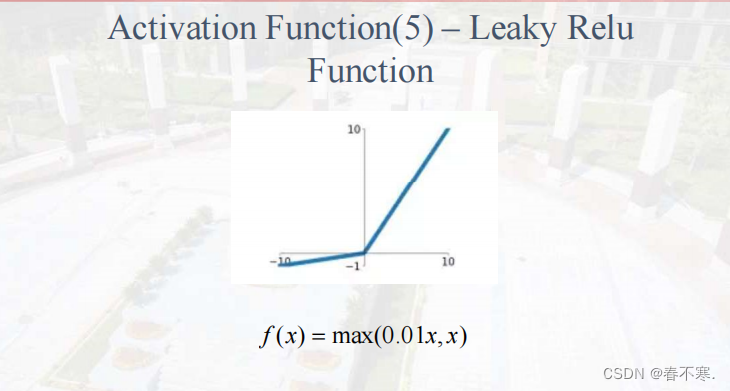
分析
- sigmod和Tanh函数为饱和函数,leaky Relu函数为非饱和函数,使用非饱和激活函数的优势在于:
- 非饱和函数能解决深度神经网络(层数非常多)的梯度消失问题,浅层网络才能使用sigmod作为激活函数。
- 非饱和函数能够加快收敛速度。
- 激活函数的作用是将ANN模型中一个节点的输入信号转换成一个输出信号,若不运用激活函数的话,则输出信号将仅仅是一个简单的线性函数。
2.过拟合和欠拟合
- 欠拟合是指模型在训练集、验证集和测试集上均表现不佳的情况;
- 过拟合是指模型在训练集上表现很好,到了验证和测试阶段就很差,即模型的泛化能力很差。
二、学习与感知机
1.损失函数与代价函数
- 代价(目标)函数是损失函数的平均值
- 输入x通过模型预测输出y,此过程称为向前传播,而将预测与真实值的差值减小需要更新模型中的参数,这个过程称为向后传播。
- 损失函数

- 代价函数C(x),若是有多个样本可以将所有代价函数的取值求均值,记作J(x)。优化参数x,最常用的方法就是梯度下降,就是对代价函数J(x)的偏导数。
- 代价函数

-
均方误差通常用在线性回归问题中,交叉熵代价函数通常用在分类问题中。
-
损失函数(Loss Function )是定义在单个样本上的,算的是一个样本的误差。
代价函数(Cost Function )是定义在整个训练集上的,是所有样本误差的平均,也就是损失函数的平均。
目标函数(Object Function)定义为:最终需要优化的函数。等于经验风险+结构风险(也就是Cost Function + 正则化项)。
2. 线性回归和逻辑回归
- 线性回归是回归问题(预测数值是连续型的),逻辑回归是分类问题(预测数值是离散型的)
- 逻辑回归就是将线性回归的值映射到sigmod函数当中,两者的求解步骤是类似的。
3. 监督学习与无监督学习
- 监督学习的学习方法是分类和回归,常用的算法是K-近邻算法、决策树、朴素贝叶斯、逻辑回归。
- 无监督学习的学习方法是:
- 聚类:K-均值聚类、BIRCH聚类、高斯混合聚类
- 降维:主成分分析(PCA)(通过线性变换将原始数据变换为一组各维度线性无关的表示,可以用于提取数据的主要特征分量。)
-
监督学习是根据已有数据集,知道输入和输出结果之间的关系,然后根据这种已知关系训练得到一个最优模型。训练数据应该既有特征(x)又有标签(y),然后通过训练,找到特征和标签之间的联系。
-
监督学习中的数据是带有一系列标签的,在无监督学习中,需要用某种算法去训练无标签的训练集从而能够让我们找到这组数据的潜在结构。
-
监督式学习中的分类和回归:回归指利用训练数据预测输出值,例如利用回归从训练数据中预测股票价格。分类指将输出分组到某一类。例如使用分类预测数据样本的年龄。
-
监督学习中的支持向量机(SVM)
- 支持向量机(SVM)是一类按监督学习方式对数据进行二元分类的广义线性分类器,其决策边界是对学习样本求解的最大边距超平面,可以将问题化为一个求解凸二次规划的问题。
三、优化
1.梯度下降法
-
在求解损失函数的最小值时,可以通过梯度下降法来迭代求解,得到最小化的损失函数和模型参数值。
-
梯度下降的分类
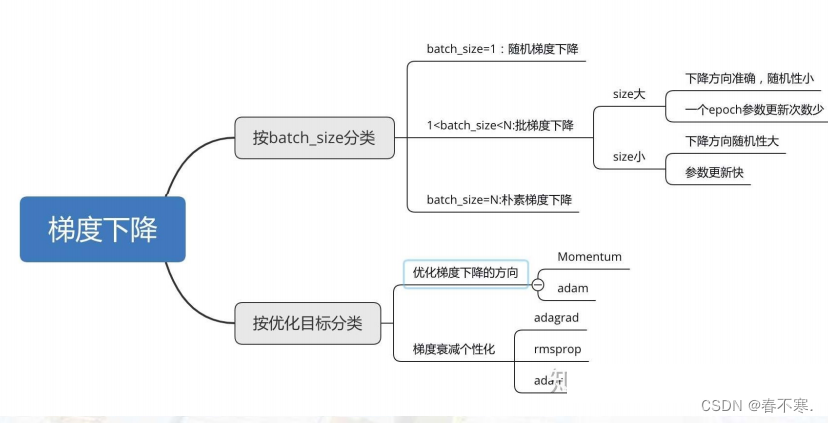
2.随机梯度下降法(SGD)
- 每次从训练集中随机选择一个样本来进行学习,Batch_size = 1
- 优点:每次只随机选择一个样本更新参数,所以学习是非常快速的,并且可以在线更新;最终收敛于一个较好的局部极值点。
- 缺点:每次更新可能不会按正确的方向进行,因此会带来优化波动,使得迭代次数增多,即收敛速度变慢。
3. 批量梯度下降法(BGD)
- 每次使用全部的训练样本来更新模型参数
- 优点:每次更新都会朝着正确的方向进行,最后能够保证收敛于极值点。
- 缺点:每次学习时间过长,并且如果训练集很大以至于需要消耗大量的内存,不能进行在线模型参数更新。
4.小批量梯度下降法(MBGD)
- 综合以上两种方法,在每次更新速度与更新次数中间的一个平衡,其每次更新从训练集中随机选择k个样本进行学习。
5.Momentum动量法
- 参数更新时在一定程度上保留之前更新的方向,同时又利用当前batch的梯度微调最终的更新方向,简言之就是通过积累之前的动量来加速当前的梯度。
- Nesterov 动量法往标准动量中添加了一个校正因子,具体做法就是在当前的梯度上添加上一时刻的动量。(更好的修正过程)
- Nesterov动量法中的β
6.优化学习率/步长
- Adagrad
- 对于经常更新的参数,我们已经积累了大量关于它的知识,不希望被单个样本影响太大,希望学习速率慢一些;对于偶尔更新的参数,我们了解的信息太少,希望能从每个偶然出现的样本身上多学一些,即学习速率大一些。(梯度平缓时加大步长)
- rmsprop
- rmsprop算法修改了AdaGrad的梯度平方和累加为指数加权的移动平均,使得其在非凸设定下效果更好。
7.反向传播算法
- BP算法的学习过程由正向传播过程和反向传播过程组成。
四、卷积神经网络
1.感受野
-
就是指输出feature map上某个元素受输入图像上影响的区域。
-
内核(kernel)是滤波器(filter)的基本元素,多张kernel组成一个filter。
-
输入通道是3个特征时,则每一个filter中包含3张kernel。
2.下采样(池化)
-
作用:保留主要特征的同时减少参数和计算量,防止过拟合,提高模型的泛化能力。
-
最大池化和平均池化:保留像素值最大或取平均。
3.Flattening平整化
- Flatten层:把多维的输入一维化,常用在从卷积层到全连接层的过渡。
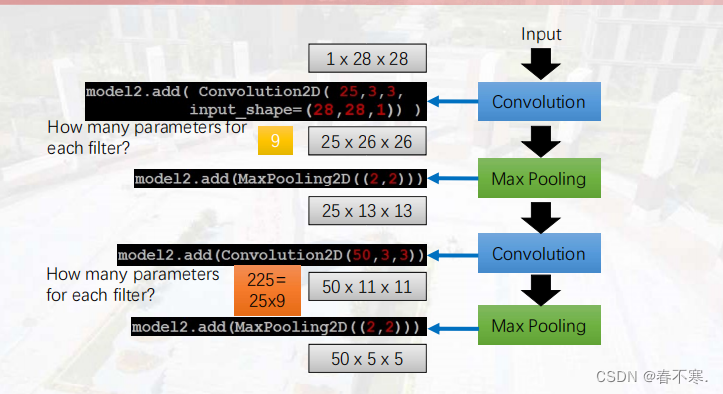
4.举例
- AlexNet使用ReLU激活函数
- LetNet5使用sigmod激活函数

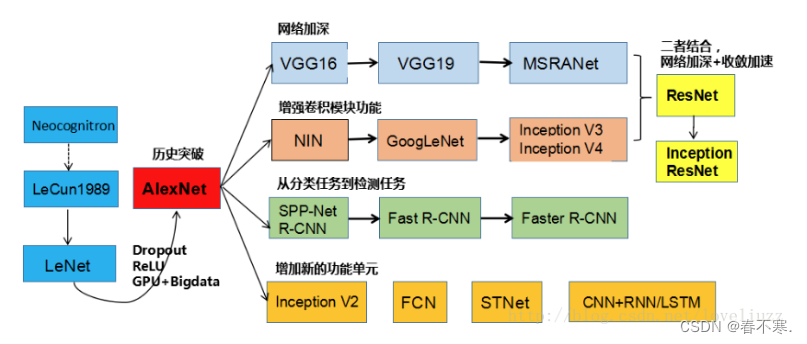
博客来源:https://blog.csdn.net/wait_ButterFly/article/details/81872706
五、循环神经网络
1. RNN的基本概念
- 他们都只能单独的取处理一个个的输入,前一个输入和后一个输入是完全没有关系的。但是,某些任务需要能够更好的处理序列的信息,即前面的输入和后面的输入是有关系的。
2.LSTM长短期记忆网络
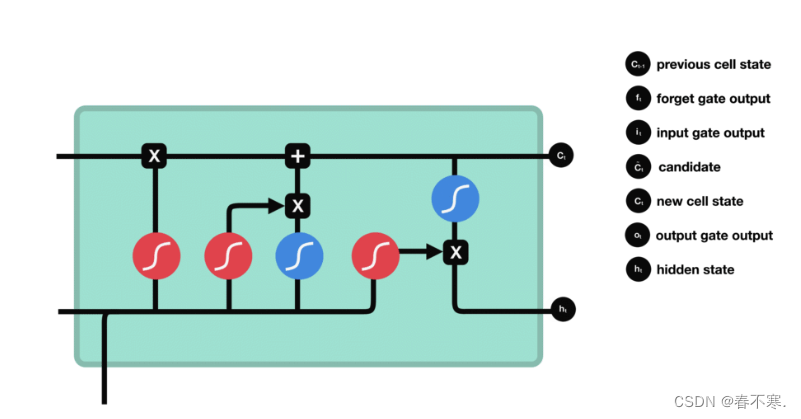
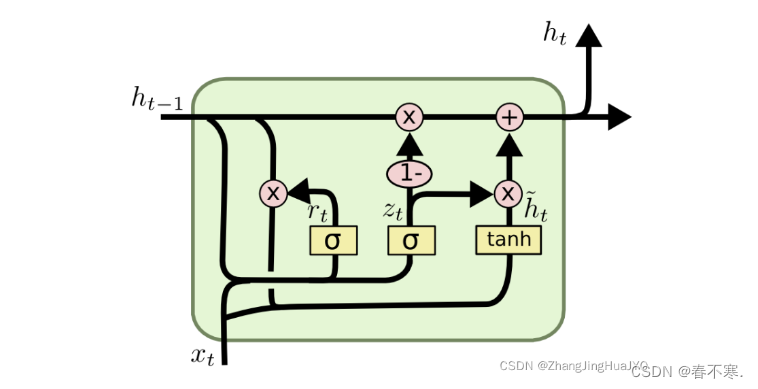
3.GRU
- 为了解决长期记忆和反向传播中的梯度等问题而提出来的
4.Attention注意力机制
- Attention机制就是对输入的每个元素考虑不同的权重参数,从而更加关注与输入的元素相似的部分,而抑制其它无用的信息。
5.Transformer模型
- 相比 RNN 网络结构,其最大的优点是可以并行计算。
- Self-Attention(自注意力),也称为Intra-Attention(内部注意力),是关联单个序列的不同位置的注意力机制,以便计算序列的交互表示。
