手把手学会DFS (递归入门)
目录
算法介绍
递归实现指数型枚举
递归实现排列型枚举
递归实现组合型枚举
算法介绍
🧩DFS 即 Depth First Search ,中文又叫深度优先搜索,是一种沿着树的深度对其进行遍历,直到尽头之后再进行回溯,再走其他路线的方法,在对数据进行枚举,或求子串数量时具有奇效。该算法的实现取决于递归,因此如何设置递归的结束条件,以及什么时候调用递归便显得十分重要。
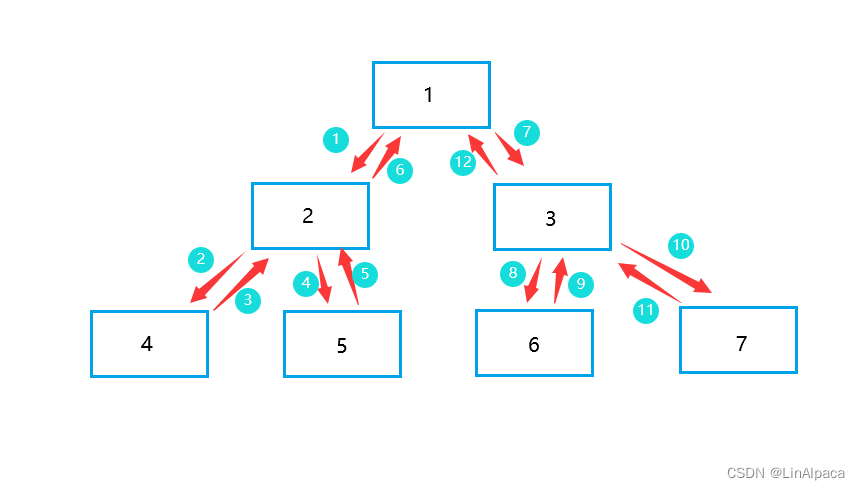
🧩通过 DFS 进行遍历,便可以无遗漏地走遍整个树,再根据题目要求在特定的位置对数据进行处理或输出。
🧩最重要的一点便是,当我们一条路走到底之后,就要回溯,就像上图中 3 5 6 步那样回到上一个节点。之后会判断是走另外一条路还是再回溯到上一层,由于在回溯前我们就已经对数据进行了处理,所以要对数据进行还原,即回溯到第一次到达这个节点时的那份数据。具体的细节就留到题目里面讲吧。
递归实现指数型枚举
传送门:AcWing 92. 递归实现指数型枚举
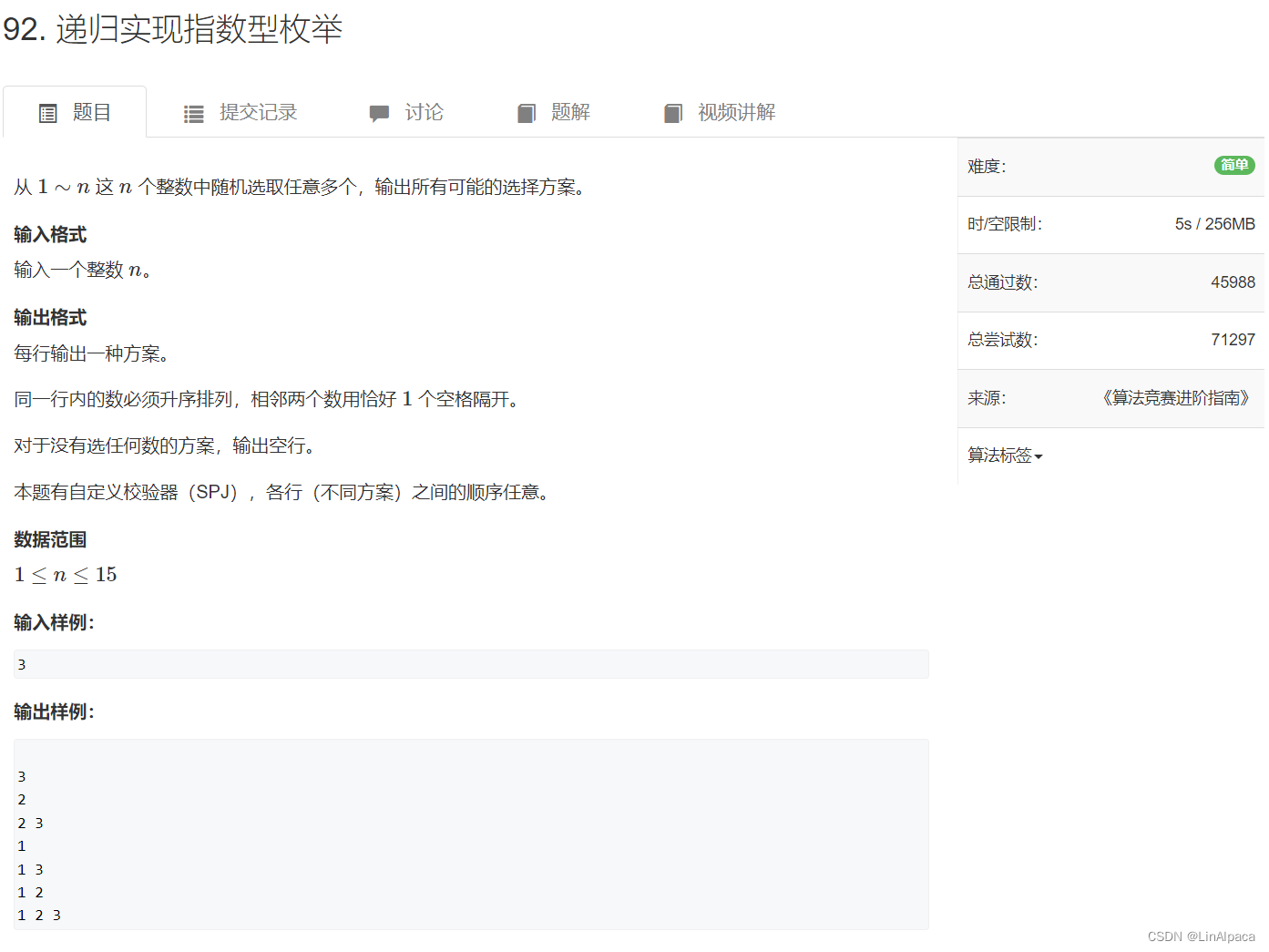
🧩DFS 的入门题,要求在 1~n 之间找所有可能出现的子序列的情况。可以全选也可以全部都不选,但输出的方式就比较宽松不需要特别处理。
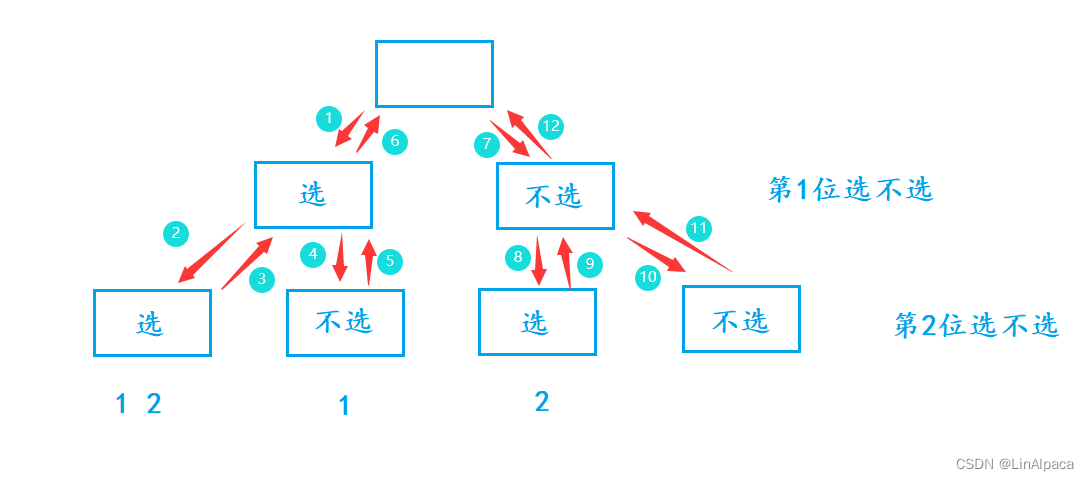
🧩于是我们就可以将 1~n 的每一位都看作有两个选择,选和不选,用一个数组存储。每次到达叶节点的时候便完成一次枚举,并输出。而每次递归参数就加一,表示往下一层,位数的增加。注意的细节都写在代码里了,结合代码进行理解。
如果比较难想象一定要画递归图!!!!
#include<cstdio>
#include<string>
#include<iostream>
#include<algorithm>using namespace std;const int N = 15;
int n;
int sta[N]; //状态数组,表示当前位的数选或不选void dfs(int i)
{if(i == n) //位数等于n,表示所有数的状态都已确定,可以进行输出{for(int j = 1;j<=n;j++){if(sta[j] == 1){printf("%d ",j);}}puts("");return;}sta[i+1] = 1; //1表示选该数字dfs(i+1); //往下一层递归sta[i+1] = 0; //回溯后重置,但其实下面就会覆盖掉加不加没区别,只是为了好理解sta[i+1] = 2; //2表示不选dfs(i+1);sta[i+1] = 0;
}int main()
{scanf("%d",&n);dfs(0); //从第0层开始return 0;
}递归实现排列型枚举
🧩传送门:AcWing 94. 递归实现排列型枚举
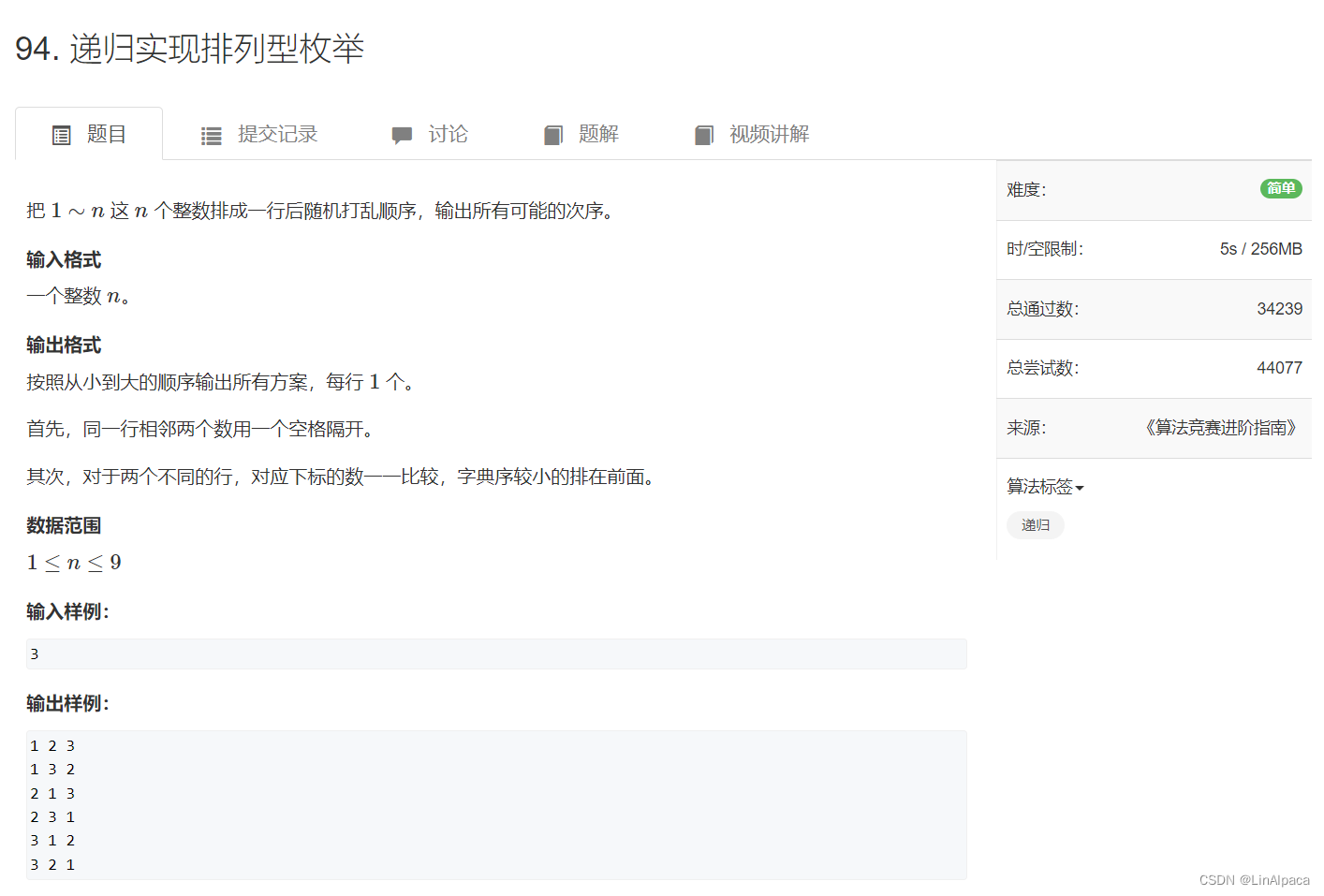
🧩依题意,一个 1~n 的整数要输出其所有的排列情况,这便于上一题不同了,上一题是每位数的相对位置都是固定的,输出长度是不固定的。但这题固定长度,但每个位的数字并不是固定的。那我们便可以从每位出发,枚举每一位可能出现的数字,但每个数字都只能出现一次。因此需要一个数组记录这个数字是否被使用过。递归结束时输出当前方案,再进行回溯。
#include<cstdio>
#include<string>
#include<iostream>
#include<algorithm>using namespace std;const int N = 10;
int n,count;
int sta[N]; //用于存储方案
bool used[N]; //有没有被用过void dfs(int i)
{if(i>n) //从1开始递归则判断条件为i>n从0开始则是i=n结束递归{for(int j = 1;j<=n;j++) printf("%d ",sta[j]); //输出puts("");return;}for(int j = 1;j<=n;j++) //寻找还没有用过的数{if(!used[j]) //true表示用过,false表示未用{sta[i] = j; //i位置选jused[j] = true; //标记j已使用dfs(i+1); //往下一位递归used[j] = false; //回溯后当前位就不使用了于是置为false}} //之后继续寻找下一个没有用过的数
}int main()
{scanf("%d",&n);dfs(1);return 0;
}递归实现组合型枚举
🧩传送门:AcWing 93. 递归实现组合型枚举
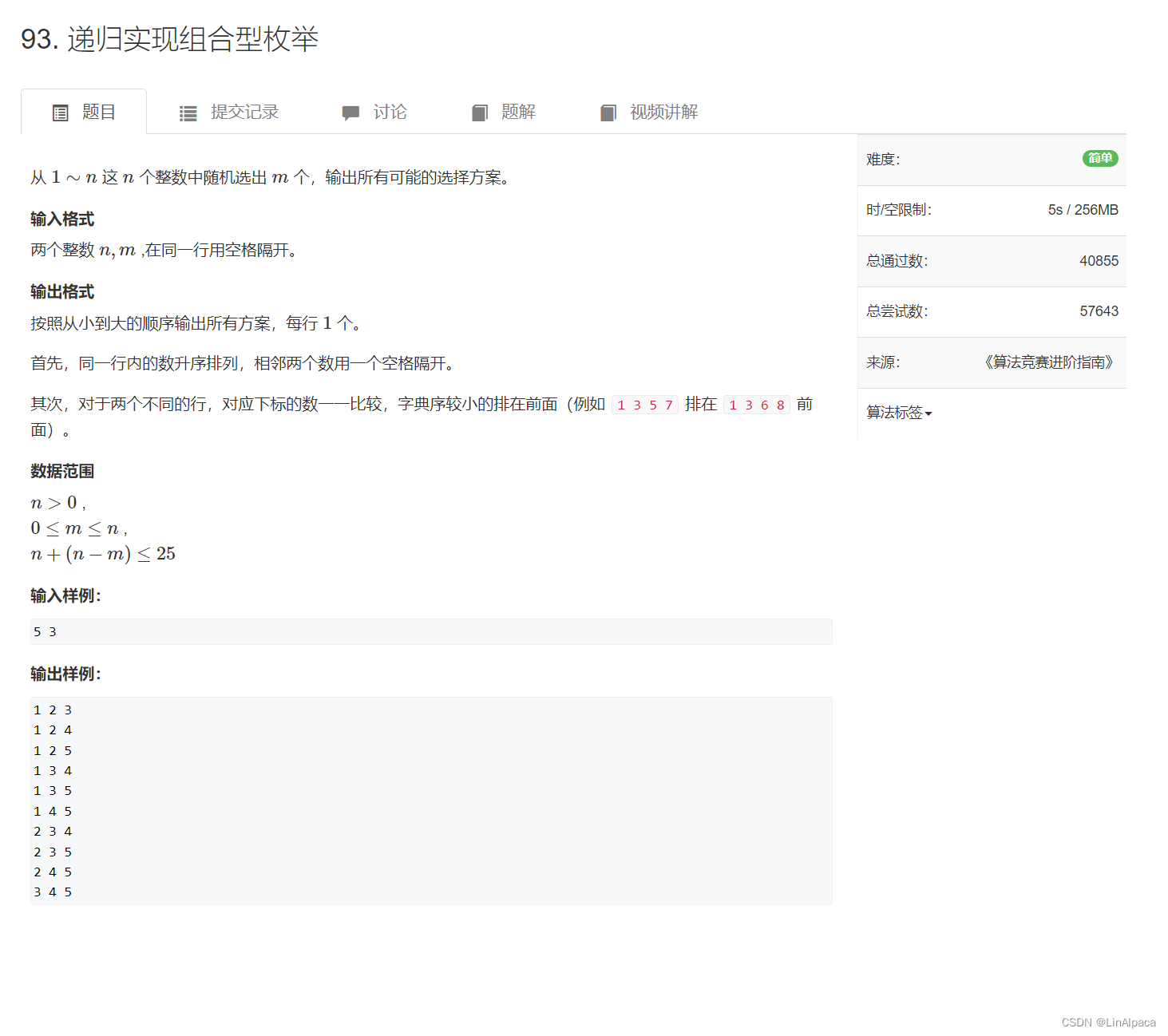
🧩这题就有点像上面两题的结合版,给定 1~n 的范围输出指定长度的从小到大的全部排列。要注意的是输出的情况是严格递增的,即不会出现中途有数字小于前面数字的情况。所以在查找没用过的数字时,需要从上一位加一开始查找。只有位数达到标准了才输出,因此会筛选掉一些不符合要求的答案。
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>using namespace std;const int N = 26;
int n, m;
int sta[N]; //用于存储方案
bool used[N]; //有没有被用过
void dfs(int x)
{if (x > m) //位数符合,可以输出{for (int i = 1; i <= m; i++){printf("%d ", sta[i]);}printf("\n");return;}for (int i = sta[x - 1] + 1; i <= n; i++) //由于输出是严格递增的由此当前位一定比上一位大{if (!used[i]) //当前数未被用则进行操作,否则跳过{sta[x] = i; //当前位置选iused[i] = true; //标记当前位置已使用dfs(x + 1); //向下递归used[i] = false; //状态回溯}} //之后继续寻找下一个没有用过的数
}int main()
{scanf("%d%d", &n, &m);dfs(1);return 0;
}🧩好了这次DFS的入门讲解到这里就结束了,如果对你有用的话还请留下你的三连加关注。算法的学习还是建立在多练习上,学会了思想还需要多多实践才能熟练地掌握。
