关于利用FFT分析时域信号幅相的思考与验证

引言
利用FFT分析/估计时域信号的幅度和相位,属于传统估计的范畴。估计的准确程度受频率分辨率的影响较大。如果被估计的目标频率等于频率分辨率的整数倍,信号的幅相估计都是最准确的。一旦目标频率不等于频率分辨率的整数倍,幅度估计值将会降低,相位估计值会偏差很大。
下面会通过一些仿真来验证。
单点频实信号估计
信号幅值:10
信号相位:45°
信号频率:100Hz
信号类型:实信号
采样率:1000Hz
采样点数:100
频率分辨率:10Hz
信号频率等于分辨率整数倍
MATLAB代码:
clc;
clearvars;
close all;fs=10e2;
f0=1e2;
p0=-pi/8;
N=100;
t=(0:N-1)/fs;
s=10*cos(2*pi*f0*t+p0);
figure;
subplot(311)
plot(s)
title('时域波形');xlabel('采样点数');ylabel('采样幅度')subplot(312)
plot((linspace(-fs/2,fs/2-fs/N,N)),abs(fftshift(fft(s)))/N)
title('幅度谱');xlabel('频率/Hz');ylabel('幅度')subplot(313)
plot((linspace(-fs/2,fs/2-fs/N,N)),angle(fftshift(fft(s)))/pi*180)
title('相位谱');xlabel('频率/Hz');ylabel('相位/°')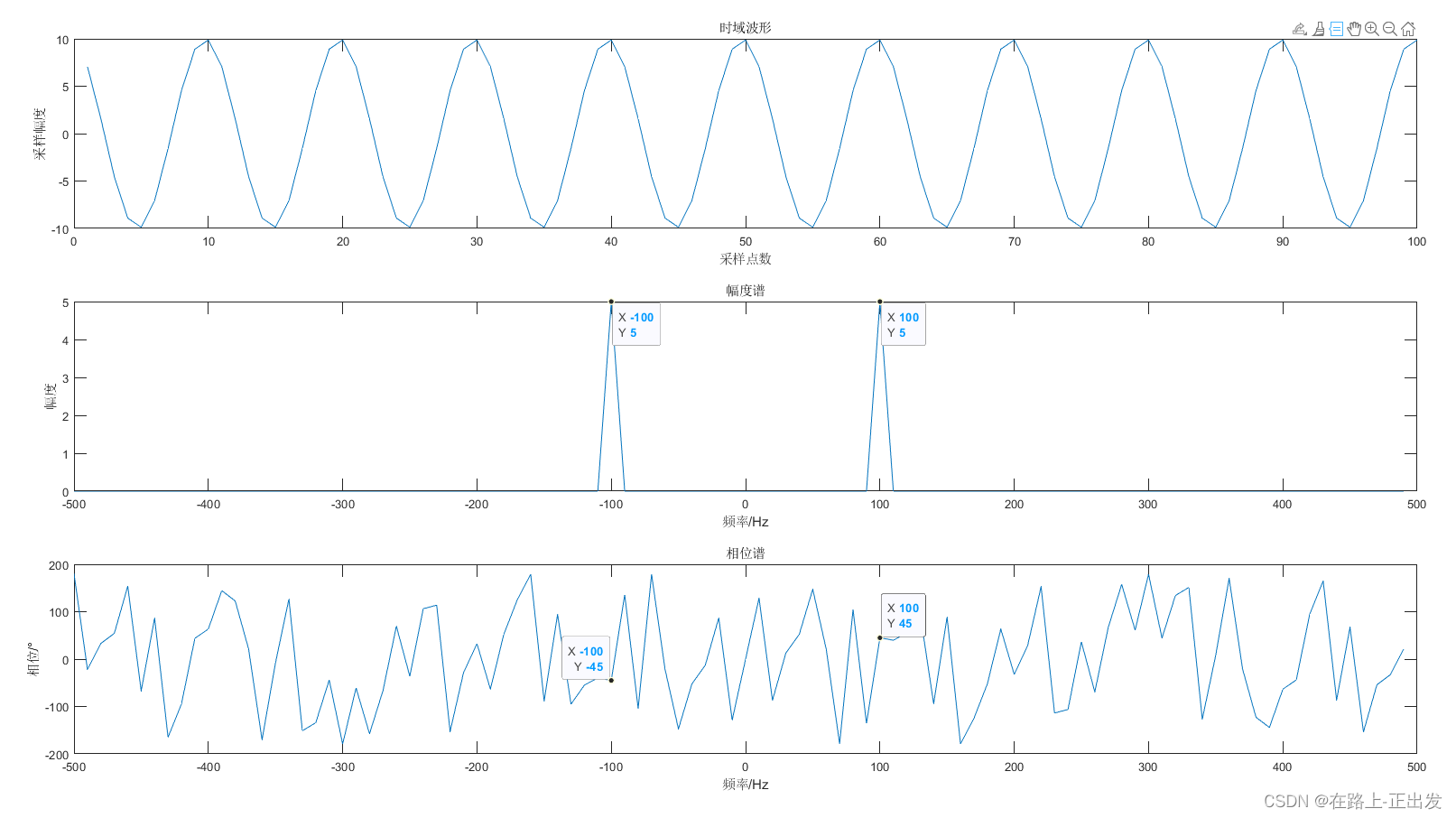
注意,此处分析的双边谱,所以每边高度为 10/2 = 5;
相位估计很准确,是45°相位。
信号频率不等于分辨率整数倍
如果改变采样点数(改为128),使得频率分辨率变化,不等于分辨率的整数倍,则:
clc;
clearvars;
close all;fs=10e2;
f0=1e2;
p0=pi/4;
N=128;
t=(0:N-1)/fs;
s=10*cos(2*pi*f0*t+p0);
figure;
subplot(311)
plot(s)
title('时域波形');xlabel('采样点数');ylabel('采样幅度')subplot(312)
plot((linspace(-fs/2,fs/2-fs/N,N)),abs(fftshift(fft(s)))/N)
title('幅度谱');xlabel('频率/Hz');ylabel('幅度')subplot(313)
plot((linspace(-fs/2,fs/2-fs/N,N)),angle(fftshift(fft(s)))/pi*180)
title('相位谱');xlabel('频率/Hz');ylabel('相位/°')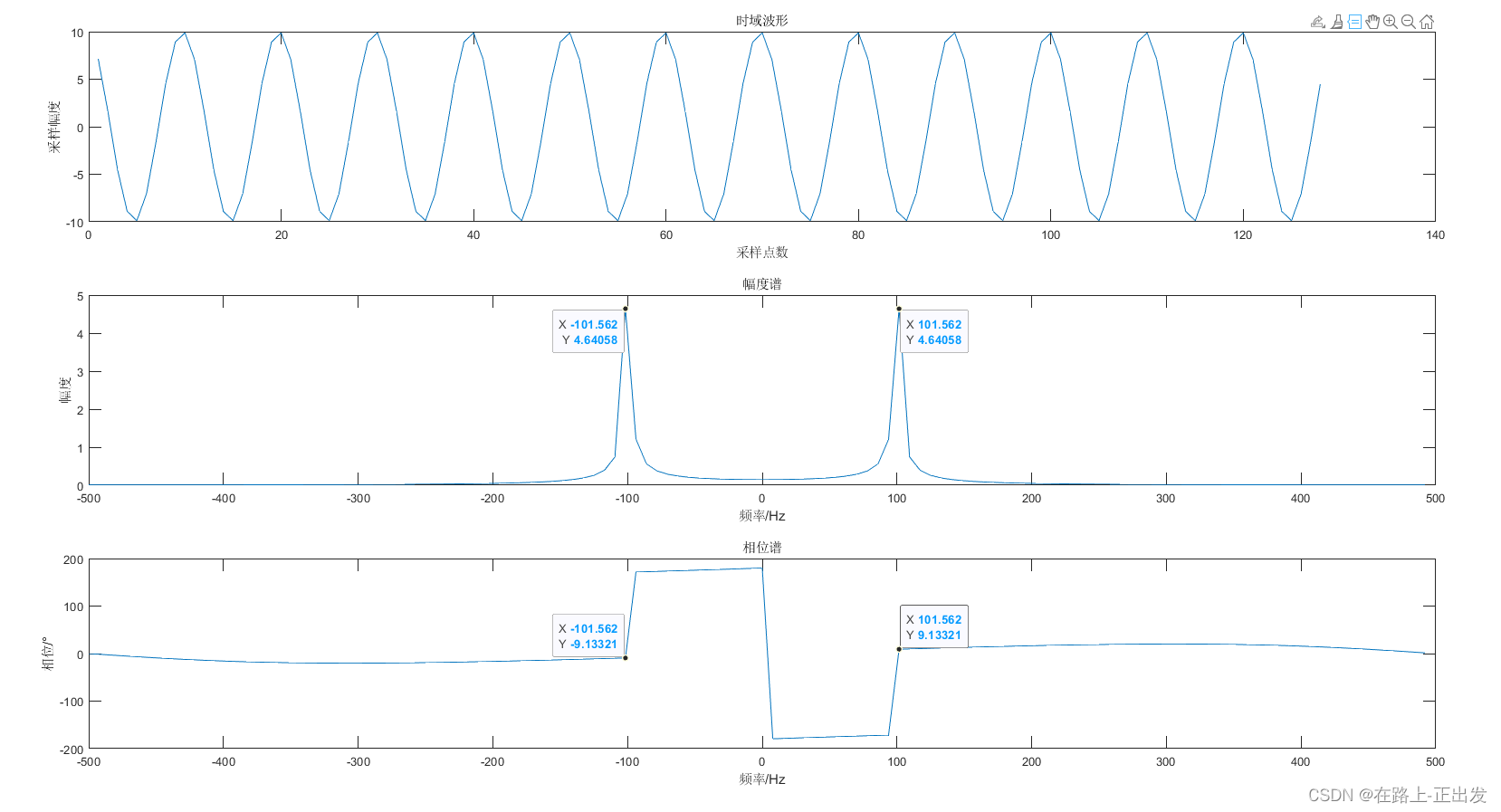
根据仿真结果,发现频率、幅度估值有微小偏差,相位的估计值几乎不可信。
信号频率等于分辨率整数倍,加噪声
考虑噪声影响:
clc;
clearvars;
close all;fs=10e2;
f0=1e2;
p0=pi/4;
N=100;
t=(0:N-1)/fs;
s=10*cos(2*pi*f0*t+p0) + 2*randn(1,N);
figure;
subplot(311)
plot(s)
title('时域波形');xlabel('采样点数');ylabel('采样幅度')subplot(312)
plot((linspace(-fs/2,fs/2-fs/N,N)),abs(fftshift(fft(s)))/N)
title('幅度谱');xlabel('频率/Hz');ylabel('幅度')subplot(313)
plot((linspace(-fs/2,fs/2-fs/N,N)),angle(fftshift(fft(s)))/pi*180)
title('相位谱');xlabel('频率/Hz');ylabel('相位/°')
根据仿真结果,信号的频率估计准确,但是幅度和相位的估计存在微小误差。
多点频实信号估计
信号的频点均位于频率分辨率整数倍的位置:
clc;
clearvars;
close all;fs=10e2;
f0=1e2;
p0=pi/4;
f1=2e2;
p1=pi/2;
N=100;
t=(0:N-1)/fs;
s=10*cos(2*pi*f0*t+p0) + 4*cos(2*pi*f1*t+p1);
figure;
subplot(311)
plot(s)
title('时域波形');xlabel('采样点数');ylabel('采样幅度')subplot(312)
plot((linspace(-fs/2,fs/2-fs/N,N)),abs(fftshift(fft(s)))/N)
title('幅度谱');xlabel('频率/Hz');ylabel('幅度')subplot(313)
plot((linspace(-fs/2,fs/2-fs/N,N)),angle(fftshift(fft(s)))/pi*180)
title('相位谱');xlabel('频率/Hz');ylabel('相位/°')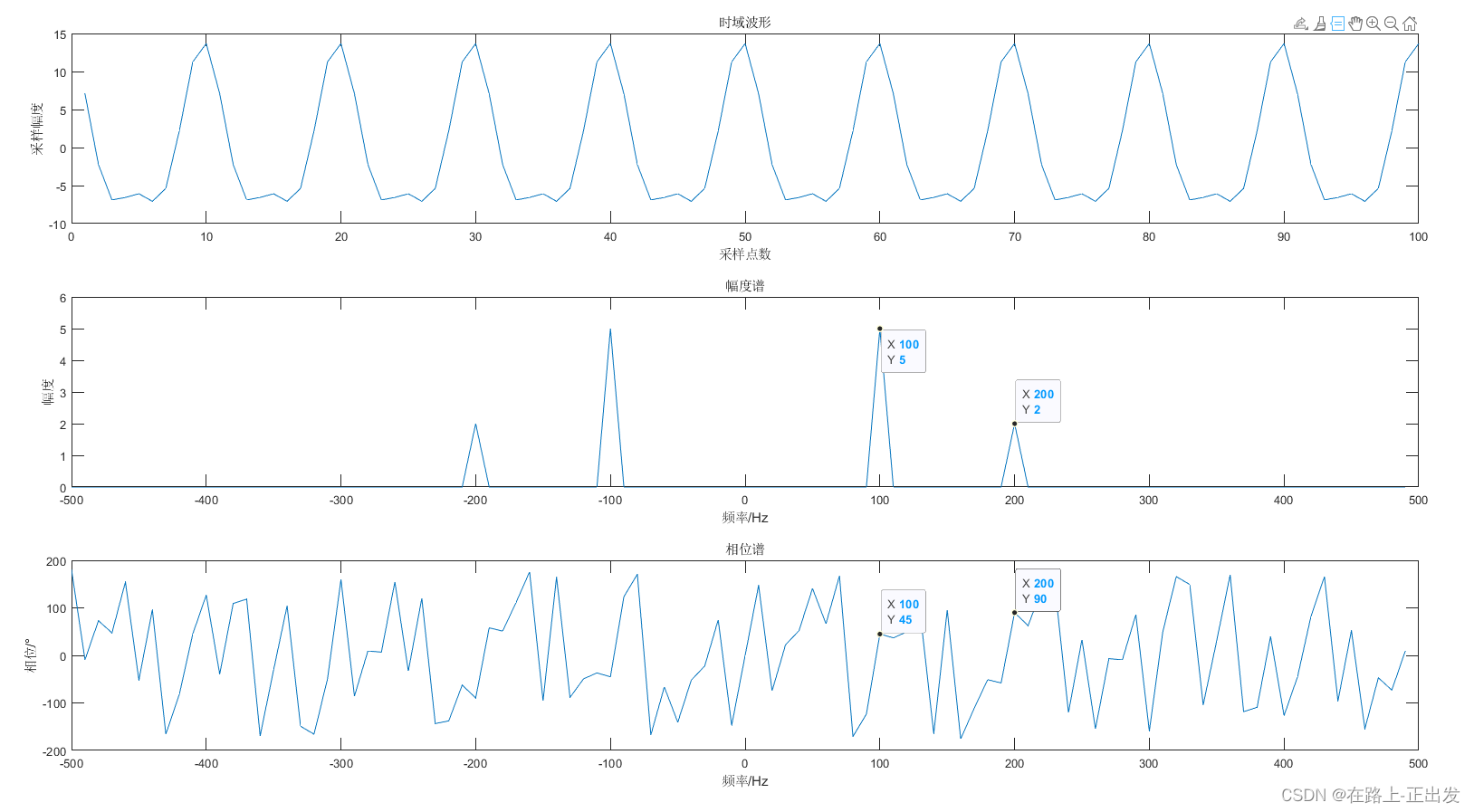
对于多点频信号,只要信号频点均位于分辨率整数倍的位置,其估值都十分准确。
多点频复信号估计
下面再试验一下复信号:
clc;
clearvars;
close all;fs=10e2;
f0=1e2;
p0=pi/4;
f1=2e2;
p1=pi/2;
N=100;
t=(0:N-1)/fs;
s=10*exp(1j*(2*pi*f0*t+p0)) + 4*exp(1j*(2*pi*f1*t+p1));
figure;
subplot(411)
plot(real(s))
title('时域波形(实部)');xlabel('采样点数');ylabel('采样幅度')subplot(412)
plot(imag(s))
title('时域波形(虚部)');xlabel('采样点数');ylabel('采样幅度')subplot(413)
plot((linspace(-fs/2,fs/2-fs/N,N)),abs(fftshift(fft(s)))/N)
title('幅度谱');xlabel('频率/Hz');ylabel('幅度')subplot(414)
plot((linspace(-fs/2,fs/2-fs/N,N)),angle(fftshift(fft(s)))/pi*180)
title('相位谱');xlabel('频率/Hz');ylabel('相位/°')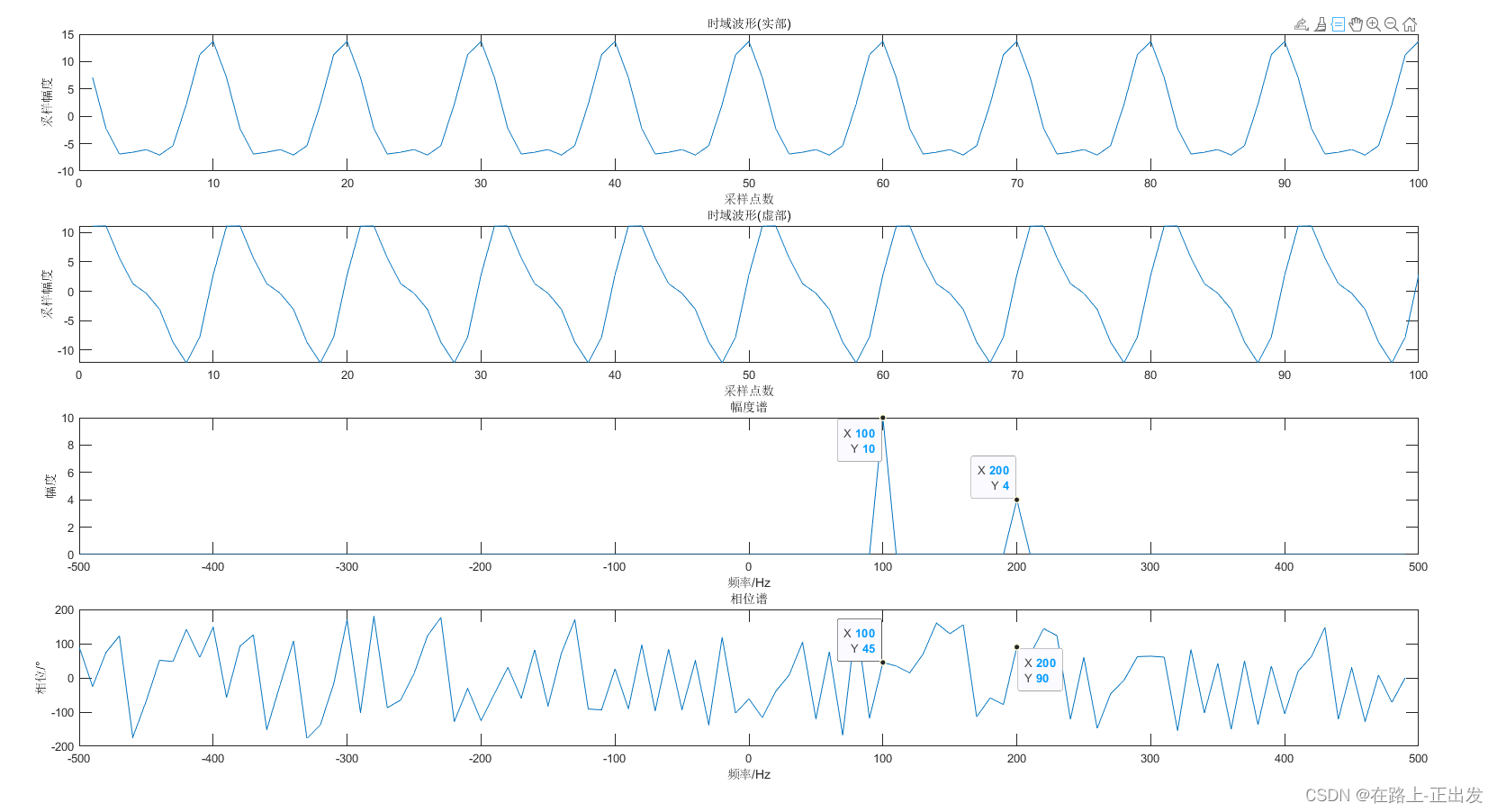
根据仿真结果,可以看出,复信号同样满足上述结论,即信号频率位于分辨率整数倍位置时,用FFT可以精确估计其频率和相位。
结论
结尾处再次说明一下:
不论是是信号还是复信号:
- 不加噪声时,位于分辨率整数倍处的信号频率、相位均可以被精确估算;
- 不加噪声时,不位于分辨率整数倍处的信号频率的估计存在微小误差、相位估计值基本不可信;
- 加噪声时,位于分辨率整数倍处的信号频率可以被精确估算,相位估算存在微小偏差;
可以结合代码和仿真进行理解,如有疑问,评论区留言吧~~
