---

插入排序概念

直接插入排序是从一个有序的序列中选择一个合适的位置进行插入，这个合适的位置取决于是要升序排序还是降序排序。

每一次进行排序之后，这段数据都是有序的。

---

提示：以下是本篇文章正文内容，下面案例可供参考

插入排序分为2种

一 .直接插入排序

直接插入排序是从一段数据中将一个数据在合适的位置插入。

案例：
一张图弄懂直接插入排序

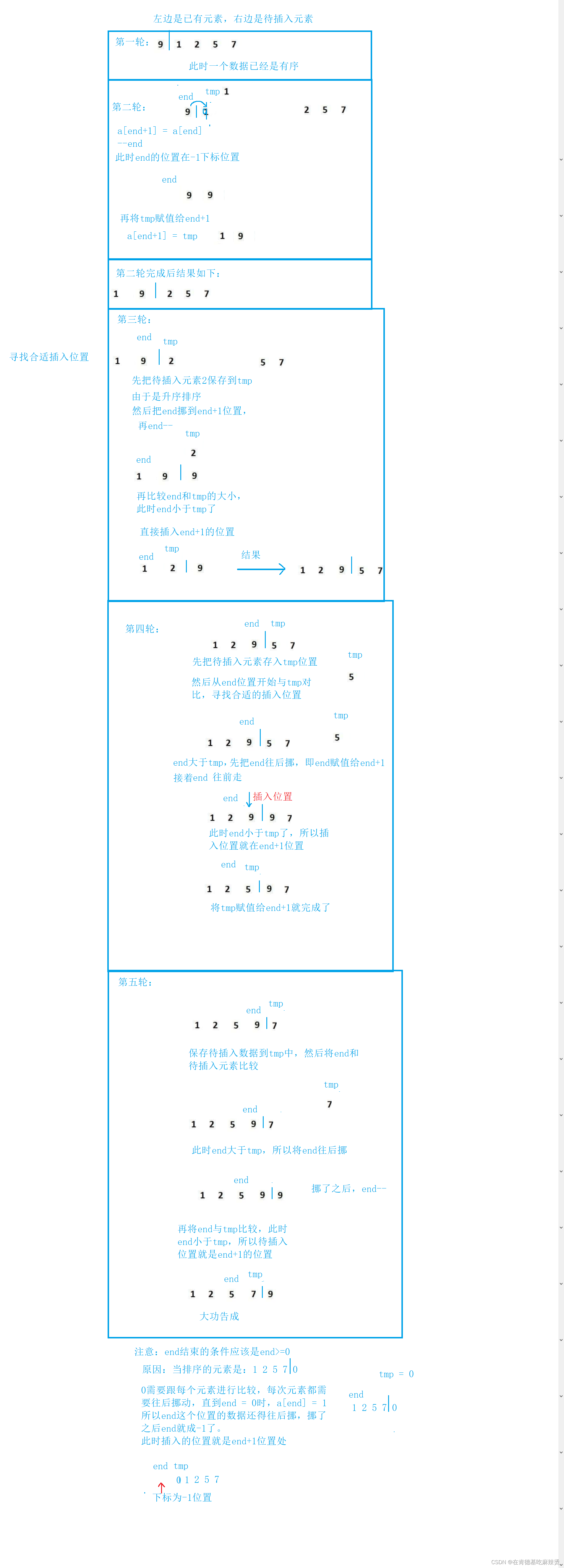
代码如下：

void InsertSort(int * a,int n )
{for(int i =0;i<n-1;i++){int end = i;//保存待插入元素int tmp = a[end+1];while(end>=0){if(a[end]>tmp){//把end往后挪a[end+1] = a[end];//end再往前走	end--;}else{break;}}//由于不管是在中间的任意地方插入还是在end的末尾插入（即tmp是最大的情况），//都是在end后面的位置插入，所以来到这里进行合并a[end+1] = tmp;}
}

直接插入排序时间复杂度

直接插入排序的时间复杂度为：O(N^2)，因为最坏的情况是逆序的情况：

每一次插入需要挪动的次数为：1+2+3+4+…+n-2+n-1 = n*n/2

所以最坏情况下的时间复杂度为O(n^2)

二.希尔排序

希尔排序可以被认为是优化后的直接插入排序。

具体优化过程如下：

给定一个gap，这个gap是把待插入的数据分成gap组，每组之间的间隔为gap长度
给定一个gap，这个gap是把待插入的数据分成gap组，每组之间的间隔为gap长度
给定一个gap，这个gap是把待插入的数据分成gap组，每组之间的间隔为gap长度

重要的事情说三遍。

比如：

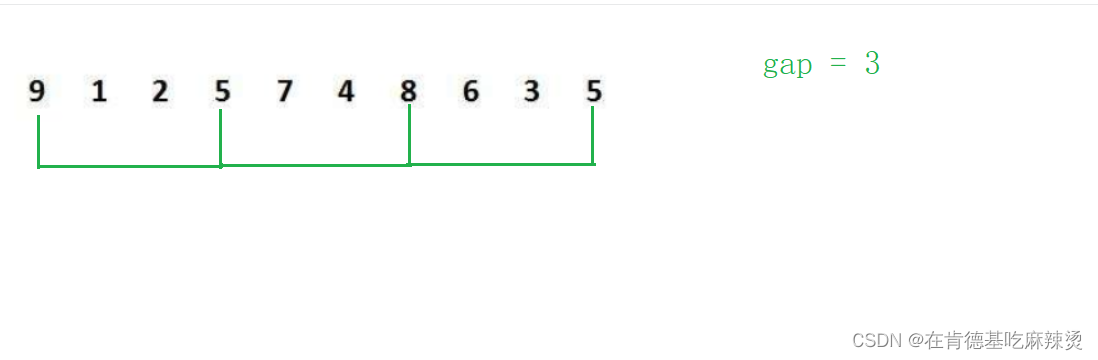
令gap = 3，即待插入的数据的间隔为3，不同于直接插入排序，直接插入排序是第一个和第二个数据的间隔永远为1，而对于希尔排序，当gap = 3时，第一个数据和第二个数据的间隔为3。
当我们把该组的元素两两比较时，大的元素就会更快地往后走。

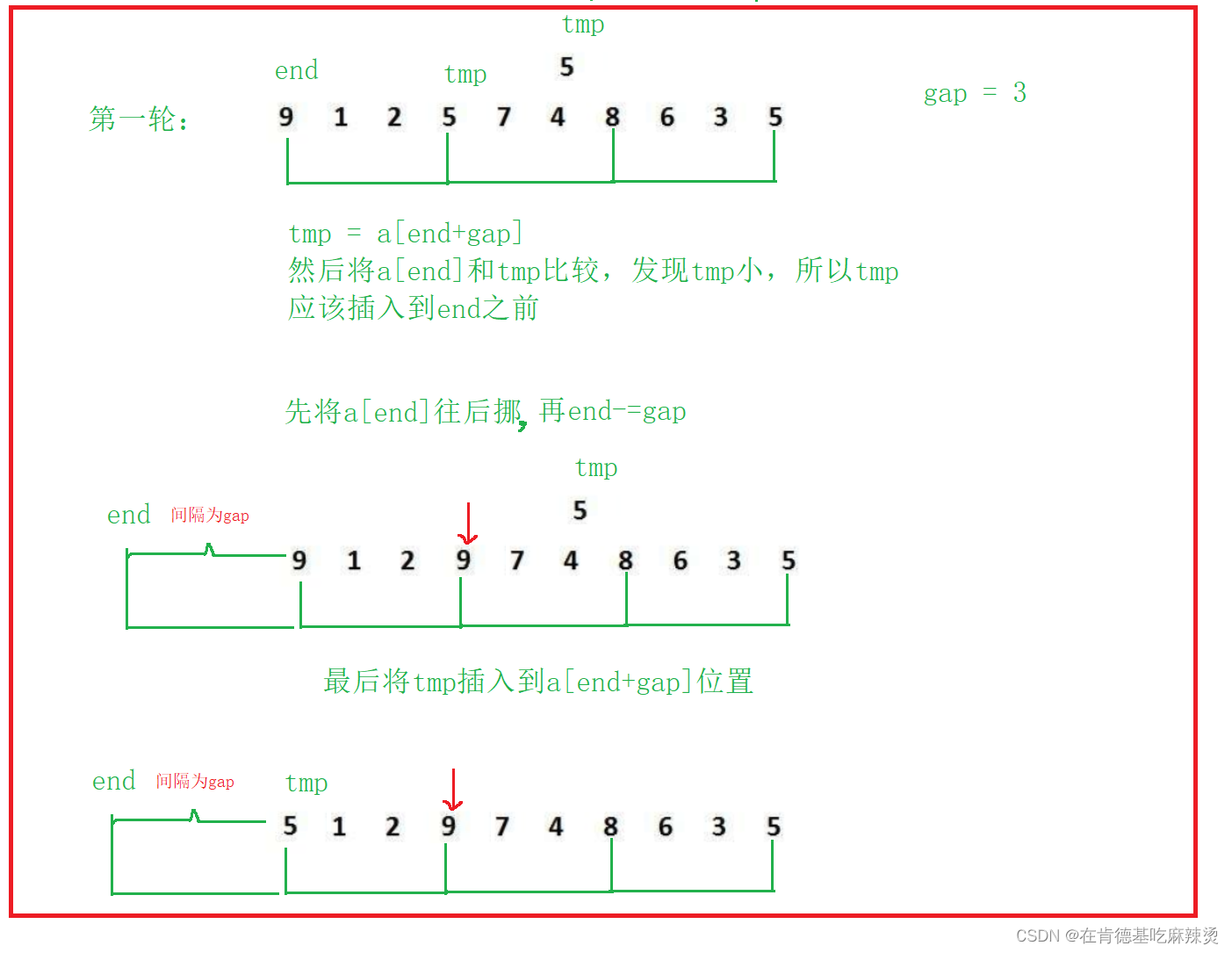
第二轮是将待插入元素8和9比较，因为9后面的第一个元素不再是7，而是9+gap的位置处的数据，即8
再将9和8进行比较，将8插入到9位置处。

当然，这是每组组内的比较，

放眼整个希尔排序来说，是多组同时进行的。

可以发现，
当gap越大，大的元素越快挪到后面
当gap越小，小的元素越慢挪到后面
当gap == 1时，就相当于上面提到的直接插入排序。

回到上面的案例，gap = 3，所以需要将数据分成3组，每组的间隔为3个长度。

如上图：此时每个元素都可以被覆盖到。

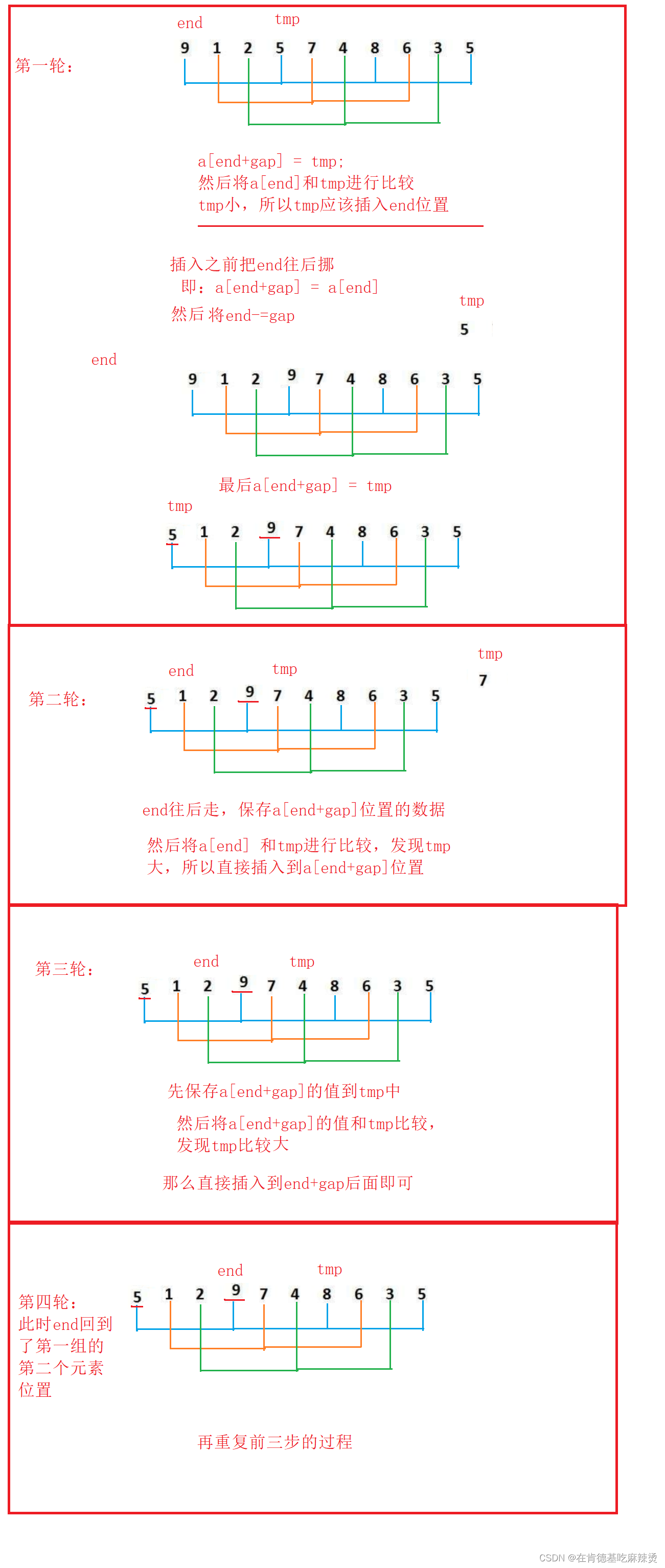
相当于同时把gap组中大的元素更快挪到后面

我们把上面的过程成为：预排序

也就是说，完成上面的操作之后，整个数据并不是有序的，而是 接近有序

比如上面的案例，完成预排序后，整组数据为：

此时是接近有序，所以此时令gap = 1，即最后接近有序的时候进行直接插入排序即可。

注意：gap的取值是不确定的：
gap取值越大，大的数据越快挪到后面，但越不接近有序
gap取值越小，大的数据越慢挪到后面，但越接近有序

总之gap是一定不能固定，并且gap的取值最后必须为1。

gap的取值应该是从大逐渐到小过渡的。

gap的取值一般是：

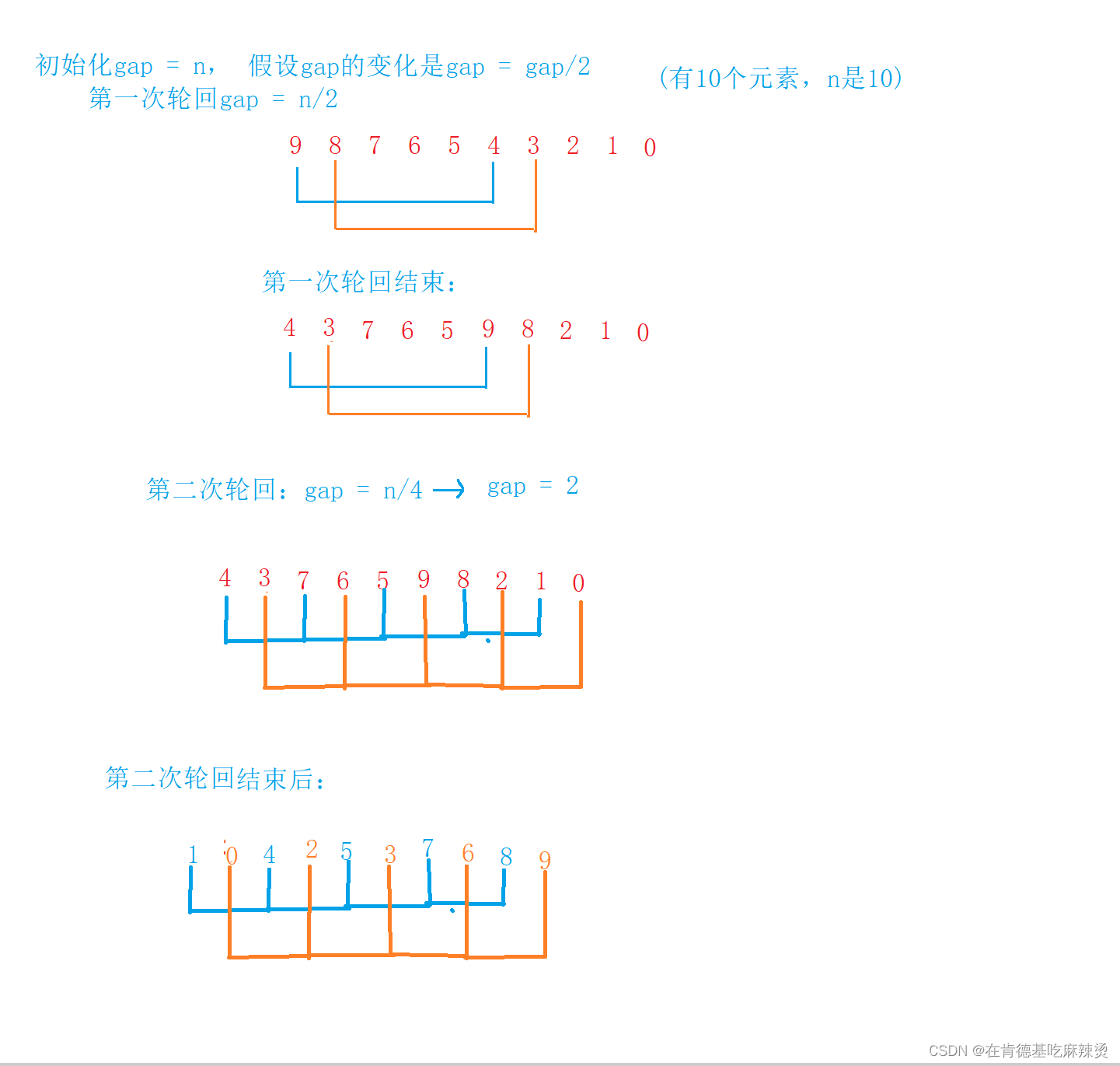
初始化gap = n，

进入轮回时：

gap = gap/3+1 或者 gap = gap/2，每次轮完一轮后，gap都会减小。

当gap的取值是gap = gap/2时，时间复杂度为：O(N*logN)，logN是以2为底N的对数

最坏情况同样为逆序：

最后一轮gap = 1，此时为直接插入排序，则N/2/2/2/…/2 = 1，
每次轮回一次gap，gap都会/2，最后一次gap = 1，则需要比较的次数是logN(以2为底N的对数)

希尔排序时间复杂度

总的时间复杂度为遍历整组元素的次数：O(N)*每次遍历进行插入的次数O(logN)
—> O(N * logN)

同理：当gap的变化是gap = gap/3-1时， 最坏情况下（逆序）每次轮回需要插入的次数是

(((N/3+1) /3+1)/3+1)… = 1
对于时间复杂度：可忽略掉+1项，所以每次轮回插入次数log3 (N) ,以3为底N的对数

总时间复杂度为O(N*log3 (N))

经过前人计算，希尔排序平均时间复杂度为：
O(N^1.3)

实现代码：

void ShellSort(int* a, int n)
{//当gap越大，大的值越快到达最后的位置,但越不接近有序//当gap越小，大的值越慢到达最后的位置，但越接近有序//当gap值越接近1，排序越接近顺序//刚gap == 1时，就是直接插入排序int gap = n;while (gap > 1){//两种方式均可，gap可以任取任何值，但是都必须保证gap最后一定为1//gap = gap / 2;gap = gap / 3 + 1;//在这里就是把间隔多组的数据同时排列for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){//小于的情况，需要挪动数据if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}//大于或者等于的情况，直接插入end后面else{break;}}//由于最终都需要插入end后面，所以在循环之外插入a[end + gap] = tmp;}}
}

总结：希尔排序是在直接插入排序的基础上引入一个gap，这个gap把数据分成了gap组，并且每组元素之间的间隔也为gap。
gap每次都会逐渐减小，并且最后gap一定为1，当gap为1时，代表完成了预排序，
最后一步进行直接插入排序。

---

效率比较

void TestOP()
{srand(time(0));const int N = 1000000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);assert(a1 && a2);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];}//计算到这个走位置的时间（ms）int begin1 = clock();InsertSort(a1, N);int end1 = clock();//末位置-初位置就是时间差int begin2 = clock();ShellSort(a2, N);int end2 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);free(a1);free(a2);
}int main()
{TestOP();return 0;
}

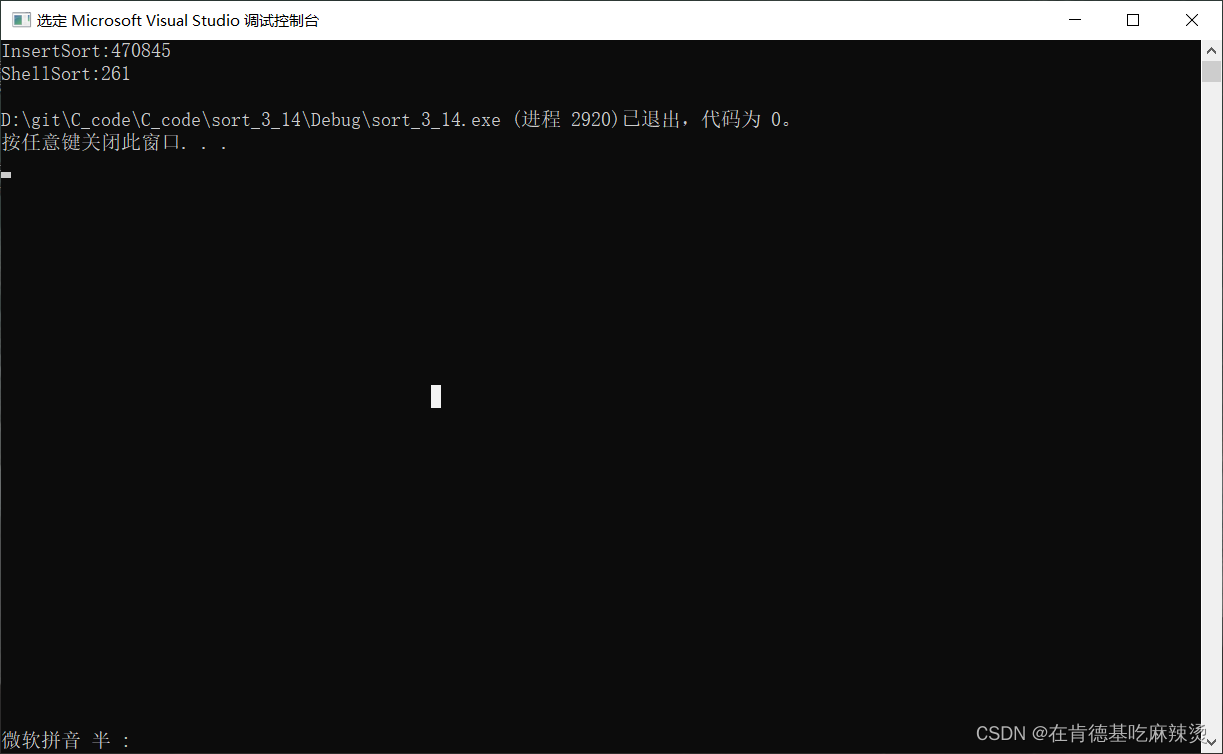
可以看到，当排序数据为100w个时，直接插入排序和希尔排序差距超过了2000倍。

直接插入排序和希尔排序的效率相比，数据越多，希尔排序较于直接插入排序的优化越大。