当前位置：首页 > news >正文

【数论】最大公约数、约数的个数与约数之和定理

news 2025/8/24 6:48:28

Halo，这里是Ppeua。平时主要更新C语言，C++，数据结构算法......感兴趣就关注我吧！你定不会失望。

🌈个人主页：主页链接

🌈算法专栏：专栏链接

我会一直往里填充内容哒！

🌈LeetCode专栏：专栏链接

目前在刷初级算法的LeetBook 。若每日一题当中有力所能及的题目，也会当天做完发出

🌈代码仓库：Gitee链接

🌈点击关注=收获更多优质内容🌈

用辗转相除法求最大公约数，以及数论相关的知识：约数个数与约数和的定理，及代码实现

题目:最大公约数

题解:

代码实现:

题目:约数个数

题解:

代码实现:

题目:约数之和

题解:

代码实现:

完结撒花：

先来科普下什么是约数：当a能被b整除，我们就说b为a的约数，b的倍数为a

题目:最大公约数

题解:

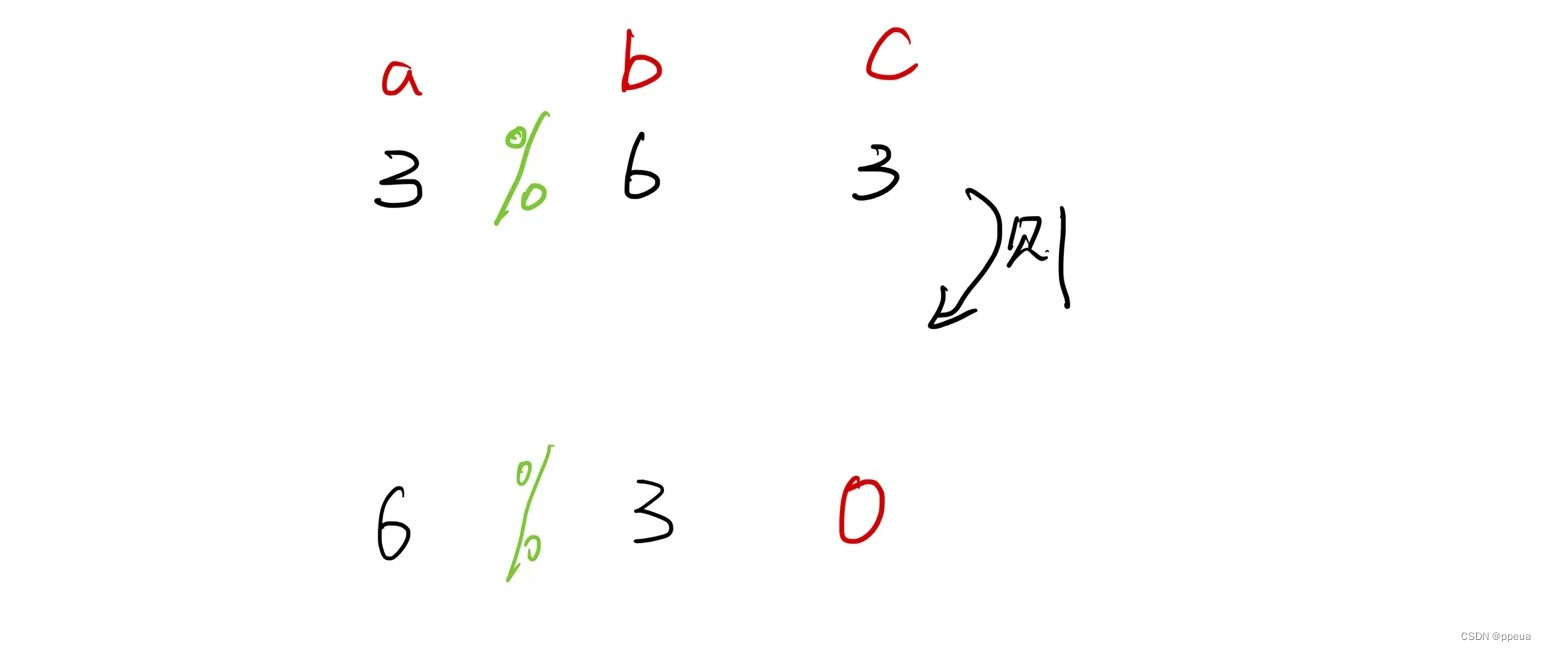
这里我们用到了辗转相除法先读入a与b这两个数，之后把a与b相除，令其结果为c，若c不为0，则令a=b，b=c（辗转就是体现在了这里），若c为0，则说明b为a的最大公约数，则输出b即可

代码实现:

#include<iostream>
using namespace std;
int gcd(int a,int b)
{return b?gcd(b,a%b):a;
}
int main()
{int n=0;cin>>n;while(n--){int a,b;cin>>a>>b;cout<<gcd(a,b)<<endl;}return 0;
}

题目:约数个数

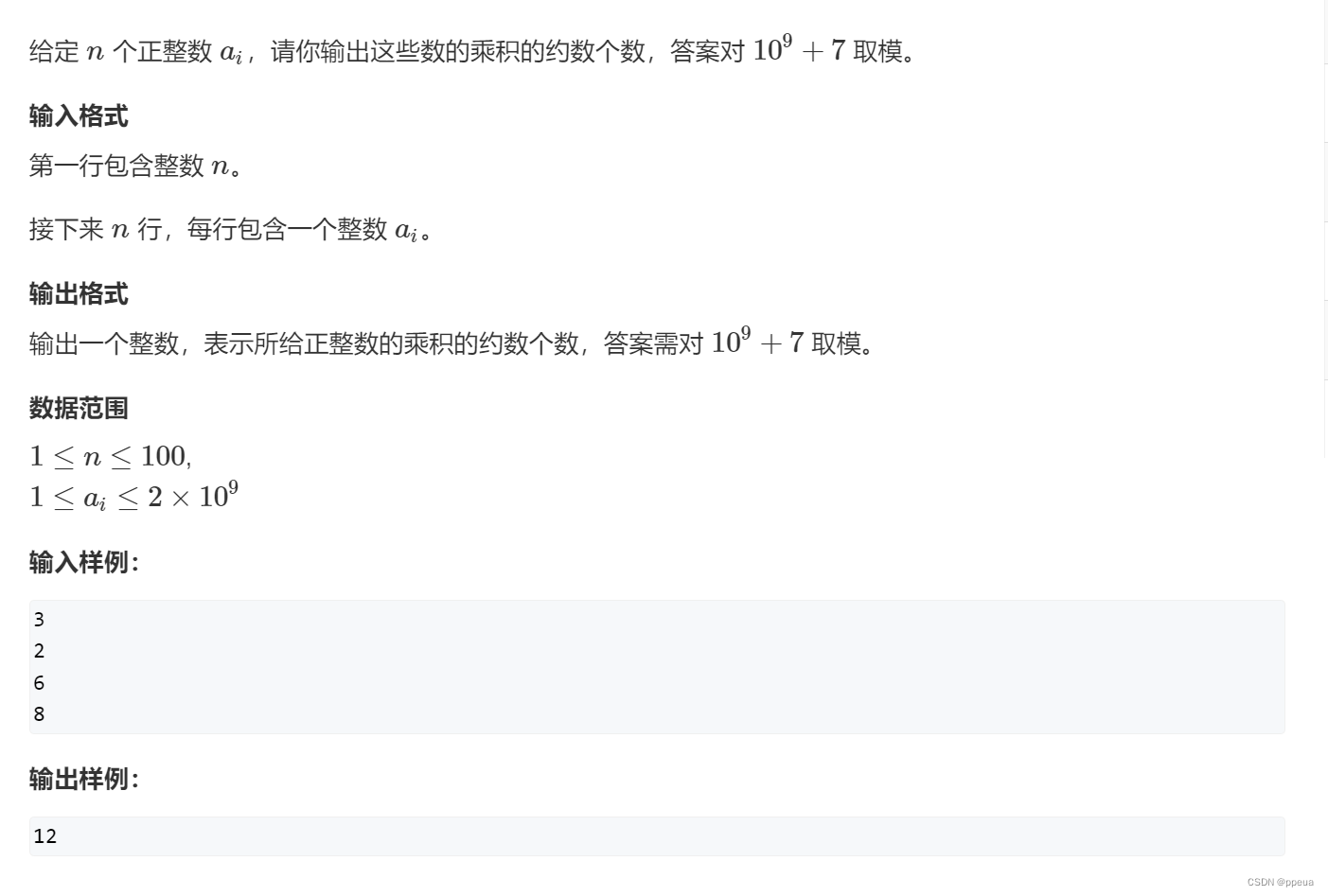
题解:

这里先科普一个数学知识，约数个数定理，假设这个数为16，求出他的质因子为2，其指数为4

那么其约数的个数就为指数加一（4+1）

可以这样理解

第一个约数为其因子的1次方2，第二个约数为其因子的二次方2*2

第三个约数为其因子的三次方2*2*2

第四个约数为其因子的四次方2*2*2*2 第五个约数为其因子的0次方也就是1

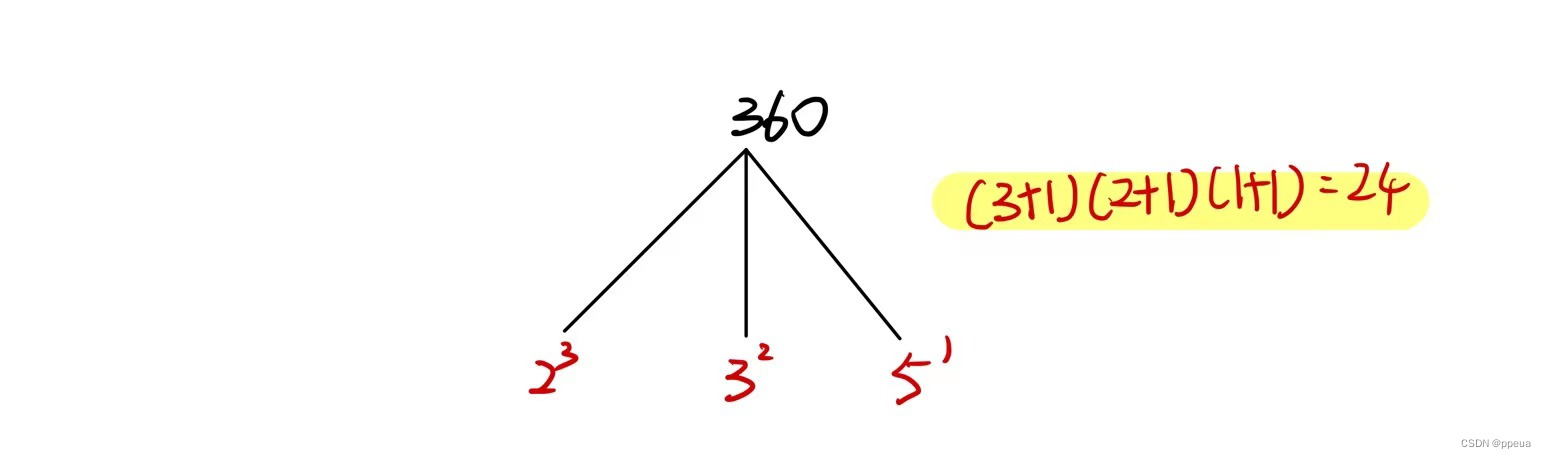
再举一个例子：

所以360的约数个数就为（3+1）*（2+1）*（1+1）

这就是约数个数定理

回顾一下我们要做的就是将一个数求出他每一个质因子（不会的uu们可以看看这篇文章分解质因数）并记录其指数情况。之后将指数拿出来做乘法就ok了

这里用hash表记录其质因子与指数的情况，其中key为质因子 value为指数，所以最后的表达式就为指数value，所以最后就将其加一再相乘即可。

代码实现:

#include<iostream>
#include<unordered_map>
using namespace std;
const int N=1e9+7;
int main()
{unordered_map<int,int>map;int n=0,s;cin>>s;while(s--){cin>>n;for(int i=2;i<=n/i;i++){while(n%i==0){n/=i;map[i]++;}}if(n>1)map[n]++;}long long res=1;for(auto ma:map){long long p=1;int a=ma.second;res=(res*(a+1))%N;}cout<<res;
}

题目:约数之和

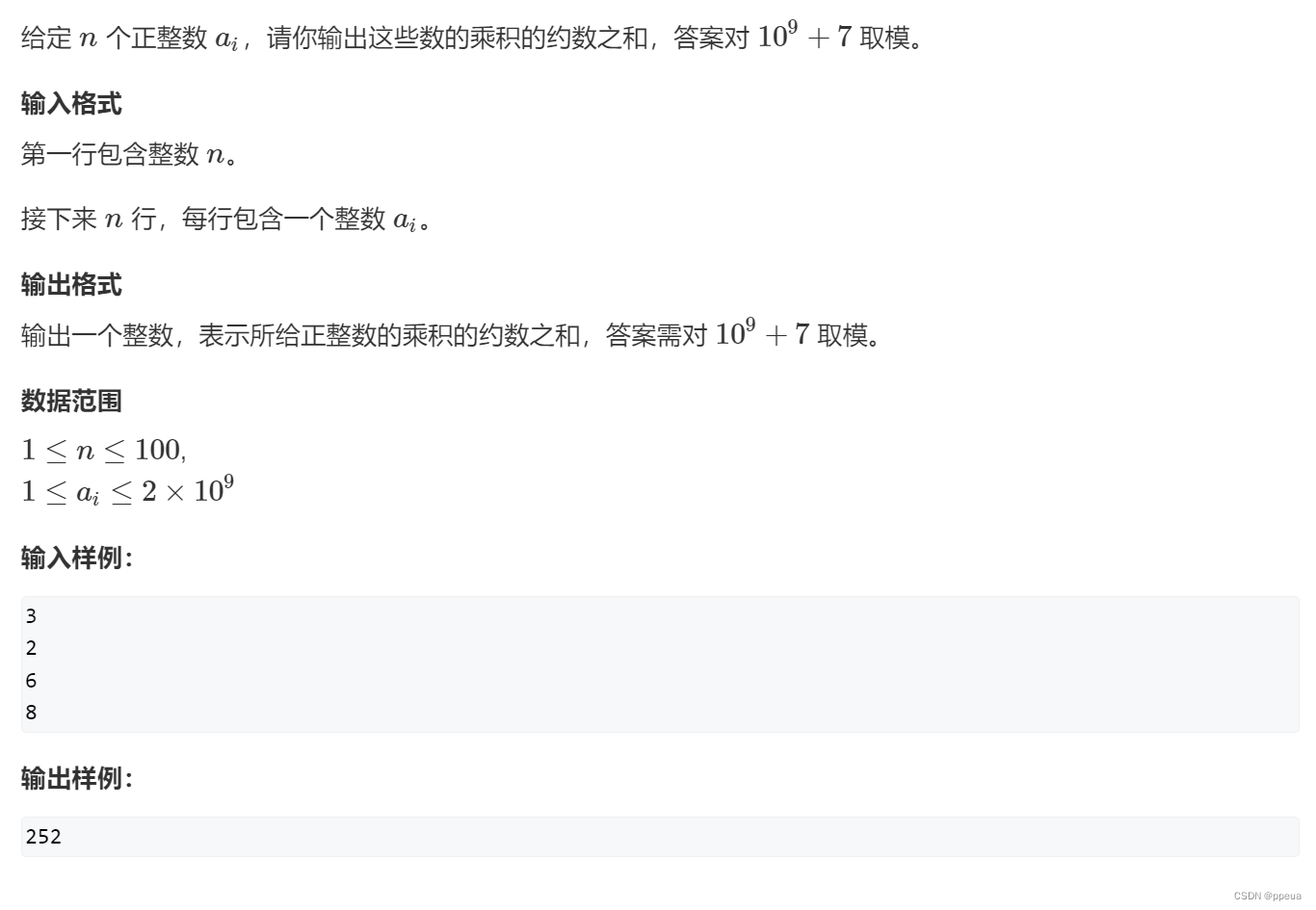
题解:

上面学了约数个数的定理，现在我们再来学一下约数之和定理，同样非常的简单

仍然以16来举例子，其质因子为2指数为4.

所以其约数之和为（2^0+2^1+2^2+2^3+2^4）=31

再来举上面360的例子：

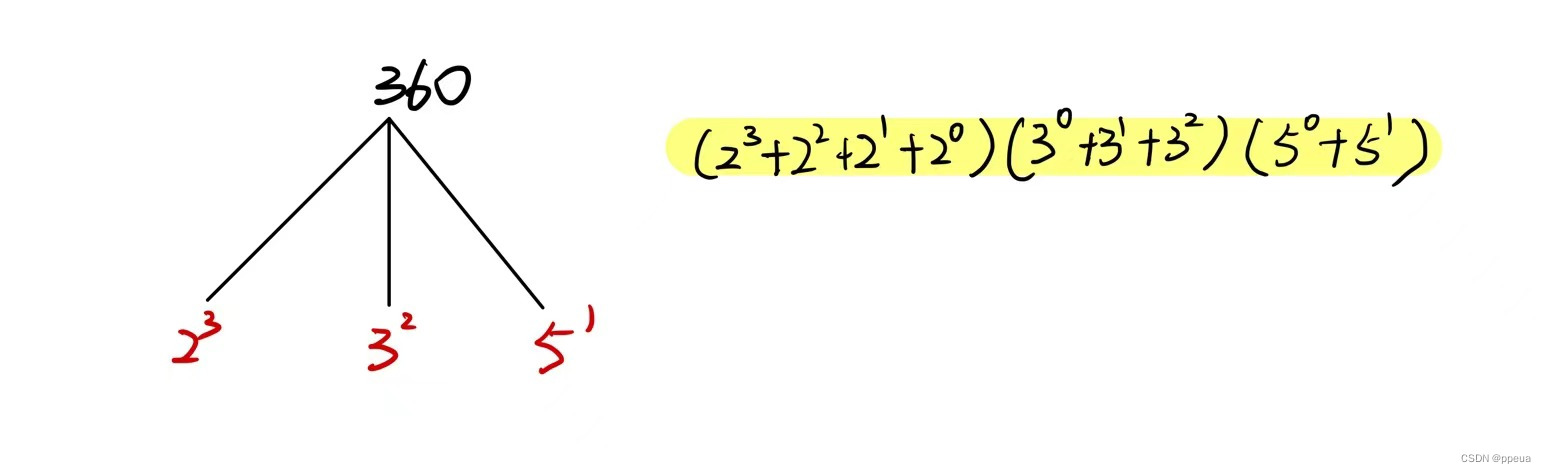
所以其约数之和为1261

这就是约数之和定理。

回顾一下我们要做的就是将一个数求出他每一个质因子（不会的uu们可以看看这篇文章分解质因数）并记录其指数情况。之后将其拿出来先相加再做乘法就ok了

这里用hash表记录其质因子与指数的情况，其中key为质因子 value为指数，所以最后的表达式就为指数value与其质因子，先相加再相乘就好。

代码实现:

#include<iostream>
#include<unordered_map>
using namespace std;
const int N=1e9+7;
int main()
{unordered_map<int,int>map;int n=0,s;cin>>s;while(s--){cin>>n;for(int i=2;i<=n/i;i++){while(n%i==0){n/=i;map[i]++;}}if(n>1)map[n]++;}long long res=1;for(auto ma:map){long long p=1;int a=ma.second;while(a--)p=(p*ma.first+1)%N;res=res*p%N;}cout<<res;
}