02.C1W1.Sentiment Analysis with Logistic Regression
目录
- Supervised ML and Sentiment Analysis
- Supervised ML (training)
- Sentiment analysis
- Vocabulary and Feature Extraction
- Vocabulary
- Feature extraction
- Sparse representations and some of their issues
- Negative and Positive Frequencies
- Feature extraction with frequencies
- Preprocessing
- Preprocessing: stop words and punctuation
- Preprocessing: Handles and URLs
- Preprocessing: Stemming and lowercasing
- Putting it all together
- General overview
- General Implementation
- Logistic Regression Overview
- Logistic Regression: Training
- 图形化
- 数学化
- Logistic Regression: Testing
- opt. Logistic Regression:Cost Function
- 作业注意事项
Supervised ML and Sentiment Analysis
Supervised ML (training)
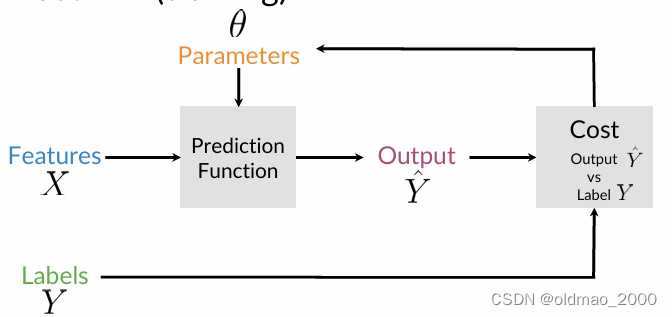
模型吃参数 θ θ θ来映射特征 X X X以输出标签 Y ^ \hat Y Y^,之前讲过太多,不重复了
Sentiment analysis
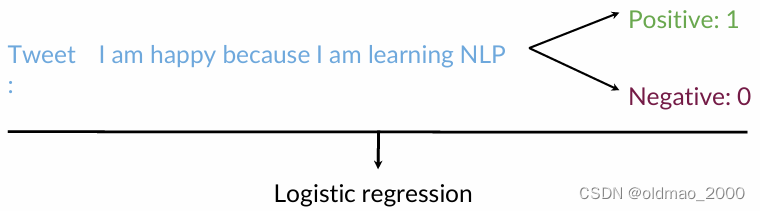
SA任务的目标是用逻辑回归分类器,预测一条推文的情绪是积极的还是消极的,如下图所示,积极情绪的推文都有一个标签:1,负面情绪的推文标签为0
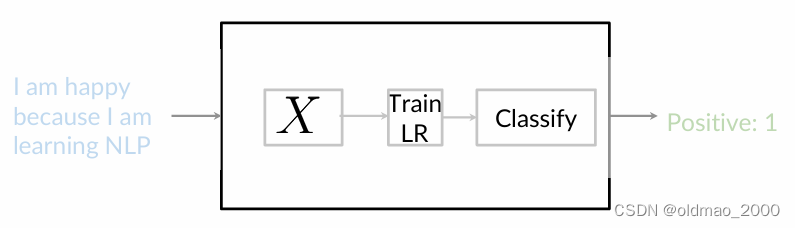
大概步骤如上图:
- 处理训练集中的原始tweets并提取有用的特征 X X X
- 训练Logistic回归分类器,同时最小化成本函数
- 使用训练好的分类器对指定推文进行情感分析预测
Vocabulary and Feature Extraction
Vocabulary
假设有训练集中有m条推文:
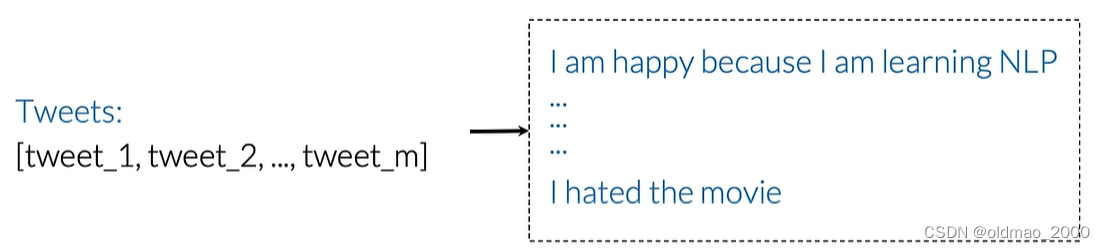
则词表(库)可表示为所有不重复出现的所有单词列表,例如上面的I出现两次,只会记录一次:

Feature extraction
这里直接简单使用单词是否出现来对某个句子进行特征提取:

如果词表大小为10W,则该句子的特征向量大小为1×10W的,单词出现在句子中,则该词的位置为1,否则为0,可以看到,句子的特征向量非常稀疏(称为稀疏表示Sparse representation)。
Sparse representations and some of their issues
稀疏表示使得参数量大,对于逻辑回归模型,需要学习的参数量为n+1,n为词表大小,进而导致以下两个问题:

Negative and Positive Frequencies
将推文语料库分为两类:正面和负面 ;
计算每个词在两个类别中出现的次数。
假设语料如下(四个句子):
| Corpus |
|---|
| I am happy because I am learning NLP |
| I am happy |
| I am sad, I am not learning NLP |
| I am sad |
对应的词表如下(八个词):
| Vocabulary |
|---|
| I |
| am |
| happy |
| because |
| learning |
| NLP |
| sad |
| not |
对语料进行分类:
| Positive tweets | Negative tweets |
|---|---|
| I am happy because I am learning NLP | I am sad, I am not learning NLP |
| I am happy | I am sad |
按类型构造词频表(小伙伴们可以自行写上对应的数字,例如:happy数字为2)


总表如下:
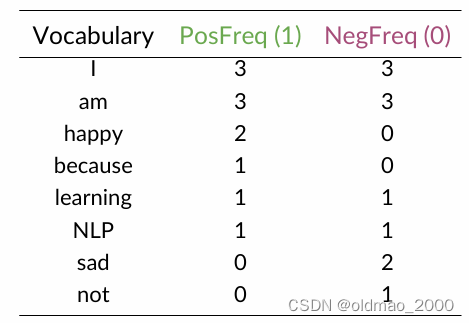
接下来就是要利用以上信息来进行特征提取。
Feature extraction with frequencies
推文的特征可由以下公式表示:
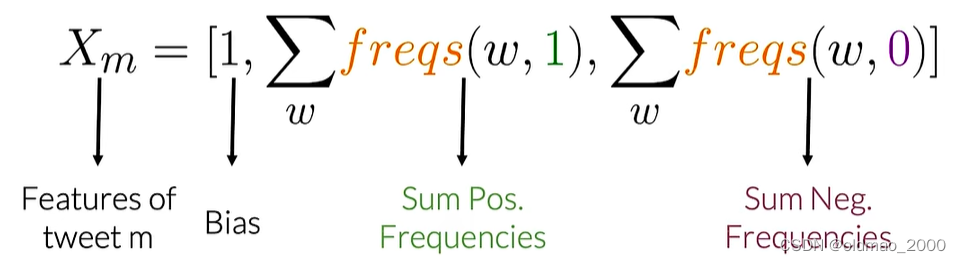
其中freqs函数就是上节表中单词与情感分类对应的频率。
例子:
I am sad, I am not learning NLP
对应正例词频表(图中应该是下划线):

可以算出正例词频总和为:3+3+1+1=8
对应负例词频表:

可以算出负例词频总和为:3+3+1+1+2+1=11
则该推文的特征可以表示为三维向量:
X m = [ 1 , 8 , 11 ] X_m=[1,8,11] Xm=[1,8,11]
这样的表示去掉了推文稀疏表示中不重要的信息。
Preprocessing
数据预处理包括:
Removing stopwords, punctuation, handles and URLs;
Stemming;
Lowercasing.
中心思想:去掉不重要和非必要信息,提高运行效率
Preprocessing: stop words and punctuation
推文实例(广告植入警告):
@YMourri and @AndrewYNg are tuning a GREAT AI model at https://deeplearning.ai!!!
假设停用词表如下(词表通常包含的停用词比实际语料中的停用词要多):
| Stop words |
|---|
| and |
| is |
| are |
| at |
| has |
| for |
| a |
交叉比较去掉停用词中的内容后:
@YMourri @AndrewYNg tuning GREAT AI model https://deeplearning.ai!!!
假设标点表如下:
| Punctuation |
|---|
| , |
| . |
| : |
| ! |
| “ |
| ‘ |
去掉标点后结果如下:
@YMourri @AndrewYNg tuning GREAT AI model https://deeplearning.ai
际这两个表可以合并在一块,当然有些任务标点符号也包含重要信息,因此是否去掉标点要根据实际需要来做。
Preprocessing: Handles and URLs
这里继续对标识符和网址进行处理,通常这些内容对于SA任务而言,并不能提供任何情绪价值。
上面的推文处理后结果如下:
tuning GREAT AI model
可以看到,去掉非必要信息后,得到结果是一条正面的推文。
Preprocessing: Stemming and lowercasing
Stemming 是一种文本处理技术,目的是将词汇还原到其基本形式,即词干。例如,将 “running” 还原为 “run”。
Lowercasing 是将所有文本转换为小写,以消除大小写带来的差异,便于统一处理。
例如第一个单词词干为tun:
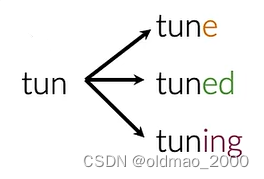
第二个单词:
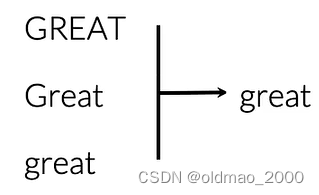
这样处理能减少词库中单词数量。最后推文处理后结果为:
[tun, great, ai, model]
Putting it all together
General overview
本节将对整组推文执行特征提取算法(Generalize the process)
根据之前的内容:数据预处理,特征提取,我们可以将下面推文进行处理:
| I am Happy Because i am learning NLP @deeplearning |
|---|
| ↓ Preprocessing后 |
| [happy, learn, nlp] |
| ↓ Feature Extraction后 |
| [1,4 ,2] |
其中,1 是Bias,4是Sum positive frequencies,2是Sum negative frequencies
对于多条推文则有:

最后的多个特征向量就可以组合成一个矩阵,大小为m×3,矩阵每一行都对应一个推文的特征向量
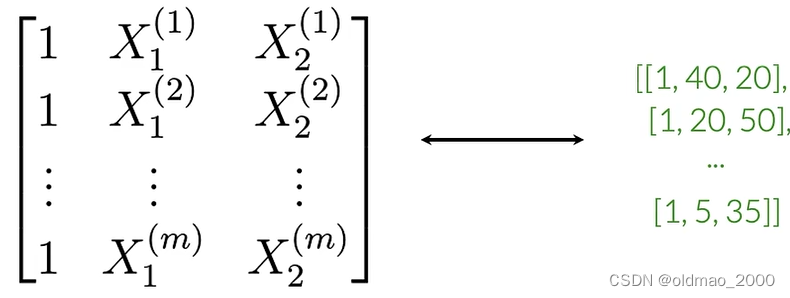
General Implementation
freqs =build_freqs(tweets,labels) #Build frequencies dictionary,已提供
X = np.zeros((m, 3 )) #Initialize matrix X
for i in range (m): #For every tweetp_tweet = process_tweet(tweets[i]) #Process tweet,已提供X[i, :]= extract_features(train_x[i], freqs)#需要在作业中自己实现
Logistic Regression Overview
最开始的有监督的机器学习中,回顾了主要步骤,这里我们只需要将中间的预测函数替换为逻辑回归函数Sigmoid即可。

Sigmoid函数形式为:
h ( x ( i ) , θ ) = 1 1 + e − θ T x ( i ) h(x^{(i)},\theta)=\cfrac{1}{1+e^{-\theta^Tx^{(i)}}} h(x(i),θ)=1+e−θTx(i)1
i为第i条数据
θ是参数
x是数据对应的特征向量
图像形式为:
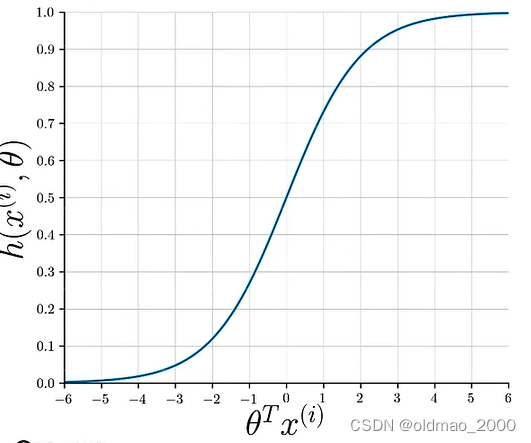
其函数值取决于 θ T x ( i ) \theta^Tx^{(i)} θTx(i):
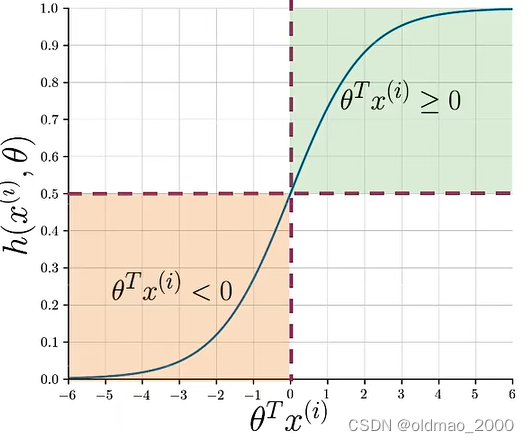
例如:
@YMourri and @AndrewYNg are tuning a GREAT AI model
预处理后结果为:
[tun, ai, great, model]
根据词库进行特征提取后可能得到以下结果:
x ( i ) = [ 1 3476 245 ] and θ = [ 0.00003 0.00150 − 0.00120 ] \begin{equation*} x^{(i)} = \begin{bmatrix} 1 \\ 3476 \\ 245 \end{bmatrix} \quad \text{and} \quad \theta = \begin{bmatrix} 0.00003 \\ 0.00150 \\ -0.00120 \end{bmatrix} \end{equation*} x(i)= 13476245 andθ= 0.000030.00150−0.00120
带入sigmoid函数后得到:
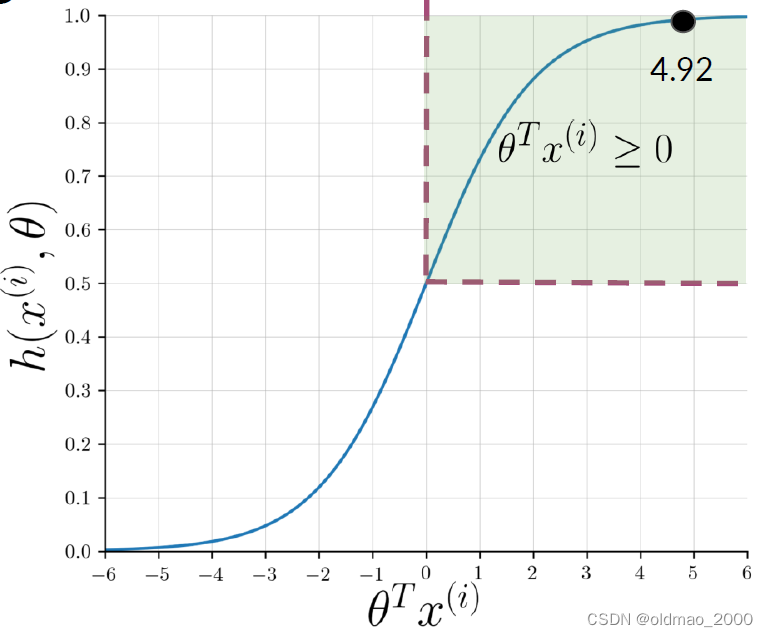
Logistic Regression: Training
上一节内容中,我们使用了给定的参数 θ \theta θ来计算推文的结果,这一节我们将学会如何通过训练逻辑回归模型来找到最佳的参数 θ \theta θ(梯度下降)。
图形化
先将问题简化,假设LR模型中只有两个参数 θ 1 \theta_1 θ1和 θ 2 \theta_2 θ2则函数的参数图像为下左,下右为Cost函数的迭代过程:
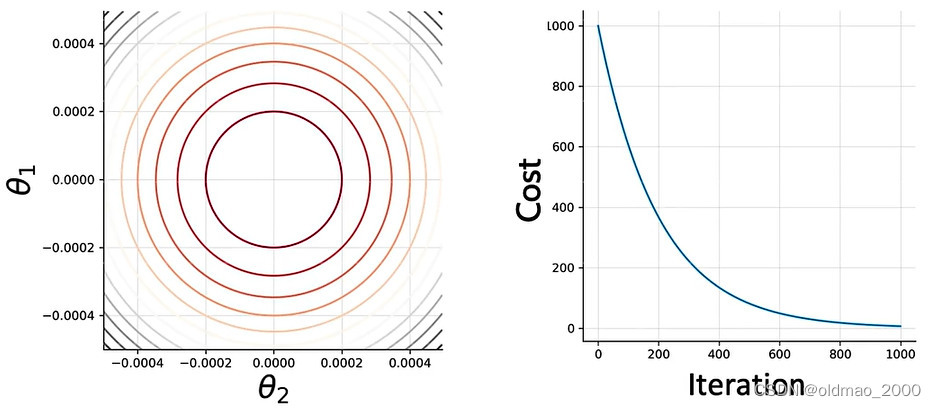
刚开始,我们初始化两个参数 θ 1 \theta_1 θ1和 θ 2 \theta_2 θ2,对应的Cost值为:
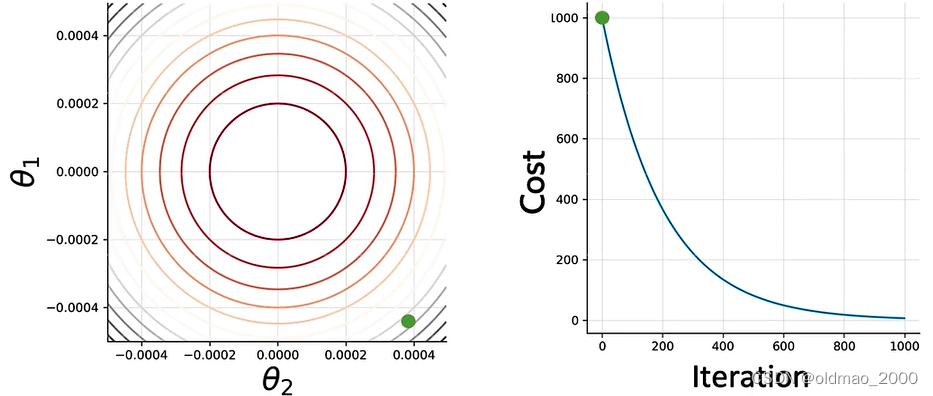
根据GD方向进行参数更新,100次后:
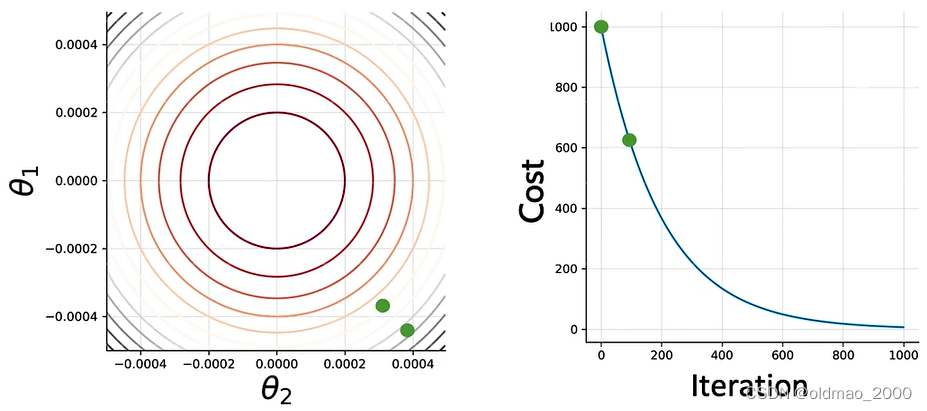
200次后:
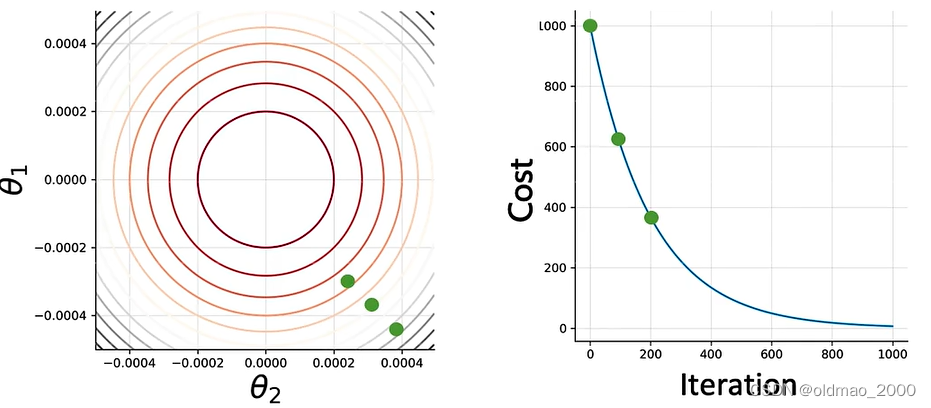
若干次后:
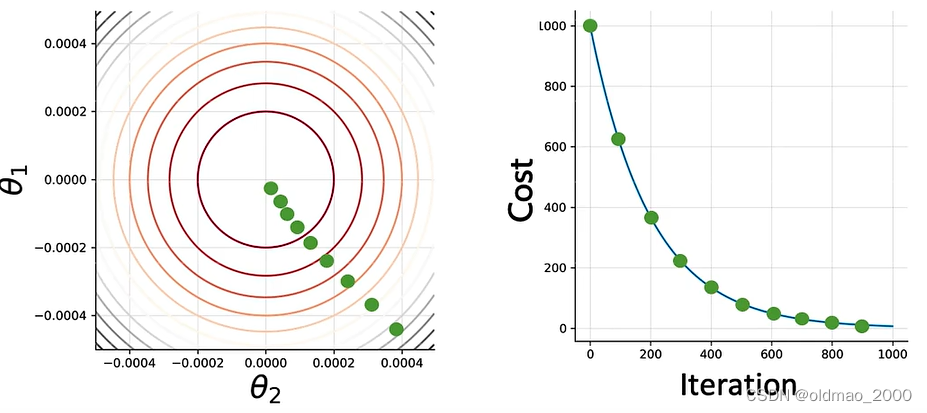
直到最佳cost附近:
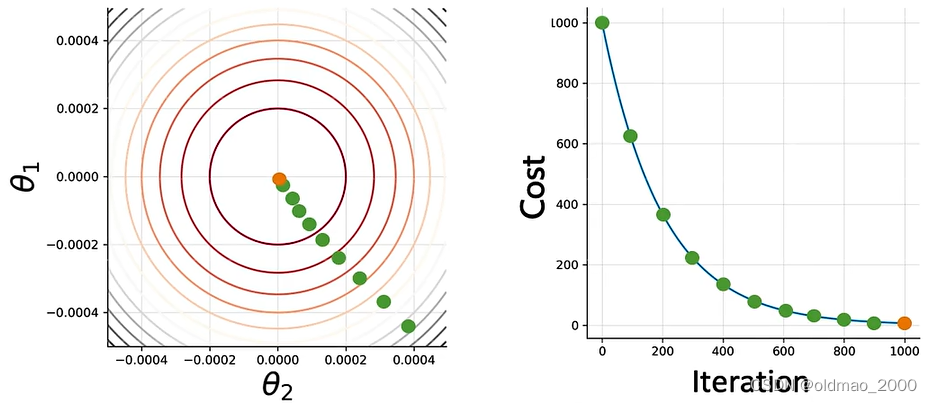
数学化
整个梯度下降过程可以表示为下图,注意左右是一一对应关系,结合起来看:
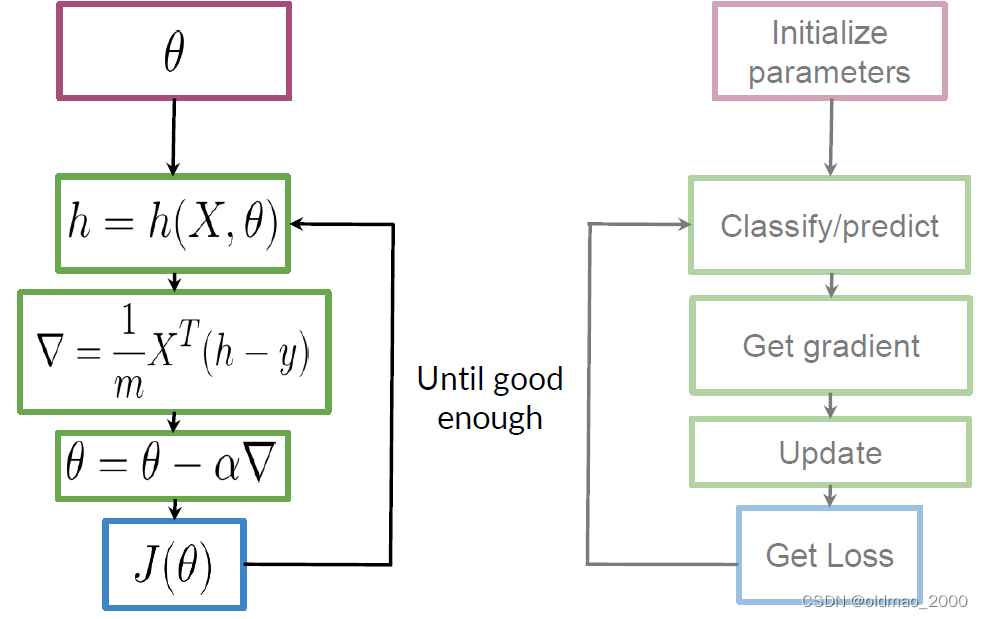
Logistic Regression: Testing
使用验证集计算模型精度,并了解准确度指标的含义。
现在我们手上有验证集: X v a l , Y v a l X_{val},Y_{val} Xval,Yval,以及训练好的参数 θ \theta θ
先计算sigmoid函数值(预测值): h ( X v a l , θ ) h(X_{val},\theta) h(Xval,θ)
然后判断验证集中每一个数据的预测值是否大于阈值(通常为0.5):
p r e d = h ( X v a l , θ ) ≥ 0.5 pred=h(X_{val},\theta)\ge 0.5 pred=h(Xval,θ)≥0.5
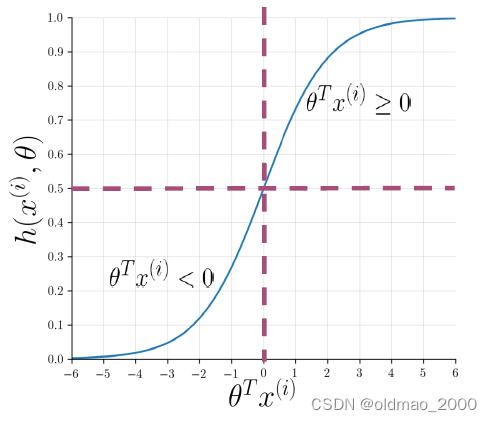
最后的预测结果是一组矩阵:
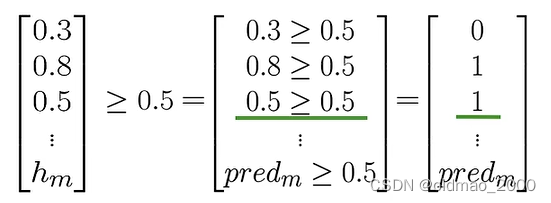
有了预测结果,就可以将其与标签 Y v a l Y_{val} Yval比较,计算准确率:
∑ i = 1 m ( p r e d i = = y v a l ( i ) ) m \sum_{i=1}^m\cfrac{(pred^{i}==y^{(i)}_{val})}{m} i=1∑mm(predi==yval(i))
m是验证集中数据个数
分子如下图所示,绿色是预测正确,黄色是预测不正确的:
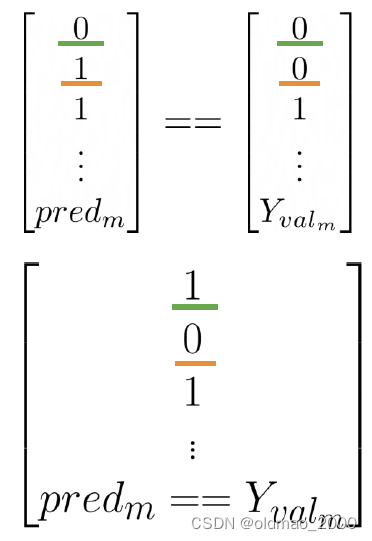
正确率计算实例:
假设计算的预测值与标签如下:
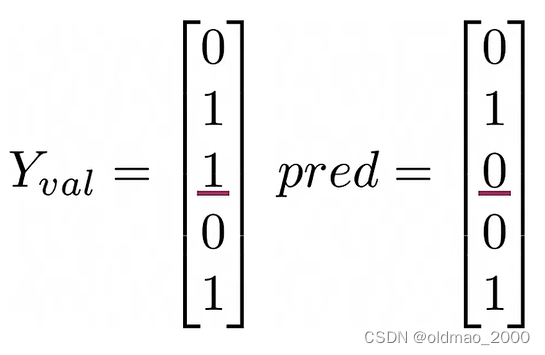
分子则为:
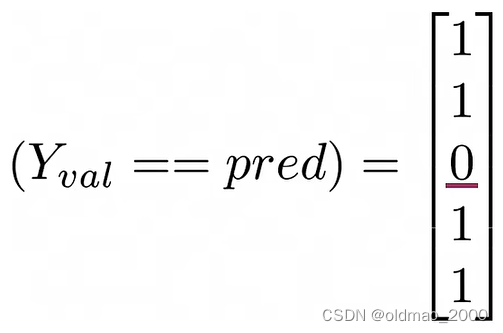
正确率: a c c u r a c y = 4 5 accuracy=\cfrac{4}{5} accuracy=54
opt. Logistic Regression:Cost Function
可选看内容:逻辑成本函数(又称二元交叉熵函数),公式为:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log h ( x ( i ) , θ ) + ( 1 − y ( i ) ) log ( 1 − h ( x ( i ) , θ ) ] J(\theta)=-\cfrac{1}{m}\sum_{i=1}^m\left[y^{(i)}\log h(x^{(i)},\theta)+(1-y^{(i)})\log (1-h(x^{(i)},\theta)\right] J(θ)=−m1i=1∑m[y(i)logh(x(i),θ)+(1−y(i))log(1−h(x(i),θ)]
1 m ∑ i = 1 m \cfrac{1}{m}\sum_{i=1}^m m1∑i=1m中,m是样本数量,这里是将所有训练样本的cost进行累加,然后求平均。
对于中括号的第一项 y ( i ) log h ( x ( i ) , θ ) y^{(i)}\log h(x^{(i)},\theta) y(i)logh(x(i),θ),不同取值有不同结果,总体而言,负例样本 y ( i ) = 0 y^{(i)}=0 y(i)=0,无论预测值 h ( x ( i ) , θ ) h(x^{(i)},\theta) h(x(i),θ)是什么这项为0,而预测值与标签值相差越大,Cost越大:
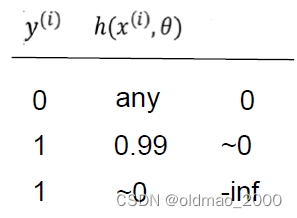
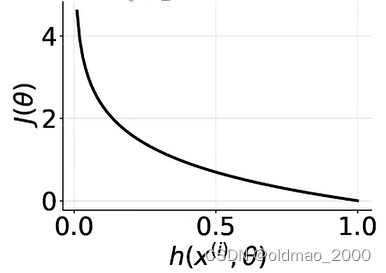
对于中括号的第二项 ( 1 − y ( i ) ) log ( 1 − h ( x ( i ) , θ ) (1-y^{(i)})\log (1-h(x^{(i)},\theta) (1−y(i))log(1−h(x(i),θ),正例样本 y ( i ) = 1 y^{(i)}=1 y(i)=1,无论预测值 h ( x ( i ) , θ ) h(x^{(i)},\theta) h(x(i),θ)是什么这项为0,同样预测值与标签值相差越大,Cost越大:
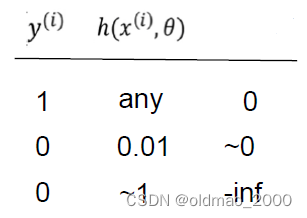
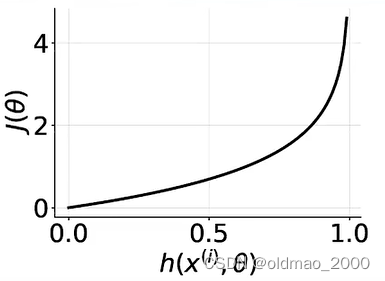
由于中括号里面的log是针对0-1之间的值,所以得到的结果是负数,为保证Cost函数是正值(这样才能求最小),在最前面加上了负号。
作业注意事项
nltk.download(‘twitter_samples’)失败可以到:
https://www.nltk.org/nltk_data/
手工下载twitter_samples.zip后放corpora目录,不用解压
utils.py文件可以在Assignment中找到
